Orientation Entanglement on:
[Wikipedia]
[Google]
[Amazon]
 In
In
 Consider the following example. A coffee cup is suspended in a room by a pair of elastic rubber bands fixed to the walls of the room. The cup is rotated by its handle through a full twist of 360°, so that the handle is brought all the way around the central vertical axis of the cup and back to its original position.
Note that after this rotation, the cup has been returned to its original orientation, but that its orientation with respect to the walls is ''twisted''. In other words, if we lower the coffee cup to the floor of the room, the two bands will coil around each other in one full twist of a
Consider the following example. A coffee cup is suspended in a room by a pair of elastic rubber bands fixed to the walls of the room. The cup is rotated by its handle through a full twist of 360°, so that the handle is brought all the way around the central vertical axis of the cup and back to its original position.
Note that after this rotation, the cup has been returned to its original orientation, but that its orientation with respect to the walls is ''twisted''. In other words, if we lower the coffee cup to the floor of the room, the two bands will coil around each other in one full twist of a  Clearly the geometry of spatial vectors alone is insufficient to express the orientation entanglement (the twist of the rubber bands). Consider drawing a vector across the cup. A full rotation will move the vector around so that the new orientation of the vector is the same as the old one. The vector alone doesn't know that the coffee cup is entangled with the walls of the room.
In fact, the coffee cup is inextricably entangled. There is no way to untwist the bands without rotating the cup. However, consider what happens instead when the cup is rotated, not through just one 360° turn, but ''two'' 360° turns for a total rotation of 720°. Then if the cup is lowered to the floor, the two rubber bands coil around each other in two full twists of a double helix. If the cup is now brought up through the center of one coil of this helix, and passed onto its other side, the twist disappears. The bands are no longer coiled about each other, even though no additional rotation had to be performed. (This experiment is more easily performed with a ribbon or belt. See below.)
Clearly the geometry of spatial vectors alone is insufficient to express the orientation entanglement (the twist of the rubber bands). Consider drawing a vector across the cup. A full rotation will move the vector around so that the new orientation of the vector is the same as the old one. The vector alone doesn't know that the coffee cup is entangled with the walls of the room.
In fact, the coffee cup is inextricably entangled. There is no way to untwist the bands without rotating the cup. However, consider what happens instead when the cup is rotated, not through just one 360° turn, but ''two'' 360° turns for a total rotation of 720°. Then if the cup is lowered to the floor, the two rubber bands coil around each other in two full twists of a double helix. If the cup is now brought up through the center of one coil of this helix, and passed onto its other side, the twist disappears. The bands are no longer coiled about each other, even though no additional rotation had to be performed. (This experiment is more easily performed with a ribbon or belt. See below.)
 Thus, whereas the orientation of the cup was twisted with respect to the walls after a rotation of only 360°, it was no longer twisted after a rotation of 720°. By only considering the vector attached to the cup, it is impossible to distinguish between these two cases, however. It is only when we attach a spinor to the cup that we can distinguish between the twisted and untwisted case.
Thus, whereas the orientation of the cup was twisted with respect to the walls after a rotation of only 360°, it was no longer twisted after a rotation of 720°. By only considering the vector attached to the cup, it is impossible to distinguish between these two cases, however. It is only when we attach a spinor to the cup that we can distinguish between the twisted and untwisted case.
 In this situation, a spinor is a sort of ''polarized'' vector. In the adjacent diagram, a spinor can be represented as a vector whose head is a flag lying on one side of a
In this situation, a spinor is a sort of ''polarized'' vector. In the adjacent diagram, a spinor can be represented as a vector whose head is a flag lying on one side of a
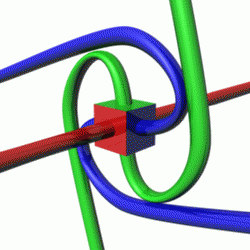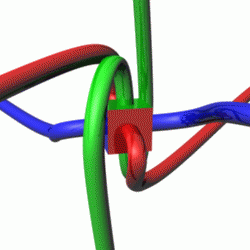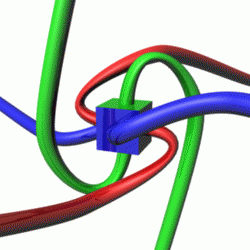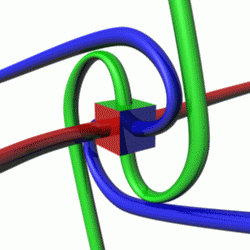
Animation of the Dirac belt trick with two belt attached to a (square) object, showing orientation entanglement after one turn, and lack of entanglement after two turns. The animation thus also shows that belted objects behave as spin 1/2 particles.
Spinors Topology of Lie groups
 In
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
and physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
, the notion of orientation entanglement is sometimes used to develop intuition relating to the geometry of spinors
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight ...
or alternatively as a concrete realization of the failure of the special orthogonal group
In mathematics, the orthogonal group in dimension , denoted , is the group of distance-preserving transformations of a Euclidean space of dimension that preserve a fixed point, where the group operation is given by composing transformations. T ...
s to be simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the spac ...
.
Elementary description
Spatial vectors alone are not sufficient to describe fully the properties of rotations in space. Consider the following example. A coffee cup is suspended in a room by a pair of elastic rubber bands fixed to the walls of the room. The cup is rotated by its handle through a full twist of 360°, so that the handle is brought all the way around the central vertical axis of the cup and back to its original position.
Note that after this rotation, the cup has been returned to its original orientation, but that its orientation with respect to the walls is ''twisted''. In other words, if we lower the coffee cup to the floor of the room, the two bands will coil around each other in one full twist of a
Consider the following example. A coffee cup is suspended in a room by a pair of elastic rubber bands fixed to the walls of the room. The cup is rotated by its handle through a full twist of 360°, so that the handle is brought all the way around the central vertical axis of the cup and back to its original position.
Note that after this rotation, the cup has been returned to its original orientation, but that its orientation with respect to the walls is ''twisted''. In other words, if we lower the coffee cup to the floor of the room, the two bands will coil around each other in one full twist of a double helix
A double is a look-alike or doppelgänger; one person or being that resembles another.
Double, The Double or Dubble may also refer to:
Film and television
* Double (filmmaking), someone who substitutes for the credited actor of a character
* ...
. This is an example of orientation entanglement: the new orientation of the coffee cup embedded in the room is not actually the same as the old orientation, as evidenced by the twisting of the rubber bands. Stated another way, the orientation of the coffee cup has become entangled with the orientation of the surrounding walls.
 Thus, whereas the orientation of the cup was twisted with respect to the walls after a rotation of only 360°, it was no longer twisted after a rotation of 720°. By only considering the vector attached to the cup, it is impossible to distinguish between these two cases, however. It is only when we attach a spinor to the cup that we can distinguish between the twisted and untwisted case.
Thus, whereas the orientation of the cup was twisted with respect to the walls after a rotation of only 360°, it was no longer twisted after a rotation of 720°. By only considering the vector attached to the cup, it is impossible to distinguish between these two cases, however. It is only when we attach a spinor to the cup that we can distinguish between the twisted and untwisted case.
 In this situation, a spinor is a sort of ''polarized'' vector. In the adjacent diagram, a spinor can be represented as a vector whose head is a flag lying on one side of a
In this situation, a spinor is a sort of ''polarized'' vector. In the adjacent diagram, a spinor can be represented as a vector whose head is a flag lying on one side of a Möbius strip
In mathematics, a Möbius strip, Möbius band, or Möbius loop is a surface that can be formed by attaching the ends of a strip of paper together with a half-twist. As a mathematical object, it was discovered by Johann Benedict Listing and Augu ...
, pointing inward. Initially, suppose that the flag is on top of the strip as shown. As the coffee cup is rotated it carries the spinor, and its flag, along the strip. If the cup is rotated through 360°, the spinor returns to the initial position, but the flag is now underneath the strip, pointing outward. It takes another 360° rotation in order to return the flag to its original orientation.
A detailed bridge between the above, and the formal mathematics can be found in the article on tangloids
Tangloids is a mathematical game for two players created by Piet Hein to model the calculus of spinors.
A description of the game appeared in the book ''"Martin Gardner's New Mathematical Diversions from Scientific American"'' by Martin Gardner ...
.
Formal details
In three dimensions, the problem illustrated above corresponds to the fact that theLie group
In mathematics, a Lie group (pronounced ) is a group that is also a differentiable manifold. A manifold is a space that locally resembles Euclidean space, whereas groups define the abstract concept of a binary operation along with the additio ...
SO(3)
In mechanics and geometry, the 3D rotation group, often denoted SO(3), is the group of all rotations about the origin of three-dimensional Euclidean space \R^3 under the operation of composition.
By definition, a rotation about the origin is a tr ...
is not simply connected
In topology, a topological space is called simply connected (or 1-connected, or 1-simply connected) if it is path-connected and every path between two points can be continuously transformed (intuitively for embedded spaces, staying within the spac ...
. Mathematically, one can tackle this problem by exhibiting the special unitary group
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1.
The more general unitary matrices may have complex determinants with absolute value 1, rather than real 1 in the special ...
, SU(2)
In mathematics, the special unitary group of degree , denoted , is the Lie group of unitary matrices with determinant 1.
The more general unitary matrices may have complex determinants with absolute value 1, rather than real 1 in the special ...
, which is also the spin group
In mathematics the spin group Spin(''n'') page 15 is the double cover of the special orthogonal group , such that there exists a short exact sequence of Lie groups (when )
:1 \to \mathrm_2 \to \operatorname(n) \to \operatorname(n) \to 1.
As a L ...
in three Euclidean dimensions, as a double cover of SO(3). If is a vector in R3, then we identify ''X'' with the 2 × 2 matrix with complex entries
:
Note that −det(''X'') gives the square of the Euclidean length of ''X'' regarded as a vector, and that ''X'' is a trace-free
In linear algebra, the trace of a square matrix , denoted , is defined to be the sum of elements on the main diagonal (from the upper left to the lower right) of . The trace is only defined for a square matrix ().
It can be proved that the trace o ...
, or better, trace-zero Hermitian matrix
In mathematics, a Hermitian matrix (or self-adjoint matrix) is a complex square matrix that is equal to its own conjugate transpose—that is, the element in the -th row and -th column is equal to the complex conjugate of the element in the -th ...
.
The unitary group acts on ''X'' via
:
where ''M'' ∈ SU(2). Note that, since ''M'' is unitary,
:, and
: is trace-zero Hermitian.
Hence SU(2) acts via rotation on the vectors ''X''. Conversely, since any change of basis
In mathematics, an ordered basis of a vector space of finite dimension allows representing uniquely any element of the vector space by a coordinate vector, which is a sequence of scalars called coordinates. If two different bases are considere ...
which sends trace-zero Hermitian matrices to trace-zero Hermitian matrices must be unitary, it follows that every rotation also lifts to SU(2). However, each rotation is obtained from a pair of elements ''M'' and −''M'' of SU(2). Hence SU(2) is a double-cover of SO(3). Furthermore, SU(2) is easily seen to be itself simply connected by realizing it as the group of unit quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. Hamilton defined a quatern ...
s, a space homeomorphic
In the mathematical field of topology, a homeomorphism, topological isomorphism, or bicontinuous function is a bijective and continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphi ...
to the 3-sphere
In mathematics, a 3-sphere is a higher-dimensional analogue of a sphere. It may be embedded in 4-dimensional Euclidean space as the set of points equidistant from a fixed central point. Analogous to how the boundary of a ball in three dimensi ...
.
A unit quaternion has the cosine of half the rotation angle as its scalar part and the sine of half the rotation angle multiplying a unit vector along some rotation axis (here assumed fixed) as its pseudovector (or axial vector) part. If the initial orientation of a rigid body (with unentangled connections to its fixed surroundings) is identified with a unit quaternion having a zero pseudovector part and +1 for the scalar part, then after one complete rotation (2π rad) the pseudovector part returns to zero and the scalar part has become −1 (entangled). After two complete rotations (4π rad) the pseudovector part again returns to zero and the scalar part returns to +1 (unentangled), completing the cycle.
See also
*Plate trick
In mathematics and physics, the plate trick, also known as Dirac's string trick, the belt trick, or the Balinese cup trick, is any of several demonstrations of the idea that rotating an object with strings attached to it by 360 degrees does not r ...
* Tangloids
Tangloids is a mathematical game for two players created by Piet Hein to model the calculus of spinors.
A description of the game appeared in the book ''"Martin Gardner's New Mathematical Diversions from Scientific American"'' by Martin Gardner ...
Notes
References
*Feynman, Leighton, Sands.The Feynman Lectures on Physics
''The Feynman Lectures on Physics'' is a physics textbook based on some lectures by Richard Feynman, a Nobel laureate who has sometimes been called "The Great Explainer". The lectures were presented before undergraduate students at the Californ ...
. 3 volumes 1964, 1966. Library of Congress Catalog Card No. 63-20717
*:* (1970 paperback three-volume set)
*:* (1989 commemorative hardcover three-volume set)
*:* {{ISBN, 0-8053-9045-6 (2006 the definitive edition (2nd printing); hardcover)
External links
Animation of the Dirac belt trick with two belt attached to a (square) object, showing orientation entanglement after one turn, and lack of entanglement after two turns. The animation thus also shows that belted objects behave as spin 1/2 particles.
Spinors Topology of Lie groups