Newton–Gauss Line on:
[Wikipedia]
[Google]
[Amazon]
 In geometry, the Newton–Gauss line (or Gauss–Newton line) is the
In geometry, the Newton–Gauss line (or Gauss–Newton line) is the
 It is a well-known theorem that the three midpoints of the diagonals of a complete quadrilateral are collinear.
There are several proofs of the result based on areas or wedge products or, as the following proof, on Menelaus's theorem, due to Hillyer and published in 1920.
Let the complete quadrilateral be labeled as in the diagram with diagonals and their respective midpoints . Let the midpoints of be respectively. Using similar triangles it is seen that intersects at , intersects at and intersects at . Again, similar triangles provide the following proportions,
:
However, the line intersects the sides of triangle , so by Menelaus's theorem the product of the terms on the right hand sides is −1. Thus, the product of the terms on the left hand sides is also −1 and again by Menelaus's theorem, the points are collinear on the sides of triangle .
It is a well-known theorem that the three midpoints of the diagonals of a complete quadrilateral are collinear.
There are several proofs of the result based on areas or wedge products or, as the following proof, on Menelaus's theorem, due to Hillyer and published in 1920.
Let the complete quadrilateral be labeled as in the diagram with diagonals and their respective midpoints . Let the midpoints of be respectively. Using similar triangles it is seen that intersects at , intersects at and intersects at . Again, similar triangles provide the following proportions,
:
However, the line intersects the sides of triangle , so by Menelaus's theorem the product of the terms on the right hand sides is −1. Thus, the product of the terms on the left hand sides is also −1 and again by Menelaus's theorem, the points are collinear on the sides of triangle .
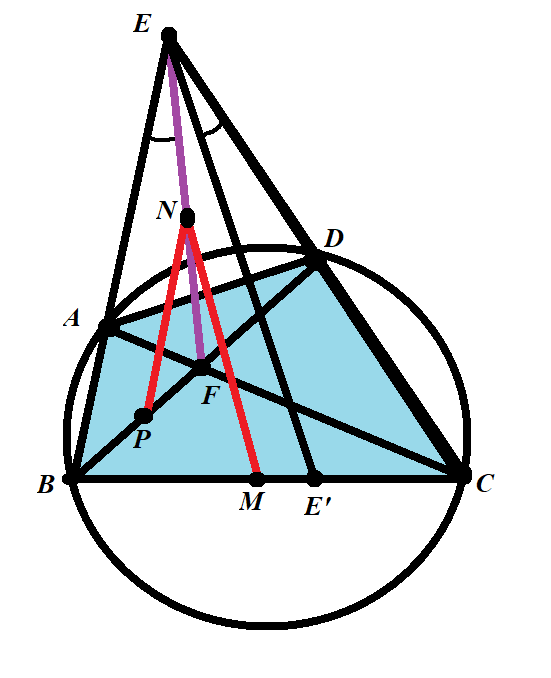
 Given any cyclic quadrilateral , let point be the point of intersection between the two diagonals and . Extend the diagonals and until they meet at the point of intersection, . Let the midpoint of the segment be , and let the midpoint of the segment be (Figure 1).
Given any cyclic quadrilateral , let point be the point of intersection between the two diagonals and . Extend the diagonals and until they meet at the point of intersection, . Let the midpoint of the segment be , and let the midpoint of the segment be (Figure 1).


 In geometry, the Newton–Gauss line (or Gauss–Newton line) is the
In geometry, the Newton–Gauss line (or Gauss–Newton line) is the line
Line most often refers to:
* Line (geometry), object with zero thickness and curvature that stretches to infinity
* Telephone line, a single-user circuit on a telephone communication system
Line, lines, The Line, or LINE may also refer to:
Arts ...
joining the midpoints of the three diagonals of a complete quadrilateral.
The midpoints of the two diagonals of a convex quadrilateral with at most two parallel sides are distinct and thus determine a line, the Newton line. If the sides of such a quadrilateral are extended to form a complete quadrangle, the diagonals of the quadrilateral remain diagonals of the complete quadrangle and the Newton line of the quadrilateral is the Newton–Gauss line of the complete quadrangle.
Complete quadrilaterals
Any four lines in general position (no two lines are parallel, and no three are concurrent) form a complete quadrilateral. Thisconfiguration
Configuration or configurations may refer to:
Computing
* Computer configuration or system configuration
* Configuration file, a software file used to configure the initial settings for a computer program
* Configurator, also known as choice board ...
consists of a total of six points, the intersection points of the four lines, with three points on each line and precisely two lines through each point. These six points can be split into pairs so that the line segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
s determined by any pair do not intersect any of the given four lines except at the endpoints. These three line segments are called diagonals of the complete quadrilateral.
Existence of the Newton−Gauss line
Applications to cyclic quadrilaterals
The following are some results that use the Newton–Gauss line of complete quadrilaterals that are associated with cyclic quadrilaterals, based on the work of Barbu and Patrascu.Equal angles
 Given any cyclic quadrilateral , let point be the point of intersection between the two diagonals and . Extend the diagonals and until they meet at the point of intersection, . Let the midpoint of the segment be , and let the midpoint of the segment be (Figure 1).
Given any cyclic quadrilateral , let point be the point of intersection between the two diagonals and . Extend the diagonals and until they meet at the point of intersection, . Let the midpoint of the segment be , and let the midpoint of the segment be (Figure 1).
Theorem
If the midpoint of the line segment is , the Newton–Gauss line of the complete quadrilateral and the line determine an angle equal to .= Proof
= First show that the triangles are similar. Since and , we know . Also, In the cyclic quadrilateral , theseequalities
In mathematics, equality is a relationship between two quantities or, more generally two mathematical expressions, asserting that the quantities have the same value, or that the expressions represent the same mathematical object. The equality b ...
hold:
:
Therefore, .
Let be the radii of the circumcircles of respectively. Apply the law of sines to the triangles, to obtain:
:
Since and , this shows the equality The similarity of triangles follows, and .
= Remark
= If is the midpoint of the line segment , it follows by the same reasoning that .
Isogonal lines
Theorem
The line through parallel to the Newton–Gauss line of the complete quadrilateral and the line are isogonal lines of , that is, each line is a reflection of the other about the angle bisector. (Figure 2)= Proof
= Triangles are similar by the above argument, so . Let be the point of intersection of and the line parallel to the Newton–Gauss line through . Since and , and . Therefore, :Two cyclic quadrilaterals sharing a Newton-Gauss line

Lemma
Let and be theorthogonal projections
In linear algebra and functional analysis, a projection is a linear transformation P from a vector space to itself (an endomorphism) such that P\circ P=P. That is, whenever P is applied twice to any vector, it gives the same result as if it wer ...
of the point on the lines and respectively.
The quadrilaterals and are cyclic quadrilaterals.
= Proof
= , as previously shown. The points and are the respective circumcenters of the right triangles . Thus, and . Therefore, : Therefore, is a cyclic quadrilateral, and by the same reasoning, also lies on a circle.
Theorem
Extend the lines to intersect at respectively (Figure 4). The complete quadrilaterals and have the same Newton–Gauss line.= Proof
= The two complete quadrilaterals have a shared diagonal, . lies on the Newton–Gauss line of both quadrilaterals. is equidistant from and , since it is the circumcenter of the cyclic quadrilateral . If triangles are congruent, and it will follow that lies on the perpendicular bisector of the line . Therefore, the line contains the midpoint of , and is the Newton–Gauss line of . To show that the triangles are congruent, first observe that is aparallelogram
In Euclidean geometry, a parallelogram is a simple (non- self-intersecting) quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equa ...
, since the points are midpoints of respectively.
Therefore,
:
Also note that
:
Hence,
:
Therefore, and are congruent by SAS.
= Remark
= Due to being congruent triangles, their circumcircles are also congruent.History
The Newton–Gauss line proof was developed by the two mathematicians it is named after: Sir Isaac Newton and Carl Friedrich Gauss. The initial framework for this theorem is from the work ofNewton
Newton most commonly refers to:
* Isaac Newton (1642–1726/1727), English scientist
* Newton (unit), SI unit of force named after Isaac Newton
Newton may also refer to:
Arts and entertainment
* ''Newton'' (film), a 2017 Indian film
* Newton ( ...
, in his previous theorem on the Newton line, in which Newton showed that the center of a conic inscribed in a quadrilateral lies on the Newton–Gauss line.
The theorem of Gauss and Bodenmiller states that the three circles whose diameters are the diagonals of a complete quadrilateral are coaxal.
Notes
References
* **(available on-line as)External links
* {{DEFAULTSORT:Newton-Gauss line Geometry Quadrilaterals