Multiplication on:
[Wikipedia]
[Google]
[Amazon]

 Multiplication is one of the four elementary mathematical operations of
Multiplication is one of the four elementary mathematical operations of
 The product of two natural numbers is defined as:
The product of two natural numbers is defined as:
 The geometric meaning of complex multiplication can be understood by rewriting complex numbers in
The geometric meaning of complex multiplication can be understood by rewriting complex numbers in
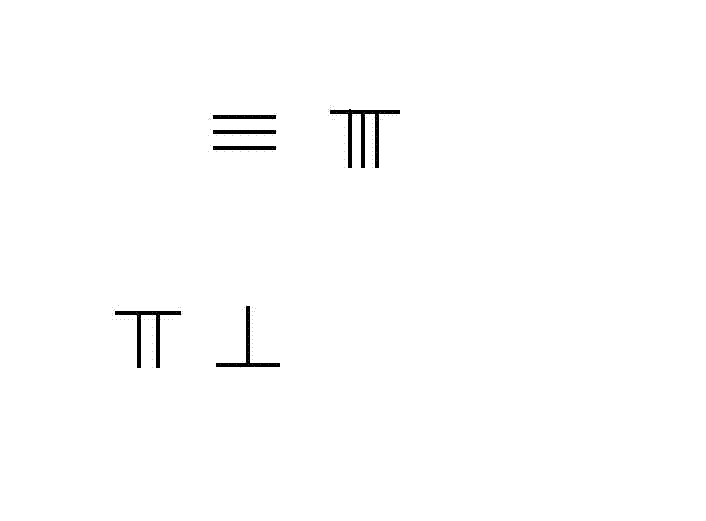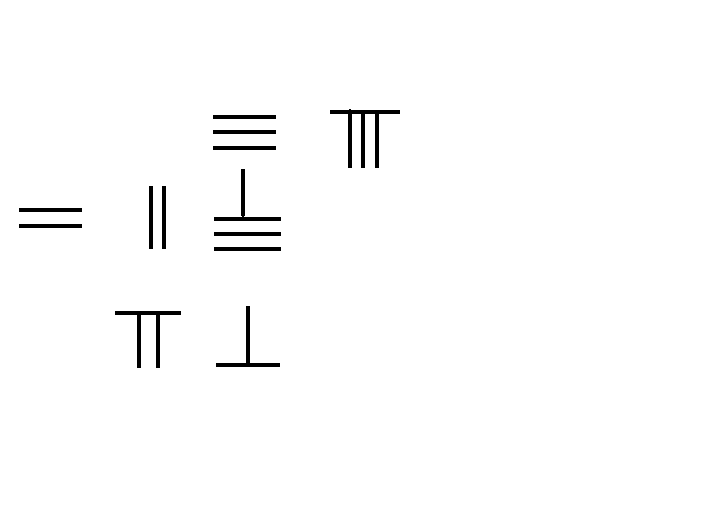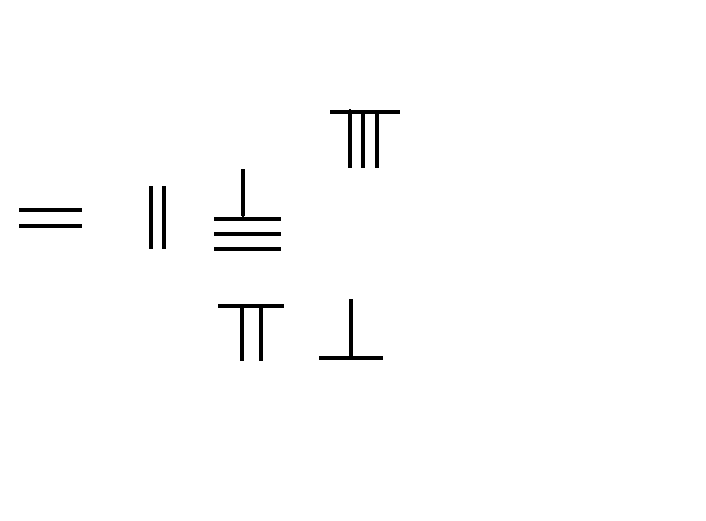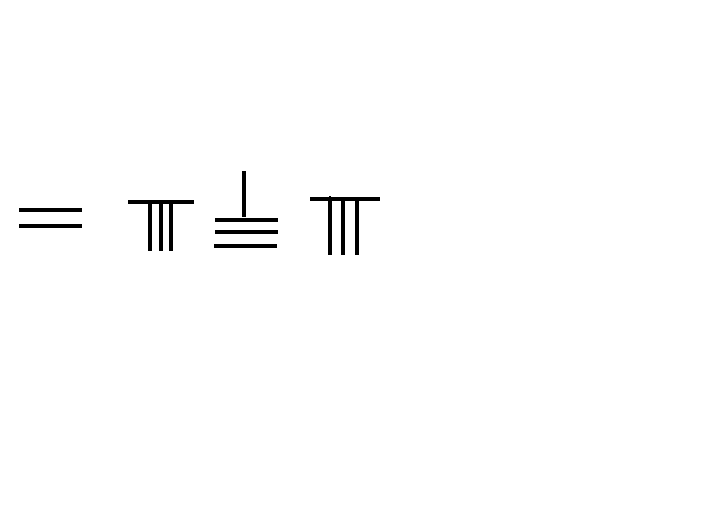 In the mathematical text '' Zhoubi Suanjing'', dated prior to 300 BC, and the ''
In the mathematical text '' Zhoubi Suanjing'', dated prior to 300 BC, and the ''
Multiplication
an
Arithmetic Operations In Various Number Systems
at
Modern Chinese Multiplication Techniques on an Abacus
{{Authority control Elementary arithmetic Mathematical notation Articles containing proofs
arithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
, with the other ones being addition
Addition (usually signified by the Plus and minus signs#Plus sign, plus symbol, +) is one of the four basic Operation (mathematics), operations of arithmetic, the other three being subtraction, multiplication, and Division (mathematics), divis ...
, subtraction
Subtraction (which is signified by the minus sign, –) is one of the four Arithmetic#Arithmetic operations, arithmetic operations along with addition, multiplication and Division (mathematics), division. Subtraction is an operation that repre ...
, and division. The result of a multiplication operation is called a '' product''. Multiplication is often denoted by the cross symbol, , by the mid-line dot operator, , by juxtaposition, or, in programming languages, by an asterisk, .
The multiplication of whole numbers may be thought of as repeated addition; that is, the multiplication of two numbers is equivalent to adding as many copies of one of them, the ''multiplicand'', as the quantity of the other one, the ''multiplier''; both numbers can be referred to as ''factors''. This is to be distinguished from ''terms'', which are added.
:
Whether the first factor is the multiplier or the multiplicand may be ambiguous or depend upon context. For example, the expression , can be phrased as "3 times 4" and evaluated as , where 3 is the multiplier, but also as "3 multiplied by 4", in which case 3 becomes the multiplicand. One of the main properties of multiplication is the commutative property, which states in this case that adding 3 copies of 4 gives the same result as adding 4 copies of 3. Thus, the designation of multiplier and multiplicand does not affect the result of the multiplication.
Systematic generalizations of this basic definition define the multiplication of integers (including negative numbers), rational numbers (fractions), and real numbers.
Multiplication can also be visualized as counting objects arranged in a rectangle (for whole numbers) or as finding the area of a rectangle whose sides have some given lengths. The area of a rectangle does not depend on which side is measured first—a consequence of the commutative property.
The product of two measurements (or physical quantities
A physical quantity (or simply quantity) is a property of a material or system that can be quantified by measurement. A physical quantity can be expressed as a ''value'', which is the algebraic multiplication of a '' numerical value'' and a '' ...
) is a new type of measurement (or new quantity), usually with a derived unit of measurement
A unit of measurement, or unit of measure, is a definite magnitude (mathematics), magnitude of a quantity, defined and adopted by convention or by law, that is used as a standard for measurement of the same kind of quantity. Any other qua ...
. For example, multiplying the lengths (in meters or feet) of the two sides of a rectangle gives its area (in square meters or square feet). Such a product is the subject of dimensional analysis.
The inverse operation of multiplication is '' division''. For example, since 4 multiplied by 3 equals 12, 12 divided by 3 equals 4. Indeed, multiplication by 3, followed by division by 3, yields the original number. The division of a number other than 0 by itself equals 1.
Several mathematical concepts expand upon the fundamental idea of multiplication. The product of a sequence, vector multiplication, complex numbers, and matrices are all examples where this can be seen. These more advanced constructs tend to affect the basic properties in their own ways, such as becoming noncommutative in matrices and some forms of vector multiplication or changing the sign of complex numbers.
Notation
Inarithmetic
Arithmetic is an elementary branch of mathematics that deals with numerical operations like addition, subtraction, multiplication, and division. In a wider sense, it also includes exponentiation, extraction of roots, and taking logarithms.
...
, multiplication is often written using the multiplication sign
The multiplication sign (), also known as the times sign or the dimension sign, is a mathematical symbol used to denote the operation of multiplication, which results in a product.
The symbol is also used in botany, in botanical hybrid nam ...
(either or ) between the factors (that is, in infix notation
Infix notation is the notation commonly used in arithmetical and logical formulae and statements. It is characterized by the placement of operators between operands—"infixed operators"—such as the plus sign in .
Usage
Binary relations are ...
). For example,
: ("two times three equals six")
:
:
:
There are other mathematical notation
Mathematical notation consists of using glossary of mathematical symbols, symbols for representing operation (mathematics), operations, unspecified numbers, relation (mathematics), relations, and any other mathematical objects and assembling ...
s for multiplication:
* To reduce confusion between the multiplication sign × and the common variable , multiplication is also denoted by dot signs, usually a middle-position dot (rarely period): . The middle dot notation or dot operator is now standard in the United States and other countries. When the dot operator character is not accessible, the interpunct
An interpunct , also known as an interpoint, middle dot, middot, centered dot or centred dot, is a punctuation mark consisting of a vertically centered dot used for interword separation in Classical Latin. ( Word-separating spaces did not appe ...
() is used. In most European and other countries that use a comma
The comma is a punctuation mark that appears in several variants in different languages. Some typefaces render it as a small line, slightly curved or straight, but inclined from the vertical; others give it the appearance of a miniature fille ...
as a decimal point
FIle:Decimal separators.svg, alt=Four types of separating decimals: a) 1,234.56. b) 1.234,56. c) 1'234,56. d) ١٬٢٣٤٫٥٦., Both a comma and a full stop (or period) are generally accepted decimal separators for international use. The apost ...
(and a period as a thousands separator
alt=Four types of separating decimals: a) 1,234.56. b) 1.234,56. c) 1'234,56. d) ١٬٢٣٤٫٥٦., Both a full_stop.html" ;"title="comma and a full stop">comma and a full stop (or period) are generally accepted decimal separators for interna ...
), the multiplication sign or a middle dot is used to indicate multiplication. Historically, in the United Kingdom and Ireland, the middle dot was sometimes used for the decimal point to prevent it from disappearing in the ruled line, and the full stop (period) was used for multiplication. However, since the Ministry of Technology
The Ministry of Technology was a department of the government of the United Kingdom, sometimes abbreviated as "MinTech". The Ministry of Technology was established by the incoming government of Harold Wilson in October 1964 as part of Wilson's am ...
ruled in 1968 that the period be used as the decimal point, and the International System of Units
The International System of Units, internationally known by the abbreviation SI (from French ), is the modern form of the metric system and the world's most widely used system of measurement. It is the only system of measurement with official s ...
(SI) standard has since been widely adopted, this usage is now found only in the more traditional journals such as ''The Lancet
''The Lancet'' is a weekly peer-reviewed general medical journal, founded in England in 1823. It is one of the world's highest-impact academic journals and also one of the oldest medical journals still in publication.
The journal publishes ...
''.
* In algebra
Algebra is a branch of mathematics that deals with abstract systems, known as algebraic structures, and the manipulation of expressions within those systems. It is a generalization of arithmetic that introduces variables and algebraic ope ...
, multiplication involving variables is often written as a juxtaposition
Juxtaposition is an act or instance of placing two opposing elements close together or side by side. This is often done in order to Comparison, compare/contrast the two, to show similarities or differences, etc.
Speech
Juxtaposition in literary ...
(e.g., for times or for five times ), also called implied multiplication. The notation can also be used for quantities that are surrounded by parentheses (e.g., , or for five times two). This implicit usage of multiplication can cause ambiguity when the concatenated variables happen to match the name of another variable, when a variable name in front of a parenthesis can be confused with a function name, or in the correct determination of the order of operations
In mathematics and computer programming, the order of operations is a collection of rules that reflect conventions about which operations to perform first in order to evaluate a given mathematical expression.
These rules are formalized with a ...
.
* In vector multiplication, there is a distinction between the cross and the dot symbols. The cross symbol generally denotes the taking a cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and ...
of two vectors, yielding a vector as its result, while the dot denotes taking the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a Scalar (mathematics), scalar as a result". It is also used for other symmetric bilinear forms, for example in a pseudo-Euclidean space. N ...
of two vectors, resulting in a scalar.
In computer programming
Computer programming or coding is the composition of sequences of instructions, called computer program, programs, that computers can follow to perform tasks. It involves designing and implementing algorithms, step-by-step specifications of proc ...
, the asterisk
The asterisk ( ), from Late Latin , from Ancient Greek , , "little star", is a Typography, typographical symbol. It is so called because it resembles a conventional image of a star (heraldry), heraldic star.
Computer scientists and Mathematici ...
(as in 5*2) is still the most common notation. This is because most computers historically were limited to small character set
Character encoding is the process of assigning numbers to graphical characters, especially the written characters of human language, allowing them to be stored, transmitted, and transformed using computers. The numerical values that make up a c ...
s (such as ASCII
ASCII ( ), an acronym for American Standard Code for Information Interchange, is a character encoding standard for representing a particular set of 95 (English language focused) printable character, printable and 33 control character, control c ...
and EBCDIC
Extended Binary Coded Decimal Interchange Code (EBCDIC; ) is an eight- bit character encoding used mainly on IBM mainframe and IBM midrange computer operating systems. It descended from the code used with punched cards and the corresponding si ...
) that lacked a multiplication sign (such as ⋅ or ×), while the asterisk appeared on every keyboard. This usage originated in the FORTRAN programming language.
The numbers to be multiplied are generally called the "factors" (as in factorization). The number to be multiplied is the "multiplicand", and the number by which it is multiplied is the "multiplier". Usually, the multiplier is placed first, and the multiplicand is placed second; however, sometimes the first factor is considered the multiplicand and the second the multiplier.
Also, as the result of multiplication does not depend on the order of the factors, the distinction between "multiplicand" and "multiplier" is useful only at a very elementary level and in some multiplication algorithms, such as the long multiplication. Therefore, in some sources, the term "multiplicand" is regarded as a synonym for "factor".
In algebra, a number that is the multiplier of a variable or expression (e.g., the 3 in ) is called a coefficient
In mathematics, a coefficient is a Factor (arithmetic), multiplicative factor involved in some Summand, term of a polynomial, a series (mathematics), series, or any other type of expression (mathematics), expression. It may be a Dimensionless qu ...
.
The result of a multiplication is called a product. When one factor is an integer, the product is a ''multiple'' of the other or of the product of the others. Thus, is a multiple of , as is . A product of integers is a multiple of each factor; for example, 15 is the product of 3 and 5 and is both a multiple of 3 and a multiple of 5.
Definitions
The product of two numbers or the multiplication between two numbers can be defined for common special cases: natural numbers, integers, rational numbers, real numbers, complex numbers, and quaternions.Product of two natural numbers
Product of two integers
An integer can be either zero, a nonzero natural number, or minus a nonzero natural number. The product of zero and another integer is always zero. The product of two nonzero integers is determined by the product of their positive amounts, combined with the sign derived from the following rule: (This rule is a consequence of thedistributivity
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary ...
of multiplication over addition, and is not an ''additional rule''.)
In words:
* A positive number multiplied by a positive number is positive (product of natural numbers),
* A positive number multiplied by a negative number is negative,
* A negative number multiplied by a positive number is negative,
* A negative number multiplied by a negative number is positive.
Product of two fractions
Two fractions can be multiplied by multiplying their numerators and denominators: : :which is defined when .Product of two real numbers
There are several equivalent ways to define formally the real numbers; see Construction of the real numbers. The definition of multiplication is a part of all these definitions. A fundamental aspect of these definitions is that every real number can be approximated to any accuracy byrational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
s. A standard way for expressing this is that every real number is the least upper bound of a set of rational numbers. In particular, every positive real number is the least upper bound of the truncations of its infinite decimal representation
A decimal representation of a non-negative real number is its expression as a sequence of symbols consisting of decimal digits traditionally written with a single separator:
r = b_k b_\cdots b_0.a_1a_2\cdots
Here is the decimal separator, ...
; for example, is the least upper bound of
A fundamental property of real numbers is that rational approximations are compatible with arithmetic operations, and, in particular, with multiplication. This means that, if and are positive real numbers such that and then In particular, the product of two positive real numbers is the least upper bound of the term-by-term products of the sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is cal ...
s of their decimal representations.
As changing the signs transforms least upper bounds into greatest lower bounds, the simplest way to deal with a multiplication involving one or two negative numbers, is to use the rule of signs described above in . The construction of the real numbers through Cauchy sequence
In mathematics, a Cauchy sequence is a sequence whose elements become arbitrarily close to each other as the sequence progresses. More precisely, given any small positive distance, all excluding a finite number of elements of the sequence are le ...
s is often preferred in order to avoid consideration of the four possible sign configurations.
Product of two complex numbers
Two complex numbers can be multiplied by the distributive law and the fact that , as follows: :polar coordinates
In mathematics, the polar coordinate system specifies a given point (mathematics), point in a plane (mathematics), plane by using a distance and an angle as its two coordinate system, coordinates. These are
*the point's distance from a reference ...
:
:
Furthermore,
:
from which one obtains
:
The geometric meaning is that the magnitudes are multiplied and the arguments are added.
Product of two quaternions
The product of twoquaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s can be found in the article on quaternions. Note, in this case, that and are in general different.
Computation
upThe Educated Monkey—a For example: set the monkey's feet to 4 and 9, and get the product—36—in its hands.">tin toy dated 1918, used as a multiplication "calculator". For example: set the monkey's feet to 4 and 9, and get the product—36—in its hands. Many common methods for multiplying numbers using pencil and paper require a multiplication table of memorized or consulted products of small numbers (typically any two numbers from 0 to 9). However, one method, the peasant multiplication algorithm, does not. The example below illustrates "long multiplication" (the "standard algorithm", "grade-school multiplication"): 23958233 × 5830 ——————————————— 00000000 ( = 23,958,233 × 0) 71874699 ( = 23,958,233 × 30) 191665864 ( = 23,958,233 × 800) + 119791165 ( = 23,958,233 × 5,000) ——————————————— 139676498390 ( = 139,676,498,390 ) In some countries such asGermany
Germany, officially the Federal Republic of Germany, is a country in Central Europe. It lies between the Baltic Sea and the North Sea to the north and the Alps to the south. Its sixteen States of Germany, constituent states have a total popu ...
, the multiplication above is depicted similarly but with the original problem written on a single line and computation starting with the first digit of the multiplier:
23958233 · 5830
———————————————
119791165
191665864
71874699
00000000
———————————————
139676498390
Multiplying numbers to more than a couple of decimal places by hand is tedious and error-prone. Common logarithms were invented to simplify such calculations, since adding logarithms is equivalent to multiplying. The slide rule allowed numbers to be quickly multiplied to about three places of accuracy. Beginning in the early 20th century, mechanical calculator
An electronic calculator is typically a portable electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics.
The first solid-state electronic calculator was created in the early 1960s. Pocket-si ...
s, such as the Marchant, automated multiplication of up to 10-digit numbers. Modern electronic computer
A computer is a machine that can be Computer programming, programmed to automatically Execution (computing), carry out sequences of arithmetic or logical operations (''computation''). Modern digital electronic computers can perform generic set ...
s and calculators have greatly reduced the need for multiplication by hand.
Historical algorithms
Methods of multiplication were documented in the writings ofancient Egypt
Ancient Egypt () was a cradle of civilization concentrated along the lower reaches of the Nile River in Northeast Africa. It emerged from prehistoric Egypt around 3150BC (according to conventional Egyptian chronology), when Upper and Lower E ...
ian, and Chinese civilizations.
The Ishango bone, dated to about 18,000 to 20,000 BC, may hint at a knowledge of multiplication in the Upper Paleolithic
The Upper Paleolithic (or Upper Palaeolithic) is the third and last subdivision of the Paleolithic or Old Stone Age. Very broadly, it dates to between 50,000 and 12,000 years ago (the beginning of the Holocene), according to some theories ...
era in Central Africa
Central Africa (French language, French: ''Afrique centrale''; Spanish language, Spanish: ''África central''; Portuguese language, Portuguese: ''África Central'') is a subregion of the African continent comprising various countries accordin ...
, but this is speculative.
Egyptians
The Egyptian method of multiplication of integers and fractions, which is documented in the Rhind Mathematical Papyrus, was by successive additions and doubling. For instance, to find the product of 13 and 21 one had to double 21 three times, obtaining , , . The full product could then be found by adding the appropriate terms found in the doubling sequence: :13 × 21 = (1 + 4 + 8) × 21 = (1 × 21) + (4 × 21) + (8 × 21) = 21 + 84 + 168 = 273.Babylonians
The Babylonians used asexagesimal
Sexagesimal, also known as base 60, is a numeral system with 60 (number), sixty as its radix, base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified fo ...
positional number system, analogous to the modern-day decimal system. Thus, Babylonian multiplication was very similar to modern decimal multiplication. Because of the relative difficulty of remembering different products, Babylonian mathematicians employed multiplication tables. These tables consisted of a list of the first twenty multiples of a certain ''principal number'' ''n'': ''n'', 2''n'', ..., 20''n''; followed by the multiples of 10''n'': 30''n'' 40''n'', and 50''n''. Then to compute any sexagesimal product, say 53''n'', one only needed to add 50''n'' and 3''n'' computed from the table.
Chinese
Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 1st century CE. This book is one of the earliest surviving ...
'', multiplication calculations were written out in words, although the early Chinese mathematicians employed Rod calculus involving place value addition, subtraction, multiplication, and division. The Chinese were already using a decimal multiplication table by the end of the Warring States period.
Modern methods
The modern method of multiplication based on theHindu–Arabic numeral system
The Hindu–Arabic numeral system (also known as the Indo-Arabic numeral system, Hindu numeral system, and Arabic numeral system) is a positional notation, positional Decimal, base-ten numeral system for representing integers; its extension t ...
was first described by Brahmagupta
Brahmagupta ( – ) was an Indian Indian mathematics, mathematician and Indian astronomy, astronomer. He is the author of two early works on mathematics and astronomy: the ''Brāhmasphuṭasiddhānta'' (BSS, "correctly established Siddhanta, do ...
. Brahmagupta gave rules for addition, subtraction, multiplication, and division. Henry Burchard Fine, then a professor of mathematics at Princeton University
Princeton University is a private university, private Ivy League research university in Princeton, New Jersey, United States. Founded in 1746 in Elizabeth, New Jersey, Elizabeth as the College of New Jersey, Princeton is the List of Colonial ...
, wrote the following:
:''The Indians are the inventors not only of the positional decimal system itself, but of most of the processes involved in elementary reckoning with the system. Addition and subtraction they performed quite as they are performed nowadays; multiplication they effected in many ways, ours among them, but division they did cumbrously.''
These place value decimal arithmetic algorithms were introduced to Arab countries by Al Khwarizmi in the early 9th century and popularized in the Western world by Fibonacci
Leonardo Bonacci ( – ), commonly known as Fibonacci, was an Italians, Italian mathematician from the Republic of Pisa, considered to be "the most talented Western mathematician of the Middle Ages".
The name he is commonly called, ''Fibonacci ...
in the 13th century.
Grid method
Grid method multiplication, or the box method, is used in primary schools in England and Wales and in some areas of the United States to help teach an understanding of how multiple digit multiplication works. An example of multiplying 34 by 13 would be to lay the numbers out in a grid as follows: : and then add the entries.Computer algorithms
The classical method of multiplying two -digit numbers requires digit multiplications. Multiplication algorithms have been designed that reduce the computation time considerably when multiplying large numbers. Methods based on thediscrete Fourier transform
In mathematics, the discrete Fourier transform (DFT) converts a finite sequence of equally-spaced Sampling (signal processing), samples of a function (mathematics), function into a same-length sequence of equally-spaced samples of the discre ...
reduce the computational complexity to . In 2016, the factor was replaced by a function that increases much slower, though still not constant. In March 2019, David Harvey and Joris van der Hoeven submitted a paper presenting an integer multiplication algorithm with a complexity of The algorithm, also based on the fast Fourier transform, is conjectured to be asymptotically optimal. The algorithm is not practically useful, as it only becomes faster for multiplying extremely large numbers (having more than bits).
Products of measurements
One can only meaningfully add or subtract quantities of the same type, but quantities of different types can be multiplied or divided without problems. For example, four bags with three marbles each can be thought of as: : bags× marbles per bag= 12 marbles. When two measurements are multiplied together, the product is of a type depending on the types of measurements. The general theory is given by dimensional analysis. This analysis is routinely applied in physics, but it also has applications in finance and other applied fields. A common example in physics is the fact that multiplyingspeed
In kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a non-negative scalar quantity. Intro ...
by time
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequ ...
gives distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects, points, people, or ideas are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two co ...
. For example:
:50 kilometers per hour × 3 hours = 150 kilometers.
In this case, the hour units cancel out, leaving the product with only kilometer units.
Other examples of multiplication involving units include:
:2.5 meters × 4.5 meters = 11.25 square meters
:11 meters/seconds × 9 seconds = 99 meters
:4.5 residents per house × 20 houses = 90 residents
Product of a sequence
Capital pi notation
The product of a sequence of factors can be written with the product symbol , which derives from the capital letter Π (pi) in theGreek alphabet
The Greek alphabet has been used to write the Greek language since the late 9th or early 8th century BC. It was derived from the earlier Phoenician alphabet, and is the earliest known alphabetic script to systematically write vowels as wel ...
(much like the same way the summation symbol is derived from the Greek letter Σ (sigma)). The meaning of this notation is given by
:
which results in
:
In such a notation, the variable represents a varying integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
, called the multiplication index, that runs from the lower value indicated in the subscript to the upper value given by the superscript. The product is obtained by multiplying together all factors obtained by substituting the multiplication index for an integer between the lower and the upper values (the bounds included) in the expression that follows the product operator.
More generally, the notation is defined as
:
where ''m'' and ''n'' are integers or expressions that evaluate to integers. In the case where , the value of the product is the same as that of the single factor ''x''''m''; if , the product is an empty product
In mathematics, an empty product, or nullary product or vacuous product, is the result of multiplication, multiplying no factors. It is by convention equal to the multiplicative identity (assuming there is an identity for the multiplication operat ...
whose value is 1—regardless of the expression for the factors.
Properties of capital pi notation
By definition, : If all factors are identical, a product of factors is equivalent toexponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
:
:
Associativity
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replaceme ...
and commutativity
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a p ...
of multiplication imply
: and
:
if is a non-negative integer, or if all are positive real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s, and
:
if all are non-negative integers, or if is a positive real number.
Infinite products
One may also consider products of infinitely many factors; these are called '' infinite products''. Notationally, this consists in replacing ''n'' above by the infinity symbol ∞. The product of such an infinite sequence is defined as the limit of the product of the first ''n'' factors, as ''n'' grows without bound. That is, : One can similarly replace ''m'' with negative infinity, and define: : provided both limits exist.Exponentiation
When multiplication is repeated, the resulting operation is known as ''exponentiation
In mathematics, exponentiation, denoted , is an operation (mathematics), operation involving two numbers: the ''base'', , and the ''exponent'' or ''power'', . When is a positive integer, exponentiation corresponds to repeated multiplication ...
''. For instance, the product of three factors of two (2×2×2) is "two raised to the third power", and is denoted by 23, a two with a superscript
A subscript or superscript is a character (such as a number or letter) that is set slightly below or above the normal line of type, respectively. It is usually smaller than the rest of the text. Subscripts appear at or below the baseline, wh ...
three. In this example, the number two is the ''base'', and three is the ''exponent''. In general, the exponent (or superscript) indicates how many times the base appears in the expression, so that the expression
:
indicates that ''n'' copies of the base ''a'' are to be multiplied together. This notation can be used whenever multiplication is known to be power associative.
Properties
For real andcomplex
Complex commonly refers to:
* Complexity, the behaviour of a system whose components interact in multiple ways so possible interactions are difficult to describe
** Complex system, a system composed of many components which may interact with each ...
numbers, which includes, for example, natural number
In mathematics, the natural numbers are the numbers 0, 1, 2, 3, and so on, possibly excluding 0. Some start counting with 0, defining the natural numbers as the non-negative integers , while others start with 1, defining them as the positive in ...
s, integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s, and fractions, multiplication has certain properties:
; Commutative property
:The order in which two numbers are multiplied does not matter:
::
;Associative property
In mathematics, the associative property is a property of some binary operations that rearranging the parentheses in an expression will not change the result. In propositional logic, associativity is a Validity (logic), valid rule of replaceme ...
:Expressions solely involving multiplication or addition are invariant with respect to the order of operations
In mathematics and computer programming, the order of operations is a collection of rules that reflect conventions about which operations to perform first in order to evaluate a given mathematical expression.
These rules are formalized with a ...
:
::
;Distributive property
In mathematics, the distributive property of binary operations is a generalization of the distributive law, which asserts that the equality
x \cdot (y + z) = x \cdot y + x \cdot z
is always true in elementary algebra.
For example, in elementary ...
:Holds with respect to multiplication over addition. This identity is of prime importance in simplifying algebraic expressions:
::
;Identity element
In mathematics, an identity element or neutral element of a binary operation is an element that leaves unchanged every element when the operation is applied. For example, 0 is an identity element of the addition of real numbers. This concept is use ...
:The multiplicative identity is 1; anything multiplied by 1 is itself. This feature of 1 is known as the identity property:
::
; Property of 0
:Any number multiplied by 0 is 0. This is known as the zero property of multiplication:
::
;Negation
In logic, negation, also called the logical not or logical complement, is an operation (mathematics), operation that takes a Proposition (mathematics), proposition P to another proposition "not P", written \neg P, \mathord P, P^\prime or \over ...
:−1 times any number is equal to the additive inverse
In mathematics, the additive inverse of an element , denoted , is the element that when added to , yields the additive identity, 0 (zero). In the most familiar cases, this is the number 0, but it can also refer to a more generalized zero el ...
of that number:
::, where
:−1 times −1 is 1:
::
;Inverse element
In mathematics, the concept of an inverse element generalises the concepts of opposite () and reciprocal () of numbers.
Given an operation denoted here , and an identity element denoted , if , one says that is a left inverse of , and that ...
:Every number ''x'', except 0, has a multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a ra ...
, , such that .
; Order preservation
:Multiplication by a positive number preserves the order:
::For , if then .
:Multiplication by a negative number reverses the order:
::For , if then .
:The complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s do not have an ordering that is compatible with both addition and multiplication.
Other mathematical systems that include a multiplication operation may not have all these properties. For example, multiplication is not, in general, commutative for matrices and quaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s. Hurwitz's theorem shows that for the hypercomplex number
In mathematics, hypercomplex number is a traditional term for an element (mathematics), element of a finite-dimensional Algebra over a field#Unital algebra, unital algebra over a field, algebra over the field (mathematics), field of real numbers. ...
s of dimension
In physics and mathematics, the dimension of a mathematical space (or object) is informally defined as the minimum number of coordinates needed to specify any point within it. Thus, a line has a dimension of one (1D) because only one coo ...
8 or greater, including the octonions, sedenion
In abstract algebra, the sedenions form a 16-dimension of a vector space, dimensional commutative property, noncommutative and associative property, nonassociative algebra over a field, algebra over the real numbers, usually represented by the cap ...
s, and trigintaduonions, multiplication is generally not associative.
Axioms
In the book ''Arithmetices principia, nova methodo exposita
The 1889 treatise ''Arithmetices principia, nova methodo exposita'' (''The principles of arithmetic, presented by a new method'') by Giuseppe Peano is widely considered to be a seminal document in mathematical logic and set theory, introducin ...
'', Giuseppe Peano
Giuseppe Peano (; ; 27 August 1858 – 20 April 1932) was an Italian mathematician and glottologist. The author of over 200 books and papers, he was a founder of mathematical logic and set theory, to which he contributed much Mathematical notati ...
proposed axioms for arithmetic based on his axioms for natural numbers. Peano arithmetic has two axioms for multiplication:
:
:
Here ''S''(''y'') represents the successor of ''y''; i.e., the natural number that follows ''y''. The various properties like associativity can be proved from these and the other axioms of Peano arithmetic, including induction. For instance, ''S''(0), denoted by 1, is a multiplicative identity because
:
The axioms for integer
An integer is the number zero (0), a positive natural number (1, 2, 3, ...), or the negation of a positive natural number (−1, −2, −3, ...). The negations or additive inverses of the positive natural numbers are referred to as negative in ...
s typically define them as equivalence classes of ordered pairs of natural numbers. The model is based on treating (''x'',''y'') as equivalent to when ''x'' and ''y'' are treated as integers. Thus both (0,1) and (1,2) are equivalent to −1. The multiplication axiom for integers defined this way is
:
The rule that −1 × −1 = 1 can then be deduced from
:
Multiplication is extended in a similar way to rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
s and then to real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s.
Multiplication with set theory
The product of non-negative integers can be defined with set theory usingcardinal numbers
In mathematics, a cardinal number, or cardinal for short, is what is commonly called the number of elements of a set. In the case of a finite set, its cardinal number, or cardinality is therefore a natural number. For dealing with the case ...
or the Peano axioms
In mathematical logic, the Peano axioms (, ), also known as the Dedekind–Peano axioms or the Peano postulates, are axioms for the natural numbers presented by the 19th-century Italian mathematician Giuseppe Peano. These axioms have been used nea ...
. See below how to extend this to multiplying arbitrary integers, and then arbitrary rational numbers. The product of real numbers is defined in terms of products of rational numbers; see construction of the real numbers.
Multiplication in group theory
There are many sets that, under the operation of multiplication, satisfy the axioms that define group structure. These axioms are closure, associativity, and the inclusion of an identity element and inverses. A simple example is the set of non-zerorational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction (mathematics), fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for examp ...
. Here identity 1 is had, as opposed to groups under addition where the identity is typically 0. Note that with the rationals, zero must be excluded because, under multiplication, it does not have an inverse: there is no rational number that can be multiplied by zero to result in 1. In this example, an abelian group
In mathematics, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on the order in which they are written. That is, the group operation is commu ...
is had, but that is not always the case.
To see this, consider the set of invertible square matrices of a given dimension over a given field. Here, it is straightforward to verify closure, associativity, and inclusion of identity (the identity matrix
In linear algebra, the identity matrix of size n is the n\times n square matrix with ones on the main diagonal and zeros elsewhere. It has unique properties, for example when the identity matrix represents a geometric transformation, the obje ...
) and inverses. However, matrix multiplication is not commutative, which shows that this group is non-abelian.
Another fact worth noticing is that the integers under multiplication do not form a group—even if zero is excluded. This is easily seen by the nonexistence of an inverse for all elements other than 1 and −1.
Multiplication in group theory is typically notated either by a dot or by juxtaposition (the omission of an operation symbol between elements). So multiplying element a by element b could be notated as a b or ab. When referring to a group via the indication of the set and operation, the dot is used. For example, our first example could be indicated by .
Multiplication of different kinds of numbers
Numbers can ''count'' (3 apples), ''order'' (the 3rd apple), or ''measure'' (3.5 feet high); as the history of mathematics has progressed from counting on our fingers to modelling quantum mechanics, multiplication has been generalized to more complicated and abstract types of numbers, and to things that are not numbers (such as matrices) or do not look much like numbers (such asquaternion
In mathematics, the quaternion number system extends the complex numbers. Quaternions were first described by the Irish mathematician William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space. The algebra of quater ...
s).
; Integers
: is the sum of ''N'' copies of ''M'' when ''N'' and ''M'' are positive whole numbers. This gives the number of things in an array ''N'' wide and ''M'' high. Generalization to negative numbers can be done by
: and
:
: The same sign rules apply to rational and real numbers.
; Rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (for example,
The set of all ...
s
: Generalization to fractions is by multiplying the numerators and denominators, respectively: . This gives the area of a rectangle high and wide, and is the same as the number of things in an array when the rational numbers happen to be whole numbers.
; Real number
In mathematics, a real number is a number that can be used to measure a continuous one- dimensional quantity such as a duration or temperature. Here, ''continuous'' means that pairs of values can have arbitrarily small differences. Every re ...
s
: Real numbers and their products can be defined in terms of sequences of rational numbers.
; Complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
s
: Considering complex numbers and as ordered pairs of real numbers and , the product is . This is the same as for reals when the ''imaginary parts'' and are zero.
: Equivalently, denoting as ,
: Alternatively, in trigonometric form, if , then
; Further generalizations
: See Multiplication in group theory, above, and multiplicative group
In mathematics and group theory, the term multiplicative group refers to one of the following concepts:
*the group under multiplication of the invertible elements of a field, ring, or other structure for which one of its operations is referre ...
, which for example includes matrix multiplication. A very general, and abstract, concept of multiplication is as the "multiplicatively denoted" (second) binary operation in a ring. An example of a ring that is not any of the number systems above is a polynomial ring
In mathematics, especially in the field of algebra, a polynomial ring or polynomial algebra is a ring formed from the set of polynomials in one or more indeterminates (traditionally also called variables) with coefficients in another ring, ...
(polynomials can be added and multiplied, but polynomials are not numbers in any usual sense).
; Division
: Often division, , is the same as multiplication by an inverse, . Multiplication for some types of "numbers" may have corresponding division, without inverses; in an integral domain
In mathematics, an integral domain is a nonzero commutative ring in which the product of any two nonzero elements is nonzero. Integral domains are generalizations of the ring of integers and provide a natural setting for studying divisibilit ...
''x'' may have no inverse "" but may be defined. In a division ring
In algebra, a division ring, also called a skew field (or, occasionally, a sfield), is a nontrivial ring in which division by nonzero elements is defined. Specifically, it is a nontrivial ring in which every nonzero element has a multiplicativ ...
there are inverses, but may be ambiguous in non-commutative rings since need not be the same as .
See also
* Dimensional analysis * Multiplication algorithm ** Karatsuba algorithm, for large numbers ** Toom–Cook multiplication, for very large numbers ** Schönhage–Strassen algorithm, for huge numbers * Multiplication table * Binary multiplier, how computers multiply ** Booth's multiplication algorithm **Floating-point arithmetic
In computing, floating-point arithmetic (FP) is arithmetic on subsets of real numbers formed by a ''significand'' (a Sign (mathematics), signed sequence of a fixed number of digits in some Radix, base) multiplied by an integer power of that ba ...
** Multiply–accumulate operation
*** Fused multiply–add
** Wallace tree
* Multiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when Multiplication, multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a ra ...
, reciprocal
* Factorial
In mathematics, the factorial of a non-negative denoted is the Product (mathematics), product of all positive integers less than or equal The factorial also equals the product of n with the next smaller factorial:
\begin
n! &= n \times ...
* Genaille–Lucas rulers
* Lunar arithmetic
* Napier's bones
* Peasant multiplication
* Product (mathematics), for generalizations
* Slide rule
References
Further reading
*External links
Multiplication
an
Arithmetic Operations In Various Number Systems
at
cut-the-knot
Alexander Bogomolny (January 4, 1948 July 7, 2018) was a Soviet Union, Soviet-born Israeli Americans, Israeli-American mathematician. He was Professor Emeritus of Mathematics at the University of Iowa, and formerly research fellow at the Moscow ...
Modern Chinese Multiplication Techniques on an Abacus
{{Authority control Elementary arithmetic Mathematical notation Articles containing proofs