Multipole density formalism on:
[Wikipedia]
[Google]
[Amazon]

 The Multipole Density Formalism (also referred to as Hansen-Coppens Formalism) is an
The Multipole Density Formalism (also referred to as Hansen-Coppens Formalism) is an
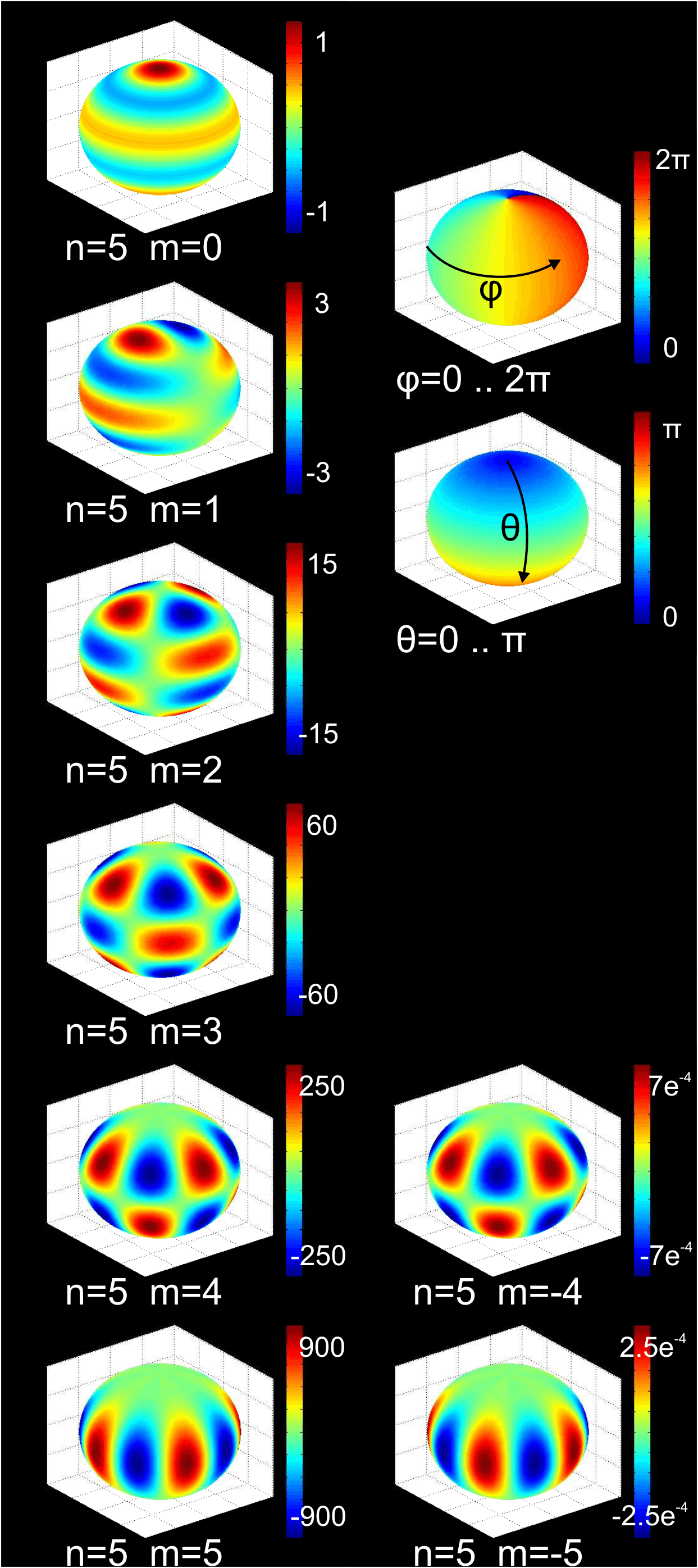
 The primary advantage of the Hansen-Coppens formalism is its ability to free the model from spherical restraints and describe the surroundings of a nucleus far more accurately. In this way it becomes possible to examine some molecular features which would normally be only roughly approximated or completely ignored.
The primary advantage of the Hansen-Coppens formalism is its ability to free the model from spherical restraints and describe the surroundings of a nucleus far more accurately. In this way it becomes possible to examine some molecular features which would normally be only roughly approximated or completely ignored.
SHADE
before introducing the formalism and, possibly, discarding bond distance constraints.
unphysical
parameter values. Applying additional constraints resulting from

 The Multipole Density Formalism (also referred to as Hansen-Coppens Formalism) is an
The Multipole Density Formalism (also referred to as Hansen-Coppens Formalism) is an X-ray crystallography
X-ray crystallography is the experimental science determining the atomic and molecular structure of a crystal, in which the crystalline structure causes a beam of incident X-rays to diffract into many specific directions. By measuring the angle ...
method of electron density
In quantum chemistry, electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial ...
modelling proposed by Niels K. Hansen
Niels is a male given name, equivalent to Nicholas, which is common in Denmark, Belgium, Norway (formerly) and the Netherlands. The Norwegian and Swedish variant is Nils. The name is a developed short form of Nicholas or Greek Nicolaos after Saint ...
and Philip Coppens in 1978. Unlike the commonly used Independent Atom Model, the Hansen-Coppens Formalism presents an aspherical approach, allowing one to model the electron
The electron (, or in nuclear reactions) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary partic ...
distribution around a nucleus
Nucleus ( : nuclei) is a Latin word for the seed inside a fruit. It most often refers to:
*Atomic nucleus, the very dense central region of an atom
* Cell nucleus, a central organelle of a eukaryotic cell, containing most of the cell's DNA
Nucl ...
separately in different directions and therefore describe numerous chemical features of a molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bio ...
inside the unit cell
In geometry, biology, mineralogy and solid state physics, a unit cell is a repeating unit formed by the vectors spanning the points of a lattice. Despite its suggestive name, the unit cell (unlike a unit vector, for example) does not necessari ...
of an examined crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macr ...
in detail.
Theory

Independent Atom Model
The Independent Atom Model (abbreviated to IAM), upon which the Multipole Model is based, is a method ofcharge density
In electromagnetism, charge density is the amount of electric charge per unit length, surface area, or volume. Volume charge density (symbolized by the Greek letter ρ) is the quantity of charge per unit volume, measured in the SI system in ...
modelling. It relies on an assumption that electron distribution around the atom
Every atom is composed of a nucleus and one or more electrons bound to the nucleus. The nucleus is made of one or more protons and a number of neutrons. Only the most common variety of hydrogen has no neutrons.
Every solid, liquid, gas ...
is isotropic, and that therefore charge density is dependent only on the distance from a nucleus. The choice of the radial function In mathematics, a radial function is a real-valued function defined on a Euclidean space R''n'' whose value at each point depends only on the distance between that point and the origin. The distance is usually the Euclidian distance. For example, ...
used to describe this electron density is arbitrary, granted that its value at the origin is finite. In practice either Gaussian- or Slater-type 1s-orbital functions are used.
Due to its simplistic approach, this method provides a straightforward model that requires no additional parameters (other than positional and Debye–Waller factor The Debye–Waller factor (DWF), named after Peter Debye and Ivar Waller, is used in condensed matter physics to describe the attenuation of x-ray scattering or coherent neutron scattering caused by thermal motion. It is also called the B factor, at ...
s) to be refined. This allows the IAM to perform satisfactorily while a relatively low amount of data from the diffraction experiment is available. However, the fixed shape of the singular basis function
In mathematics, a basis function is an element of a particular basis for a function space. Every function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be repre ...
prevents any detailed description of aspherical atomic features.
Kappa Formalism
In order to adjust somevalence shell
In chemistry and physics, a valence electron is an electron in the outer shell associated with an atom, and that can participate in the formation of a chemical bond if the outer shell is not closed. In a single covalent bond, a shared pair fo ...
parameters, the Kappa formalism was proposed. It introduces two additional refineable parameters: an outer shell population (denoted as ) and its expansion/contraction (). Therefore, the electron density is formulated as:
:
While , being responsible for the charge flow part, is linearly coupled with partial charge A partial charge is a non-integer charge value when measured in elementary charge units. Partial charge is more commonly called net atomic charge. It is represented by the Greek lowercase letter 𝛿, namely 𝛿− or 𝛿+.
Partial charges are cr ...
, the normalised parameter scales radial coordinate . Therefore, lowering the parameter results in expansion of the outer shell and, conversely, raising it results in contraction. Although the Kappa formalism is still, strictly speaking, a spherical method, it is an important step towards understanding modern approaches as it allows one to distinguish chemically different atoms of the same element.
Multipole description
In the multipole model description, the charge density around a nucleus is given by the following equation: : The spherical part remains almost indistinguishable from the Kappa formalism, the only difference being one parameter corresponding to the population of the inner shell. The real strength of the Hansen-Coppens formalism lies in the right, deformational part of the equation. Here fulfils a role similar to in the Kappa formalism (expansion/contraction of the aspherical part), whereas individual are fixed spherical functions, analogous to .Spherical harmonics
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
Since the spherical harmonics form a ...
(each with its populational parameter ) are, however, introduced to simulate the electrically anisotropic charge distribution.
In this approach, a fixed coordinate system for each atom needs to be applied. Although at first glance it seems practical to arbitrarily and indiscriminately make it contingent on the unit cell for all atoms present, it is far more beneficial to assign each atom its own local coordinates
Local coordinates are the ones used in a ''local coordinate system'' or a ''local coordinate space''. Simple examples:
* Houses. In order to work in a house construction, the measurements are referred to a control arbitrary point that will allow ...
, which allows for focusing on hybridisation-specific interactions
Interaction is action that occurs between two or more objects, with broad use in philosophy and the sciences. It may refer to:
Science
* Interaction hypothesis, a theory of second language acquisition
* Interaction (statistics)
* Interactions o ...
. While the singular sigma bond
In chemistry, sigma bonds (σ bonds) are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most simply defined for diatomic molecules using the language and tools o ...
of the hydrogen
Hydrogen is the chemical element with the symbol H and atomic number 1. Hydrogen is the lightest element. At standard conditions hydrogen is a gas of diatomic molecules having the formula . It is colorless, odorless, tasteless, non-toxic ...
can be described well using certain z-parallel pseudoorbitals, xy-plane oriented multipoles with a 3-fold rotational symmetry
Rotational symmetry, also known as radial symmetry in geometry, is the property a shape has when it looks the same after some rotation by a partial turn. An object's degree of rotational symmetry is the number of distinct orientations in which i ...
will prove more beneficial for flat aromatic
In chemistry, aromaticity is a chemical property of cyclic (ring-shaped), ''typically'' planar (flat) molecular structures with pi bonds in resonance (those containing delocalized electrons) that gives increased stability compared to sat ...
structures.
Applications
 The primary advantage of the Hansen-Coppens formalism is its ability to free the model from spherical restraints and describe the surroundings of a nucleus far more accurately. In this way it becomes possible to examine some molecular features which would normally be only roughly approximated or completely ignored.
The primary advantage of the Hansen-Coppens formalism is its ability to free the model from spherical restraints and describe the surroundings of a nucleus far more accurately. In this way it becomes possible to examine some molecular features which would normally be only roughly approximated or completely ignored.
Hydrogen positioning
X-ray crystallography allows the researcher to precisely determine the position of peak electron density and to reason about the placement of nuclei based on this information. This approach works without any problems for heavy (non-hydrogen) atoms, whose inner shell electrons contribute to the density function to a far greater degree then outer shell electrons. However, hydrogen atoms possess a feature unique among all the elements - they possess exactly one electron, which additionally is located on their valence shell and therefore is involved in creating strong covalent bonds with atoms of various other elements. While a bond is forming, the maximum of the electron density function moves significantly away from the nucleus and towards the other atom. This prevents any spherical approach from determining hydrogen position correctly by itself. Therefore, usually the hydrogen position is estimated basing on neutron crystallography data for similar molecules, or it is not modelled at all in the case of low-quality diffraction data. It is possible (albeit disputable) to freely refine hydrogen atoms' positions using the Hansen-Coppens formalism, after releasing the bond lengths from any restraints derived from neutron measurements. The bonding orbital simulated with adequate multipoles describes the density distribution neatly while preserving believable bond lengths. It may be worth approximating hydrogen atoms' anisotropic displacement parameters, e.g. usinSHADE
before introducing the formalism and, possibly, discarding bond distance constraints.
Bonding modelling
In order to analyse the length and strength of various interactions within the molecule, Richard Bader's " Atoms in molecules" theorem may be applied. Due to the complex description of the electron field provided by this aspherical model, it becomes possible to establish realistic bond paths between interacting atoms as well as to find and characterise their critical points. Deeper insight into this data yields useful information aboutbond strength
In chemistry, bond energy (''BE''), also called the mean bond enthalpy or average bond enthalpy is the measure of bond strength in a chemical bond. IUPAC defines bond energy as the average value of the gas-phase bond-dissociation energy (usually a ...
, type
Type may refer to:
Science and technology Computing
* Typing, producing text via a keyboard, typewriter, etc.
* Data type, collection of values used for computations.
* File type
* TYPE (DOS command), a command to display contents of a file.
* Ty ...
, polarity
Polarity may refer to:
Science
* Electrical polarity, direction of electrical current
* Polarity (mutual inductance), the relationship between components such as transformer windings
* Polarity (projective geometry), in mathematics, a duality of o ...
or ellipticity, and when compared with other molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bio ...
s brings greater understanding about the actual electron structure of the examined compound.
Charge flow
Due to the fact that for each multipole of every atom its population is being refined independently, individual charges will rarely beinteger
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
s. In real cases, electron density flows freely through the molecule and is not bound by any restrictions resulting from the outdated Bohr atom model
In atomic physics, the Bohr model or Rutherford–Bohr model, presented by Niels Bohr and Ernest Rutherford in 1913, is a system consisting of a small, dense nucleus surrounded by orbiting electrons—similar to the structure of the Solar Syste ...
and found in IAM. Therefore, through e.g. an accurate Bader analysis, net atomic charges may be estimated, which again is beneficial for deepening the understanding of systems under investigation.
Drawbacks and limitations
Although the Multipole Formalism is a simple and straightforward alternative means of structure refinement, it is definitely not flawless. While usually for each atom either three or nine parameters are to be refined, depending on whether an anisotropic displacement is being taken into account or not, a full multipole description of heavy atoms belonging to the fourth and subsequent periods (such aschlorine
Chlorine is a chemical element with the symbol Cl and atomic number 17. The second-lightest of the halogens, it appears between fluorine and bromine in the periodic table and its properties are mostly intermediate between them. Chlorine is ...
, iron
Iron () is a chemical element with symbol Fe (from la, ferrum) and atomic number 26. It is a metal that belongs to the first transition series and group 8 of the periodic table. It is, by mass, the most common element on Earth, right in ...
or bromine
Bromine is a chemical element with the symbol Br and atomic number 35. It is the third-lightest element in group 17 of the periodic table (halogens) and is a volatile red-brown liquid at room temperature that evaporates readily to form a simil ...
) requires refinement of up to 37 parameters. This proves problematic for any crystal
A crystal or crystalline solid is a solid material whose constituents (such as atoms, molecules, or ions) are arranged in a highly ordered microscopic structure, forming a crystal lattice that extends in all directions. In addition, macr ...
s possessing large asymmetric unit
In crystallography, crystal structure is a description of the ordered arrangement of atoms, ions or molecules in a crystalline material. Ordered structures occur from the intrinsic nature of the constituent particles to form symmetric patterns th ...
s (especially macromolecular
A macromolecule is a very large molecule important to biophysical processes, such as a protein or nucleic acid. It is composed of thousands of covalently bonded atoms. Many macromolecules are polymers of smaller molecules called monomers. The ...
compounds) and renders a refinement using the Hansen-Coppens Formalism unachievable for low-quality data with an unsatisfactory ratio of independent reflections to refined parameters.
Caution should be taken while refining some of the parameters simultaneously (i.e. or , multipole populations and thermal parameters), as they may correlate strongly, resulting in an unstable refinement ounphysical
parameter values. Applying additional constraints resulting from
local symmetry
In physics, a symmetry of a physical system is a physical or mathematical feature of the system (observed or intrinsic) that is preserved or remains unchanged under some transformation.
A family of particular transformations may be ''continuou ...
for each atom in a molecule (which decreases the number of refined multipoles) or importing populational parameters from existing databases may also be necessary to achieve a passable model. On the other hand, the aforementioned approaches significantly reduce the amount of information required from experiments, while preserving some level of detail concerning aspherical charge distribution. Therefore, even macromolecular
A macromolecule is a very large molecule important to biophysical processes, such as a protein or nucleic acid. It is composed of thousands of covalently bonded atoms. Many macromolecules are polymers of smaller molecules called monomers. The ...
structures with satisfactory X-ray diffraction data can be modelled aspherically in a similar fashion.
Despite their similarity, individual multipoles do not correspond to atomic projections of molecular orbitals of a wavefuntion as resulting from quantum calculations. Nevertheless, as brilliantly summarized by Stewart, "The structure of the model crystal density, as a superposition of pseudoatoms ..does have quantitative features which are close to many results based on quantum chemical calculations". If the overlap between the atomic wavefunctions is small enough, as it occurs for example in transition metal complexes, the atomic multipoles may be correlated with the atomic valence orbitals and multipolar coefficients may be correlated with populations of metal d-orbitals.
A stronger correlation between the X-ray measured diffracted intensities and quantum mechanical wavefunctions is possible using the wavefunction based methods of Quantum Crystallography, as for example the X-ray atomic orbital model, the so-called experimental wavefunction or the Hirshfeld Atom Refinement.
References
{{Reflist Theoretical chemistry X-ray crystallography Crystallography Diffraction