Mechanical Work on:
[Wikipedia]
[Google]
[Amazon]
In
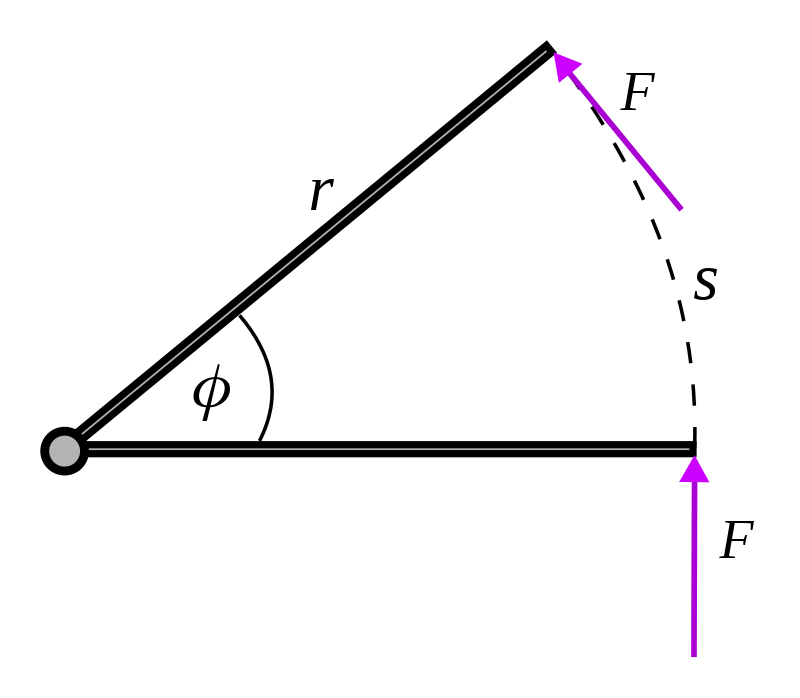 This result can be understood more simply by considering the torque as arising from a force of constant magnitude , being applied perpendicularly to a lever arm at a distance , as shown in the figure. This force will act through the distance along the circular arc , so the work done is
Introduce the torque , to obtain
as presented above.
Notice that only the component of torque in the direction of the angular velocity vector contributes to the work.
This result can be understood more simply by considering the torque as arising from a force of constant magnitude , being applied perpendicularly to a lever arm at a distance , as shown in the figure. This force will act through the distance along the circular arc , so the work done is
Introduce the torque , to obtain
as presented above.
Notice that only the component of torque in the direction of the angular velocity vector contributes to the work.
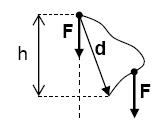 In the absence of other forces, gravity results in a constant downward acceleration of every freely moving object. Near Earth's surface the acceleration due to gravity is and the gravitational force on an object of mass ''m'' is . It is convenient to imagine this gravitational force concentrated at the center of mass of the object.
If an object with weight is displaced upwards or downwards a vertical distance , the work done on the object is:
where ''Fg'' is weight (pounds in imperial units, and newtons in SI units), and Δ''y'' is the change in height ''y''. Notice that the work done by gravity depends only on the vertical movement of the object. The presence of friction does not affect the work done on the object by its weight.
In the absence of other forces, gravity results in a constant downward acceleration of every freely moving object. Near Earth's surface the acceleration due to gravity is and the gravitational force on an object of mass ''m'' is . It is convenient to imagine this gravitational force concentrated at the center of mass of the object.
If an object with weight is displaced upwards or downwards a vertical distance , the work done on the object is:
where ''Fg'' is weight (pounds in imperial units, and newtons in SI units), and Δ''y'' is the change in height ''y''. Notice that the work done by gravity depends only on the vertical movement of the object. The presence of friction does not affect the work done on the object by its weight.
 Consider a spring that exerts a horizontal force that is proportional to its deflection in the ''x'' direction independent of how a body moves. The work of this spring on a body moving along the space with the curve , is calculated using its velocity, , to obtain
For convenience, consider contact with the spring occurs at , then the integral of the product of the distance and the x-velocity, , over time is . The work is the product of the distance times the spring force, which is also dependent on distance; hence the result.
Consider a spring that exerts a horizontal force that is proportional to its deflection in the ''x'' direction independent of how a body moves. The work of this spring on a body moving along the space with the curve , is calculated using its velocity, , to obtain
For convenience, consider contact with the spring occurs at , then the integral of the product of the distance and the x-velocity, , over time is . The work is the product of the distance times the spring force, which is also dependent on distance; hence the result.


Work–energy principle
{{Authority control Energy properties Scalar physical quantities Mechanical engineering Mechanics Force Length
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which rel ...
, work is the energy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of hea ...
transferred to or from an object via the application of force
In physics, a force is an influence that can change the motion of an object. A force can cause an object with mass to change its velocity (e.g. moving from a state of rest), i.e., to accelerate. Force can also be described intuitively as a ...
along a displacement. In its simplest form, for a constant force aligned with the direction of motion, the work equals the product of the force strength and the distance traveled. A force is said to do ''positive work'' if when applied it has a component in the direction of the displacement of the point of application. A force does ''negative work'' if it has a component opposite to the direction of the displacement at the point of application of the force.
For example, when a ball is held above the ground and then dropped, the work done by the gravitational force on the ball as it falls is positive, and is equal to the weight of the ball (a force) multiplied by the distance to the ground (a displacement). If the ball is thrown upwards, the work done by its weight is negative, and is equal to the weight multiplied by the displacement in the upwards direction.
When the force is constant and the angle between the force and the displacement is , then the work done is given by:
Work is a scalar quantity
Scalar may refer to:
*Scalar (mathematics), an element of a field, which is used to define a vector space, usually the field of real numbers
*Scalar (physics), a physical quantity that can be described by a single element of a number field such a ...
, so it has only magnitude and no direction. Work transfers energy from one place to another, or one form to another. The SI unit
The International System of Units, known by the international abbreviation SI in all languages and sometimes Pleonasm#Acronyms and initialisms, pleonastically as the SI system, is the modern form of the metric system and the world's most wid ...
of work is the joule
The joule ( , ; symbol: J) is the unit of energy in the International System of Units (SI). It is equal to the amount of work done when a force of 1 newton displaces a mass through a distance of 1 metre in the direction of the force applie ...
(J), the same unit as for energy.
History
The ancient Greek understanding of physics was limited to the statics of simple machines (the balance of forces), and did not include dynamics or the concept of work. During theRenaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass id ...
the dynamics of the ''Mechanical Powers'', as the simple machine
A simple machine is a mechanical device that changes the direction or magnitude of a force. In general, they can be defined as the simplest mechanisms that use mechanical advantage (also called leverage) to multiply force. Usually the term r ...
s were called, began to be studied from the standpoint of how far they could lift a load, in addition to the force they could apply, leading eventually to the new concept of mechanical work. The complete dynamic theory of simple machines was worked out by Italian scientist Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He w ...
in 1600 in ''Le Meccaniche'' (''On Mechanics''), in which he showed the underlying mathematical similarity of the machines as force amplifiers. He was the first to explain that simple machines do not create energy, only transform it.
Etymology
According to the 1957 physics textbook by Max Jammer, the term ''work'' was introduced in 1826 by the French mathematician Gaspard-Gustave Coriolis as "weight ''lifted'' through a height", which is based on the use of earlysteam engine
A steam engine is a heat engine that performs mechanical work using steam as its working fluid. The steam engine uses the force produced by steam pressure to push a piston back and forth inside a cylinder. This pushing force can be ...
s to lift buckets of water out of flooded ore mines. According to Rene Dugas, French engineer and historian, it is to Solomon of Caux "that we owe the term ''work'' in the sense that it is used in mechanics now".
Although ''work'' was not formally used until 1826, similar concepts existed before then. In 1759, John Smeaton described a quantity that he called "power" "to signify the exertion of strength, gravitation, impulse, or pressure, as to produce motion." Smeaton continues that this quantity can be calculated if "the weight raised is multiplied by the height to which it can be raised in a given time," making this definition remarkably similar to Coriolis'.
Units
The SI unit of work is thejoule
The joule ( , ; symbol: J) is the unit of energy in the International System of Units (SI). It is equal to the amount of work done when a force of 1 newton displaces a mass through a distance of 1 metre in the direction of the force applie ...
(J), named after the 19th-century English physicist James Prescott Joule, which is defined as the work required to exert a force of one newton through a displacement of one metre
The metre ( British spelling) or meter ( American spelling; see spelling differences) (from the French unit , from the Greek noun , "measure"), symbol m, is the primary unit of length in the International System of Units (SI), though its p ...
.
The dimensionally equivalent newton-metre (N⋅m) is sometimes used as the measuring unit for work, but this can be confused with the measurement unit of torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of t ...
. Usage of N⋅m is discouraged by the SI authority, since it can lead to confusion as to whether the quantity expressed in newton-metres is a torque measurement, or a measurement of work.
Non-SI units of work include the newton-metre, erg, the foot-pound, the foot-poundal, the kilowatt hour
A kilowatt-hour ( unit symbol: kW⋅h or kW h; commonly written as kWh) is a unit of energy: one kilowatt of power for one hour. In terms of SI derived units with special names, it equals 3.6 megajoules (MJ). Kilowatt-hours are a common bi ...
, the litre-atmosphere, and the horsepower-hour. Due to work having the same physical dimension
Size in general is the magnitude or dimensions of a thing. More specifically, ''geometrical size'' (or ''spatial size'') can refer to linear dimensions (length, width, height, diameter, perimeter), area, or volume. Size can also be measur ...
as heat
In thermodynamics, heat is defined as the form of energy crossing the boundary of a thermodynamic system by virtue of a temperature difference across the boundary. A thermodynamic system does not ''contain'' heat. Nevertheless, the term is ...
, occasionally measurement units typically reserved for heat or energy content, such as therm, BTU and calorie
The calorie is a unit of energy. For historical reasons, two main definitions of "calorie" are in wide use. The large calorie, food calorie, or kilogram calorie was originally defined as the amount of heat needed to raise the temperature of ...
, are used as a measuring unit.
Work and energy
The work done by a constant force of magnitude on a point that moves a displacement in a straight line in the direction of the force is the product For example, if a force of 10 newtons () acts along a point that travels 2 metres (), then . This is approximately the work done lifting a 1 kg object from ground level to over a person's head against the force of gravity. The work is doubled either by lifting twice the weight the same distance or by lifting the same weight twice the distance. Work is closely related toenergy
In physics, energy (from Ancient Greek: ἐνέργεια, ''enérgeia'', “activity”) is the quantitative property that is transferred to a body or to a physical system, recognizable in the performance of work and in the form of hea ...
. The work–energy principle states that an increase in the kinetic energy of a rigid body is caused by an equal amount of positive work done on the body by the resultant force acting on that body. Conversely, a decrease in kinetic energy is caused by an equal amount of negative work done by the resultant force. Thus, if the net work is positive, then the particle’s kinetic energy increases by the amount of the work. If the net work done is negative, then the particle’s kinetic energy decreases by the amount of work.
From Newton's second law
Newton's laws of motion are three basic Scientific law, laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at re ...
, it can be shown that work on a free (no fields), rigid (no internal degrees of freedom) body, is equal to the change in kinetic energy corresponding to the linear velocity and angular velocity of that body,
The work of forces generated by a potential function is known as potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
and the forces are said to be conservative
Conservatism is a cultural, social, and political philosophy that seeks to promote and to preserve traditional institutions, practices, and values. The central tenets of conservatism may vary in relation to the culture and civilization in ...
. Therefore, work on an object that is merely displaced in a conservative force field, without change in velocity or rotation, is equal to ''minus'' the change of potential energy of the object,
These formulas show that work is the energy associated with the action of a force, so work subsequently possesses the physical dimensions, and units, of energy.
The work/energy principles discussed here are identical to electric work/energy principles.
Constraint forces
Constraint forces determine the object's displacement in the system, limiting it within a range. For example, in the case of aslope
In mathematics, the slope or gradient of a line is a number that describes both the ''direction'' and the ''steepness'' of the line. Slope is often denoted by the letter ''m''; there is no clear answer to the question why the letter ''m'' is used ...
plus gravity, the object is ''stuck to'' the slope and, when attached to a taut string, it cannot move in an outwards direction to make the string any 'tauter'. It eliminates all displacements in that direction, that is, the velocity in the direction of the constraint is limited to 0, so that the constraint forces do not perform work on the system.
For a mechanical system, constraint forces eliminate movement in directions that characterize the constraint. Thus the virtual work done by the forces of constraint is zero, a result which is only true if friction forces are excluded.
Fixed, frictionless constraint forces do not perform work on the system, as the angle between the motion and the constraint forces is always 90°. Examples of workless constraints are: rigid interconnections between particles, sliding motion on a frictionless surface, and rolling contact without slipping.
For example, in a pulley system like the Atwood machine, the internal forces on the rope and at the supporting pulley do no work on the system. Therefore, work need only be computed for the gravitational forces acting on the bodies. Another example is the centripetal force exerted ''inwards'' by a string on a ball in uniform circular motion ''sideways'' constrains the ball to circular motion restricting its movement away from the centre of the circle. This force does zero work because it is perpendicular to the velocity of the ball.
The magnetic force on a charged particle is , where is the charge, is the velocity of the particle, and is the magnetic field
A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. A moving charge in a magnetic field experiences a force perpendicular to its own velocity and t ...
. The result of a cross product
In mathematics, the cross product or vector product (occasionally directed area product, to emphasize its geometric significance) is a binary operation on two vectors in a three-dimensional oriented Euclidean vector space (named here E), and i ...
is always perpendicular to both of the original vectors, so . The dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alg ...
of two perpendicular vectors is always zero, so the work , and the magnetic force does not do work. It can change the direction of motion but never change the speed.
Mathematical calculation
For moving objects, the quantity of work/time (power) is integrated along the trajectory of the point of application of the force. Thus, at any instant, the rate of the work done by a force (measured in joules/second, or watts) is the scalar product of the force (a vector), and the velocity vector of the point of application. This scalar product of force and velocity is known as instantaneous power. Just as velocities may be integrated over time to obtain a total distance, by thefundamental theorem of calculus
The fundamental theorem of calculus is a theorem that links the concept of differentiating a function (calculating its slopes, or rate of change at each time) with the concept of integrating a function (calculating the area under its graph, ...
, the total work along a path is similarly the time-integral of instantaneous power applied along the trajectory of the point of application.Resnick, Robert, Halliday, David (1966), ''Physics'', Section 1–3 (Vol I and II, Combined edition), Wiley International Edition, Library of Congress Catalog Card No. 66-11527
Work is the result of a force on a point that follows a curve , with a velocity , at each instant. The small amount of work that occurs over an instant of time is calculated as
where the is the power over the instant . The sum of these small amounts of work over the trajectory of the point yields the work,
where ''C'' is the trajectory from x(''t''1) to x(''t''2). This integral is computed along the trajectory of the particle, and is therefore said to be ''path dependent''.
If the force is always directed along this line, and the magnitude of the force is , then this integral simplifies to
where is displacement along the line. If is constant, in addition to being directed along the line, then the integral simplifies further to
where ''s'' is the displacement of the point along the line.
This calculation can be generalized for a constant force that is not directed along the line, followed by the particle. In this case the dot product
In mathematics, the dot product or scalar productThe term ''scalar product'' means literally "product with a scalar as a result". It is also used sometimes for other symmetric bilinear forms, for example in a pseudo-Euclidean space. is an alg ...
, where is the angle between the force vector and the direction of movement, that is
When a force component is perpendicular to the displacement of the object (such as when a body moves in a circular path under a central force), no work is done, since the cosine of 90° is zero. Thus, no work can be performed by gravity on a planet with a circular orbit (this is ideal, as all orbits are slightly elliptical). Also, no work is done on a body moving circularly at a constant speed while constrained by mechanical force, such as moving at constant speed in a frictionless ideal centrifuge.
Work done by a variable force
Calculating the work as "force times straight path segment" would only apply in the most simple of circumstances, as noted above. If force is changing, or if the body is moving along a curved path, possibly rotating and not necessarily rigid, then only the path of the application point of the force is relevant for the work done, and only the component of the force parallel to the application pointvelocity
Velocity is the directional speed of an object in motion as an indication of its rate of change in position as observed from a particular frame of reference and as measured by a particular standard of time (e.g. northbound). Velocity i ...
is doing work (positive work when in the same direction, and negative when in the opposite direction of the velocity). This component of force can be described by the scalar quantity called ''scalar tangential component'' (, where is the angle between the force and the velocity). And then the most general definition of work can be formulated as follows:
Torque and rotation
A force couple results from equal and opposite forces, acting on two different points of a rigid body. The sum (resultant) of these forces may cancel, but their effect on the body is the couple or torque T. The work of the torque is calculated as where the is the power over the instant . The sum of these small amounts of work over the trajectory of the rigid body yields the work, This integral is computed along the trajectory of the rigid body with an angular velocity that varies with time, and is therefore said to be ''path dependent''. If the angular velocity vector maintains a constant direction, then it takes the form, where is the angle of rotation about the constant unit vector . In this case, the work of the torque becomes, where is the trajectory from to . This integral depends on the rotational trajectory , and is therefore path-dependent. If the torque is aligned with the angular velocity vector so that, and both the torque and angular velocity are constant, then the work takes the form, This result can be understood more simply by considering the torque as arising from a force of constant magnitude , being applied perpendicularly to a lever arm at a distance , as shown in the figure. This force will act through the distance along the circular arc , so the work done is
Introduce the torque , to obtain
as presented above.
Notice that only the component of torque in the direction of the angular velocity vector contributes to the work.
This result can be understood more simply by considering the torque as arising from a force of constant magnitude , being applied perpendicularly to a lever arm at a distance , as shown in the figure. This force will act through the distance along the circular arc , so the work done is
Introduce the torque , to obtain
as presented above.
Notice that only the component of torque in the direction of the angular velocity vector contributes to the work.
Work and potential energy
The scalar product of a force and the velocity of its point of application defines the power input to a system at an instant of time. Integration of this power over the trajectory of the point of application, , defines the work input to the system by the force.Path dependence
Therefore, the work done by a force on an object that travels along a curve is given by the line integral: where defines the trajectory and is the velocity along this trajectory. In general this integral requires that the path along which the velocity is defined, so the evaluation of work is said to be path dependent. The time derivative of the integral for work yields the instantaneous power,Path independence
If the work for an applied force is independent of the path, then the work done by the force, by the gradient theorem, defines a potential function which is evaluated at the start and end of the trajectory of the point of application. This means that there is a potential function , that can be evaluated at the two points and to obtain the work over any trajectory between these two points. It is tradition to define this function with a negative sign so that positive work is a reduction in the potential, that is The function is called thepotential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
associated with the applied force. The force derived from such a potential function is said to be conservative
Conservatism is a cultural, social, and political philosophy that seeks to promote and to preserve traditional institutions, practices, and values. The central tenets of conservatism may vary in relation to the culture and civilization in ...
. Examples of forces that have potential energies are gravity and spring forces.
In this case, the gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
of work yields
and the force F is said to be "derivable from a potential."
Because the potential defines a force at every point in space, the set of forces is called a force field. The power applied to a body by a force field is obtained from the gradient of the work, or potential, in the direction of the velocity of the body, that is
Work by gravity
Work by gravity in space
The force of gravity exerted by a mass on another mass is given by where is the position vector from to and is the unit vector in the direction of . Let the mass move at the velocity ; then the work of gravity on this mass as it moves from position to is given by Notice that the position and velocity of the mass are given by where and are the radial and tangential unit vectors directed relative to the vector from to , and we use the fact that Use this to simplify the formula for work of gravity to, This calculation uses the fact that The function is the gravitational potential function, also known asgravitational potential energy
Gravitational energy or gravitational potential energy is the potential energy a massive object has in relation to another massive object due to gravity. It is the potential energy associated with the gravitational field, which is released (conv ...
. The negative sign follows the convention that work is gained from a loss of potential energy.
Work by a spring
Work by a gas
The work done by a body of gas on its surroundings is: where is pressure, is volume, and and are initial and final volumes.Work–energy principle
The principle of work andkinetic energy
In physics, the kinetic energy of an object is the energy that it possesses due to its motion.
It is defined as the work needed to accelerate a body of a given mass from rest to its stated velocity. Having gained this energy during its a ...
(also known as the work–energy principle) states that ''the work done by all forces acting on a particle (the work of the resultant force) equals the change in the kinetic energy of the particle.'' That is, the work ''W'' done by the resultant force on a particle
In the physical sciences, a particle (or corpuscule in older texts) is a small localized object which can be described by several physical or chemical properties, such as volume, density, or mass.
They vary greatly in size or quantity, fro ...
equals the change in the particle's kinetic energy ,
where and are the speed
In everyday use and in kinematics, the speed (commonly referred to as ''v'') of an object is the magnitude of the change of its position over time or the magnitude of the change of its position per unit of time; it is thus a scalar quantity ...
s of the particle before and after the work is done, and is its mass
Mass is an intrinsic property of a body. It was traditionally believed to be related to the quantity of matter in a physical body, until the discovery of the atom and particle physics. It was found that different atoms and different element ...
.
The derivation of the ''work–energy principle'' begins with Newton’s second law of motion and the resultant force on a particle. Computation of the scalar product of the forces with the velocity of the particle evaluates the instantaneous power added to the system.
Constraints define the direction of movement of the particle by ensuring there is no component of velocity in the direction of the constraint force. This also means the constraint forces do not add to the instantaneous power. The time integral of this scalar equation yields work from the instantaneous power, and kinetic energy from the scalar product of velocity and acceleration. The fact that the work–energy principle eliminates the constraint forces underlies Lagrangian mechanics
In physics, Lagrangian mechanics is a formulation of classical mechanics founded on the stationary-action principle (also known as the principle of least action). It was introduced by the Italian-French mathematician and astronomer Joseph-Lou ...
.
This section focuses on the work–energy principle as it applies to particle dynamics. In more general systems work can change the potential energy
In physics, potential energy is the energy held by an object because of its position relative to other objects, stresses within itself, its electric charge, or other factors.
Common types of potential energy include the gravitational potentia ...
of a mechanical device, the thermal energy in a thermal system, or the electrical energy
Electrical energy is energy related to forces on electrically charged particles and the movement of electrically charged particles (often electrons in wires, but not always). This energy is supplied by the combination of electric current and electr ...
in an electrical device. Work transfers energy from one place to another or one form to another.
Derivation for a particle moving along a straight line
In the case the resultant force is constant in both magnitude and direction, and parallel to the velocity of the particle, the particle is moving with constant acceleration ''a'' along a straight line. The relation between the net force and the acceleration is given by the equation (Newton's second law
Newton's laws of motion are three basic Scientific law, laws of classical mechanics that describe the relationship between the motion of an object and the forces acting on it. These laws can be paraphrased as follows:
# A body remains at re ...
), and the particle displacement can be expressed by the equation
which follows from (see Equations of motion).
The work of the net force is calculated as the product of its magnitude and the particle displacement. Substituting the above equations, one obtains:
Other derivation:
In the general case of rectilinear motion, when the net force is not constant in magnitude, but is constant in direction, and parallel to the velocity of the particle, the work must be integrated along the path of the particle:
General derivation of the work–energy principle for a particle
For any net force acting on a particle moving along any curvilinear path, it can be demonstrated that its work equals the change in the kinetic energy of the particle by a simple derivation analogous to the equation above. It is known as the work–energy principle: The identity requires some algebra. From the identity and definition it follows The remaining part of the above derivation is just simple calculus, same as in the preceding rectilinear case.Derivation for a particle in constrained movement
In particle dynamics, a formula equating work applied to a system to its change in kinetic energy is obtained as a first integral of Newton's second law of motion. It is useful to notice that the resultant force used in Newton's laws can be separated into forces that are applied to the particle and forces imposed by constraints on the movement of the particle. Remarkably, the work of a constraint force is zero, therefore only the work of the applied forces need be considered in the work–energy principle. To see this, consider a particle P that follows the trajectory with a force acting on it. Isolate the particle from its environment to expose constraint forces , then Newton's Law takes the form where is the mass of the particle.Vector formulation
Note that n dots above a vector indicates its nth time derivative. The scalar product of each side of Newton's law with the velocity vector yields because the constraint forces are perpendicular to the particle velocity. Integrate this equation along its trajectory from the point to the point to obtain The left side of this equation is the work of the applied force as it acts on the particle along the trajectory from time to time . This can also be written as This integral is computed along the trajectory of the particle and is therefore path dependent. The right side of the first integral of Newton's equations can be simplified using the following identity (see product rule for derivation). Now it is integrated explicitly to obtain the change in kinetic energy, where the kinetic energy of the particle is defined by the scalar quantity,Tangential and normal components
It is useful to resolve the velocity and acceleration vectors into tangential and normal components along the trajectory , such that where Then, the scalar product of velocity with acceleration in Newton's second law takes the form where the kinetic energy of the particle is defined by the scalar quantity, The result is the work–energy principle for particle dynamics, This derivation can be generalized to arbitrary rigid body systems.Moving in a straight line (skid to a stop)
Consider the case of a vehicle moving along a straight horizontal trajectory under the action of a driving force and gravity that sum to . The constraint forces between the vehicle and the road define , and we have For convenience let the trajectory be along the X-axis, so and the velocity is , then , and , where ''F''x is the component of F along the X-axis, so Integration of both sides yields If is constant along the trajectory, then the integral of velocity is distance, so As an example consider a car skidding to a stop, where ''k'' is the coefficient of friction and ''W'' is the weight of the car. Then the force along the trajectory is . The velocity ''v'' of the car can be determined from the length of the skid using the work–energy principle, Notice that this formula uses the fact that the mass of the vehicle is .

Coasting down an inclined surface (gravity racing)
Consider the case of a vehicle that starts at rest and coasts down an inclined surface (such as mountain road), the work–energy principle helps compute the minimum distance that the vehicle travels to reach a velocity , of say 60 mph (88 fps). Rolling resistance and air drag will slow the vehicle down so the actual distance will be greater than if these forces are neglected. Let the trajectory of the vehicle following the road be which is a curve in three-dimensional space. The force acting on the vehicle that pushes it down the road is the constant force of gravity , while the force of the road on the vehicle is the constraint force . Newton's second law yields, The scalar product of this equation with the velocity, , yields where is the magnitude of . The constraint forces between the vehicle and the road cancel from this equation because , which means they do no work. Integrate both sides to obtain The weight force ''W'' is constant along the trajectory and the integral of the vertical velocity is the vertical distance, therefore, Recall that V(''t''1)=0. Notice that this result does not depend on the shape of the road followed by the vehicle. In order to determine the distance along the road assume the downgrade is 6%, which is a steep road. This means the altitude decreases 6 feet for every 100 feet traveled—for angles this small the sin and tan functions are approximately equal. Therefore, the distance in feet down a 6% grade to reach the velocity is at least This formula uses the fact that the weight of the vehicle is .Work of forces acting on a rigid body
The work of forces acting at various points on a single rigid body can be calculated from the work of a resultant force and torque. To see this, let the forces F1, F2, ..., Fn act on the points X1, X2, ..., X''n'' in a rigid body. The trajectories of X''i'', ''i'' = 1, ..., ''n'' are defined by the movement of the rigid body. This movement is given by the set of rotations 'A''(''t'')and the trajectory d(''t'') of a reference point in the body. Let the coordinates x''i'' ''i'' = 1, ..., ''n'' define these points in the moving rigid body's reference frame ''M'', so that the trajectories traced in the fixed frame ''F'' are given by The velocity of the points along their trajectories are where is the angular velocity vector obtained from the skew symmetric matrix known as the angular velocity matrix. The small amount of work by the forces over the small displacements can be determined by approximating the displacement by so or This formula can be rewritten to obtain where F and T are the resultant force and torque applied at the reference point d of the moving frame ''M'' in the rigid body.References
Bibliography
* *External links
Work–energy principle
{{Authority control Energy properties Scalar physical quantities Mechanical engineering Mechanics Force Length