Klumpenhouwer Network on:
[Wikipedia]
[Google]
[Amazon]
 A Klumpenhouwer Network, named after its inventor, Canadian
A Klumpenhouwer Network, named after its inventor, Canadian  "Klumpenhouwer's idea, both simple and profound in its implications, is to allow inversional, as well as transpositional, relations into networks like those of Figure 1," showing an arrow down from B to F labeled T7, down from F to A labeled T3, and back up from A to B, labeled T10 which allows it to be represented by Figure 2a, for example, labeled I5, I3, and T2. In Figure 4 this is (b) I7, I5, T2 and (c) I5, I3, T2.
"Klumpenhouwer's idea, both simple and profound in its implications, is to allow inversional, as well as transpositional, relations into networks like those of Figure 1," showing an arrow down from B to F labeled T7, down from F to A labeled T3, and back up from A to B, labeled T10 which allows it to be represented by Figure 2a, for example, labeled I5, I3, and T2. In Figure 4 this is (b) I7, I5, T2 and (c) I5, I3, T2.


 ]
Lewin asserts the " recursion, recursive potential of K-network analysis"Lewin, David (1994). "A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg's Opus 11, No. 2", p. 90, ''
]
Lewin asserts the " recursion, recursive potential of K-network analysis"Lewin, David (1994). "A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg's Opus 11, No. 2", p. 90, ''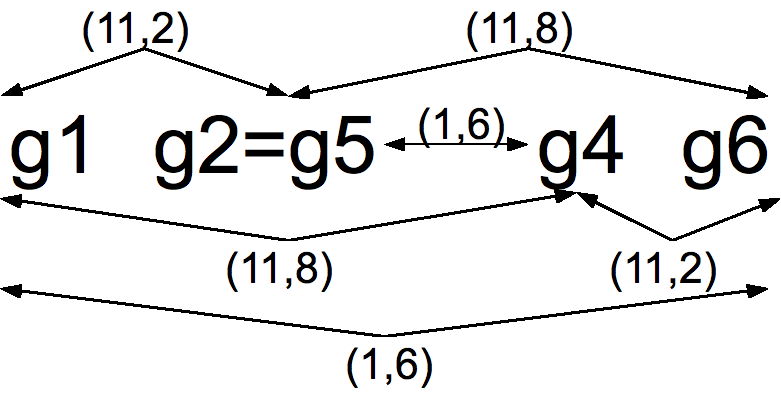 Other terms include ''Lewin Transformational Network'' and ''strongly
Other terms include ''Lewin Transformational Network'' and ''strongly
music theorist
Music theory is the study of the practices and possibilities of music. ''The Oxford Companion to Music'' describes three interrelated uses of the term "music theory". The first is the "rudiments", that are needed to understand music notation (ke ...
and former doctoral student of David Lewin
David Benjamin Lewin (July 2, 1933 – May 5, 2003) was an American music theorist, music critic and composer. Called "the most original and far-ranging theorist of his generation", he did his most influential theoretical work on the development of ...
's at Harvard
Harvard University is a private Ivy League research university in Cambridge, Massachusetts. Founded in 1636 as Harvard College and named for its first benefactor, the Puritan clergyman John Harvard, it is the oldest institution of higher le ...
, Henry Klumpenhouwer Henry Klumpenhouwer is a Canadian musicologist and former professor at the University of Alberta. He currently teaches at the Eastman School of Music. A former PhD student of David Lewin and the inventor of Klumpenhouwer networks, which are named a ...
, is "any network
Network, networking and networked may refer to:
Science and technology
* Network theory, the study of graphs as a representation of relations between discrete objects
* Network science, an academic field that studies complex networks
Mathematics
...
that uses T and/or I operations ( transposition or inversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
) to interpret interrelations among pcs" (pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
sets).Lewin, David (1990). "Klumpenhouwer Networks and Some Isographies That Involve Them", p. 84, ''Music Theory Spectrum
''Music Theory Spectrum'' () is a peer-reviewed, academic journal specializing in music theory and analysis. It is the official journal of the Society for Music Theory, and is published by Oxford University Press. The journal was first published ...
'', vol. 12, no. 1 (Spring), pp. 83–120. According to George Perle
George Perle (6 May 1915 – 23 January 2009) was an American composer and music theorist. As a composer, his music was largely atonal, using methods similar to the twelve-tone technique of the Second Viennese School. This serialist style, an ...
, "a Klumpenhouwer network is a chord analyzed in terms of its dyadic sums
In mathematics, summation is the addition of a sequence of any kind of numbers, called ''addends'' or ''summands''; the result is their ''sum'' or ''total''. Beside numbers, other types of values can be summed as well: function (mathematics), fu ...
and differences," and "this kind of analysis of triadic combinations was implicit in," his "concept of the cyclic set from the beginning", Perle, George (1993). "Letter from George Perle", ''Music Theory Spectrum
''Music Theory Spectrum'' () is a peer-reviewed, academic journal specializing in music theory and analysis. It is the official journal of the Society for Music Theory, and is published by Oxford University Press. The journal was first published ...
'', vol. 15, no. 2 (Autumn), pp. 300–303. cyclic sets being those " sets whose alternate elements unfold complementary
A complement is something that completes something else.
Complement may refer specifically to:
The arts
* Complement (music), an interval that, when added to another, spans an octave
** Aggregate complementation, the separation of pitch-class ...
cycles of a single interval."
 "Klumpenhouwer's idea, both simple and profound in its implications, is to allow inversional, as well as transpositional, relations into networks like those of Figure 1," showing an arrow down from B to F labeled T7, down from F to A labeled T3, and back up from A to B, labeled T10 which allows it to be represented by Figure 2a, for example, labeled I5, I3, and T2. In Figure 4 this is (b) I7, I5, T2 and (c) I5, I3, T2.
"Klumpenhouwer's idea, both simple and profound in its implications, is to allow inversional, as well as transpositional, relations into networks like those of Figure 1," showing an arrow down from B to F labeled T7, down from F to A labeled T3, and back up from A to B, labeled T10 which allows it to be represented by Figure 2a, for example, labeled I5, I3, and T2. In Figure 4 this is (b) I7, I5, T2 and (c) I5, I3, T2.


 ]
Lewin asserts the " recursion, recursive potential of K-network analysis"Lewin, David (1994). "A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg's Opus 11, No. 2", p. 90, ''
]
Lewin asserts the " recursion, recursive potential of K-network analysis"Lewin, David (1994). "A Tutorial on Klumpenhouwer Networks, Using the Chorale in Schoenberg's Opus 11, No. 2", p. 90, ''Journal of Music Theory
The ''Journal of Music Theory'' is a peer-reviewed academic journal specializing in music theory and analysis. It was established by David Kraehenbuehl (Yale University) in 1957.
According to its website, " e ''Journal of Music Theory'' fosters c ...
'', vol. 38, no. 1 (Spring), pp. 79–101.... "'in great generality: When a system modulates by an operation A, the transformation f = A f A -inverse plays the structural role in the modulated system that f played in the original system."
Given any network of pitch class
In music, a pitch class (p.c. or pc) is a set of all pitches that are a whole number of octaves apart; for example, the pitch class C consists of the Cs in all octaves. "The pitch class C stands for all possible Cs, in whatever octave positio ...
es, and given any pc operation A, a second network may be derived from the first, and the relationship thereby derived 'network isomorphism' "arises between networks using analogous configurations of nodes
In general, a node is a localized swelling (a "knot") or a point of intersection (a Vertex (graph theory), vertex).
Node may refer to:
In mathematics
*Vertex (graph theory), a vertex in a mathematical graph
*Vertex (geometry), a point where two ...
and arrows to interpret pcsets that are of the same set classLewin (1990), p. 87. – 'isomorphism of graphs'. Two graphs are ''isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
'' when they share the same structure of nodes-and-arrows, and when also the operations labeling corresponding arrows correspond under a particular sort of mapping f among T/I."Lewin (1990), p. 88.
"To generate isomorphic graphs, the mapping f must be what is called an ''automorphism'' of the T/I system. Networks that have isomorphic graphs are called ''isographic''."
To be isographic, two networks must have these features:
#They must have the same configuration of nodes and arrows.
#There must be some isomorphism
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
F that maps the transformation
Transformation may refer to:
Science and mathematics
In biology and medicine
* Metamorphosis, the biological process of changing physical form after birth or hatching
* Malignant transformation, the process of cells becoming cancerous
* Trans ...
-system used to label the arrows of one network, into the transformation-system used to label the arrows of the other.
#If the transformation X labels an arrow of the one network, then the transformation F(X) labels the corresponding arrow of the other."
"Two networks are ''positively isographic'' when they share the same configuration of nodes and arrows, when the T-numbers of corresponding arrows are equal, and when the I-numbers of corresponding arrows differ by some fixed number j mod 12." "We call networks that contain identical graphs 'strongly isographic'". "Let the family of transpositions and inversions on pitch classes be called 'the T/I group.'"Lewin (1990, 86).
"Any network can be ''retrograded'' by reversing all arrows and adjusting the transformations accordingly."
Klumpenhouwer's rue
''Ruta graveolens'', commonly known as rue, common rue or herb-of-grace, is a species of '' Ruta'' grown as an ornamental plant and herb. It is native to the Balkan Peninsula. It is grown throughout the world in gardens, especially for its bl ...
conjecture: "nodes (a) and (b), sharing the same configuration of arrows, will always be isographic if each T-number of Network (b) is the same as the corresponding T-number of Network (a), while each I-number of Network (b) is exactly j more than the corresponding I-number of Network (a), where j is some constant number modulo 12."
Five Rules for Isography of Klumpenhouwer Networks:
#Klumpenhouwer Networks (a) and (b), sharing the same configuration of nodes and arrows, will be isographic under the circumstance that each T-number of Network (b) is the same as the corresponding T-number of Network (a), and each I-number of Network (b) is exactly j more than the corresponding I-number of Network (a). The pertinent automorphism of the T/I group is F(1,j): F(1,j)(Tn)=Tn; F(1,j)(In) = In+J.
#Klumpenhouwer Networks (a) and (b), will be isographic under the circumstance that each T-number of Network (b) is the complement of the corresponding T-number in Network (a), and each I-number of Network (b) is exactly j more than the complement of the corresponding I-number in Network (a)...F(11,j): F(11,j)(Tn)=T−n; F(11,j)(In)=I−n+j."
#Klumpenhouwer Networks (a) and (b), will be isographic under the circumstance each T-number of Network (b) is 5 times the corresponding T-number in Network (a), and each I-number of Network (b) is exactly j more than 5 times the corresponding I-number in Network (a)...F(5,j): F(5,j)(Tn)=T5n; F(5,j)(In)=I5n+j.Lewin (1990), p. 88.
#Klumpenhouwer Networks (a) and (b), will be isographic under the circumstance each T-number of Network (b) is 7 times the corresponding T-number in Network (a), and each I-number of Network (b) is exactly j more than 7 times the corresponding I-number in Network (a)...F(7,j): F(7,j)(Tn)=T7n; F(7,j)(In)=I7n+j.
#"Klumpenhouwer Networks (a) and (b), even if sharing the same configuration of nodes and arrows, will not be isographic under any other circumstances."
"Any one of Klupmenhouwer's triadic networks may thus be understood as a segment of cyclic set, and the interpretations of these and of the 'networks of networks'...efficiently and economically represented in this way."
If the graphs of chords are isomorphic by way of the appropriate F(u,j) operations, then they may be graphed as their own network.Lewin (1990, 92).
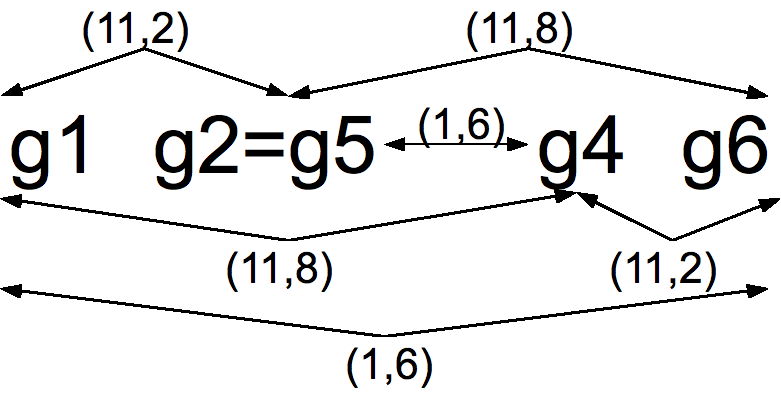 Other terms include ''Lewin Transformational Network'' and ''strongly
Other terms include ''Lewin Transformational Network'' and ''strongly isomorphic
In mathematics, an isomorphism is a structure-preserving mapping between two structures of the same type that can be reversed by an inverse mapping. Two mathematical structures are isomorphic if an isomorphism exists between them. The word is ...
''.
See also
*Interval class
In musical set theory, an interval class (often abbreviated: ic), also known as unordered pitch-class interval, interval distance, undirected interval, or "(even completely incorrectly) as 'interval mod 6'" (; ), is the shortest distance in pitch ...
* Isography
*Similarity relation __NOTOC__
In music, a similarity relation or pitch-class similarity is a comparison between sets of the same cardinality (two sets containing the same number of pitch classes), based upon shared pitch class and/or interval class content.
Allen F ...
*Tone row
In music, a tone row or note row (german: Reihe or '), also series or set, is a non-repetitive ordering of a set of pitch-classes, typically of the twelve notes in musical set theory of the chromatic scale, though both larger and smaller sets ar ...
*Transformation (music)
In music, a transformation consists of any operation or process that may apply to a musical variable (usually a set or tone row in twelve tone music, or a melody or chord progression in tonal music), or rhythm in composition, performance, or anal ...
*Lewin's Transformational theory
Transformational theory is a branch of music theory developed by David Lewin in the 1980s, and formally introduced in his 1987 work, ''Generalized Musical Intervals and Transformations''. The theory—which models musical transformations as ele ...
.
*Prolongation
In music theory, prolongation is the process in tonal music through which a pitch, interval, or consonant triad is considered to govern spans of music when not physically sounding. It is a central principle in the music-analytic methodology of ...
Further reading
*in ''Generalized Musical Intervals and Transformations'' (New Haven and London: Yale University Press, 1987), 159–160, David Lewin discusses "a related network involving pitches and pitch intervals, rather than pitch classes and pc interval". *Donald Martino
Donald James Martino (May 16, 1931 – December 8, 2005) was a Pulitzer Prize winning American composer.
Biography
Born in Plainfield, New Jersey, Martino attended Plainfield High School. He began as a clarinetist, playing jazz for fun and p ...
(1961), "The Source Set and Its Aggregate
Aggregate or aggregates may refer to:
Computing and mathematics
* collection of objects that are bound together by a root entity, otherwise known as an aggregate root. The aggregate root guarantees the consistency of changes being made within the ...
Formations", ''Journal of Music Theory
The ''Journal of Music Theory'' is a peer-reviewed academic journal specializing in music theory and analysis. It was established by David Kraehenbuehl (Yale University) in 1957.
According to its website, " e ''Journal of Music Theory'' fosters c ...
'' 5, no. 2 (Fall): 224–273.
*Allen Forte Allen, Allen's or Allens may refer to:
Buildings
* Allen Arena, an indoor arena at Lipscomb University in Nashville, Tennessee
* Allen Center, a skyscraper complex in downtown Houston, Texas
* Allen Fieldhouse, an indoor sports arena on the Univer ...
, ''The Structure of Atonal Music'' (New Haven: Yale University Press, 1973).
*John Rahn
John Rahn, born on February 26, 1944, in New York City, is a music theorist, composer, bassoonist, and Professor of Music at the University of Washington School of Music, Seattle. A former student of Milton Babbitt and Benjamin Boretz, he was edito ...
, ''Basic Atonal Theory'' (New York and London: Longman's, 1980).Klumpenhouwer, Henry (1991). "Aspects of Row Structure and Harmony in Martino's Impromptu Number 6", p. 318n1, ''Perspectives of New Music
''Perspectives of New Music'' (PNM) is a peer-reviewed academic journal specializing in music theory and analysis. It was established in 1962 by Arthur Berger and Benjamin Boretz (who were its initial editors-in-chief).
''Perspectives'' was first ...
'', vol. 29, no. 2 (Summer), pp. 318–354.
*Roeder, John (1989). "Harmonic Implications of Schönberg's Observations of Atonal Voice Leading", ''Journal of Music Theory
The ''Journal of Music Theory'' is a peer-reviewed academic journal specializing in music theory and analysis. It was established by David Kraehenbuehl (Yale University) in 1957.
According to its website, " e ''Journal of Music Theory'' fosters c ...
'' 33, no. 1 (Spring): 27–62.cited in Klumpenhouwer (1991), p. 354: "Roeder is mostly, though not exclusively, interested in common-tone relations between pairs of chords whose constitutive pitches are related in ways he formalizes from remarks in Schönberg's ''Harmonielehre
''Harmonielehre'' is a forty-minute orchestral composition by the American composer John Adams, composed in 1985. In his memoir, Adams stated that the piece "was a statement of belief in the power of tonality at a time when I was uncertain about ...
''."
*Morris, Robert (1987). ''Composition with Pitch Classes'', p. 167. New Haven and London: Yale University Press. . Discusses automorphisms.
References
{{reflist Post-tonal music theory