Historians of mathematics on:
[Wikipedia]
[Google]
[Amazon]
 The history of mathematics deals with the origin of discoveries in
The history of mathematics deals with the origin of discoveries in
 In contrast to the sparsity of sources in
In contrast to the sparsity of sources in

 Greek mathematics refers to the mathematics written in the
Greek mathematics refers to the mathematics written in the  In the 3rd century BC, the premier center of mathematical education and research was the
In the 3rd century BC, the premier center of mathematical education and research was the 

 Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics. During this period,
Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics. During this period,  Among the last great Greek mathematicians is
Among the last great Greek mathematicians is
 Although
Although
 An analysis of early Chinese mathematics has demonstrated its unique development compared to other parts of the world, leading scholars to assume an entirely independent development. The oldest extant mathematical text from China is the ''
An analysis of early Chinese mathematics has demonstrated its unique development compared to other parts of the world, leading scholars to assume an entirely independent development. The oldest extant mathematical text from China is the '' Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called "rod numerals" in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten. Thus, the number 123 would be written using the symbol for "1", followed by the symbol for "100", then the symbol for "2" followed by the symbol for "10", followed by the symbol for "3". This was the most advanced number system in the world at the time, apparently in use several centuries before the common era and well before the development of the Indian numeral system.
Of particular note is the use in Chinese mathematics of a decimal positional notation system, the so-called "rod numerals" in which distinct ciphers were used for numbers between 1 and 10, and additional ciphers for powers of ten. Thus, the number 123 would be written using the symbol for "1", followed by the symbol for "100", then the symbol for "2" followed by the symbol for "10", followed by the symbol for "3". This was the most advanced number system in the world at the time, apparently in use several centuries before the common era and well before the development of the Indian numeral system.  In 212 BC, the Emperor
In 212 BC, the Emperor
 The earliest civilization on the Indian subcontinent is the Indus Valley civilization (mature phase: 2600 to 1900 BC) that flourished in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a squaring the circle, circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the
The earliest civilization on the Indian subcontinent is the Indus Valley civilization (mature phase: 2600 to 1900 BC) that flourished in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a squaring the circle, circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the
 The Caliphate, Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberian Peninsula, Iberia, and in parts of History of India, India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic language, Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persian people, Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian people, Persian mathematician
The Caliphate, Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberian Peninsula, Iberia, and in parts of History of India, India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic language, Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persian people, Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian people, Persian mathematician
 In the Pre-Columbian Americas, the
In the Pre-Columbian Americas, the
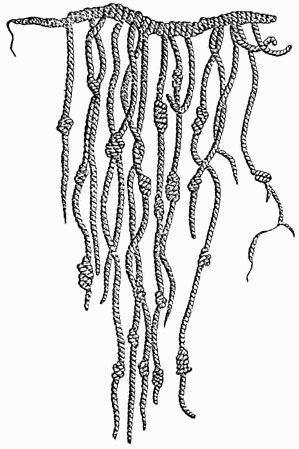 The prevailing numeral system was the Decimal, base-ten.
In precolumbian americas the Inca empire had made various accomplishment in mathematical field.The Incas used their own numeral system which has the base ten.
It is also confirmed that the Incas use of the decimal system by the interpretation of the quipus, which are organized in such a way that the knots — according to their location — can represent: units, tens, hundreds, etc.
However, the main confirmation of the use of this system is expressed in the denomination of the numbers in Quechuan languages, Quechua, in which the numbers are developed in decimal form. This can be appreciated in the following table:
The prevailing numeral system was the Decimal, base-ten.
In precolumbian americas the Inca empire had made various accomplishment in mathematical field.The Incas used their own numeral system which has the base ten.
It is also confirmed that the Incas use of the decimal system by the interpretation of the quipus, which are organized in such a way that the knots — according to their location — can represent: units, tens, hundreds, etc.
However, the main confirmation of the use of this system is expressed in the denomination of the numbers in Quechuan languages, Quechua, in which the numbers are developed in decimal form. This can be appreciated in the following table:
 Most of the mathematics in Japan had either imported from China although many of the mathematical accomplishment was also made by Japanese mathematicans.
One prominent mathematician during Edo period was Seki Takakazu. He created a new algebraic notation system and, motivated by astronomical computations, did work on infinitesimal calculus and Diophantine equations.
He had a significant impact on
Most of the mathematics in Japan had either imported from China although many of the mathematical accomplishment was also made by Japanese mathematicans.
One prominent mathematician during Edo period was Seki Takakazu. He created a new algebraic notation system and, motivated by astronomical computations, did work on infinitesimal calculus and Diophantine equations.
He had a significant impact on
/ref> He obtained power series expansion of in 1722, 15 years earlier than Euler. He used Richardson extrapolation in 1695, about 200 years earlier than Richardson. He also computed 41 digits of π, based on polygon approximation and Richardson extrapolation. Ajima Naonobu was credited for introducing
 One of the 14th-century Oxford Calculators, William Heytesbury, lacking differential calculus and the concept of Limit of a function, limits, proposed to measure instantaneous speed "by the path that would be described by [a body] if... it were moved uniformly at the same degree of speed with which it is moved in that given instant".
Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by
One of the 14th-century Oxford Calculators, William Heytesbury, lacking differential calculus and the concept of Limit of a function, limits, proposed to measure instantaneous speed "by the path that would be described by [a body] if... it were moved uniformly at the same degree of speed with which it is moved in that given instant".
Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by
 The 17th century saw an unprecedented increase of mathematical and scientific ideas across Europe. Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. By his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion.
The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.
Building on earlier work by many predecessors,
The 17th century saw an unprecedented increase of mathematical and scientific ideas across Europe. Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. By his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion.
The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.
Building on earlier work by many predecessors,
 The most influential mathematician of the 18th century was arguably Leonhard Euler (1707–1783). His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol Imaginary unit, ''i'', and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
The most influential mathematician of the 18th century was arguably Leonhard Euler (1707–1783). His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol Imaginary unit, ''i'', and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
 Differential geometry came into its own when Albert Einstein used it in general relativity. Entirely new areas of mathematics such as mathematical logic, topology, and John von Neumann's game theory changed the kinds of questions that could be answered by mathematical methods. All kinds of Mathematical structure, structures were abstracted using axioms and given names like metric spaces, topological spaces etc. As mathematicians do, the concept of an abstract structure was itself abstracted and led to category theory. Grothendieck and Jean-Pierre Serre, Serre recast algebraic geometry using Sheaf (mathematics), sheaf theory. Large advances were made in the qualitative study of dynamical systems theory, dynamical systems that Henri Poincaré, Poincaré had begun in the 1890s.
Measure theory was developed in the late 19th and early 20th centuries. Applications of measures include the Lebesgue integral, Kolmogorov's axiomatisation of probability theory, and ergodic theory. Knot theory greatly expanded. Quantum mechanics led to the development of functional analysis. Other new areas include Laurent Schwartz's Distribution (mathematics), distribution theory, Fixed-point theorem, fixed point theory, singularity theory and René Thom's catastrophe theory, model theory, and Benoit Mandelbrot, Mandelbrot's fractals. Lie theory with its Lie groups and Lie algebras became one of the major areas of study.
Non-standard analysis, introduced by Abraham Robinson, rehabilitated the infinitesimal approach to calculus, which had fallen into disrepute in favour of the theory of Limit of a function, limits, by extending the field of real numbers to the Hyperreal numbers which include infinitesimal and infinite quantities. An even larger number system, the surreal numbers were discovered by John Horton Conway in connection with combinatorial games.
The development and continual improvement of computers, at first mechanical analog machines and then digital electronic machines, allowed Private industry, industry to deal with larger and larger amounts of data to facilitate mass production and distribution and communication, and new areas of mathematics were developed to deal with this: Alan Turing's computability theory; Computational complexity theory, complexity theory; Derrick Henry Lehmer's use of ENIAC to further number theory and the Lucas-Lehmer test; Rózsa Péter's recursive function theory; Claude Shannon's information theory; signal processing; data analysis; Mathematical optimization, optimization and other areas of operations research. In the preceding centuries much mathematical focus was on
Differential geometry came into its own when Albert Einstein used it in general relativity. Entirely new areas of mathematics such as mathematical logic, topology, and John von Neumann's game theory changed the kinds of questions that could be answered by mathematical methods. All kinds of Mathematical structure, structures were abstracted using axioms and given names like metric spaces, topological spaces etc. As mathematicians do, the concept of an abstract structure was itself abstracted and led to category theory. Grothendieck and Jean-Pierre Serre, Serre recast algebraic geometry using Sheaf (mathematics), sheaf theory. Large advances were made in the qualitative study of dynamical systems theory, dynamical systems that Henri Poincaré, Poincaré had begun in the 1890s.
Measure theory was developed in the late 19th and early 20th centuries. Applications of measures include the Lebesgue integral, Kolmogorov's axiomatisation of probability theory, and ergodic theory. Knot theory greatly expanded. Quantum mechanics led to the development of functional analysis. Other new areas include Laurent Schwartz's Distribution (mathematics), distribution theory, Fixed-point theorem, fixed point theory, singularity theory and René Thom's catastrophe theory, model theory, and Benoit Mandelbrot, Mandelbrot's fractals. Lie theory with its Lie groups and Lie algebras became one of the major areas of study.
Non-standard analysis, introduced by Abraham Robinson, rehabilitated the infinitesimal approach to calculus, which had fallen into disrepute in favour of the theory of Limit of a function, limits, by extending the field of real numbers to the Hyperreal numbers which include infinitesimal and infinite quantities. An even larger number system, the surreal numbers were discovered by John Horton Conway in connection with combinatorial games.
The development and continual improvement of computers, at first mechanical analog machines and then digital electronic machines, allowed Private industry, industry to deal with larger and larger amounts of data to facilitate mass production and distribution and communication, and new areas of mathematics were developed to deal with this: Alan Turing's computability theory; Computational complexity theory, complexity theory; Derrick Henry Lehmer's use of ENIAC to further number theory and the Lucas-Lehmer test; Rózsa Péter's recursive function theory; Claude Shannon's information theory; signal processing; data analysis; Mathematical optimization, optimization and other areas of operations research. In the preceding centuries much mathematical focus was on
Renaissance Mathematics
BBC Radio 4 discussion with Robert Kaplan, Jim Bennett & Jackie Stedall (''In Our Time'', Jun 2, 2005)
MacTutor History of Mathematics archive
(John J. O'Connor and Edmund F. Robertson; University of St Andrews, Scotland). An award-winning website containing detailed biographies on many historical and contemporary mathematicians, as well as information on notable curves and various topics in the history of mathematics.
History of Mathematics Home Page
(David E. Joyce; Clark University). Articles on various topics in the history of mathematics with an extensive bibliography.
The History of Mathematics
(David R. Wilkins; Trinity College, Dublin). Collections of material on the mathematics between the 17th and 19th century.
(Jeff Miller). Contains information on the earliest known uses of terms used in mathematics.
(Jeff Miller). Contains information on the history of mathematical notations.
(John Aldrich, University of Southampton) Discusses the origins of the modern mathematical word stock.
(Larry Riddle; Agnes Scott College).
Mathematicians of the African Diaspora
(Scott W. Williams; University at Buffalo).
Notes for MAA minicourse: teaching a course in the history of mathematics. (2009)
(V. Frederick Rickey & Victor J. Katz).
Ancient Rome: The Odometer Of Vitruv
Pictorial (moving) re-construction of Vitusius' Roman ododmeter.
A Bibliography of Collected Works and Correspondence of Mathematiciansarchive dated 2007/3/17
(Steven W. Rockey; Cornell University Library).
International Commission for the History of Mathematics
Convergence
the Mathematical Association of America's online ''Math History'' Magazine
History of Mathematics
Math Archives (University of Tennessee, Knoxville)
History/Biography
The Math Forum (Drexel University)
(Courtright Memorial Library).
(David Calvis; Baldwin-Wallace College) *
Historia de las Matemáticas
(Universidad de La La guna)
(Universidade de Coimbra)
Using History in Math Class
(Bruno Kevius)
(Roberta Tucci) {{History of science History of mathematics, History of science by discipline, Mathematics
 The history of mathematics deals with the origin of discoveries in
The history of mathematics deals with the origin of discoveries in mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
and the mathematical methods and notation of the past. Before the modern age
The term modern period or modern era (sometimes also called modern history or modern times) is the period of history that succeeds the Middle Ages (which ended approximately 1500 AD). This terminology is a historical periodization that is applie ...
and the worldwide spread of knowledge, written examples of new mathematical developments have come to light only in a few locales. From 3000 BC the Mesopotamian
Mesopotamia ''Mesopotamíā''; ar, بِلَاد ٱلرَّافِدَيْن or ; syc, ܐܪܡ ܢܗܪ̈ܝܢ, or , ) is a historical region of Western Asia situated within the Tigris–Euphrates river system, in the northern part of the F ...
states of Sumer
Sumer () is the earliest known civilization in the historical region of southern Mesopotamia (south-central Iraq), emerging during the Chalcolithic and early Bronze Ages between the sixth and fifth millennium BC. It is one of the cradles of c ...
, Akkad Akkad may refer to:
*Akkad (city), the capital of the Akkadian Empire
*Akkadian Empire, the first ancient empire of Mesopotamia
*Akkad SC, Iraqi football club
People with the name
*Abbas el-Akkad, Egyptian writer
*Abdulrahman Akkad, Syrian LGBT act ...
and Assyria
Assyria (Neo-Assyrian cuneiform: , romanized: ''māt Aššur''; syc, ܐܬܘܪ, ʾāthor) was a major ancient Mesopotamian civilization which existed as a city-state at times controlling regional territories in the indigenous lands of the A ...
, followed closely by Ancient Egypt and the Levantine state of Ebla
Ebla ( Sumerian: ''eb₂-la'', ar, إبلا, modern: , Tell Mardikh) was one of the earliest kingdoms in Syria. Its remains constitute a tell located about southwest of Aleppo near the village of Mardikh. Ebla was an important center t ...
began using arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
, algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
and geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
for purposes of taxation, commerce, trade and also in the patterns in nature
Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foa ...
, the field of astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest ...
and to record time and formulate calendars
A calendar is a system of organizing days. This is done by giving names to periods of time, typically days, weeks, months and years. A date is the designation of a single and specific day within such a system. A calendar is also a physi ...
.
The earliest mathematical texts available are from Mesopotamia
Mesopotamia ''Mesopotamíā''; ar, بِلَاد ٱلرَّافِدَيْن or ; syc, ܐܪܡ ܢܗܪ̈ܝܢ, or , ) is a historical region of Western Asia situated within the Tigris–Euphrates river system, in the northern part of the F ...
and Egypt
Egypt ( ar, مصر , ), officially the Arab Republic of Egypt, is a transcontinental country spanning the northeast corner of Africa and southwest corner of Asia via a land bridge formed by the Sinai Peninsula. It is bordered by the Mediter ...
– ''Plimpton 322
Plimpton 322 is a Babylonian clay tablet, notable as containing an example of Babylonian mathematics. It has number 322 in the G.A. Plimpton Collection at Columbia University. This tablet, believed to have been written about 1800 BC, has a table ...
'' ( Babylonian c. 2000 – 1900 BC), the '' Rhind Mathematical Papyrus'' (Egyptian
Egyptian describes something of, from, or related to Egypt.
Egyptian or Egyptians may refer to:
Nations and ethnic groups
* Egyptians, a national group in North Africa
** Egyptian culture, a complex and stable culture with thousands of years of ...
c. 1800 BC) and the ''Moscow Mathematical Papyrus
The Moscow Mathematical Papyrus, also named the Golenishchev Mathematical Papyrus after its first non-Egyptian owner, Egyptologist Vladimir Golenishchev, is an ancient Egyptian mathematical papyrus containing several problems in arithmetic, geom ...
'' (Egyptian c. 1890 BC). All of these texts mention the so-called Pythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is ...
s, so, by inference, the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
seems to be the most ancient and widespread mathematical development after basic arithmetic and geometry.
The study of mathematics as a "demonstrative discipline" began in the 6th century BC with the Pythagoreans
Pythagoreanism originated in the 6th century BC, based on and around the teachings and beliefs held by Pythagoras and his followers, the Pythagoreans. Pythagoras established the first Pythagorean community in the ancient Greek colony of Kroton, ...
, who coined the term "mathematics" from the ancient Greek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
''μάθημα'' (''mathema''), meaning "subject of instruction". Greek mathematics
Greek mathematics refers to mathematics texts and ideas stemming from the Archaic through the Hellenistic and Roman periods, mostly extant from the 7th century BC to the 4th century AD, around the shores of the Eastern Mediterranean. Greek mathem ...
greatly refined the methods (especially through the introduction of deductive reasoning and mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
in proofs
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
) and expanded the subject matter of mathematics. Although they made virtually no contributions to theoretical mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications ...
, the ancient Romans
In modern historiography, ancient Rome refers to Roman people, Roman civilisation from the founding of the city of Rome in the 8th century BC to the collapse of the Western Roman Empire in the 5th century AD. It encompasses the Roman Kingdom ...
used applied mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical s ...
in surveying
Surveying or land surveying is the technique, profession, art, and science of determining the terrestrial two-dimensional or three-dimensional positions of points and the distances and angles between them. A land surveying professional is ca ...
, structural engineering
Structural engineering is a sub-discipline of civil engineering in which structural engineers are trained to design the 'bones and muscles' that create the form and shape of man-made structures. Structural engineers also must understand and cal ...
, mechanical engineering
Mechanical engineering is the study of physical machines that may involve force and movement. It is an engineering branch that combines engineering physics and mathematics principles with materials science, to design, analyze, manufacture, and ...
, bookkeeping
Bookkeeping is the recording of financial transactions, and is part of the process of accounting in business and other organizations. It involves preparing source documents for all transactions, operations, and other events of a business. Tr ...
, creation of lunar
Lunar most commonly means "of or relating to the Moon".
Lunar may also refer to:
Arts and entertainment
* ''Lunar'' (series), a series of video games
* "Lunar" (song), by David Guetta
* "Lunar", a song by Priestess from the 2009 album ''Prior t ...
and solar calendar
A solar calendar is a calendar whose dates indicate the season or almost equivalently the apparent position of the Sun relative to the stars. The Gregorian calendar, widely accepted as a standard in the world, is an example of a solar calendar.
T ...
s, and even arts and crafts
A handicraft, sometimes more precisely expressed as artisanal handicraft or handmade, is any of a wide variety of types of work where useful and decorative objects are made completely by one’s hand or by using only simple, non-automated re ...
. Chinese mathematics
Mathematics in China emerged independently by the 11th century BCE. The Chinese independently developed a real number system that includes significantly large and negative numbers, more than one numeral system ( base 2 and base 10), algebra, geomet ...
made early contributions, including a place value system
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the ...
and the first use of negative numbers
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is less than zero. Negative numbers are often used to represent the magnitude of a loss or deficiency. A debt that is owed ma ...
. The Hindu–Arabic numeral system
The Hindu–Arabic numeral system or Indo-Arabic numeral system Audun HolmeGeometry: Our Cultural Heritage 2000 (also called the Hindu numeral system or Arabic numeral system) is a positional decimal numeral system, and is the most common syste ...
and the rules for the use of its operations, in use throughout the world today evolved over the course of the first millennium AD in India
India, officially the Republic of India (Hindi: ), is a country in South Asia. It is the seventh-largest country by area, the second-most populous country, and the most populous democracy in the world. Bounded by the Indian Ocean on the so ...
and were transmitted to the Western world
The Western world, also known as the West, primarily refers to the various nations and state (polity), states in the regions of Europe, North America, and Oceania.
via Islamic mathematics
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full ...
through the work of Muḥammad ibn Mūsā al-Khwārizmī
Muhammad ( ar, مُحَمَّد; 570 – 8 June 632 CE) was an Arab religious, social, and political leader and the founder of Islam. According to Islamic doctrine, he was a prophet divinely inspired to preach and confirm the mono ...
. Islamic mathematics, in turn, developed and expanded the mathematics known to these civilizations. Contemporaneous with but independent of these traditions were the mathematics developed by the Maya civilization
The Maya civilization () of the Mesoamerican people is known by its ancient temples and glyphs. Its Maya script is the most sophisticated and highly developed writing system in the pre-Columbian Americas. It is also noted for its art, archit ...
of Mexico
Mexico (Spanish: México), officially the United Mexican States, is a country in the southern portion of North America. It is bordered to the north by the United States; to the south and west by the Pacific Ocean; to the southeast by Guatema ...
and Central America
Central America ( es, América Central or ) is a subregion of the Americas. Its boundaries are defined as bordering the United States to the north, Colombia to the south, the Caribbean Sea to the east, and the Pacific Ocean to the west. ...
, where the concept of zero
0 (zero) is a number representing an empty quantity. In place-value notation
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or ...
was given a standard symbol in Maya numerals
The Mayan numeral system was the system to represent numbers and calendar dates in the Maya civilization. It was a vigesimal (base-20) positional numeral system. The numerals are made up of three symbols; zero (a shell), one (a dot) and fiv ...
.
Many Greek and Arabic texts on mathematics were translated into Latin from the 12th century onward, leading to further development of mathematics in Medieval Europe
In the history of Europe, the Middle Ages or medieval period lasted approximately from the late 5th to the late 15th centuries, similar to the post-classical period of global history. It began with the fall of the Western Roman Empire a ...
. From ancient times through the Middle Ages
In the history of Europe, the Middle Ages or medieval period lasted approximately from the late 5th to the late 15th centuries, similar to the post-classical period of global history. It began with the fall of the Western Roman Empire a ...
, periods of mathematical discovery were often followed by centuries of stagnation. Beginning in Renaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas ...
Italy
Italy ( it, Italia ), officially the Italian Republic, ) or the Republic of Italy, is a country in Southern Europe. It is located in the middle of the Mediterranean Sea, and its territory largely coincides with the homonymous geographical re ...
in the 15th century, new mathematical developments, interacting with new scientific discoveries, were made at an increasing pace that continues through the present day. This includes the groundbreaking work of both Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the grea ...
and Gottfried Wilhelm Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathema ...
in the development of infinitesimal calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
during the course of the 17th century.
Prehistoric
The origins of mathematical thought lie in the concepts ofnumber
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers c ...
, patterns in nature
Patterns in nature are visible regularities of form found in the natural world. These patterns recur in different contexts and can sometimes be modelled mathematically. Natural patterns include symmetries, trees, spirals, meanders, waves, foa ...
, magnitude
Magnitude may refer to:
Mathematics
*Euclidean vector, a quantity defined by both its magnitude and its direction
*Magnitude (mathematics), the relative size of an object
*Norm (mathematics), a term for the size or length of a vector
*Order of ...
, and form
Form is the shape, visual appearance, or configuration of an object. In a wider sense, the form is the way something happens.
Form also refers to:
*Form (document), a document (printed or electronic) with spaces in which to write or enter data
...
. Modern studies of animal cognition have shown that these concepts are not unique to humans. Such concepts would have been part of everyday life in hunter-gatherer societies. The idea of the "number" concept evolving gradually over time is supported by the existence of languages which preserve the distinction between "one", "two", and "many", but not of numbers larger than two.
The Ishango bone
The Ishango bone, discovered at the "Fisherman Settlement" of Ishango in the Democratic Republic of Congo, is a bone tool and possible mathematical device that dates to the Upper Paleolithic era. The curved bone is dark brown in color, about 10 ce ...
, found near the headwaters of the Nile
The Nile, , Bohairic , lg, Kiira , Nobiin language, Nobiin: Áman Dawū is a major north-flowing river in northeastern Africa. It flows into the Mediterranean Sea. The Nile is the longest river in Africa and has historically been considered ...
river (northeastern Congo), may be more than 20,000 years old and consists of a series of marks carved in three columns running the length of the bone. Common interpretations are that the Ishango bone shows either a ''tally'' of the earliest known demonstration of sequence
In mathematics, a sequence is an enumerated collection of objects in which repetitions are allowed and order matters. Like a set, it contains members (also called ''elements'', or ''terms''). The number of elements (possibly infinite) is calle ...
s of prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s or a six-month lunar calendar.Marshack, Alexander (1991): ''The Roots of Civilization'', Colonial Hill, Mount Kisco, NY. Peter Rudman argues that the development of the concept of prime numbers could only have come about after the concept of division, which he dates to after 10,000 BC, with prime numbers probably not being understood until about 500 BC. He also writes that "no attempt has been made to explain why a tally of something should exhibit multiples of two, prime numbers between 10 and 20, and some numbers that are almost multiples of 10." The Ishango bone, according to scholar Alexander Marshack Alexander Marshack (April 4, 1918 – December 20, 2004) was an American independent scholar and Paleolithic archaeologist. He was born in The Bronx and earned a bachelor's degree in journalism from City College of New York, and worked for many y ...
, may have influenced the later development of mathematics in Egypt as, like some entries on the Ishango bone, Egyptian arithmetic also made use of multiplication by 2; this however, is disputed.
Predynastic Egypt
Prehistoric Egypt and Predynastic Egypt span the period from the earliest human settlement to the beginning of the Early Dynastic Period around 3100 BC, starting with the first Pharaoh, Narmer for some Egyptologists, Hor-Aha for others, with th ...
ians of the 5th millennium BC pictorially represented geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
designs. It has been claimed that megalith
A megalith is a large stone that has been used to construct a prehistoric structure or monument, either alone or together with other stones. There are over 35,000 in Europe alone, located widely from Sweden to the Mediterranean sea.
The ...
ic monuments in England
England is a country that is part of the United Kingdom. It shares land borders with Wales to its west and Scotland to its north. The Irish Sea lies northwest and the Celtic Sea to the southwest. It is separated from continental Europe b ...
and Scotland
Scotland (, ) is a country that is part of the United Kingdom. Covering the northern third of the island of Great Britain, mainland Scotland has a border with England to the southeast and is otherwise surrounded by the Atlantic Ocean to the ...
, dating from the 3rd millennium BC, incorporate geometric ideas such as circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
s, ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
s, and Pythagorean triple
A Pythagorean triple consists of three positive integers , , and , such that . Such a triple is commonly written , and a well-known example is . If is a Pythagorean triple, then so is for any positive integer . A primitive Pythagorean triple is ...
s in their design. All of the above are disputed however, and the currently oldest undisputed mathematical documents are from Babylonian and dynastic Egyptian sources.
Babylonian
Babylonia
Babylonia (; Akkadian: , ''māt Akkadī'') was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Syria). It emerged as an Amorite-ruled state c. ...
n mathematics refers to any mathematics of the peoples of Mesopotamia
Mesopotamia ''Mesopotamíā''; ar, بِلَاد ٱلرَّافِدَيْن or ; syc, ܐܪܡ ܢܗܪ̈ܝܢ, or , ) is a historical region of Western Asia situated within the Tigris–Euphrates river system, in the northern part of the F ...
(modern Iraq
Iraq,; ku, عێراق, translit=Êraq officially the Republic of Iraq, '; ku, کۆماری عێراق, translit=Komarî Êraq is a country in Western Asia. It is bordered by Turkey to Iraq–Turkey border, the north, Iran to Iran–Iraq ...
) from the days of the early Sumer
Sumer () is the earliest known civilization in the historical region of southern Mesopotamia (south-central Iraq), emerging during the Chalcolithic and early Bronze Ages between the sixth and fifth millennium BC. It is one of the cradles of c ...
ians through the Hellenistic period
In Classical antiquity, the Hellenistic period covers the time in Mediterranean history after Classical Greece, between the death of Alexander the Great in 323 BC and the emergence of the Roman Empire, as signified by the Battle of Actium in 3 ...
almost to the dawn of Christianity
Christianity is an Abrahamic monotheistic religion based on the life and teachings of Jesus of Nazareth. It is the world's largest and most widespread religion with roughly 2.38 billion followers representing one-third of the global pop ...
. The majority of Babylonian mathematical work comes from two widely separated periods: The first few hundred years of the second millennium BC (Old Babylonian period), and the last few centuries of the first millennium BC (Seleucid
The Seleucid Empire (; grc, Βασιλεία τῶν Σελευκιδῶν, ''Basileía tōn Seleukidōn'') was a Greek state in West Asia that existed during the Hellenistic period from 312 BC to 63 BC. The Seleucid Empire was founded by the ...
period). It is named Babylonian mathematics due to the central role of Babylon
''Bābili(m)''
* sux, 𒆍𒀭𒊏𒆠
* arc, 𐡁𐡁𐡋 ''Bāḇel''
* syc, ܒܒܠ ''Bāḇel''
* grc-gre, Βαβυλών ''Babylṓn''
* he, בָּבֶל ''Bāvel''
* peo, 𐎲𐎠𐎲𐎡𐎽𐎢 ''Bābiru''
* elx, 𒀸𒁀𒉿𒇷 ''Babi ...
as a place of study. Later under the Arab Empire, Mesopotamia, especially Baghdad
Baghdad (; ar, بَغْدَاد , ) is the capital of Iraq and the second-largest city in the Arab world after Cairo. It is located on the Tigris near the ruins of the ancient city of Babylon and the Sassanid Persian capital of Ctesiphon ...
, once again became an important center of study for Islamic mathematics
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full ...
.
 In contrast to the sparsity of sources in
In contrast to the sparsity of sources in Egyptian mathematics
Ancient Egyptian mathematics is the mathematics that was developed and used in Ancient Egypt 3000 to c. , from the Old Kingdom of Egypt until roughly the beginning of Hellenistic Egypt. The ancient Egyptians utilized a numeral system for count ...
, knowledge of Babylonian mathematics is derived from more than 400 clay tablets unearthed since the 1850s. Written in Cuneiform script
Cuneiform is a logo-syllabic script that was used to write several languages of the Ancient Middle East. The script was in active use from the early Bronze Age until the beginning of the Common Era. It is named for the characteristic wedge-sha ...
, tablets were inscribed whilst the clay was moist, and baked hard in an oven or by the heat of the sun. Some of these appear to be graded homework.
The earliest evidence of written mathematics dates back to the ancient Sumer
Sumer () is the earliest known civilization in the historical region of southern Mesopotamia (south-central Iraq), emerging during the Chalcolithic and early Bronze Ages between the sixth and fifth millennium BC. It is one of the cradles of c ...
ians, who built the earliest civilization in Mesopotamia. They developed a complex system of metrology
Metrology is the scientific study of measurement. It establishes a common understanding of units, crucial in linking human activities. Modern metrology has its roots in the French Revolution's political motivation to standardise units in Fran ...
from 3000 BC. From around 2500 BC onward, the Sumerians wrote multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essenti ...
s on clay tablets and dealt with geometrical
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
exercises and division
Division or divider may refer to:
Mathematics
*Division (mathematics), the inverse of multiplication
*Division algorithm, a method for computing the result of mathematical division
Military
*Division (military), a formation typically consisting ...
problems. The earliest traces of the Babylonian numerals also date back to this period.
Babylonian mathematics were written using a sexagesimal
Sexagesimal, also known as base 60 or sexagenary, is a numeral system with sixty as its base. It originated with the ancient Sumerians in the 3rd millennium BC, was passed down to the ancient Babylonians, and is still used—in a modified form� ...
(base-60) numeral system
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using Numerical digit, digits or other symbols in a consistent manner.
The same s ...
. From this derives the modern-day usage of 60 seconds in a minute, 60 minutes in an hour, and 360 (60 × 6) degrees in a circle, as well as the use of seconds and minutes of arc to denote fractions of a degree. It is likely the sexagesimal system was chosen because 60 can be evenly divided by 2, 3, 4, 5, 6, 10, 12, 15, 20 and 30. Also, unlike the Egyptians, Greeks, and Romans, the Babylonians had a place-value system, where digits written in the left column represented larger values, much as in the decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
system. The power of the Babylonian notational system lay in that it could be used to represent fractions as easily as whole numbers; thus multiplying two numbers that contained fractions was no different from multiplying integers, similar to modern notation. The notational system of the Babylonians was the best of any civilization until the Renaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas ...
, and its power allowed it to achieve remarkable computational accuracy; for example, the Babylonian tablet YBC 7289
YBC 7289 is a Babylonian clay tablet notable for containing an accurate sexagesimal approximation to the square root of 2, the length of the diagonal of a unit square. This number is given to the equivalent of six decimal digits, "the greatest ...
gives an approximation of accurate to five decimal places. The Babylonians lacked, however, an equivalent of the decimal point, and so the place value of a symbol often had to be inferred from the context. By the Seleucid period, the Babylonians had developed a zero symbol as a placeholder for empty positions; however it was only used for intermediate positions. This zero sign does not appear in terminal positions, thus the Babylonians came close but did not develop a true place value system.
Other topics covered by Babylonian mathematics include fractions, algebra, quadratic and cubic equations, and the calculation of regular number
Regular numbers are numbers that evenly divide powers of 60 (or, equivalently, powers of 30). Equivalently, they are the numbers whose only prime divisors are 2, 3, and 5. As an example, 602 = 3600 = 48 ×&nb ...
s, and their reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
pairs
Concentration, also known as Memory, Shinkei-suijaku (Japanese meaning "nervous breakdown"), Matching Pairs, Match Match, Match Up, Pelmanism, Pexeso or simply Pairs, is a card game in which all of the cards are laid face down on a surface and tw ...
. The tablets also include multiplication tables and methods for solving linear
Linearity is the property of a mathematical relationship (''function'') that can be graphically represented as a straight line. Linearity is closely related to '' proportionality''. Examples in physics include rectilinear motion, the linear r ...
, quadratic equation
In algebra, a quadratic equation () is any equation that can be rearranged in standard form as
ax^2 + bx + c = 0\,,
where represents an unknown (mathematics), unknown value, and , , and represent known numbers, where . (If and then the equati ...
s and cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s, a remarkable achievement for the time. Tablets from the Old Babylonian period also contain the earliest known statement of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
. However, as with Egyptian mathematics, Babylonian mathematics shows no awareness of the difference between exact and approximate solutions, or the solvability of a problem, and most importantly, no explicit statement of the need for proofs
Proof most often refers to:
* Proof (truth), argument or sufficient evidence for the truth of a proposition
* Alcohol proof, a measure of an alcoholic drink's strength
Proof may also refer to:
Mathematics and formal logic
* Formal proof, a co ...
or logical principles.
Egyptian

Egypt
Egypt ( ar, مصر , ), officially the Arab Republic of Egypt, is a transcontinental country spanning the northeast corner of Africa and southwest corner of Asia via a land bridge formed by the Sinai Peninsula. It is bordered by the Mediter ...
ian mathematics refers to mathematics written in the Egyptian language
The Egyptian language or Ancient Egyptian ( ) is a dead language, dead Afroasiatic languages, Afro-Asiatic language that was spoken in ancient Egypt. It is known today from a large Text corpus, corpus of surviving texts which were made acces ...
. From the Hellenistic period
In Classical antiquity, the Hellenistic period covers the time in Mediterranean history after Classical Greece, between the death of Alexander the Great in 323 BC and the emergence of the Roman Empire, as signified by the Battle of Actium in 3 ...
, Greek
Greek may refer to:
Greece
Anything of, from, or related to Greece, a country in Southern Europe:
*Greeks, an ethnic group.
*Greek language, a branch of the Indo-European language family.
**Proto-Greek language, the assumed last common ancestor ...
replaced Egyptian as the written language of Egyptian
Egyptian describes something of, from, or related to Egypt.
Egyptian or Egyptians may refer to:
Nations and ethnic groups
* Egyptians, a national group in North Africa
** Egyptian culture, a complex and stable culture with thousands of years of ...
scholars. Mathematical study in Egypt
Egypt ( ar, مصر , ), officially the Arab Republic of Egypt, is a transcontinental country spanning the northeast corner of Africa and southwest corner of Asia via a land bridge formed by the Sinai Peninsula. It is bordered by the Mediter ...
later continued under the Arab Empire as part of Islamic mathematics
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full ...
, when Arabic
Arabic (, ' ; , ' or ) is a Semitic languages, Semitic language spoken primarily across the Arab world.Semitic languages: an international handbook / edited by Stefan Weninger; in collaboration with Geoffrey Khan, Michael P. Streck, Janet C ...
became the written language of Egyptian scholars. Archaeological evidence has suggested that the Ancient Egyptian counting system had origins in Sub-Saharan Africa. Also, fractal geometry designs which are widespread among Sub-Saharan African cultures are also found in Egyptian architecture and cosmological signs.
The most extensive Egyptian mathematical text is the Rhind papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057 and pBM 10058) is one of the best known examples of ancient Egyptian mathematics. It is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased ...
(sometimes also called the Ahmes Papyrus after its author), dated to c. 1650 BC but likely a copy of an older document from the Middle Kingdom of about 2000–1800 BC. It is an instruction manual for students in arithmetic and geometry. In addition to giving area formulas and methods for multiplication, division and working with unit fractions, it also contains evidence of other mathematical knowledge, including composite
Composite or compositing may refer to:
Materials
* Composite material, a material that is made from several different substances
** Metal matrix composite, composed of metal and other parts
** Cermet, a composite of ceramic and metallic materials
...
and prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
s; arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
, geometric
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is ca ...
and harmonic mean
In mathematics, the harmonic mean is one of several kinds of average, and in particular, one of the Pythagorean means. It is sometimes appropriate for situations when the average rate is desired.
The harmonic mean can be expressed as the recipro ...
s; and simplistic understandings of both the Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime n ...
and perfect number theory (namely, that of the number 6). It also shows how to solve first order linear equation
In mathematics, a linear equation is an equation that may be put in the form
a_1x_1+\ldots+a_nx_n+b=0, where x_1,\ldots,x_n are the variables (or unknowns), and b,a_1,\ldots,a_n are the coefficients, which are often real numbers. The coefficien ...
s as well as arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
and geometric series
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
:\frac \,+\, \frac \,+\, \frac \,+\, \frac \,+\, \cdots
is geometric, because each succ ...
.
Another significant Egyptian mathematical text is the Moscow papyrus
The Moscow Mathematical Papyrus, also named the Golenishchev Mathematical Papyrus after its first non-Egyptian owner, Egyptologist Vladimir Golenishchev, is an ancient Egyptian mathematical papyrus containing several problems in arithmetic, geom ...
, also from the Middle Kingdom period, dated to c. 1890 BC. It consists of what are today called ''word problems'' or ''story problems'', which were apparently intended as entertainment. One problem is considered to be of particular importance because it gives a method for finding the volume of a frustum
In geometry, a (from the Latin for "morsel"; plural: ''frusta'' or ''frustums'') is the portion of a solid (normally a pyramid or a cone) that lies between two parallel planes cutting this solid. In the case of a pyramid, the base faces are ...
(truncated pyramid).
Finally, the Berlin Papyrus 6619
The Berlin Papyrus 6619, simply called the Berlin Papyrus when the context makes it clear, is one of the primary sources of ancient Egyptian mathematics. One of the two mathematics problems on the Papyrus may suggest that the ancient Egyptians kn ...
(c. 1800 BC) shows that ancient Egyptians could solve a second-order algebraic equation
In mathematics, an algebraic equation or polynomial equation is an equation of the form
:P = 0
where ''P'' is a polynomial with coefficients in some field, often the field of the rational numbers. For many authors, the term ''algebraic equation'' ...
.
Greek
Greek language
Greek ( el, label=Modern Greek, Ελληνικά, Elliniká, ; grc, Ἑλληνική, Hellēnikḗ) is an independent branch of the Indo-European family of languages, native to Greece, Cyprus, southern Italy (Calabria and Salento), southern Al ...
from the time of Thales of Miletus
Thales of Miletus ( ; grc-gre, Θαλῆς; ) was a Greek mathematician, astronomer, statesman, and pre-Socratic philosopher from Miletus in Ionia, Asia Minor. He was one of the Seven Sages of Greece. Many, most notably Aristotle, regarded him ...
(~600 BC) to the closure of the Academy of Athens in 529 AD. Greek mathematicians lived in cities spread over the entire Eastern Mediterranean, from Italy to North Africa, but were united by culture and language. Greek mathematics of the period following Alexander the Great
Alexander III of Macedon ( grc, wikt:Ἀλέξανδρος, Ἀλέξανδρος, Alexandros; 20/21 July 356 BC – 10/11 June 323 BC), commonly known as Alexander the Great, was a king of the Ancient Greece, ancient Greek kingdom of Maced ...
is sometimes called Hellenistic
In Classical antiquity, the Hellenistic period covers the time in Mediterranean history after Classical Greece, between the death of Alexander the Great in 323 BC and the emergence of the Roman Empire, as signified by the Battle of Actium in ...
mathematics.
Greek mathematics was much more sophisticated than the mathematics that had been developed by earlier cultures. All surviving records of pre-Greek mathematics show the use of inductive reasoning
Inductive reasoning is a method of reasoning in which a general principle is derived from a body of observations. It consists of making broad generalizations based on specific observations. Inductive reasoning is distinct from ''deductive'' re ...
, that is, repeated observations used to establish rules of thumb. Greek mathematicians, by contrast, used deductive reasoning
Deductive reasoning is the mental process of drawing deductive inferences. An inference is deductively valid if its conclusion follows logically from its premises, i.e. if it is impossible for the premises to be true and the conclusion to be fals ...
. The Greeks used logic to derive conclusions from definitions and axioms, and used mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
to prove them.
Greek mathematics is thought to have begun with Thales of Miletus
Thales of Miletus ( ; grc-gre, Θαλῆς; ) was a Greek mathematician, astronomer, statesman, and pre-Socratic philosopher from Miletus in Ionia, Asia Minor. He was one of the Seven Sages of Greece. Many, most notably Aristotle, regarded him ...
(c. 624–c.546 BC) and Pythagoras of Samos
Pythagoras of Samos ( grc, Πυθαγόρας ὁ Σάμιος, Pythagóras ho Sámios, Pythagoras the Samian, or simply ; in Ionian Greek; ) was an ancient Ionian Greek philosopher and the eponymous founder of Pythagoreanism. His polit ...
(c. 582–c. 507 BC). Although the extent of the influence is disputed, they were probably inspired by Egyptian
Egyptian describes something of, from, or related to Egypt.
Egyptian or Egyptians may refer to:
Nations and ethnic groups
* Egyptians, a national group in North Africa
** Egyptian culture, a complex and stable culture with thousands of years of ...
and Babylonian mathematics
Babylonian mathematics (also known as ''Assyro-Babylonian mathematics'') are the mathematics developed or practiced by the people of Mesopotamia, from the days of the early Sumerians to the centuries following the fall of Babylon in 539 BC. Babyl ...
. According to legend, Pythagoras traveled to Egypt to learn mathematics, geometry, and astronomy from Egyptian priests.
Thales used geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
to solve problems such as calculating the height of pyramids
A pyramid (from el, πυραμίς ') is a structure whose outer surfaces are triangular and converge to a single step at the top, making the shape roughly a pyramid in the geometric sense. The base of a pyramid can be trilateral, quadrilate ...
and the distance of ships from the shore. He is credited with the first use of deductive reasoning applied to geometry, by deriving four corollaries to Thales' Theorem
In geometry, Thales's theorem states that if A, B, and C are distinct points on a circle where the line is a diameter, the angle ABC is a right angle. Thales's theorem is a special case of the inscribed angle theorem and is mentioned and proved ...
. As a result, he has been hailed as the first true mathematician and the first known individual to whom a mathematical discovery has been attributed. Pythagoras established the Pythagorean School, whose doctrine it was that mathematics ruled the universe and whose motto was "All is number". It was the Pythagoreans who coined the term "mathematics", and with whom the study of mathematics for its own sake begins. The Pythagoreans are credited with the first proof of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, though the statement of the theorem has a long history, and with the proof of the existence of irrational numbers
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two inte ...
. Although he was preceded by the Babylonians
Babylonia (; Akkadian: , ''māt Akkadī'') was an ancient Akkadian-speaking state and cultural area based in the city of Babylon in central-southern Mesopotamia (present-day Iraq and parts of Syria). It emerged as an Amorite-ruled state c. ...
, Indians and the Chinese
Chinese can refer to:
* Something related to China
* Chinese people, people of Chinese nationality, citizenship, and/or ethnicity
**''Zhonghua minzu'', the supra-ethnic concept of the Chinese nation
** List of ethnic groups in China, people of ...
, the Neopythagorean
Neopythagoreanism (or neo-Pythagoreanism) was a school of Hellenistic philosophy which revived Pythagorean doctrines. Neopythagoreanism was influenced by middle Platonism and in turn influenced Neoplatonism. It originated in the 1st century BC a ...
mathematician Nicomachus
Nicomachus of Gerasa ( grc-gre, Νικόμαχος; c. 60 – c. 120 AD) was an important ancient mathematician and music theorist, best known for his works ''Introduction to Arithmetic'' and ''Manual of Harmonics'' in Greek. He was born in ...
(60–120 AD) provided one of the earliest Greco-Roman
The Greco-Roman civilization (; also Greco-Roman culture; spelled Graeco-Roman in the Commonwealth), as understood by modern scholars and writers, includes the geographical regions and countries that culturally—and so historically—were di ...
multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essenti ...
s, whereas the oldest extant Greek multiplication table is found on a wax tablet dated to the 1st century AD (now found in the British Museum
The British Museum is a public museum dedicated to human history, art and culture located in the Bloomsbury area of London. Its permanent collection of eight million works is among the largest and most comprehensive in existence. It docum ...
). The association of the Neopythagoreans with the Western invention of the multiplication table is evident in its later Medieval
In the history of Europe, the Middle Ages or medieval period lasted approximately from the late 5th to the late 15th centuries, similar to the Post-classical, post-classical period of World history (field), global history. It began with t ...
name: the ''mensa Pythagorica''.
Plato
Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution ...
(428/427 BC – 348/347 BC) is important in the history of mathematics for inspiring and guiding others. His Platonic Academy
The Academy (Ancient Greek: Ἀκαδημία) was founded by Plato in c. 387 BC in Classical Athens, Athens. Aristotle studied there for twenty years (367–347 BC) before founding his own school, the Lyceum (classical), Lyceum. The Academy ...
, in Athens
Athens ( ; el, Αθήνα, Athína ; grc, Ἀθῆναι, Athênai (pl.) ) is both the capital and largest city of Greece. With a population close to four million, it is also the seventh largest city in the European Union. Athens dominates ...
, became the mathematical center of the world in the 4th century BC, and it was from this school that the leading mathematicians of the day, such as Eudoxus of Cnidus
Eudoxus of Cnidus (; grc, Εὔδοξος ὁ Κνίδιος, ''Eúdoxos ho Knídios''; ) was an ancient Greek astronomer, mathematician, scholar, and student of Archytas and Plato. All of his original works are lost, though some fragments are ...
, came. Plato also discussed the foundations of mathematics, clarified some of the definitions (e.g. that of a line as "breadthless length"), and reorganized the assumptions. The analytic method is ascribed to Plato, while a formula for obtaining Pythagorean triples bears his name.
Eudoxus (408–c. 355 BC) developed the method of exhaustion
The method of exhaustion (; ) is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area bet ...
, a precursor of modern integration
Integration may refer to:
Biology
*Multisensory integration
*Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technology, ...
and a theory of ratios that avoided the problem of incommensurable magnitudes. The former allowed the calculations of areas and volumes of curvilinear figures, while the latter enabled subsequent geometers to make significant advances in geometry. Though he made no specific technical mathematical discoveries, Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatetic school of phil ...
(384–c. 322 BC) contributed significantly to the development of mathematics by laying the foundations of logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises ...
.
 In the 3rd century BC, the premier center of mathematical education and research was the
In the 3rd century BC, the premier center of mathematical education and research was the Musaeum
The Musaeum or Mouseion of Alexandria ( grc, Μουσεῖον τῆς Ἀλεξανδρείας; ), which arguably included the Great Library of Alexandria, was an institution said to have been founded by Ptolemy I Soter and his son Ptolemy II Ph ...
of Alexandria
Alexandria ( or ; ar, ٱلْإِسْكَنْدَرِيَّةُ ; grc-gre, Αλεξάνδρεια, Alexándria) is the second largest city in Egypt, and the largest city on the Mediterranean coast. Founded in by Alexander the Great, Alexandria ...
. It was there that Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
(c. 300 BC) taught, and wrote the '' Elements'', widely considered the most successful and influential textbook of all time. The ''Elements'' introduced mathematical rigor
Rigour (British English) or rigor (American English; see spelling differences) describes a condition of stiffness or strictness. These constraints may be environmentally imposed, such as "the rigours of famine"; logically imposed, such as m ...
through the axiomatic method
In mathematics and logic, an axiomatic system is any set of axioms from which some or all axioms can be used in conjunction to logically derive theorems. A theory is a consistent, relatively-self-contained body of knowledge which usually conta ...
and is the earliest example of the format still used in mathematics today, that of definition, axiom, theorem, and proof. Although most of the contents of the ''Elements'' were already known, Euclid arranged them into a single, coherent logical framework. The ''Elements'' was known to all educated people in the West up through the middle of the 20th century and its contents are still taught in geometry classes today. In addition to the familiar theorems of Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
, the ''Elements'' was meant as an introductory textbook to all mathematical subjects of the time, such as number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
, algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
and solid geometry
In mathematics, solid geometry or stereometry is the traditional name for the geometry of Three-dimensional space, three-dimensional, Euclidean spaces (i.e., 3D geometry).
Stereometry deals with the measurements of volumes of various solid fig ...
, including proofs that the square root of two is irrational and that there are infinitely many prime numbers. Euclid also wrote extensively on other subjects, such as conic sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special ...
, optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultraviole ...
, spherical geometry
300px, A sphere with a spherical triangle on it.
Spherical geometry is the geometry of the two-dimensional surface of a sphere. In this context the word "sphere" refers only to the 2-dimensional surface and other terms like "ball" or "solid sp ...
, and mechanics, but only half of his writings survive.
Archimedes
Archimedes of Syracuse (;; ) was a Greek mathematician, physicist, engineer, astronomer, and inventor from the ancient city of Syracuse in Sicily. Although few details of his life are known, he is regarded as one of the leading scientists ...
(c. 287–212 BC) of Syracuse, widely considered the greatest mathematician of antiquity, used the method of exhaustion
The method of exhaustion (; ) is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area bet ...
to calculate the area
Area is the quantity that expresses the extent of a region on the plane or on a curved surface. The area of a plane region or ''plane area'' refers to the area of a shape
A shape or figure is a graphics, graphical representation of an obje ...
under the arc of a parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descript ...
with the summation of an infinite series, in a manner not too dissimilar from modern calculus. He also showed one could use the method of exhaustion to calculate the value of π with as much precision as desired, and obtained the most accurate value of π then known, . He also studied the spiral
In mathematics, a spiral is a curve which emanates from a point, moving farther away as it revolves around the point.
Helices
Two major definitions of "spiral" in the American Heritage Dictionary are:volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The de ...
s of surfaces of revolution
A surface of revolution is a surface in Euclidean space created by rotating a curve (the generatrix) around an axis of rotation.
Examples of surfaces of revolution generated by a straight line are cylindrical and conical surfaces depending on ...
(paraboloid, ellipsoid, hyperboloid), and an ingenious method of exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to re ...
for expressing very large numbers. While he is also known for his contributions to physics and several advanced mechanical devices, Archimedes himself placed far greater value on the products of his thought and general mathematical principles. He regarded as his greatest achievement his finding of the surface area and volume of a sphere, which he obtained by proving these are 2/3 the surface area and volume of a cylinder circumscribing the sphere.

Apollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contribution ...
(c. 262–190 BC) made significant advances to the study of conic sections
In mathematics, a conic section, quadratic curve or conic is a curve obtained as the intersection of the surface of a cone with a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special ...
, showing that one can obtain all three varieties of conic section by varying the angle of the plane that cuts a double-napped cone. He also coined the terminology in use today for conic sections, namely parabola
In mathematics, a parabola is a plane curve which is mirror-symmetrical and is approximately U-shaped. It fits several superficially different mathematical descriptions, which can all be proved to define exactly the same curves.
One descript ...
("place beside" or "comparison"), "ellipse" ("deficiency"), and "hyperbola" ("a throw beyond"). His work ''Conics'' is one of the best known and preserved mathematical works from antiquity, and in it he derives many theorems concerning conic sections that would prove invaluable to later mathematicians and astronomers studying planetary motion, such as Isaac Newton. While neither Apollonius nor any other Greek mathematicians made the leap to coordinate geometry, Apollonius' treatment of curves is in some ways similar to the modern treatment, and some of his work seems to anticipate the development of analytical geometry by Descartes some 1800 years later.
Around the same time, Eratosthenes of Cyrene
Eratosthenes of Cyrene (; grc-gre, Ἐρατοσθένης ; – ) was a Greek polymath: a mathematician, geographer, poet, astronomer, and music theorist. He was a man of learning, becoming the chief librarian at the Library of Alexandria ...
(c. 276–194 BC) devised the Sieve of Eratosthenes
In mathematics, the sieve of Eratosthenes is an ancient algorithm for finding all prime numbers up to any given limit.
It does so by iteratively marking as composite (i.e., not prime) the multiples of each prime, starting with the first prime n ...
for finding prime numbers
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
. The 3rd century BC is generally regarded as the "Golden Age" of Greek mathematics, with advances in pure mathematics henceforth in relative decline. Nevertheless, in the centuries that followed significant advances were made in applied mathematics, most notably trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. T ...
, largely to address the needs of astronomers. Hipparchus of Nicaea
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equi ...
(c. 190–120 BC) is considered the founder of trigonometry for compiling the first known trigonometric table, and to him is also due the systematic use of the 360 degree circle. Heron of Alexandria
Hero of Alexandria (; grc-gre, Ἥρων ὁ Ἀλεξανδρεύς, ''Heron ho Alexandreus'', also known as Heron of Alexandria ; 60 AD) was a Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egypt. He ...
(c. 10–70 AD) is credited with Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is,
:A = \sqrt.
It is named after first-century ...
for finding the area of a scalene triangle and with being the first to recognize the possibility of negative numbers possessing square roots. Menelaus of Alexandria
Menelaus of Alexandria (; grc-gre, Μενέλαος ὁ Ἀλεξανδρεύς, ''Menelaos ho Alexandreus''; c. 70 – 140 CE) was a GreekEncyclopædia Britannica "Greek mathematician and astronomer who first conceived and defined a spheric ...
(c. 100 AD) pioneered spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gr ...
through Menelaus' theorem
Menelaus's theorem, named for Menelaus of Alexandria, is a proposition about triangles in plane geometry. Suppose we have a triangle ''ABC'', and a transversal line that crosses ''BC'', ''AC'', and ''AB'' at points ''D'', ''E'', and ''F'' respec ...
. The most complete and influential trigonometric work of antiquity is the ''Almagest
The ''Almagest'' is a 2nd-century Greek-language mathematical and astronomical treatise on the apparent motions of the stars and planetary paths, written by Claudius Ptolemy ( ). One of the most influential scientific texts in history, it canoni ...
'' of Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importanc ...
(c. AD 90–168), a landmark astronomical treatise whose trigonometric tables would be used by astronomers for the next thousand years. Ptolemy is also credited with Ptolemy's theorem
In Euclidean geometry, Ptolemy's theorem is a relation between the four sides and two diagonals of a cyclic quadrilateral (a quadrilateral whose vertices lie on a common circle). The theorem is named after the Greek astronomer and mathematician ...
for deriving trigonometric quantities, and the most accurate value of π outside of China until the medieval period, 3.1416.
 Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics. During this period,
Following a period of stagnation after Ptolemy, the period between 250 and 350 AD is sometimes referred to as the "Silver Age" of Greek mathematics. During this period, Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
made significant advances in algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
, particularly indeterminate analysis, which is also known as "Diophantine analysis". The study of Diophantine equations
In mathematics, a Diophantine equation is an equation, typically a polynomial equation in two or more unknowns with integer coefficients, such that the only solutions of interest are the integer ones. A linear Diophantine equation equates to a c ...
and Diophantine approximations
In number theory, the study of Diophantine approximation deals with the approximation of real numbers by rational numbers. It is named after Diophantus of Alexandria.
The first problem was to know how well a real number can be approximated by r ...
is a significant area of research to this day. His main work was the ''Arithmetica'', a collection of 150 algebraic problems dealing with exact solutions to determinate and indeterminate equation In mathematics, particularly in algebra, an indeterminate equation is an equation for which there is more than one solution. For example, the equation ax + by =c is a simple indeterminate equation, as is x^2=1. Indeterminate equations cannot be solv ...
s. The ''Arithmetica'' had a significant influence on later mathematicians, such as Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
, who arrived at his famous Last Theorem after trying to generalize a problem he had read in the ''Arithmetica'' (that of dividing a square into two squares). Diophantus also made significant advances in notation, the ''Arithmetica'' being the first instance of algebraic symbolism and syncopation.
 Among the last great Greek mathematicians is
Among the last great Greek mathematicians is Pappus of Alexandria
Pappus of Alexandria (; grc-gre, Πάππος ὁ Ἀλεξανδρεύς; AD) was one of the last great Greek mathematicians of antiquity known for his ''Synagoge'' (Συναγωγή) or ''Collection'' (), and for Pappus's hexagon theorem i ...
(4th century AD). He is known for his hexagon theorem and centroid theorem, as well as the Pappus configuration
In geometry, the Pappus configuration is a configuration of nine points and nine lines in the Euclidean plane, with three points per line and three lines through each point.
History and construction
This configuration is named after Pappus of ...
and Pappus graph
In the mathematical field of graph theory, the Pappus graph is a bipartite 3- regular undirected graph with 18 vertices and 27 edges, formed as the Levi graph of the Pappus configuration. It is named after Pappus of Alexandria, an ancient Greek ...
. His ''Collection'' is a major source of knowledge on Greek mathematics as most of it has survived. Pappus is considered the last major innovator in Greek mathematics, with subsequent work consisting mostly of commentaries on earlier work.
The first woman mathematician recorded by history was Hypatia
Hypatia, Koine pronunciation (born 350–370; died 415 AD) was a neoplatonist philosopher, astronomer, and mathematician, who lived in Alexandria, Egypt, then part of the Eastern Roman Empire. She was a prominent thinker in Alexandria wher ...
of Alexandria (AD 350–415). She succeeded her father (Theon of Alexandria
Theon of Alexandria (; grc, Θέων ὁ Ἀλεξανδρεύς; 335 – c. 405) was a Greek scholar and mathematician who lived in Alexandria, Egypt. He edited and arranged Euclid's '' Elements'' and wrote commentaries on works ...
) as Librarian at the Great Library and wrote many works on applied mathematics. Because of a political dispute, the Christian community in Alexandria had her stripped publicly and executed. Her death is sometimes taken as the end of the era of the Alexandrian Greek mathematics, although work did continue in Athens for another century with figures such as Proclus
Proclus Lycius (; 8 February 412 – 17 April 485), called Proclus the Successor ( grc-gre, Πρόκλος ὁ Διάδοχος, ''Próklos ho Diádokhos''), was a Greek Neoplatonist philosopher, one of the last major classical philosophers ...
, Simplicius and Eutocius
Eutocius of Ascalon (; el, Εὐτόκιος ὁ Ἀσκαλωνίτης; 480s – 520s) was a Palestinian-Greek mathematician who wrote commentaries on several Archimedean treatises and on the Apollonian ''Conics''.
Life and work
Little is ...
. Although Proclus and Simplicius were more philosophers than mathematicians, their commentaries on earlier works are valuable sources on Greek mathematics. The closure of the neo-Platonic Academy of Athens by the emperor Justinian
Justinian I (; la, Iustinianus, ; grc-gre, Ἰουστινιανός ; 48214 November 565), also known as Justinian the Great, was the Byzantine emperor from 527 to 565.
His reign is marked by the ambitious but only partly realized ''renovat ...
in 529 AD is traditionally held as marking the end of the era of Greek mathematics, although the Greek tradition continued unbroken in the Byzantine empire
The Byzantine Empire, also referred to as the Eastern Roman Empire or Byzantium, was the continuation of the Roman Empire primarily in its eastern provinces during Late Antiquity and the Middle Ages, when its capital city was Constantinopl ...
with mathematicians such as Anthemius of Tralles
Anthemius of Tralles ( grc-gre, Ἀνθέμιος ὁ Τραλλιανός, Medieval Greek: , ''Anthémios o Trallianós''; – 533 558) was a Greek from Tralles who worked as a geometer and architect in Constantinople, the capi ...
and Isidore of Miletus
Isidore of Miletus ( el, Ἰσίδωρος ὁ Μιλήσιος; Medieval Greek pronunciation: ; la, Isidorus Miletus) was one of the two main Byzantine Greek architects (Anthemius of Tralles was the other) that Emperor Justinian I commissioned ...
, the architects of the Hagia Sophia
Hagia Sophia ( 'Holy Wisdom'; ; ; ), officially the Hagia Sophia Grand Mosque ( tr, Ayasofya-i Kebir Cami-i Şerifi), is a mosque and major cultural and historical site in Istanbul, Turkey. The cathedral was originally built as a Greek Ortho ...
. Nevertheless, Byzantine mathematics consisted mostly of commentaries, with little in the way of innovation, and the centers of mathematical innovation were to be found elsewhere by this time.
Roman
 Although
Although ethnic Greek
The Greeks or Hellenes (; el, Έλληνες, ''Éllines'' ) are an ethnic group and nation indigenous to the Eastern Mediterranean and the Black Sea regions, namely Greece, Cyprus, Albania, Italy, Turkey, Egypt, and, to a lesser extent, oth ...
mathematicians continued under the rule of the late Roman Republic
The Roman Republic ( la, Res publica Romana ) was a form of government of Rome and the era of the classical Roman civilization when it was run through public representation of the Roman people. Beginning with the overthrow of the Roman Kin ...
and subsequent Roman Empire
The Roman Empire ( la, Imperium Romanum ; grc-gre, Βασιλεία τῶν Ῥωμαίων, Basileía tôn Rhōmaíōn) was the post-Republican period of ancient Rome. As a polity, it included large territorial holdings around the Mediterr ...
, there were no noteworthy native Latin mathematicians in comparison. Ancient Romans
In modern historiography, ancient Rome refers to Roman people, Roman civilisation from the founding of the city of Rome in the 8th century BC to the collapse of the Western Roman Empire in the 5th century AD. It encompasses the Roman Kingdom ...
such as Cicero
Marcus Tullius Cicero ( ; ; 3 January 106 BC – 7 December 43 BC) was a Roman statesman, lawyer, scholar, philosopher, and academic skeptic, who tried to uphold optimate principles during the political crises that led to the estab ...
(106–43 BC), an influential Roman statesman who studied mathematics in Greece, believed that Roman surveyor
Surveying or land surveying is the technique, profession, art, and science of determining the terrestrial two-dimensional or three-dimensional positions of points and the distances and angles between them. A land surveying professional is ca ...
s and calculators
An electronic calculator is typically a portable electronic device used to perform calculations, ranging from basic arithmetic to complex mathematics.
The first solid-state electronic calculator was created in the early 1960s. Pocket-size ...
were far more interested in applied mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical s ...
than the theoretical mathematics
Pure mathematics is the study of mathematical concepts independently of any application outside mathematics. These concepts may originate in real-world concerns, and the results obtained may later turn out to be useful for practical applications ...
and geometry that were prized by the Greeks. It is unclear if the Romans first derived their numerical system directly from the Greek precedent or from Etruscan numerals
Etruscan numerals are the words and phrases for numbers of the Etruscan language, and the numerical digits used to write them.
Digits
The Etruscan numerical system included the following digits with known values:Gilles Van Heems (2009)>Nombre, c ...
used by the Etruscan civilization
The Etruscan civilization () was developed by a people of Etruria in ancient Italy with a common language and culture who formed a federation of city-states. After conquering adjacent lands, its territory covered, at its greatest extent, roughl ...
centered in what is now Tuscany
Tuscany ( ; it, Toscana ) is a Regions of Italy, region in central Italy with an area of about and a population of about 3.8 million inhabitants. The regional capital is Florence (''Firenze'').
Tuscany is known for its landscapes, history, art ...
, central Italy
Central Italy ( it, Italia centrale or just ) is one of the five official statistical regions of Italy used by the National Institute of Statistics (ISTAT), a first-level NUTS region, and a European Parliament constituency.
Regions
Central It ...
.
Using calculation, Romans were adept at both instigating and detecting financial fraud
In law, fraud is intentional deception to secure unfair or unlawful gain, or to deprive a victim of a legal right. Fraud can violate civil law (e.g., a fraud victim may sue the fraud perpetrator to avoid the fraud or recover monetary compens ...
, as well as managing taxes for the treasury
A treasury is either
*A government department related to finance and taxation, a finance ministry.
*A place or location where treasure, such as currency or precious items are kept. These can be state or royal property, church treasure or in p ...
. Siculus Flaccus Siculus Flaccus (date uncertain) was an ancient Roman '' gromaticus'' (land surveyor), and writer in Latin on land surveying. His work was included in a collection of gromatic treatises in the 6th century AD.
Siculus Flaccus made the distinction b ...
, one of the Roman ''gromatici
''Gromatici'' (from Latin '' groma'' or ''gruma'', a surveyor's pole) or ''agrimensores'' was the name for land surveyors amongst the ancient Romans. The "gromatic writers" were technical writers who codified their techniques of surveying, most ...
'' (i.e. land surveyor), wrote the ''Categories of Fields'', which aided Roman surveyors in measuring the surface area
The surface area of a solid object is a measure of the total area that the surface of the object occupies. The mathematical definition of surface area in the presence of curved surfaces is considerably more involved than the definition of arc ...
s of allotted lands and territories. Aside from managing trade and taxes, the Romans also regularly applied mathematics to solve problems in engineering
Engineering is the use of scientific method, scientific principles to design and build machines, structures, and other items, including bridges, tunnels, roads, vehicles, and buildings. The discipline of engineering encompasses a broad rang ...
, including the erection of architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and constructing building ...
such as bridges
A bridge is a structure built to Span (engineering), span a physical obstacle (such as a body of water, valley, road, or rail) without blocking the way underneath. It is constructed for the purpose of providing passage over the obstacle, whic ...
, road-building, and preparation for military campaigns. Arts and crafts
A handicraft, sometimes more precisely expressed as artisanal handicraft or handmade, is any of a wide variety of types of work where useful and decorative objects are made completely by one’s hand or by using only simple, non-automated re ...
such as Roman mosaic
A Roman mosaic is a mosaic made during the Roman period, throughout the Roman Republic and later Empire. Mosaics were used in a variety of private and public buildings, on both floors and walls, though they competed with cheaper frescos for the ...
s, inspired by previous Greek designs, created illusionist geometric patterns and rich, detailed scenes that required precise measurements for each tessera
A tessera (plural: tesserae, diminutive ''tessella'') is an individual tile, usually formed in the shape of a square, used in creating a mosaic. It is also known as an abaciscus or abaculus.
Historical tesserae
The oldest known tesserae ...
tile, the opus tessellatum
''Opus tessellatum'' is the Latin name for the normal technique of Greek and Roman mosaic, made from tesserae that are larger than about 4 mm. It is distinguished from the finer ''opus vermiculatum'' which used tiny ''tesserae'', typically cubes ...
pieces on average measuring eight millimeters square and the finer opus vermiculatum
''Opus vermiculatum'' is a method of laying mosaic tesserae to emphasise an outline around a subject. This can be of one or more rows and may also provide background contrast, e.g. as a shadow, sometimes with ''opus tessellatum''. The outline cr ...
pieces having an average surface of four millimeters square.
The creation of the Roman calendar
The Roman calendar was the calendar used by the Roman Kingdom and Roman Republic. The term often includes the Julian calendar established by the reforms of the Roman dictator, dictator Julius Caesar and Roman emperor, emperor Augustus in the ...
also necessitated basic mathematics. The first calendar allegedly dates back to 8th century BC during the Roman Kingdom
The Roman Kingdom (also referred to as the Roman monarchy, or the regal period of ancient Rome) was the earliest period of Roman history when the city and its territory were ruled by kings. According to oral accounts, the Roman Kingdom began wi ...
and included 356 days plus a leap year
A leap year (also known as an intercalary year or bissextile year) is a calendar year that contains an additional day (or, in the case of a lunisolar calendar, a month) added to keep the calendar year synchronized with the astronomical year or s ...
every other year. In contrast, the lunar calendar
A lunar calendar is a calendar based on the monthly cycles of the Moon's phases (synodic months, lunations), in contrast to solar calendars, whose annual cycles are based only directly on the solar year. The most commonly used calendar, the Gre ...
of the Republican era contained 355 days, roughly ten-and-one-fourth days shorter than the solar year
A tropical year or solar year (or tropical period) is the time that the Sun takes to return to the same position in the sky of a celestial body of the Solar System such as the Earth, completing a full cycle of seasons; for example, the time fro ...
, a discrepancy that was solved by adding an extra month into the calendar after the 23rd of February. This calendar was supplanted by the Julian calendar
The Julian calendar, proposed by Roman consul Julius Caesar in 46 BC, was a reform of the Roman calendar. It took effect on , by edict. It was designed with the aid of Greek mathematicians and astronomers such as Sosigenes of Alexandr ...
, a solar calendar
A solar calendar is a calendar whose dates indicate the season or almost equivalently the apparent position of the Sun relative to the stars. The Gregorian calendar, widely accepted as a standard in the world, is an example of a solar calendar.
T ...
organized by Julius Caesar
Gaius Julius Caesar (; ; 12 July 100 BC – 15 March 44 BC), was a Roman general and statesman. A member of the First Triumvirate, Caesar led the Roman armies in the Gallic Wars before defeating his political rival Pompey in a civil war, and ...
(100–44 BC) and devised by Sosigenes of Alexandria
Sosigenes ( grc-gre, Σωσιγένης) was an ancient astronomer. According to Pliny the Elder's '' Natural History'' 18.210–212, Julius Caesar consulted him while he was designing the Julian calendar.
Biography
Little is known about him a ...
to include a leap day
February 29, also known as leap day or leap year day, is a date added to leap years. A leap day is added in various solar calendars (calendars based on the Earth's revolution around the Sun), including the Gregorian calendar standard in mo ...
every four years in a 365-day cycle. This calendar, which contained an error of 11 minutes and 14 seconds, was later corrected by the Gregorian calendar
The Gregorian calendar is the calendar used in most parts of the world. It was introduced in October 1582 by Pope Gregory XIII as a modification of, and replacement for, the Julian calendar. The principal change was to space leap years dif ...
organized by Pope Gregory XIII
Pope Gregory XIII ( la, Gregorius XIII; it, Gregorio XIII; 7 January 1502 – 10 April 1585), born Ugo Boncompagni, was head of the Catholic Church and ruler of the Papal States from 13 May 1572 to his death in April 1585. He is best known for ...
(), virtually the same solar calendar used in modern times as the international standard calendar.
At roughly the same time, the Han Chinese and the Romans both invented the wheeled odometer
An odometer or odograph is an instrument used for measuring the distance traveled by a vehicle, such as a bicycle or car. The device may be electronic, mechanical, or a combination of the two (electromechanical). The noun derives from ancient Gr ...
device for measuring distance
Distance is a numerical or occasionally qualitative measurement of how far apart objects or points are. In physics or everyday usage, distance may refer to a physical length or an estimation based on other criteria (e.g. "two counties over"). ...
s traveled, the Roman model first described by the Roman civil engineer and architect Vitruvius
Vitruvius (; c. 80–70 BC – after c. 15 BC) was a Roman architect and engineer during the 1st century BC, known for his multi-volume work entitled ''De architectura''. He originated the idea that all buildings should have three attribute ...
(c. 80 BC – c. 15 BC). The device was used at least until the reign of emperor Commodus
Commodus (; 31 August 161 – 31 December 192) was a Roman emperor who ruled from 177 to 192. He served jointly with his father Marcus Aurelius from 176 until the latter's death in 180, and thereafter he reigned alone until his assassination. ...
(), but its design seems to have been lost until experiments were made during the 15th century in Western Europe. Perhaps relying on similar gear-work and technology
Technology is the application of knowledge to reach practical goals in a specifiable and reproducible way. The word ''technology'' may also mean the product of such an endeavor. The use of technology is widely prevalent in medicine, science, ...
found in the Antikythera mechanism
The Antikythera mechanism ( ) is an Ancient Greece, Ancient Greek hand-powered orrery, described as the oldest example of an analogue computer used to predict astronomy, astronomical positions and eclipses decades in advance. It could also be ...
, the odometer of Vitruvius featured chariot wheels measuring 4 feet (1.2 m) in diameter turning four-hundred times in one Roman mile
The mile, sometimes the international mile or statute mile to distinguish it from other miles, is a British imperial unit and United States customary unit of distance; both are based on the older English unit of length equal to 5,280 Engli ...
(roughly 4590 ft/1400 m). With each revolution, a pin-and-axle device engaged a 400-tooth cogwheel that turned a second gear responsible for dropping pebbles into a box, each pebble representing one mile traversed.
Chinese
 An analysis of early Chinese mathematics has demonstrated its unique development compared to other parts of the world, leading scholars to assume an entirely independent development. The oldest extant mathematical text from China is the ''
An analysis of early Chinese mathematics has demonstrated its unique development compared to other parts of the world, leading scholars to assume an entirely independent development. The oldest extant mathematical text from China is the ''Zhoubi Suanjing
The ''Zhoubi Suanjing'' () is one of the oldest Chinese mathematical texts. "Zhou" refers to the ancient Zhou dynasty (1046–256 BCE); "Bì" literally means "thigh", but in the book refers to the gnomon of a sundial. The book is dedicated to ...
'', variously dated to between 1200 BC and 100 BC, though a date of about 300 BC during the Warring States Period
The Warring States period () was an era in History of China#Ancient China, ancient Chinese history characterized by warfare, as well as bureaucratic and military reforms and consolidation. It followed the Spring and Autumn period and concluded ...
appears reasonable. However, the Tsinghua Bamboo Slips The Tsinghua Bamboo Strips () are a collection of Chinese texts dating to the Warring States period and written in ink on strips of bamboo, that were acquired in 2008 by Tsinghua University, China. The texts were obtained by illegal excavation, pr ...
, containing the earliest known decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
multiplication table
In mathematics, a multiplication table (sometimes, less formally, a times table) is a mathematical table used to define a multiplication operation for an algebraic system.
The decimal multiplication table was traditionally taught as an essenti ...
(although ancient Babylonians had ones with a base of 60), is dated around 305 BC and is perhaps the oldest surviving mathematical text of China.
Rod numerals
Counting rods () are small bars, typically 3–14 cm long, that were used by mathematicians for calculation in ancient East Asia. They are placed either horizontally or vertically to represent any integer or rational number.
The written fo ...
allowed the representation of numbers as large as desired and allowed calculations to be carried out on the '' suan pan'', or Chinese abacus. The date of the invention of the ''suan pan'' is not certain, but the earliest written mention dates from AD 190, in Xu Yue's ''Supplementary Notes on the Art of Figures''.
The oldest existent work on geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
in China comes from the philosophical Mohist
Mohism or Moism (, ) was an Chinese philosophy#Ancient philosophy, ancient Chinese philosophy of ethics and logic, rational thought, and science developed by the academic scholars who studied under the ancient Chinese philosopher Mozi (c. 470 BC ...
canon c. 330 BC, compiled by the followers of Mozi
Mozi (; ; Latinized as Micius ; – ), original name Mo Di (), was a Chinese philosopher who founded the school of Mohism during the Hundred Schools of Thought period (the early portion of the Warring States period, –221 BCE). The ancie ...
(470–390 BC). The ''Mo Jing'' described various aspects of many fields associated with physical science, and provided a small number of geometrical theorems as well. It also defined the concepts of circumference
In geometry, the circumference (from Latin ''circumferens'', meaning "carrying around") is the perimeter of a circle or ellipse. That is, the circumference would be the arc length of the circle, as if it were opened up and straightened out to ...
, diameter
In geometry, a diameter of a circle is any straight line segment that passes through the center of the circle and whose endpoints lie on the circle. It can also be defined as the longest chord of the circle. Both definitions are also valid for ...
, radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
, and volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). The de ...
.
 In 212 BC, the Emperor
In 212 BC, the Emperor Qin Shi Huang
Qin Shi Huang (, ; 259–210 BC) was the founder of the Qin dynasty and the first emperor of a unified China. Rather than maintain the title of "king" ( ''wáng'') borne by the previous Shang and Zhou rulers, he ruled as the First Emperor ( ...
commanded all books in the Qin Empire
The Qin dynasty ( ; zh, c=秦朝, p=Qín cháo, w=), or Ch'in dynasty in Wade–Giles romanization ( zh, c=, p=, w=Ch'in ch'ao), was the first Dynasties in Chinese history, dynasty of Imperial China. Named for its heartland in Qin (state), ...
other than officially sanctioned ones be burned. This decree was not universally obeyed, but as a consequence of this order little is known about ancient Chinese mathematics before this date. After the book burning
Book burning is the deliberate destruction by fire of books or other written materials, usually carried out in a public context. The burning of books represents an element of censorship and usually proceeds from a cultural, religious, or politi ...
of 212 BC, the Han dynasty
The Han dynasty (, ; ) was an imperial dynasty of China (202 BC – 9 AD, 25–220 AD), established by Liu Bang (Emperor Gao) and ruled by the House of Liu. The dynasty was preceded by the short-lived Qin dynasty (221–207 BC) and a warr ...
(202 BC–220 AD) produced works of mathematics which presumably expanded on works that are now lost. The most important of these is ''The Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' () is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 2nd century CE. This book is one of the earliest sur ...
'', the full title of which appeared by AD 179, but existed in part under other titles beforehand. It consists of 246 word problems involving agriculture, business, employment of geometry to figure height spans and dimension ratios for Chinese pagoda
A pagoda is an Asian tiered tower with multiple eaves common to Nepal, India, China, Japan, Korea, Myanmar, Vietnam, and other parts of Asia. Most pagodas were built to have a religious function, most often Buddhist but sometimes Taoist, ...
towers, engineering, surveying
Surveying or land surveying is the technique, profession, art, and science of determining the terrestrial two-dimensional or three-dimensional positions of points and the distances and angles between them. A land surveying professional is ca ...
, and includes material on right triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right an ...
s. It created mathematical proof for the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
, and a mathematical formula for Gaussian elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of operations performed on the corresponding matrix of coefficients. This method can also be used ...
. The treatise also provides values of π, which Chinese mathematicians originally approximated as 3 until Liu Xin (d. 23 AD) provided a figure of 3.1457 and subsequently Zhang Heng
Zhang Heng (; AD 78–139), formerly romanized as Chang Heng, was a Chinese polymathic scientist and statesman who lived during the Han dynasty. Educated in the capital cities of Luoyang and Chang'an, he achieved success as an astronomer, ma ...
(78–139) approximated pi as 3.1724, as well as 3.162 by taking the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
E ...
of 10. Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu (The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state o ...
commented on the ''Nine Chapters'' in the 3rd century AD and gave a value of π accurate to 5 decimal places (i.e. 3.14159). Though more of a matter of computational stamina than theoretical insight, in the 5th century AD Zu Chongzhi
Zu Chongzhi (; 429–500 AD), courtesy name Wenyuan (), was a Chinese astronomer, mathematician, politician, inventor, and writer during the Liu Song and Southern Qi dynasties. He was most notable for calculating pi as between 3.1415926 and 3 ...
computed the value of π to seven decimal places (between 3.1415926 and 3.1415927), which remained the most accurate value of π for almost the next 1000 years. He also established a method which would later be called Cavalieri's principle
In geometry, Cavalieri's principle, a modern implementation of the method of indivisibles, named after Bonaventura Cavalieri, is as follows:
* 2-dimensional case: Suppose two regions in a plane are included between two parallel lines in that pl ...
to find the volume of a sphere
A sphere () is a Geometry, geometrical object that is a solid geometry, three-dimensional analogue to a two-dimensional circle. A sphere is the Locus (mathematics), set of points that are all at the same distance from a given point in three ...
.
The high-water mark of Chinese mathematics occurred in the 13th century during the latter half of the Song dynasty
The Song dynasty (; ; 960–1279) was an imperial dynasty of China that began in 960 and lasted until 1279. The dynasty was founded by Emperor Taizu of Song following his usurpation of the throne of the Later Zhou. The Song conquered the rest ...
(960–1279), with the development of Chinese algebra. The most important text from that period is the '' Precious Mirror of the Four Elements'' by Zhu Shijie
Zhu Shijie (, 1249–1314), courtesy name Hanqing (), pseudonym Songting (), was a Chinese mathematician and writer. He was a Chinese mathematician during the Yuan Dynasty. Zhu was born close to today's Beijing. Two of his mathematical works ha ...
(1249–1314), dealing with the solution of simultaneous higher order algebraic equations using a method similar to Horner's method
In mathematics and computer science, Horner's method (or Horner's scheme) is an algorithm for polynomial evaluation. Although named after William George Horner, this method is much older, as it has been attributed to Joseph-Louis Lagrange by Hor ...
. The ''Precious Mirror'' also contains a diagram of Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
with coefficients of binomial expansions through the eighth power, though both appear in Chinese works as early as 1100. The Chinese also made use of the complex combinatorial diagram known as the magic square and Magic circle (mathematics), magic circles, described in ancient times and perfected by Yang Hui (AD 1238–1298).
Even after European mathematics began to flourish during the Renaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas ...
, European and Chinese mathematics were separate traditions, with significant Chinese mathematical output in decline from the 13th century onwards. Jesuit missionaries such as Matteo Ricci carried mathematical ideas back and forth between the two cultures from the 16th to 18th centuries, though at this point far more mathematical ideas were entering China than leaving.
Japanese mathematics, Korean numerals, Korean mathematics, and Vietnamese numerals, Vietnamese mathematics are traditionally viewed as stemming from Chinese mathematics and belonging to the Confucian-based East Asian cultural sphere. Korean and Japanese mathematics were heavily influenced by the algebraic works produced during China's Song dynasty, whereas Vietnamese mathematics was heavily indebted to popular works of China's Ming dynasty (1368–1644). For instance, although Vietnamese mathematical treatises were written in either Chinese characters, Chinese or the native Vietnamese Chữ Nôm script, all of them followed the Chinese format of presenting a collection of problems with algorithms for solving them, followed by numerical answers. Mathematics in Vietnam and Korea were mostly associated with the professional court bureaucracy of History of astronomy, mathematicians and astronomers, whereas in Japan it was more prevalent in the realm of private schools.
Indian
 The earliest civilization on the Indian subcontinent is the Indus Valley civilization (mature phase: 2600 to 1900 BC) that flourished in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a squaring the circle, circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the
The earliest civilization on the Indian subcontinent is the Indus Valley civilization (mature phase: 2600 to 1900 BC) that flourished in the Indus river basin. Their cities were laid out with geometric regularity, but no known mathematical documents survive from this civilization.
The oldest extant mathematical records from India are the Sulba Sutras (dated variously between the 8th century BC and the 2nd century AD), appendices to religious texts which give simple rules for constructing altars of various shapes, such as squares, rectangles, parallelograms, and others. As with Egypt, the preoccupation with temple functions points to an origin of mathematics in religious ritual. The Sulba Sutras give methods for constructing a squaring the circle, circle with approximately the same area as a given square, which imply several different approximations of the value of π. In addition, they compute the square root
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
E ...
of 2 to several decimal places, list Pythagorean triples, and give a statement of the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
. All of these results are present in Babylonian mathematics, indicating Mesopotamian influence. It is not known to what extent the Sulba Sutras influenced later Indian mathematicians. As in China, there is a lack of continuity in Indian mathematics; significant advances are separated by long periods of inactivity.
Pāṇini (c. 5th century BC) formulated the rules for Sanskrit grammar. His notation was similar to modern mathematical notation, and used metarules, Transformation (geometry), transformations, and recursion. Pingala (roughly 3rd–1st centuries BC) in his treatise of Prosody (poetry), prosody uses a device corresponding to a binary numeral system. His discussion of the combinatorics of Metre (music), meters corresponds to an elementary version of the binomial theorem. Pingala's work also contains the basic ideas of Fibonacci numbers (called ''mātrāmeru'').
The next significant mathematical documents from India after the ''Sulba Sutras'' are the ''Siddhantas'', astronomical treatises from the 4th and 5th centuries AD (Gupta period) showing strong Hellenistic influence. They are significant in that they contain the first instance of trigonometric relations based on the half-chord, as is the case in modern trigonometry, rather than the full chord, as was the case in Ptolemaic trigonometry. Through a series of translation errors, the words "sine" and "cosine" derive from the Sanskrit "jiya" and "kojiya".
Around 500 AD, Aryabhata wrote the ''Aryabhatiya'', a slim volume, written in verse, intended to supplement the rules of calculation used in astronomy and mathematical mensuration, though with no feeling for logic or deductive methodology. Though about half of the entries are wrong, it is in the ''Aryabhatiya'' that the decimal place-value system first appears. Several centuries later, the Islamic mathematics, Muslim mathematician Abu Rayhan Biruni described the ''Aryabhatiya'' as a "mix of common pebbles and costly crystals".
In the 7th century, Brahmagupta identified the Brahmagupta theorem, Brahmagupta's identity and Brahmagupta's formula, and for the first time, in ''Brahmasphutasiddhanta, Brahma-sphuta-siddhanta'', he lucidly explained the use of 0 (number), zero as both a placeholder and decimal digit, and explained the Hindu–Arabic numeral system
The Hindu–Arabic numeral system or Indo-Arabic numeral system Audun HolmeGeometry: Our Cultural Heritage 2000 (also called the Hindu numeral system or Arabic numeral system) is a positional decimal numeral system, and is the most common syste ...
. It was from a translation of this Indian text on mathematics (c. 770) that Islamic mathematicians were introduced to this numeral system, which they adapted as Arabic numerals. Islamic scholars carried knowledge of this number system to Europe by the 12th century, and it has now displaced all older number systems throughout the world. Various symbol sets are used to represent numbers in the Hindu–Arabic numeral system, all of which evolved from the Brahmi numerals. Each of the roughly dozen major scripts of India has its own numeral glyphs. In the 10th century, Halayudha's commentary on Pingala's work contains a study of the Fibonacci sequence and Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
, and describes the formation of a matrix (mathematics), matrix.
In the 12th century, Bhāskara II lived in southern India and wrote extensively on all then known branches of mathematics. His work contains mathematical objects equivalent or approximately equivalent to infinitesimals, derivatives, Mean value theorem, the mean value theorem and the derivative of the sine function. To what extent he anticipated the invention of calculus is a controversial subject among historians of mathematics.
In the 14th century, Madhava of Sangamagrama, the founder of the Kerala School of Astronomy and Mathematics, Kerala School of Mathematics, found the Leibniz formula for pi, Madhava–Leibniz series and obtained from it a Approximations of π#Middle Ages, transformed series, whose first 21 terms he used to compute the value of π as 3.14159265359. Madhava also found Gregory's series, the Madhava-Gregory series to determine the arctangent, the Madhava-Newton power series to determine sine and cosine and Taylor series, the Taylor approximation for sine and cosine functions. In the 16th century, Jyesthadeva consolidated many of the Kerala School's developments and theorems in the ''Yukti-bhāṣā''.
It has been argued that the advances of the Kerala school, which laid the foundations of the calculus, were transmitted to Europe in the 16th century via Jesuit missionaries and traders who were active around the ancient port of Muziris at the time and, as a result, directly influenced later European developments in analysis and calculus. However, other scholars argue that the Kerala School did not formulate a systematic theory of derivative, differentiation and integral, integration, and that there is not any direct evidence of their results being transmitted outside Kerala.
Islamic empires
 The Caliphate, Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberian Peninsula, Iberia, and in parts of History of India, India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic language, Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persian people, Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian people, Persian mathematician
The Caliphate, Islamic Empire established across Persia, the Middle East, Central Asia, North Africa, Iberian Peninsula, Iberia, and in parts of History of India, India in the 8th century made significant contributions towards mathematics. Although most Islamic texts on mathematics were written in Arabic language, Arabic, most of them were not written by Arabs, since much like the status of Greek in the Hellenistic world, Arabic was used as the written language of non-Arab scholars throughout the Islamic world at the time. Persian people, Persians contributed to the world of Mathematics alongside Arabs.
In the 9th century, the Persian people, Persian mathematician Muḥammad ibn Mūsā al-Khwārizmī
Muhammad ( ar, مُحَمَّد; 570 – 8 June 632 CE) was an Arab religious, social, and political leader and the founder of Islam. According to Islamic doctrine, he was a prophet divinely inspired to preach and confirm the mono ...
wrote an important book on the Hindu–Arabic numerals and one on methods for solving equations. His book ''On the Calculation with Hindu Numerals'', written about 825, along with the work of Al-Kindi, were instrumental in spreading Indian mathematics and Hindu–Arabic numeral system, Indian numerals to the West. The word ''algorithm'' is derived from the Latinization of his name, Algoritmi, and the word ''algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
'' from the title of one of his works, ''The Compendious Book on Calculation by Completion and Balancing, Al-Kitāb al-mukhtaṣar fī hīsāb al-ğabr wa’l-muqābala'' (''The Compendious Book on Calculation by Completion and Balancing''). He gave an exhaustive explanation for the algebraic solution of quadratic equations with positive roots, and he was the first to teach algebra in an Elementary algebra, elementary form and for its own sake. He also discussed the fundamental method of "Reduction (mathematics), reduction" and "balancing", referring to the transposition of subtracted terms to the other side of an equation, that is, the cancellation of like terms on opposite sides of the equation. This is the operation which al-Khwārizmī originally described as ''al-jabr''. "It is not certain just what the terms ''al-jabr'' and ''muqabalah'' mean, but the usual interpretation is similar to that implied in the translation above. The word ''al-jabr'' presumably meant something like "restoration" or "completion" and seems to refer to the transposition of subtracted terms to the other side of an equation; the word ''muqabalah'' is said to refer to "reduction" or "balancing" – that is, the cancellation of like terms on opposite sides of the equation." His algebra was also no longer concerned "with a series of problems to be resolved, but an Expository writing, exposition which starts with primitive terms in which the combinations must give all possible prototypes for equations, which henceforward explicitly constitute the true object of study." He also studied an equation for its own sake and "in a generic manner, insofar as it does not simply emerge in the course of solving a problem, but is specifically called on to define an infinite class of problems."
In Egypt, Abu Kamil extended algebra to the set of irrational numbers
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two inte ...
, accepting square roots and fourth roots as solutions and coefficients to quadratic equations. He also developed techniques used to solve three non-linear simultaneous equations with three unknown variables. One unique feature of his works was trying to find all the possible solutions to some of his problems, including one where he found 2676 solutions. His works formed an important foundation for the development of algebra and influenced later mathematicians, such as al-Karaji and Fibonacci.
Further developments in algebra were made by Al-Karaji in his treatise ''al-Fakhri'', where he extends the methodology to incorporate integer powers and integer roots of unknown quantities. Something close to a Mathematical proof, proof by mathematical induction appears in a book written by Al-Karaji around 1000 AD, who used it to prove the binomial theorem, Pascal's triangle
In mathematics, Pascal's triangle is a triangular array of the binomial coefficients that arises in probability theory, combinatorics, and algebra. In much of the Western world, it is named after the French mathematician Blaise Pascal, although ot ...
, and the sum of integral Cube (algebra), cubes. The historian of mathematics, F. Woepcke, praised Al-Karaji for being "the first who introduced the theory of algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
ic calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
." Also in the 10th century, Abul Wafa translated the works of Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
into Arabic. Ibn al-Haytham was the first mathematician to derive the formula for the sum of the fourth powers, using a method that is readily generalizable for determining the general formula for the sum of any integral powers. He performed an integration in order to find the volume of a paraboloid, and was able to generalize his result for the integrals of polynomials up to the Quartic polynomial, fourth degree. He thus came close to finding a general formula for the integrals of polynomials, but he was not concerned with any polynomials higher than the fourth degree.
In the late 11th century, Omar Khayyam wrote ''Discussions of the Difficulties in Euclid'', a book about what he perceived as flaws in Euclid's Elements, Euclid's ''Elements'', especially the parallel postulate. He was also the first to find the general geometric solution to cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s. He was also very influential in calendar reform.
In the 13th century, Nasir al-Din Tusi (Nasireddin) made advances in spherical trigonometry
Spherical trigonometry is the branch of spherical geometry that deals with the metrical relationships between the sides and angles of spherical triangles, traditionally expressed using trigonometric functions. On the sphere, geodesics are gr ...
. He also wrote influential work on Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
's parallel postulate. In the 15th century, Ghiyath al-Kashi computed the value of π to the 16th decimal place. Kashi also had an algorithm for calculating ''n''th roots, which was a special case of the methods given many centuries later by Paolo Ruffini (mathematician), Ruffini and William George Horner, Horner.
Other achievements of Muslim mathematicians during this period include the addition of the decimal point notation to the Arabic numerals, the discovery of all the modern trigonometric functions besides the sine, al-Kindi's introduction of cryptanalysis and frequency analysis, the development of analytic geometry by Ibn al-Haytham, the beginning of algebraic geometry by Omar Khayyam and the development of an Mathematical notation, algebraic notation by Abū al-Hasan ibn Alī al-Qalasādī, al-Qalasādī.
During the time of the Ottoman Empire and Safavid Empire from the 15th century, the development of Islamic mathematics became stagnant.
Maya
 In the Pre-Columbian Americas, the
In the Pre-Columbian Americas, the Maya civilization
The Maya civilization () of the Mesoamerican people is known by its ancient temples and glyphs. Its Maya script is the most sophisticated and highly developed writing system in the pre-Columbian Americas. It is also noted for its art, archit ...
that flourished in Mexico
Mexico (Spanish: México), officially the United Mexican States, is a country in the southern portion of North America. It is bordered to the north by the United States; to the south and west by the Pacific Ocean; to the southeast by Guatema ...
and Central America
Central America ( es, América Central or ) is a subregion of the Americas. Its boundaries are defined as bordering the United States to the north, Colombia to the south, the Caribbean Sea to the east, and the Pacific Ocean to the west. ...
during the 1st millennium AD developed a unique tradition of mathematics that, due to its geographic isolation, was entirely independent of existing European, Egyptian, and Asian mathematics. Maya numerals
The Mayan numeral system was the system to represent numbers and calendar dates in the Maya civilization. It was a vigesimal (base-20) positional numeral system. The numerals are made up of three symbols; zero (a shell), one (a dot) and fiv ...
used a Radix, base of twenty, the vigesimal system, instead of a base of ten that forms the basis of the decimal
The decimal numeral system (also called the base-ten positional numeral system and denary or decanary) is the standard system for denoting integer and non-integer numbers. It is the extension to non-integer numbers of the Hindu–Arabic numeral ...
system used by most modern cultures. The Maya used mathematics to create the Maya calendar as well as to predict astronomical phenomena in their native Maya astronomy. While the concept of zero
0 (zero) is a number representing an empty quantity. In place-value notation
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or ...
had to be inferred in the mathematics of many contemporary cultures, the Maya developed a standard symbol for it.Inca
 The prevailing numeral system was the Decimal, base-ten.
In precolumbian americas the Inca empire had made various accomplishment in mathematical field.The Incas used their own numeral system which has the base ten.
It is also confirmed that the Incas use of the decimal system by the interpretation of the quipus, which are organized in such a way that the knots — according to their location — can represent: units, tens, hundreds, etc.
However, the main confirmation of the use of this system is expressed in the denomination of the numbers in Quechuan languages, Quechua, in which the numbers are developed in decimal form. This can be appreciated in the following table:
The prevailing numeral system was the Decimal, base-ten.
In precolumbian americas the Inca empire had made various accomplishment in mathematical field.The Incas used their own numeral system which has the base ten.
It is also confirmed that the Incas use of the decimal system by the interpretation of the quipus, which are organized in such a way that the knots — according to their location — can represent: units, tens, hundreds, etc.
However, the main confirmation of the use of this system is expressed in the denomination of the numbers in Quechuan languages, Quechua, in which the numbers are developed in decimal form. This can be appreciated in the following table:
Japan
 Most of the mathematics in Japan had either imported from China although many of the mathematical accomplishment was also made by Japanese mathematicans.
One prominent mathematician during Edo period was Seki Takakazu. He created a new algebraic notation system and, motivated by astronomical computations, did work on infinitesimal calculus and Diophantine equations.
He had a significant impact on
Most of the mathematics in Japan had either imported from China although many of the mathematical accomplishment was also made by Japanese mathematicans.
One prominent mathematician during Edo period was Seki Takakazu. He created a new algebraic notation system and, motivated by astronomical computations, did work on infinitesimal calculus and Diophantine equations.
He had a significant impact on calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
. He discovered the Newton or Newton-Raphson method for solving equations (independent from Newton) and also had a version of the Newton interpolation formula.
In 1674, Seki published Hatsubi Sanpō (発微算法), giving solutions to all 15 problems. The method he used is called ''bōsho-hō''. He introduced the use of kanji to represent unknowns and variables in equations.
He also developed Bernoulli numbers independently from Jacob Bernoulli. They are also called as seki numbers. He studied equations treating both positive and negative roots.
His manuscript and other treatises in 1683 show that the Japanese theory of determinate was fully applied to elimination method of arbitrary constant.It is assumed that he had invented the determinants. Seki pushed ahead with elimination theory, based on resultants, in the Kaifukudai no Hō (解伏題之法). To express the resultant, he developed the notion of the determinant.
Mathematicans like Takebe Katahiro played and important role in developing Enri (" circle principle"), a crude analog to the Western calculus. Mathematical Society of Japan/ref> He obtained power series expansion of in 1722, 15 years earlier than Euler. He used Richardson extrapolation in 1695, about 200 years earlier than Richardson. He also computed 41 digits of π, based on polygon approximation and Richardson extrapolation. Ajima Naonobu was credited for introducing
calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
into Japanese mathematics.Ajima also posed the question of inscribing three mutually tangent circles in a triangle; circles are now known as Malfatti circles after the later work of Gian Francesco Malfatti, but two triangle centers derived from them, the Ajima–Malfatti points, are named after Ajima.
Medieval European
ππMedieval European interest in mathematiRichardson.Hey concerns quite different froπe icians. One driving element was the belief that mathematics .vided the key to understanding the created order of nature, frequently justified byPlato
Plato ( ; grc-gre, Πλάτων ; 428/427 or 424/423 – 348/347 BC) was a Greek philosopher born in Athens during the Classical period in Ancient Greece. He founded the Platonist school of thought and the Academy, the first institution ...
's ''Timaeus (dialogue), Timaeus'' and the biblical passage (in the ''Book of Wisdom'') that God had ''ordered all things in measure, and number, and weight''.
Boethius provided a place for mathematics in the curriculum in the 6th century when he coined the term ''quadrivium'' to describe the study of arithmetic, geometry, astronomy, and music. He wrote ''De institutione arithmetica'', a free translation from the Greek of Nicomachus
Nicomachus of Gerasa ( grc-gre, Νικόμαχος; c. 60 – c. 120 AD) was an important ancient mathematician and music theorist, best known for his works ''Introduction to Arithmetic'' and ''Manual of Harmonics'' in Greek. He was born in ...
's ''Introduction to Arithmetic''; ''De institutione musica'', also derived from Greek sources; and a series of excerpts from Euclid
Euclid (; grc-gre, Wikt:Εὐκλείδης, Εὐκλείδης; BC) was an ancient Greek mathematician active as a geometer and logician. Considered the "father of geometry", he is chiefly known for the ''Euclid's Elements, Elements'' trea ...
's '' Elements''. His works were theoretical, rather than practical, and were the basis of mathematical study until the recovery of Greek and Arabic mathematical works.
In the 12th century, European scholars traveled to Spain and Sicily Latin translations of the 12th century, seeking scientific Arabic texts, including al-Khwārizmī's ''The Compendious Book on Calculation by Completion and Balancing'', translated into Latin by Robert of Chester, and the complete text of Euclid's Elements, Euclid's ''Elements'', translated in various versions by Adelard of Bath, Herman of Carinthia, and Gerard of Cremona. These and other new sources sparked a renewal of mathematics.
Leonardo of Pisa, now known as Fibonacci, serendipitously learned about the Hindu–Arabic numerals on a trip to what is now Béjaïa, Algeria with his merchant father. (Europe was still using Roman numerals.) There, he observed a system of arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th ...
(specifically algorism) which due to the positional notation of Hindu–Arabic numerals was much more efficient and greatly facilitated commerce. Leonardo wrote ''Liber Abaci'' in 1202 (updated in 1254) introducing the technique to Europe and beginning a long period of popularizing it. The book also brought to Europe what is now known as the Fibonacci sequence (known to Indian mathematicians for hundreds of years before that) which was used as an unremarkable example within the text.
The 14th century saw the development of new mathematical concepts to investigate a wide range of problems. One important contribution was development of mathematics of local motion.
Thomas Bradwardine proposed that speed (V) increases in arithmetic proportion as the ratio of force (F) to resistance (R) increases in geometric proportion. Bradwardine expressed this by a series of specific examples, but although the logarithm had not yet been conceived, we can express his conclusion anachronistically by writing:
V = log (F/R). Bradwardine's analysis is an example of transferring a mathematical technique used by al-Kindi and Arnald of Villanova to quantify the nature of compound medicines to a different physical problem.
 One of the 14th-century Oxford Calculators, William Heytesbury, lacking differential calculus and the concept of Limit of a function, limits, proposed to measure instantaneous speed "by the path that would be described by [a body] if... it were moved uniformly at the same degree of speed with which it is moved in that given instant".
Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by
One of the 14th-century Oxford Calculators, William Heytesbury, lacking differential calculus and the concept of Limit of a function, limits, proposed to measure instantaneous speed "by the path that would be described by [a body] if... it were moved uniformly at the same degree of speed with which it is moved in that given instant".
Heytesbury and others mathematically determined the distance covered by a body undergoing uniformly accelerated motion (today solved by integration
Integration may refer to:
Biology
*Multisensory integration
*Path integration
* Pre-integration complex, viral genetic material used to insert a viral genome into a host genome
*DNA integration, by means of site-specific recombinase technology, ...
), stating that "a moving body uniformly acquiring or losing that increment [of speed] will traverse in some given time a [distance] completely equal to that which it would traverse if it were moving continuously through the same time with the mean degree [of speed]".
Nicole Oresme at the University of Paris and the Italian Giovanni di Casali independently provided graphical demonstrations of this relationship, asserting that the area under the line depicting the constant acceleration, represented the total distance traveled. In a later mathematical commentary on Euclid's ''Elements'', Oresme made a more detailed general analysis in which he demonstrated that a body will acquire in each successive increment of time an increment of any quality that increases as the odd numbers. Since Euclid had demonstrated the sum of the odd numbers are the square numbers, the total quality acquired by the body increases as the square of the time.Pacific
The residents of the island of Mangareva in French Polynesia were using a hybrid binary-decimal system before 1450. They used it with base 2 rather than base 10 which most of the culture had adopted.Renaissance
During theRenaissance
The Renaissance ( , ) , from , with the same meanings. is a period in European history marking the transition from the Middle Ages to modernity and covering the 15th and 16th centuries, characterized by an effort to revive and surpass ideas ...
, the development of mathematics and of accounting were intertwined. While there is no direct relationship between algebra and accounting, the teaching of the subjects and the books published often intended for the children of merchants who were sent to reckoning schools (in Flanders and Germany) or abacus schools (known as ''abbaco'' in Italy), where they learned the skills useful for trade and commerce. There is probably no need for algebra in performing bookkeeping
Bookkeeping is the recording of financial transactions, and is part of the process of accounting in business and other organizations. It involves preparing source documents for all transactions, operations, and other events of a business. Tr ...
operations, but for complex bartering operations or the calculation of compound interest, a basic knowledge of arithmetic was mandatory and knowledge of algebra was very useful.
Piero della Francesca (c. 1415–1492) wrote books on solid geometry
In mathematics, solid geometry or stereometry is the traditional name for the geometry of Three-dimensional space, three-dimensional, Euclidean spaces (i.e., 3D geometry).
Stereometry deals with the measurements of volumes of various solid fig ...
and Perspective (graphical), linear perspective, including ''De Prospectiva Pingendi (On Perspective for Painting)'', ''Trattato d’Abaco (Abacus Treatise)'', and ''De quinque corporibus regularibus (On the Five Regular Solids)''.
Luca Pacioli's ''Summa de arithmetica, Summa de Arithmetica, Geometria, Proportioni et Proportionalità'' (Italian: "Review of Arithmetic, Geometry, Ratio and Proportionality (mathematics), Proportion") was first printed and published in Venice in 1494. It included a 27-page treatise on bookkeeping
Bookkeeping is the recording of financial transactions, and is part of the process of accounting in business and other organizations. It involves preparing source documents for all transactions, operations, and other events of a business. Tr ...
, ''"Particularis de Computis et Scripturis"'' (Italian: "Details of Calculation and Recording"). It was written primarily for, and sold mainly to, merchants who used the book as a reference text, as a source of pleasure from the mathematical puzzles it contained, and to aid the education of their sons. In ''Summa Arithmetica'', Pacioli introduced symbols for plus and minus for the first time in a printed book, symbols that became standard notation in Italian Renaissance mathematics. ''Summa Arithmetica'' was also the first known book printed in Italy to contain algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary a ...
. Pacioli obtained many of his ideas from Piero Della Francesca whom he plagiarized.
In Italy, during the first half of the 16th century, Scipione del Ferro and Niccolò Fontana Tartaglia discovered solutions for cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
s. Gerolamo Cardano published them in his 1545 book ''Ars Magna (Gerolamo Cardano), Ars Magna'', together with a solution for the quartic equations, discovered by his student Lodovico Ferrari. In 1572 Rafael Bombelli published his ''L'Algebra'' in which he showed how to deal with the imaginary number, imaginary quantities that could appear in Cardano's formula for solving cubic equations.
Simon Stevin's book ''De Thiende'' ('the art of tenths'), first published in Dutch in 1585, contained the first systematic treatment of decimal notation, which influenced all later work on the real number system.
Driven by the demands of navigation and the growing need for accurate maps of large areas, trigonometry
Trigonometry () is a branch of mathematics that studies relationships between side lengths and angles of triangles. The field emerged in the Hellenistic world during the 3rd century BC from applications of geometry to astronomical studies. T ...
grew to be a major branch of mathematics. Bartholomaeus Pitiscus was the first to use the word, publishing his ''Trigonometria'' in 1595. Regiomontanus's table of sines and cosines was published in 1533.
During the Renaissance the desire of artists to represent the natural world realistically, together with the rediscovered philosophy of the Greeks, led artists to study mathematics. They were also the engineers and architects of that time, and so had need of mathematics in any case. The art of painting in perspective, and the developments in geometry that involved, were studied intensely.
Mathematics during the Scientific Revolution
17th century
 The 17th century saw an unprecedented increase of mathematical and scientific ideas across Europe. Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. By his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion.
The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.
Building on earlier work by many predecessors,
The 17th century saw an unprecedented increase of mathematical and scientific ideas across Europe. Galileo observed the moons of Jupiter in orbit about that planet, using a telescope based on a toy imported from Holland. Tycho Brahe had gathered an enormous quantity of mathematical data describing the positions of the planets in the sky. By his position as Brahe's assistant, Johannes Kepler was first exposed to and seriously interacted with the topic of planetary motion. Kepler's calculations were made simpler by the contemporaneous invention of logarithms by John Napier and Jost Bürgi. Kepler succeeded in formulating mathematical laws of planetary motion.
The analytic geometry developed by René Descartes (1596–1650) allowed those orbits to be plotted on a graph, in Cartesian coordinates.
Building on earlier work by many predecessors, Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a "natural philosopher"), widely recognised as one of the grea ...
discovered the laws of physics explaining Kepler's Laws, and brought together the concepts now known as calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
. Independently, Gottfried Wilhelm Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathema ...
, developed calculus and much of the calculus notation still in use today. Science and mathematics had become an international endeavor, which would soon spread over the entire world.
In addition to the application of mathematics to the studies of the heavens, applied mathematics
Applied mathematics is the application of mathematical methods by different fields such as physics, engineering, medicine, biology, finance, business, computer science, and industry. Thus, applied mathematics is a combination of mathematical s ...
began to expand into new areas, with the correspondence of Pierre de Fermat
Pierre de Fermat (; between 31 October and 6 December 1607 – 12 January 1665) was a French mathematician who is given credit for early developments that led to infinitesimal calculus, including his technique of adequality. In particular, he ...
and Blaise Pascal. Pascal and Fermat set the groundwork for the investigations of probability theory and the corresponding rules of combinatorics in their discussions over a game of gambling. Pascal, with his Pascal's Wager, wager, attempted to use the newly developing probability theory to argue for a life devoted to religion, on the grounds that even if the probability of success was small, the rewards were infinite. In some sense, this foreshadowed the development of utility theory in the 18th–19th century.
18th century
 The most influential mathematician of the 18th century was arguably Leonhard Euler (1707–1783). His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol Imaginary unit, ''i'', and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
The most influential mathematician of the 18th century was arguably Leonhard Euler (1707–1783). His contributions range from founding the study of graph theory with the Seven Bridges of Königsberg problem to standardizing many modern mathematical terms and notations. For example, he named the square root of minus 1 with the symbol Imaginary unit, ''i'', and he popularized the use of the Greek letter to stand for the ratio of a circle's circumference to its diameter. He made numerous contributions to the study of topology, graph theory, calculus, combinatorics, and complex analysis, as evidenced by the multitude of theorems and notations named for him.
Other important European mathematicians of the 18th century included Joseph Louis Lagrange, who did pioneering work in number theory, algebra, differential calculus, and the calculus of variations, and Laplace who, in the age of Napoleon, did important work on the foundations of celestial mechanics and on statistics.
Modern
19th century
Throughout the 19th century mathematics became increasingly abstract. Carl Friedrich Gauss (1777–1855) epitomizes this trend. He did revolutionary work on function (mathematics), functions of complex variables, ingeometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, and on the convergence of series (mathematics), series, leaving aside his many contributions to science. He also gave the first satisfactory proofs of the fundamental theorem of algebra and of the quadratic reciprocity law.
This century saw the development of the two forms of non-Euclidean geometry, where the parallel postulate of Euclidean geometry
Euclidean geometry is a mathematical system attributed to ancient Greek mathematics, Greek mathematician Euclid, which he described in his textbook on geometry: the ''Euclid's Elements, Elements''. Euclid's approach consists in assuming a small ...
no longer holds.
The Russian mathematician Nikolai Ivanovich Lobachevsky and his rival, the Hungarian mathematician János Bolyai, independently defined and studied hyperbolic geometry, where uniqueness of parallels no longer holds. In this geometry the sum of angles in a triangle add up to less than 180°. Elliptic geometry was developed later in the 19th century by the German mathematician Bernhard Riemann; here no parallel can be found and the angles in a triangle add up to more than 180°. Riemann also developed Riemannian geometry, which unifies and vastly generalizes the three types of geometry, and he defined the concept of a manifold, which generalizes the ideas of curves and Surface (topology), surfaces.
The 19th century saw the beginning of a great deal of abstract algebra. Hermann Grassmann in Germany gave a first version of vector spaces, William Rowan Hamilton in Ireland developed noncommutative algebra. The British mathematician George Boole devised an algebra that soon evolved into what is now called Boolean algebra, in which the only numbers were 0 and 1. Boolean algebra is the starting point of mathematical logic and has important applications in electrical engineering and computer science.
Augustin-Louis Cauchy, Bernhard Riemann, and Karl Weierstrass reformulated the calculus in a more rigorous fashion.
Also, for the first time, the limits of mathematics were explored. Niels Henrik Abel, a Norwegian, and Évariste Galois, a Frenchman, proved that there is no general algebraic method for solving polynomial equations of degree greater than four (Abel–Ruffini theorem). Other 19th-century mathematicians used this in their proofs that straight edge and compass alone are not sufficient to trisect an arbitrary angle, to construct the side of a cube twice the volume of a given cube, nor to construct a square equal in area to a given circle. Mathematicians had vainly attempted to solve all of these problems since the time of the ancient Greeks. On the other hand, the limitation of three dimensions in geometry was surpassed in the 19th century through considerations of parameter space and hypercomplex numbers.
Abel and Galois's investigations into the solutions of various polynomial equations laid the groundwork for further developments of group theory, and the associated fields of abstract algebra. In the 20th century physicists and other scientists have seen group theory as the ideal way to study symmetry.
In the later 19th century, Georg Cantor established the first foundations of set theory, which enabled the rigorous treatment of the notion of infinity and has become the common language of nearly all mathematics. Cantor's set theory, and the rise of mathematical logic in the hands of Peano, L.E.J. Brouwer, David Hilbert, Bertrand Russell, and A.N. Whitehead, initiated a long running debate on the foundations of mathematics.
The 19th century saw the founding of a number of national mathematical societies: the London Mathematical Society in 1865, the Société Mathématique de France in 1872, the Circolo Matematico di Palermo in 1884, the Edinburgh Mathematical Society in 1883, and the American Mathematical Society in 1888. The first international, special-interest society, the Quaternion Society, was formed in 1899, in the context of a hyperbolic quaternion#Historical review, vector controversy.
In 1897, Kurt Hensel introduced p-adic numbers.
20th century
The 20th century saw mathematics become a major profession. Every year, thousands of new Ph.D.s in mathematics were awarded, and jobs were available in both teaching and industry. An effort to catalogue the areas and applications of mathematics was undertaken in Klein's encyclopedia. In a 1900 speech to the International Congress of Mathematicians, David Hilbert set out a list of Hilbert's problems, 23 unsolved problems in mathematics. These problems, spanning many areas of mathematics, formed a central focus for much of 20th-century mathematics. Today, 10 have been solved, 7 are partially solved, and 2 are still open. The remaining 4 are too loosely formulated to be stated as solved or not. Notable historical conjectures were finally proven. In 1976, Wolfgang Haken and Kenneth Appel proved the four color theorem, controversial at the time for the use of a computer to do so. Andrew Wiles, building on the work of others, proved Fermat's Last Theorem in 1995. Paul Cohen (mathematician), Paul Cohen and Kurt Gödel proved that the continuum hypothesis is logical independence, independent of (could neither be proved nor disproved from) the ZFC, standard axioms of set theory. In 1998 Thomas Callister Hales proved the Kepler conjecture. Mathematical collaborations of unprecedented size and scope took place. An example is the classification of finite simple groups (also called the "enormous theorem"), whose proof between 1955 and 2004 required 500-odd journal articles by about 100 authors, and filling tens of thousands of pages. A group of French mathematicians, including Jean Dieudonné and André Weil, publishing under the pseudonym "Nicolas Bourbaki", attempted to exposit all of known mathematics as a coherent rigorous whole. The resulting several dozen volumes has had a controversial influence on mathematical education.calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
and continuous functions, but the rise of computing and communication networks led to an increasing importance of discrete mathematics, discrete concepts and the expansion of combinatorics including graph theory. The speed and data processing abilities of computers also enabled the handling of mathematical problems that were too time-consuming to deal with by pencil and paper calculations, leading to areas such as numerical analysis and symbolic computation. Some of the most important methods and algorithms of the 20th century are: the simplex algorithm, the fast Fourier transform, error-correcting codes, the Kalman filter from control theory and the RSA algorithm of public-key cryptography.
At the same time, deep insights were made about the limitations to mathematics. In 1929 and 1930, it was proved the truth or falsity of all statements formulated about the natural numbers plus either addition or multiplication (but not both), was Decidability (logic), decidable, i.e. could be determined by some algorithm. In 1931, Kurt Gödel found that this was not the case for the natural numbers plus both addition and multiplication; this system, known as Peano arithmetic, was in fact incompleteness theorem, incompletable. (Peano arithmetic is adequate for a good deal of number theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777� ...
, including the notion of prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
.) A consequence of Gödel's two incompleteness theorems is that in any mathematical system that includes Peano arithmetic (including all of mathematical analysis, analysis and geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
), truth necessarily outruns proof, i.e. there are true statements that Incompleteness theorem, cannot be proved within the system. Hence mathematics cannot be reduced to mathematical logic, and David Hilbert's dream of making all of mathematics complete and consistent needed to be reformulated.
One of the more colorful figures in 20th-century mathematics was Srinivasa Aiyangar Ramanujan (1887–1920), an Indian autodidact who conjectured or proved over 3000 theorems, including properties of highly composite numbers, the partition function (number theory), partition function and its asymptotics, and Ramanujan theta function, mock theta functions. He also made major investigations in the areas of gamma functions, modular forms, divergent series, General hypergeometric function, hypergeometric series and prime number
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
theory.
Paul Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. Mathematicians have a game equivalent to the Kevin Bacon Game, which leads to the Erdős number of a mathematician. This describes the "collaborative distance" between a person and Erdős, as measured by joint authorship of mathematical papers.
Emmy Noether has been described by many as the most important woman in the history of mathematics. She studied the theories of ring (mathematics), rings, field (mathematics), fields, and algebra over a field, algebras.
As in most areas of study, the explosion of knowledge in the scientific age has led to specialization: by the end of the century there were hundreds of specialized areas in mathematics and the Mathematics Subject Classification was dozens of pages long. More and more mathematical journals were published and, by the end of the century, the development of the World Wide Web led to online publishing.
21st century
In 2000, the Clay Mathematics Institute announced the seven Millennium Prize Problems, and in 2003 the Poincaré conjecture was solved by Grigori Perelman (who declined to accept an award, as he was critical of the mathematics establishment). Most mathematical journals now have online versions as well as print versions, and many online-only journals are launched. There is an increasing drive toward Open access (publishing), open access publishing, first popularized by arXiv.Future
There are many observable trends in mathematics, the most notable being that the subject is growing ever larger, computers are ever more important and powerful, the application of mathematics to bioinformatics is rapidly expanding, and the volume of data being produced by science and industry, facilitated by computers, is expanding exponentially.See also
* Archives of American Mathematics * History of algebra * History of arithmetic * History of calculus * History of combinatorics * History of the function concept * History of geometry * History of logic * History of mathematicians * History of mathematical notation * History of measurement * History of numbers ** History of ancient numeral systems ** Prehistoric counting * History of number theory * History of statistics * History of trigonometry * History of writing numbers * Kenneth O. May Prize * List of important publications in mathematics * Lists of mathematicians * List of mathematics history topics * Timeline of mathematicsNotes
References
* * * * * * * * * * * * * *Further reading
General
* * * David M. Burton, Burton, David M. ''The History of Mathematics: An Introduction''. McGraw Hill: 1997. * * Morris Kline, Kline, Morris. ''Mathematical Thought from Ancient to Modern Times''. * Dirk Jan Struik, Struik, D.J. (1987). ''A Concise History of Mathematics'', fourth revised edition. Dover Publications, New York.Books on a specific period
* * * Bartel Leendert van der Waerden, van der Waerden, B.L., ''Geometry and Algebra in Ancient Civilizations'', Springer, 1983, .Books on a specific topic
* * * *External links
Documentaries
* BBC (2008). ''The Story of Maths''.Renaissance Mathematics
BBC Radio 4 discussion with Robert Kaplan, Jim Bennett & Jackie Stedall (''In Our Time'', Jun 2, 2005)
Educational material
MacTutor History of Mathematics archive
(John J. O'Connor and Edmund F. Robertson; University of St Andrews, Scotland). An award-winning website containing detailed biographies on many historical and contemporary mathematicians, as well as information on notable curves and various topics in the history of mathematics.
History of Mathematics Home Page
(David E. Joyce; Clark University). Articles on various topics in the history of mathematics with an extensive bibliography.
The History of Mathematics
(David R. Wilkins; Trinity College, Dublin). Collections of material on the mathematics between the 17th and 19th century.
(Jeff Miller). Contains information on the earliest known uses of terms used in mathematics.
(Jeff Miller). Contains information on the history of mathematical notations.
(John Aldrich, University of Southampton) Discusses the origins of the modern mathematical word stock.
(Larry Riddle; Agnes Scott College).
Mathematicians of the African Diaspora
(Scott W. Williams; University at Buffalo).
Notes for MAA minicourse: teaching a course in the history of mathematics. (2009)
(V. Frederick Rickey & Victor J. Katz).
Ancient Rome: The Odometer Of Vitruv
Pictorial (moving) re-construction of Vitusius' Roman ododmeter.
Bibliographies
A Bibliography of Collected Works and Correspondence of Mathematicians
(Steven W. Rockey; Cornell University Library).
Organizations
International Commission for the History of Mathematics
Journals
* ''Historia Mathematica''Convergence
the Mathematical Association of America's online ''Math History'' Magazine
History of Mathematics
Math Archives (University of Tennessee, Knoxville)
History/Biography
The Math Forum (Drexel University)
(Courtright Memorial Library).
(David Calvis; Baldwin-Wallace College) *
Historia de las Matemáticas
(Universidad de La La guna)
(Universidade de Coimbra)
Using History in Math Class
(Bruno Kevius)
(Roberta Tucci) {{History of science History of mathematics, History of science by discipline, Mathematics