Generalized conic on:
[Wikipedia]
[Google]
[Amazon]
In
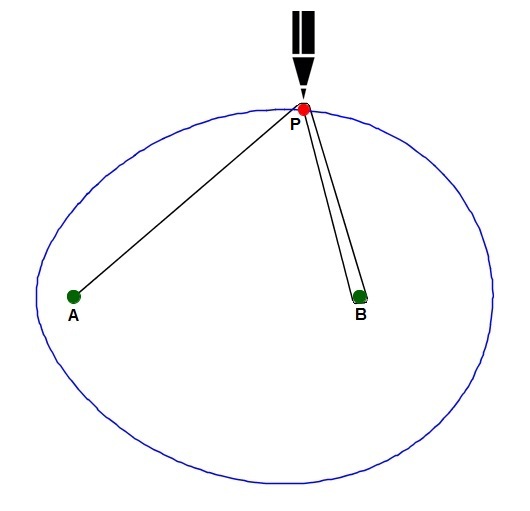


 Given a conic, by choosing a
Given a conic, by choosing a

 If one retains the minimality requirement, then the set of points ''P'' satisfying this requirement are considered to be the primary pseudoconic, and the remainder of the curve is the secondary branch of the pseudoconic. Similar examples of generalized parabolas can be found in Joseph ''et al.''.
If one retains the minimality requirement, then the set of points ''P'' satisfying this requirement are considered to be the primary pseudoconic, and the remainder of the curve is the secondary branch of the pseudoconic. Similar examples of generalized parabolas can be found in Joseph ''et al.''.
mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many ar ...
, a generalized conic is a geometrical object defined by a property which is a generalization
A generalization is a form of abstraction whereby common properties of specific instances are formulated as general concepts or claims. Generalizations posit the existence of a domain or set of elements, as well as one or more common characteri ...
of some defining property of the classical conic
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, thou ...
. For example, in elementary geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
, an ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
can be defined as the locus of a point which moves in a plane such that the sum of its distances from two fixed points – the foci
Focus (: foci or focuses) may refer to:
Arts
* Focus or Focus Festival, former name of the Adelaide Fringe arts festival in East Australia Film
* ''Focus'' (2001 film), a 2001 film based on the Arthur Miller novel
* ''Focus'' (2015 film), a 201 ...
– in the plane is a constant. The curve obtained when the set of two fixed points is replaced by an arbitrary, but fixed, finite set of points in the plane is called an ''n''–ellipse and can be thought of as a generalized ellipse. Since an ellipse is the equidistant set of two circles, where one circle is inside the other, the equidistant set of two arbitrary sets of points in a plane can be viewed as a generalized conic. In rectangular Cartesian coordinates
In geometry, a Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of real numbers called ''coordinates'', which are the signed distances to the point from two fixed perpendicular o ...
, the equation ''y'' = ''x''2 represents a parabola
In mathematics, a parabola is a plane curve which is Reflection symmetry, mirror-symmetrical and is approximately U-shaped. It fits several superficially different Mathematics, mathematical descriptions, which can all be proved to define exactl ...
. The generalized equation ''y'' = ''x'' ''r'', for ''r'' ≠ 0 and ''r'' ≠ 1, can be treated as defining a generalized parabola. The idea of generalized conic has found applications in approximation theory
In mathematics, approximation theory is concerned with how function (mathematics), functions can best be approximation, approximated with simpler functions, and with quantitative property, quantitatively characterization (mathematics), characteri ...
and optimization theory
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criteria, from some set of available alternatives. It is generally divided into two subfiel ...
.
Among the several possible ways in which the concept of a conic can be generalized, the most widely used approach is to define it as a generalization of the ellipse
In mathematics, an ellipse is a plane curve surrounding two focus (geometry), focal points, such that for all points on the curve, the sum of the two distances to the focal points is a constant. It generalizes a circle, which is the special ty ...
. The starting point for this approach is to look upon an ellipse as a curve satisfying the 'two-focus property': an ellipse is a curve that is the locus of points the sum of whose distances from two given points is constant. The two points are the foci of the ellipse. The curve obtained by replacing the set of two fixed points by an arbitrary, but fixed, finite set of points in the plane can be thought of as a generalized ellipse. Generalized conics with three foci are called trifocal ellipses. This can be further generalized to curves which are obtained as the loci of points such that some weighted sum
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is ...
of the distances from a finite set of points is a constant. A still further generalization is possible by assuming that the weights attached to the distances can be of arbitrary sign, namely, plus or minus. Finally, the restriction that the set of fixed points, called the set of foci of the generalized conic, be finite may also be removed. The set may be assumed to be finite or infinite. In the infinite case, the weighted arithmetic mean has to be replaced by an appropriate integral. Generalized conics in this sense are also called ''polyellipses'', ''egglipses'', or, ''generalized ellipses''. Since such curves were considered by the German mathematician Ehrenfried Walther von Tschirnhaus
Ehrenfried Walther von Tschirnhaus or Tschirnhauß (; 10 April 1651 – 11 October 1708) was a German mathematician, physicist, physician, and philosopher. He introduced the Tschirnhaus transformation and is considered by some to have been the ...
(1651 – 1708) they are also known as ''Tschirnhaus'sche Eikurve''. Also such generalizations have been discussed by René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
and by James Clerk Maxwell.
Multifocal oval curves


René Descartes
René Descartes ( , ; ; 31 March 1596 – 11 February 1650) was a French philosopher, scientist, and mathematician, widely considered a seminal figure in the emergence of modern philosophy and Modern science, science. Mathematics was paramou ...
in his ''La Géométrie
''La Géométrie'' () was published in 1637 as an appendix to ''Discours de la méthode'' ('' Discourse on the Method''), written by René Descartes. In the ''Discourse'', Descartes presents his method for obtaining clarity on any subject. ''La ...
'' (1637) set apart a section of about 15 pages to discuss what he called bifocal ellipses. A bifocal oval was defined there as the locus of a point ''P'' which moves in a plane such that where ''A'' and ''B'' are fixed points in the plane and ''λ'' and ''c'' are constants which may be positive or negative. Descartes introduced these ovals, which are now known as Cartesian ovals, to determine the surfaces of glass such that after refraction
In physics, refraction is the redirection of a wave as it passes from one transmission medium, medium to another. The redirection can be caused by the wave's change in speed or by a change in the medium. Refraction of light is the most commo ...
the rays meet at the same point. Descartes also recognized these ovals as generalizations of central conics, because for certain values of ''λ'' these ovals reduce to the familiar conics, namely, the circle, the ellipse or the hyperbola.
Multifocal ovals were rediscovered by James Clerk Maxwell
James Clerk Maxwell (13 June 1831 – 5 November 1879) was a Scottish physicist and mathematician who was responsible for the classical theory of electromagnetic radiation, which was the first theory to describe electricity, magnetism an ...
(1831–1879) while he was still a school student. At the age of 15, Maxwell wrote a scientific paper on these ovals with the title "Observations on circumscribed figures having a plurality of foci, and radii of various proportions". It was presented by James David Forbes
James David Forbes (1809–1868) was a Scottish physicist and glaciologist who worked extensively on the conduction of heat and seismology. Forbes was a resident of Edinburgh for most of his life, educated at its University and a professor ...
in a meeting of the Royal Society of Edinburgh
The Royal Society of Edinburgh (RSE) is Scotland's national academy of science and letters. It is a registered charity that operates on a wholly independent and non-partisan basis and provides public benefit throughout Scotland. It was establis ...
in 1846. Forbes also published an account of the paper in the ''Proceedings of the Royal Society of Edinburgh''. In his paper, though Maxwell did not use the term "generalized conic", he was considering curves which were generalizations of the defining condition of an ellipse.
Definition
A multifocal oval is a curve which is defined as the locus of a point moving such that : where ''A''1, ''A''2, . . . , ''A''''n'' are fixed points in a plane and ''λ''1, ''λ''2, . . . , ''λ''n are fixed rational numbers and ''c'' is a constant. He gave simple pin-string-pencil methods for drawing such ovals. The method for drawing the oval defined by the equation illustrates the general approach adopted by Maxwell for drawing such curves. Fix two pins at the foci ''A'' and ''B''. Take a string whose length is ''c'' + ''AB'' and tie one end of the string to the pin at ''A''. A pencil is attached to the other end of the string and the string is passed round the pin at the focus ''B''. The pencil is then moved guided by the bight of the string. The curve traced by the pencil is the locus of ''P''. His ingenuity is more visible in his description of the method for drawing a trifocal oval defined by an equation of the form . Let three pins be fixed at the three foci ''A'', ''B'', ''C''. Let one end of the string be fixed at the pin at ''C'' and let the string be passed around the other pins. Let the pencil be attached to the other end of the string. Let the pencil catch a bight in the string between ''A'' and ''C'' and then stretch to ''P''. The pencil is moved such that the string is taut. The resulting figure would be a part of a trifocal ellipse. The positions of the string may have to adjusted to get the full oval. In the two years after his paper was presented to the Royal Society of Edinburgh, Maxwell systematically developed the geometrical and optical properties of these ovals.Specialization and generalization of Maxwell's approach
As a special case of Maxwell's approach, consider the n-ellipse—the locus of a point which moves such that the following condition is satisfied: : Dividing by ''n'' and replacing ''c''/''n'' by ''c'', this defining condition can be stated as : This suggests a simple interpretation: the generalised conic is a curve such that the average distance of every point ''P'' on the curve from the set has the same constant value. This formulation of the concept of a generalized conic has been further generalised in several different ways. *''Change the definition of the average''. In the formulation, the average was interpreted as the arithmetic mean. This may be replaced by other notions of averages like geometric mean of the distances. If the geometric mean is used to specify the average, the resulting curves turn out to belemniscate
In algebraic geometry, a lemniscate ( or ) is any of several figure-eight or -shaped curves. The word comes from the Latin , meaning "decorated with ribbons", from the Greek (), meaning "ribbon",. or which alternatively may refer to the wool fr ...
s. "Lemniscates are sets all of whose points have the same geometric mean of the distances (i.e. their product is constant). Lemniscates play a central role in the theory of approximation. The polynomial approximation of a holomorphic function
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex de ...
can be interpreted as the approximation of the level curves with lemniscates. The product of distances corresponds to the absolute value of the root-decomposition of polynomials in the complex plane."
*''Change the cardinality
The thumb is the first digit of the hand, next to the index finger. When a person is standing in the medical anatomical position (where the palm is facing to the front), the thumb is the outermost digit. The Medical Latin English noun for thum ...
of the focal set''. Modify the definition so that the definition can be applied even in the case where the focal set infinite. This possibility was first introduced by C. Gross and T.-K. Strempel and they posed the problem whether which results (of the classical case) can be extended to the case of infinitely many focal points or to continuous set of foci.
*''Change the dimension of the underlying space''. The points may be assumed to lie in some ''d''-dimensional space.
*''Change the definition of the distance''. Traditionally euclidean definitions are employed. in its place, other notions of distance like taxicab distance, may be used. Generalized conics with this notion of distance have found applications in geometric tomography
Tomography is imaging by sections or sectioning that uses any kind of penetrating wave. The method is used in radiology, archaeology, biology, atmospheric science, geophysics, oceanography, plasma physics, materials science, cosmochemistry, ast ...
.
The formulation of the definition of the generalized conic in the most general case when the cardinality of the focal set is infinite involves the notions of measurable sets and Lebesgue integration
In mathematics, the integral of a non-negative function of a single variable can be regarded, in the simplest case, as the area between the graph of that function and the axis. The Lebesgue integral, named after French mathematician Henri L ...
. All these have been employed by different authors and the resulting curves have been studied with special emphasis on applications.
Definition
Let be a metric and a measure on a compact set with . The unweighted generalized conic function associated with is : where is a kernel function associated with . is the set of foci. The level sets are called generalized conics.Generalized conics via polar equations

 Given a conic, by choosing a
Given a conic, by choosing a focus
Focus (: foci or focuses) may refer to:
Arts
* Focus or Focus Festival, former name of the Adelaide Fringe arts festival in East Australia Film
*Focus (2001 film), ''Focus'' (2001 film), a 2001 film based on the Arthur Miller novel
*Focus (2015 ...
of the conic as the pole and the line through the pole drawn parallel to the directrix of the conic as the polar axis, the polar equation of the conic
A conic section, conic or a quadratic curve is a curve obtained from a cone's surface intersecting a plane. The three types of conic section are the hyperbola, the parabola, and the ellipse; the circle is a special case of the ellipse, thou ...
can be written in the following form:
:
Here ''e'' is the eccentricity
Eccentricity or eccentric may refer to:
* Eccentricity (behavior), odd behavior on the part of a person, as opposed to being "normal"
Mathematics, science and technology Mathematics
* Off-Centre (geometry), center, in geometry
* Eccentricity (g ...
of the conic and ''d'' is the distance of the directrix from the pole. Tom M. Apostol and Mamikon A. Mnatsakanian in their study of curves drawn on the surfaces of right circular cones introduced a new class of curves which they called generalized conics. These are curves whose polar equations are similar to the polar equations of ordinary conics and the ordinary conics appear as special cases of these generalized conics.
Definition
For constants ''r''0 ≥ 0, ''λ'' ≥ 0 and real ''k'', a plane curve described by the polar equation : is called a ''generalized conic''. The conic is called a generalized ellipse, parabola or hyperbola according as ''λ'' < 1, ''λ'' = 1, or ''λ'' > 1.Special cases
*In the special case when ''k'' = 1, the generalized conic reduces to an ordinary conic. *In the special case when ''k'' > 1, there is a simple geometrical method for the generation of the corresponding generalized conic. ::Let ''α'' be an angle such that sin ''α'' = 1/''k''. Consider a right circular cone with semi-vertical angle equal to ''α''. Consider the intersection of this cone by a plane such that the intersection is a conic with eccentricity ''λ''. Unwrap the cone to a plane. Then the curve in the plane to which the conic section of eccentricity ''λ'' is unwrapped is a generalized conic with polar equation as specified in the definition. *In the special case when ''k'' < 1, the generalized conic cannot be obtained by unwrapping a conic section. In this case there is another interpretation. ::Consider an ordinary conic drawn on a plane. Wrap the plane to form a right circular cone so that the conic becomes a curve in three-dimensional space. The projection of the curve onto a plane perpendicular to the axis of the cone will be a generalized conic in the sense of Apostol and Mnatsakanian with ''k'' < 1.Examples
Generalized conics in curve approximation
In 1996, Ruibin Qu introduced a new notion of generalized conic as a tool for generating approximations to curves. The starting point for this generalization is the result that the sequence of points defined by : lie on a conic. In this approach, the generalized conic is now defined as below.Definition
A generalized conic is such a curve that if the two points and are on it, then the points generated by the recursive relation : for some and satisfying the relations : are also on it.Generalized conics as equidistant sets

Definition
Let (''X'', ''d'') be ametric space
In mathematics, a metric space is a Set (mathematics), set together with a notion of ''distance'' between its Element (mathematics), elements, usually called point (geometry), points. The distance is measured by a function (mathematics), functi ...
and let ''A'' be a nonempty
In mathematics, the empty set or void set is the unique set having no elements; its size or cardinality (count of elements in a set) is zero. Some axiomatic set theories ensure that the empty set exists by including an axiom of empty set, whi ...
subset of ''X''. If ''x'' is a point in ''X'', the distance of ''x'' from ''A'' is defined as ''d''(''x'', ''A'') = inf. If ''A'' and ''B'' are both nonempty subsets of ''X'' then the equidistant set determined by ''A'' and ''B'' is defined to be the set . This equidistant set is denoted by . The term generalized conic is used to denote a general equidistant set.
Examples
Classical conics can be realized as equidistant sets. For example, if ''A'' is a singleton set and ''B'' is a straight line, then the equidistant set is a parabola. If ''A'' and ''B'' are circles such that ''A'' is completely within ''B'' then the equidistant set is an ellipse. On the other hand, if ''A'' lies completely outside ''B'' the equidistant set is a hyperbola. A similar approach considers a generalization of the focus/directrix/eccentricity interpretation of conics, by retaining a single point ''F'' for the focus, any differentiable curve ''d'' serving as the directrix, and ''e'' > 0, the eccentricity. Let ''X'' be a variable point on d. The resultant generalized conic is the set of points ''P'' (each lying on a normal to ''d'' through ''X'') for which the distances ''PF'' and ''PX'' satisfy the ratio ''PF/PX = e''. Norman and Poplin referred to these curves as pseudoconics and the constraint that the distance from ''P'' to the directrix be minimal has been discarded. If one retains the minimality requirement, then the set of points ''P'' satisfying this requirement are considered to be the primary pseudoconic, and the remainder of the curve is the secondary branch of the pseudoconic. Similar examples of generalized parabolas can be found in Joseph ''et al.''.
If one retains the minimality requirement, then the set of points ''P'' satisfying this requirement are considered to be the primary pseudoconic, and the remainder of the curve is the secondary branch of the pseudoconic. Similar examples of generalized parabolas can be found in Joseph ''et al.''.References
Further reading
*For a detailed discussion of generalized conics from the viewpoint of differential geometry, see the chapter on generalized conics in the book Convex Geometry by Csaba Vincze available online.{{cite web, last1=Csaba Vincze, title=Convex Geometry Chapter 10. Generalized Conics, url=http://www.tankonyvtar.hu/en/tartalom/tamop412A/2011_0025_mat_14/ch10.html, website=Digitalis Tankonyvtar, accessdate=17 December 2015 Conic sections Algebraic curves