|
Weighted Sum
A weight function is a mathematical device used when performing a sum, integral, or average to give some elements more "weight" or influence on the result than other elements in the same set. The result of this application of a weight function is a weighted sum or weighted average. Weight functions occur frequently in statistics and analysis, and are closely related to the concept of a measure. Weight functions can be employed in both discrete and continuous settings. They can be used to construct systems of calculus called "weighted calculus" and "meta-calculus".Jane Grossma''Meta-Calculus: Differential and Integral'' , 1981. Discrete weights General definition In the discrete setting, a weight function w \colon A \to \R^+ is a positive function defined on a discrete set A, which is typically finite or countable. The weight function w(a) := 1 corresponds to the ''unweighted'' situation in which all elements have equal weight. One can then apply this weight to various conc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weighted Average
The weighted arithmetic mean is similar to an ordinary arithmetic mean (the most common type of average), except that instead of each of the data points contributing equally to the final average, some data points contribute more than others. The notion of weighted mean plays a role in descriptive statistics and also occurs in a more general form in several other areas of mathematics. If all the weights are equal, then the weighted mean is the same as the arithmetic mean. While weighted means generally behave in a similar fashion to arithmetic means, they do have a few counterintuitive properties, as captured for instance in Simpson's paradox. Examples Basic example Given two school with 20 students, one with 30 test grades in each class as follows: :Morning class = :Afternoon class = The mean for the morning class is 80 and the mean of the afternoon class is 90. The unweighted mean of the two means is 85. However, this does not account for the difference in number of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bias (statistics)
In the field of statistics, bias is a systematic tendency in which the methods used to gather data and estimate a sample statistic present an inaccurate, skewed or distorted ('' biased'') depiction of reality. Statistical bias exists in numerous stages of the data collection and analysis process, including: the source of the data, the methods used to collect the data, the estimator chosen, and the methods used to analyze the data. Data analysts can take various measures at each stage of the process to reduce the impact of statistical bias in their work. Understanding the source of statistical bias can help to assess whether the observed results are close to actuality. Issues of statistical bias has been argued to be closely linked to issues of statistical validity. Statistical bias can have significant real world implications as data is used to inform decision making across a wide variety of processes in society. Data is used to inform lawmaking, industry regulation, corp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
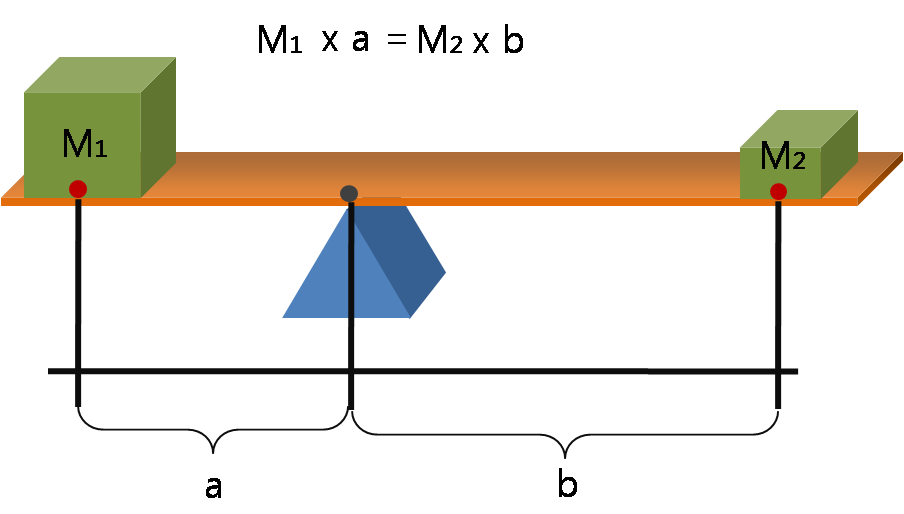
Lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load, and effort, the lever is divided into Lever#Types of levers, three types. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English language, English around 1300 from . This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to , itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The word's primary origin is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Weight
In science and engineering, the weight of an object is a quantity associated with the gravitational force exerted on the object by other objects in its environment, although there is some variation and debate as to the exact definition. Some standard textbooks define weight as a Euclidean vector, vector quantity, the gravitational force acting on the object. Others define weight as a scalar quantity, the magnitude of the gravitational force. Yet others define it as the magnitude of the reaction (physics), reaction force exerted on a body by mechanisms that counteract the effects of gravity: the weight is the quantity that is measured by, for example, a spring scale. Thus, in a state of free fall, the weight would be zero. In this sense of weight, terrestrial objects can be weightless: so if one ignores Drag (physics), air resistance, one could say the legendary apple falling from the tree, on its way to meet the ground near Isaac Newton, was weightless. The unit of measurement fo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lever
A lever is a simple machine consisting of a beam (structure), beam or rigid rod pivoted at a fixed hinge, or '':wikt:fulcrum, fulcrum''. A lever is a rigid body capable of rotating on a point on itself. On the basis of the locations of fulcrum, load, and effort, the lever is divided into Lever#Types of levers, three types. It is one of the six simple machines identified by Renaissance scientists. A lever amplifies an input force to provide a greater output force, which is said to provide leverage, which is mechanical advantage gained in the system, equal to the ratio of the output force to the input force. As such, the lever is a mechanical advantage device, trading off force against movement. Etymology The word "lever" entered English language, English around 1300 from . This sprang from the stem of the verb ''lever'', meaning "to raise". The verb, in turn, goes back to , itself from the adjective ''levis'', meaning "light" (as in "not heavy"). The word's primary origin is the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanics
Mechanics () is the area of physics concerned with the relationships between force, matter, and motion among Physical object, physical objects. Forces applied to objects may result in Displacement (vector), displacements, which are changes of an object's position relative to its environment. Theoretical expositions of this branch of physics has its origins in Ancient Greece, for instance, in the writings of Aristotle and Archimedes (see History of classical mechanics and Timeline of classical mechanics). During the early modern period, scientists such as Galileo Galilei, Johannes Kepler, Christiaan Huygens, and Isaac Newton laid the foundation for what is now known as classical mechanics. As a branch of classical physics, mechanics deals with bodies that are either at rest or are moving with velocities significantly less than the speed of light. It can also be defined as the physical science that deals with the motion of and forces on bodies not in the quantum realm. History ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Moving Average Model
In time series analysis, the moving-average model (MA model), also known as moving-average process, is a common approach for modeling univariate time series. The moving-average model specifies that the output variable is cross-correlated with a non-identical to itself random-variable. Together with the autoregressive (AR) model, the moving-average model is a special case and key component of the more general ARMA and ARIMA models of time series, which have a more complicated stochastic structure. Contrary to the AR model, the finite MA model is always stationary. The moving-average model should not be confused with the moving average, a distinct concept despite some similarities. Definition The notation MA(''q'') refers to the moving average model of order ''q'': : X_t = \mu + \varepsilon_t + \theta_1 \varepsilon_ + \cdots + \theta_q \varepsilon_ = \mu + \sum_^q \theta_i \varepsilon_ + \varepsilon_, where \mu is the mean of the series, the \theta_1,...,\theta_q are the co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Distributed Lag
Distribution may refer to: Mathematics *Distribution (mathematics), generalized functions used to formulate solutions of partial differential equations *Probability distribution, the probability of a particular value or value range of a variable **Cumulative distribution function, in which the probability of being no greater than a particular value is a function of that value *Frequency distribution, a list of the values recorded in a sample * Inner distribution, and outer distribution, in coding theory *Distribution (differential geometry), a subset of the tangent bundle of a manifold * Distributed parameter system, systems that have an infinite-dimensional state-space * Distribution of terms, a situation in which all members of a category are accounted for *Distributivity, a property of binary operations that generalises the distributive law from elementary algebra *Distribution (number theory) *Distribution problems, a common type of problems in combinatorics where the goa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Independent Variable
A variable is considered dependent if it depends on (or is hypothesized to depend on) an independent variable. Dependent variables are studied under the supposition or demand that they depend, by some law or rule (e.g., by a mathematical function), on the values of other variables. Independent variables, on the other hand, are not seen as depending on any other variable in the scope of the experiment in question. Rather, they are controlled by the experimenter. In pure mathematics In mathematics, a function is a rule for taking an input (in the simplest case, a number or set of numbers)Carlson, Robert. A concrete introduction to real analysis. CRC Press, 2006. p.183 and providing an output (which may also be a number). A symbol that stands for an arbitrary input is called an independent variable, while a symbol that stands for an arbitrary output is called a dependent variable. The most common symbol for the input is , and the most common symbol for the output is ; the function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Regression
In statistics, linear regression is a statistical model, model that estimates the relationship between a Scalar (mathematics), scalar response (dependent variable) and one or more explanatory variables (regressor or independent variable). A model with exactly one explanatory variable is a ''simple linear regression''; a model with two or more explanatory variables is a multiple linear regression. This term is distinct from multivariate linear regression, which predicts multiple correlated dependent variables rather than a single dependent variable. In linear regression, the relationships are modeled using linear predictor functions whose unknown model parameters are estimation theory, estimated from the data. Most commonly, the conditional mean of the response given the values of the explanatory variables (or predictors) is assumed to be an affine function of those values; less commonly, the conditional median or some other quantile is used. Like all forms of regression analysis, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is a branch of mathematics and statistics concerning events and numerical descriptions of how likely they are to occur. The probability of an event is a number between 0 and 1; the larger the probability, the more likely an event is to occur."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th ed., (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', vol. 1, 3rd ed., (1968), Wiley, . This number is often expressed as a percentage (%), ranging from 0% to 100%. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written as 0.5 or 50%). These concepts have been given an axiomatic mathematical formaliza ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |