Froude number

In continuum mechanics, the Froude number (, after William Froude, ) is a dimensionless number defined as the ratio of the flow inertia to the external field (the latter in many applications simply due to gravity). The Froude number is based on the speed–length ratio which he defined as:
$\mathrm = \frac$
where is the local flow velocity, is the local external field, and is a characteristic length. The Froude number has some analogy with the Mach number. In theoretical fluid dynamics the Froude number is not frequently considered since usually the equations are considered in the high Froude limit of negligible external field, leading to homogeneous equations that preserve the mathematical aspects. For example, homogeneous Euler equations are conservation equations.

However, in naval architecture the Froude number is a significant figure used to determine the resistance of a partially submerged object moving through water.

Origins

In open channel flows, introduced first the ratio of the flow velocity to the square root of the gravity acceleration times the flow depth. When the ratio was less than unity, the flow behaved like a fluvial motion (i.e., subcritical flow), and like a torrential flow motion when the ratio was greater than unity.

Quantifying resistance of floating objects is generally credited to William Froude, who used a series of scale models to measure the resistance each model offered when towed at a given speed. The naval constructor Frederic Reech had put forward the concept much earlier in 1852 for testing ships and propellers but Froude was unaware of it. Speed–length ratio was originally defined by Froude in his ''Law of Comparison'' in 1868 in dimensional terms as:
$\text =\frac$
where:
* = flow speed
* = length of waterline

The term was converted into non-dimensional terms and was given Froude's name in recognition of the work he did. In France, it is sometimes called Reech–Froude number after Frederic Reech.

Definition and main application

To show how the Froude number is linked to general continuum mechanics and not only to hydrodynamics we start from the Cauchy momentum equation in its dimensionless (nondimensional) form.

Cauchy momentum equation

In order to make the equations dimensionless, a characteristic length r₀, and a characteristic velocity u₀, need to be defined. These should be chosen such that the dimensionless variables are all of order one. The following dimensionless variables are thus obtained:
$\rho^*\equiv \frac \rho , \quad u^*\equiv \frac u , \quad r^*\equiv \frac r , \quad t^*\equiv \frac t, \quad \nabla^*\equiv r_0 \nabla , \quad \mathbf g^* \equiv \frac , \quad \boldsymbol \sigma^* \equiv \frac ,$

Substitution of these inverse relations in the Euler momentum equations, and definition of the Froude number:
$\mathrm=\frac,$
and the Euler number:
$\mathrm=\frac,$
the equations are finally expressed (with the material derivative and now omitting the indexes):

Cauchy-type equations in the high Froude limit (corresponding to negligible external field) are named free equations. On the other hand, in the low Euler limit (corresponding to negligible stress) general Cauchy momentum equation becomes an inhomogeneous Burgers equation (here we make explicit the material derivative):

This is an inhomogeneous pure advection equation, as much as the Stokes equation is a pure diffusion equation.

Euler momentum equation

Euler momentum equation is a Cauchy momentum equation with the Pascal law being the stress constitutive relation:
$\boldsymbol \sigma = p \mathbf I$
in nondimensional Lagrangian form is:
$\frac + \mathrm \frac = \frac 1 \hat g$

Free Euler equations are conservative. The limit of high Froude numbers (low external field) is thus notable and can be studied with perturbation theory.

Incompressible Navier–Stokes momentum equation

Incompressible Navier–Stokes momentum equation is a Cauchy momentum equation with the Pascal law and Stokes's law being the stress constitutive relations:
$\boldsymbol \sigma = p \mathbf I + \mu \left(\nabla\mathbf + ( \nabla\mathbf )^\mathsf\right)$
in nondimensional convective form it is:
$\frac + \mathrm \frac = \frac 1 \nabla^2 u + \frac 1 \hat g$
where is the Reynolds number. Free Navier–Stokes equations are dissipative (non conservative).

Other applications

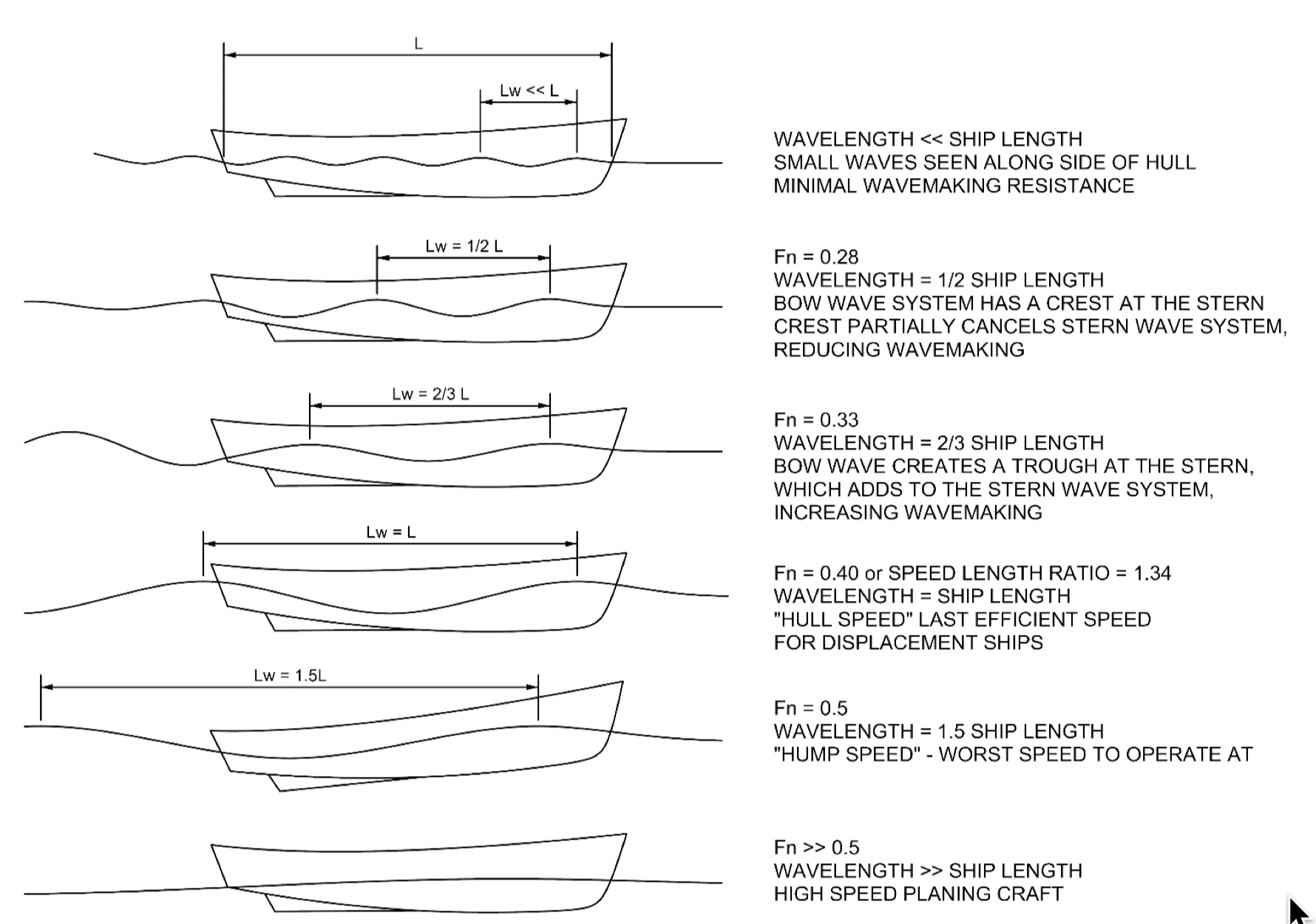
Ship hydrodynamics

In marine hydrodynamic applications, the Froude number is usually referenced with the notation and is defined as:
$\mathrm_L = \frac,$
where is the relative flow velocity between the sea and ship, is in particular the acceleration due to gravity, and is the length of the ship at the water line level, or in some notations. It is an important parameter with respect to the ship's drag, or resistance, especially in terms of wave making resistance.

In the case of planing crafts, where the waterline length is too speed-dependent to be meaningful, the Froude number is best defined as ''displacement Froude number'' and the reference length is taken as the cubic root of the volumetric displacement of the hull:
$\mathrm_V = \frac.$

Shallow water waves

For shallow water waves, such as tsunamis and hydraulic jumps, the characteristic velocity is the average flow velocity, averaged over the cross-section perpendicular to the flow direction. The wave velocity, termed celerity , is equal to the square root of gravitational acceleration , times cross-sectional area , divided by free-surface width :
$c = \sqrt,$
so the Froude number in shallow water is:
$\mathrm = \frac.$
For rectangular cross-sections with uniform depth , the Froude number can be simplified to:
$\mathrm = \frac.$
For the flow is called a subcritical flow, further for the flow is characterised as supercritical flow. When the flow is denoted as critical flow.

Wind engineering

When considering wind effects on dynamically sensitive structures such as suspension bridges it is sometimes necessary to simulate the combined effect of the vibrating mass of the structure with the fluctuating force of the wind. In such cases, the Froude number should be respected.
Similarly, when simulating hot smoke plumes combined with natural wind, Froude number scaling is necessary to maintain the correct balance between buoyancy forces and the momentum of the wind.

Allometry

The Froude number has also been applied in allometry to studying the locomotion of terrestrial animals, including antelope and dinosaurs.

Extended Froude number

Geophysical mass flows such as avalanches and debris flows take place on inclined slopes which then merge into gentle and flat run-out zones.

So, these flows are associated with the elevation of the topographic slopes that induce the gravity potential energy together with the pressure potential energy during the flow. Therefore, the classical Froude number should include this additional effect. For such a situation, Froude number needs to be re-defined. The extended Froude number is defined as the ratio between the kinetic and the potential energy:
$\mathrm = \frac,$
where is the mean flow velocity, , ( is the earth pressure coefficient, is the slope), , is the channel downslope position and $x_d$ is the distance from the point of the mass release along the channel to the point where the flow hits the horizontal reference datum; and are the pressure potential and gravity potential energies, respectively. In the classical definition of the shallow-water or granular flow Froude number, the potential energy associated with the surface elevation, , is not considered. The extended Froude number differs substantially from the classical Froude number for higher surface elevations. The term emerges from the change of the geometry of the moving mass along the slope. Dimensional analysis suggests that for shallow flows , while and are both of order unity. If the mass is shallow with a virtually bed-parallel free-surface, then can be disregarded. In this situation, if the gravity potential is not taken into account, then is unbounded even though the kinetic energy is bounded. So, formally considering the additional contribution due to the gravitational potential energy, the singularity in Fr is removed.

Stirred tanks

In the study of stirred tanks, the Froude number governs the formation of surface vortices. Since the impeller tip velocity is (circular motion), where is the impeller frequency (usually in rpm) and is the impeller radius (in engineering the diameter is much more frequently employed), the Froude number then takes the following form:
$\mathrm=\omega \sqrt \frac.$
The Froude number finds also a similar application in powder mixers. It will indeed be used to determine in which mixing regime the blender is working. If Fr<1, the particles are just stirred, but if Fr>1, centrifugal forces applied to the powder overcome gravity and the bed of particles becomes fluidized, at least in some part of the blender, promoting mixing

Densimetric Froude number

When used in the context of the Boussinesq approximation the densimetric Froude number is defined as
$\mathrm=\frac$
where is the reduced gravity:
$g' = g\frac$

The densimetric Froude number is usually preferred by modellers who wish to nondimensionalize a speed preference to the Richardson number which is more commonly encountered when considering stratified shear layers. For example, the leading edge of a gravity current moves with a front Froude number of about unity.

Walking Froude number

The Froude number may be used to study trends in animal gait patterns. In analyses of the dynamics of legged locomotion, a walking limb is often modeled as an inverted pendulum, where the center of mass goes through a circular arc centered at the foot. The Froude number is the ratio of the centripetal force around the center of motion, the foot, and the weight of the animal walking:
$\mathrm=\frac=\frac = \frac$
where is the mass, is the characteristic length, is the acceleration due to gravity and is the velocity. The characteristic length may be chosen to suit the study at hand. For instance, some studies have used the vertical distance of the hip joint from the ground, while others have used total leg length.

The Froude number may also be calculated from the stride frequency as follows:
$\mathrm=\frac=\frac=\frac.$

If total leg length is used as the characteristic length, then the theoretical maximum speed of walking has a Froude number of 1.0 since any higher value would result in takeoff and the foot missing the ground. The typical transition speed from bipedal walking to running occurs with . R. M. Alexander found that animals of different sizes and masses travelling at different speeds, but with the same Froude number, consistently exhibit similar gaits. This study found that animals typically switch from an amble to a symmetric running gait (e.g., a trot or pace) around a Froude number of 1.0. A preference for asymmetric gaits (e.g., a canter, transverse gallop, rotary gallop, bound, or pronk) was observed at Froude numbers between 2.0 and 3.0.

Usage

The Froude number is used to compare the wave making resistance between bodies of various sizes and shapes.

In free-surface flow, the nature of the flow ( supercritical or subcritical) depends upon whether the Froude number is greater than or less than unity.

One can easily see the line of "critical" flow in a kitchen or bathroom sink. Leave it unplugged and let the faucet run. Near the place where the stream of water hits the sink, the flow is supercritical. It 'hugs' the surface and moves quickly. On the outer edge of the flow pattern the flow is subcritical. This flow is thicker and moves more slowly. The boundary between the two areas is called a "hydraulic jump". The jump starts where the flow is just critical and Froude number is equal to 1.0.

The Froude number has been used to study trends in animal locomotion in order to better understand why animals use different gait patterns as well as to form hypotheses about the gaits of extinct species.

In addition particle bed behavior can be quantified by Froude number (Fr) in order to establish the optimum operating window.

See also

*
*
*
*
*
*

Notes

References

*
*
*
*
*
*
*
*
*
*
*
*
*

External links

* https://web.archive.org/web/20070927085042/http://www.qub.ac.uk/waves/fastferry/reference/MCA457.pdf

{{NonDimFluMech

Dimensionless numbers of fluid mechanics
Fluid dynamics
Naval architecture