|
Burgers Equation
Burgers' equation or Bateman–Burgers equation is a fundamental partial differential equation and convection–diffusion equation occurring in various areas of applied mathematics, such as fluid mechanics, nonlinear acoustics, gas dynamics, and traffic flow. The equation was first introduced by Harry Bateman in 1915 and later studied by Johannes Martinus Burgers in 1948. For a given field u(x,t) and diffusion coefficient (or ''kinematic viscosity'', as in the original fluid mechanical context) \nu, the general form of Burgers' equation (also known as viscous Burgers' equation) in one space dimension is the dissipative system: \frac + u \frac = \nu\frac. When the diffusion term is absent (i.e. \nu=0), Burgers' equation becomes the inviscid Burgers' equation: \frac + u \frac = 0, which is a prototype for conservation equations that can develop discontinuities (shock waves). The previous equation is the ''advective form'' of the Burgers' equation. The ''conservative form'' is found t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equation
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a Multivariable calculus, multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to Numerical methods for partial differential equations, numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematics, pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hyperbolic Equation
In mathematics, a hyperbolic partial differential equation of order n is a partial differential equation (PDE) that, roughly speaking, has a well-posed initial value problem for the first n-1 derivatives. More precisely, the Cauchy problem can be locally solved for arbitrary initial data along any non-characteristic hypersurface. Many of the equations of mechanics are hyperbolic, and so the study of hyperbolic equations is of substantial contemporary interest. The model hyperbolic equation is the wave equation. In one spatial dimension, this is : \frac = c^2 \frac The equation has the property that, if ''u'' and its first time derivative are arbitrarily specified initial data on the line (with sufficient smoothness properties), then there exists a solution for all time ''t''. The solutions of hyperbolic equations are "wave-like". If a disturbance is made in the initial data of a hyperbolic differential equation, then not every point of space feels the disturbance at once. Rela ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fokker–Planck Equation
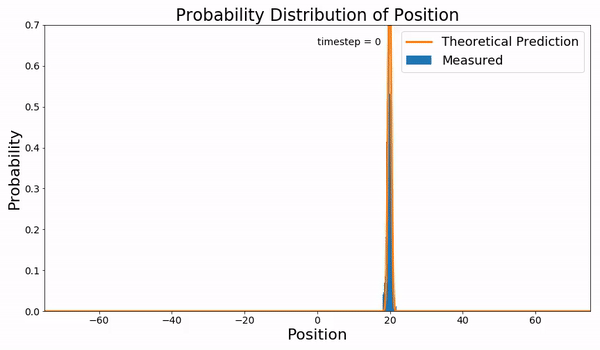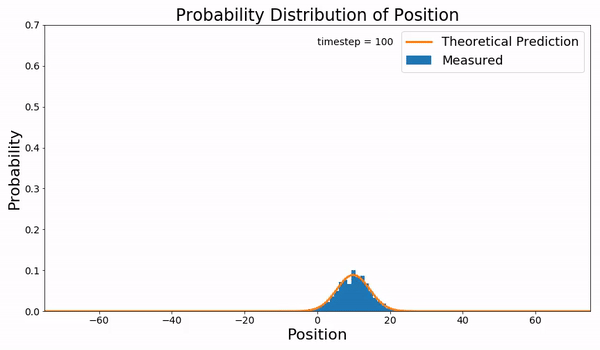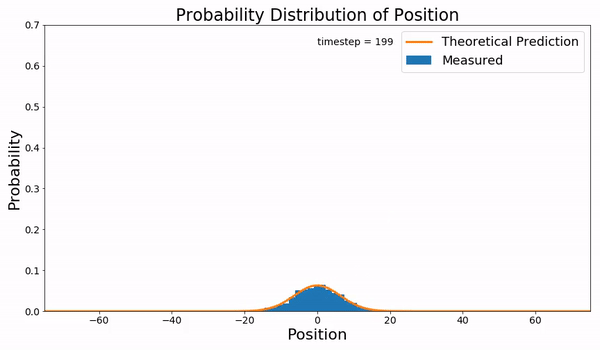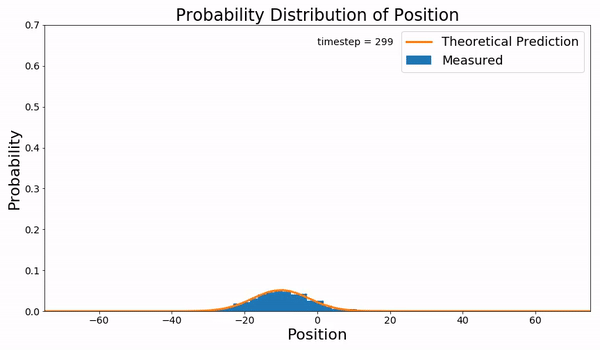
In statistical mechanics, the Fokker–Planck equation is a partial differential equation that describes the time evolution of the probability density function of the velocity of a particle under the influence of drag forces and random forces, as in Brownian motion. The equation can be generalized to other observables as well. It is named after Adriaan Fokker and Max Planck, who described it in 1914 and 1917. It is also known as the Kolmogorov forward equation, after Andrey Kolmogorov, who independently discovered it in 1931. When applied to particle position distributions, it is better known as the Smoluchowski equation (after Marian Smoluchowski), and in this context it is equivalent to the convection–diffusion equation. The case with zero diffusion is the continuity equation. The Fokker–Planck equation is obtained from the master equation through Kramers–Moyal expansion. The first consistent microscopic derivation of the Fokker–Planck equation in the single schem ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Conservation Law
In physics, a conservation law states that a particular measurable property of an isolated physical system does not change as the system evolves over time. Exact conservation laws include conservation of energy, conservation of linear momentum, conservation of angular momentum, and conservation of electric charge. There are also many approximate conservation laws, which apply to such quantities as mass, parity, lepton number, baryon number, strangeness, hypercharge, etc. These quantities are conserved in certain classes of physics processes, but not in all. A local conservation law is usually expressed mathematically as a continuity equation, a partial differential equation which gives a relation between the amount of the quantity and the "transport" of that quantity. It states that the amount of the conserved quantity at a point or within a volume can only change by the amount of the quantity which flows in or out of the volume. From Noether's theorem, each conservation la ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaplygin's Equation
In gas dynamics, Chaplygin's equation, named after Sergei Alekseevich Chaplygin (1902), is a partial differential equation useful in the study of transonic flow. It is : \frac + \frac\frac+v \frac=0. Here, c=c(v) is the speed of sound, determined by the equation of state of the fluid and conservation of energy. For polytropic gases, we have c^2/(\gamma-1) = h_0- v^2/2, where \gamma is the specific heat ratio and h_0 is the stagnation enthalpy, in which case the Chaplygin's equation reduces to : \frac + v^2\frac\frac+v \frac=0. The Bernoulli equation (see the derivation below) states that maximum velocity occurs when specific enthalpy is at the smallest value possible; one can take the specific enthalpy to be zero corresponding to absolute zero temperature as the reference value, in which case 2h_0 is the maximum attainable velocity. The particular integrals of above equation can be expressed in terms of hypergeometric functions. Derivation For two-dimensional potential flow, th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euler–Tricomi Equation
In mathematics, the Euler–Tricomi equation is a linear partial differential equation useful in the study of transonic flow. It is named after mathematicians Leonhard Euler and Francesco Giacomo Tricomi. : u_+xu_=0. \, It is elliptic in the half plane ''x'' > 0, parabolic at ''x'' = 0 and hyperbolic in the half plane ''x'' < 0. Its characteristics are : which have the integral : where ''C'' is a constant of . The characteristics thus comprise two families of s, with cusps on the line ''x'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solving The Heat Equation Using Fourier Series
In mathematics and physics, the heat equation is a certain partial differential equation. Solutions of the heat equation are sometimes known as caloric functions. The theory of the heat equation was first developed by Joseph Fourier in 1822 for the purpose of modeling how a quantity such as heat diffuses through a given region. As the prototypical parabolic partial differential equation, the heat equation is among the most widely studied topics in pure mathematics, and its analysis is regarded as fundamental to the broader field of partial differential equations. The heat equation can also be considered on Riemannian manifolds, leading to many geometric applications. Following work of Subbaramiah Minakshisundaram and Åke Pleijel, the heat equation is closely related with spectral geometry. A seminal nonlinear variant of the heat equation was introduced to differential geometry by James Eells and Joseph Sampson in 1964, inspiring the introduction of the Ricci flow by Richard H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cole–Hopf Transformation
The Cole–Hopf transformation is a method of solving parabolic partial differential equations (PDEs) with a quadratic nonlinearity of the form:u_ - a\Delta u + b\, \nabla u\, ^ = 0, \quad u(0,x) = g(x) where x\in \mathbb^, a,b are constants, \Delta is the Laplace operator, \nabla is the gradient, and \, \cdot\, ^ is the \ell^-norm. By assuming that w = \phi(u), where \phi(\cdot) is an unknown smooth function, we may calculate:w_ = \phi'(u)u_, \quad \Delta w = \phi'(u)\Delta u + \phi''(u)\, \nabla u\, ^ Which implies that:\begin w_ = \phi'(u)u_ &= \phi'(u)\left( a\Delta u - b\, \nabla u\, ^\right) \\ &= a\Delta w - (a\phi'' + b\phi')\, \nabla u\, ^ \\ &= a\Delta w \end if we constrain \phi to satisfy a\phi'' + b\phi' = 0. Then we may transform the original nonlinear PDE into the canonical heat equation by using the transformation: This is ''the'' ''Cole-Hopf transformation''. With the transformation, the following initial-value problem can now be solved:w_ - a\Delta w = 0, \quad w(0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Solution Of The Viscous Two Dimensional Burgers Equation
*
{{disambiguation ...
Solution may refer to: * Solution (chemistry), a mixture where one substance is dissolved in another * Solution (equation), in mathematics ** Numerical solution, in numerical analysis, approximate solutions within specified error bounds * Solution, in problem solving * Solution, in solution selling Other uses * V-STOL Solution, an ultralight aircraft * Solution (band), a Dutch rock band ** ''Solution'' (Solution album), 1971 * Solution A.D., an American rock band * ''Solution'' (Cui Jian album), 1991 * ''Solutions'' (album), a 2019 album by K.Flay See also * The Solution (other) The Solution may refer to: * ''The Solution'' (Mannafest album), an album by indie rock band Mannafest * ''The Solution'' (Beanie Sigel album), an album by rapper Beanie Sigel * ''The Solution'' (Buckshot and 9th Wonder album), a collaboration albu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
First-order Partial Differential Equation
In mathematics, a first-order partial differential equation is a partial differential equation that involves only first derivatives of the unknown function of ''n'' variables. The equation takes the form : F(x_1,\ldots,x_n,u,u_,\ldots u_) =0. \, Such equations arise in the construction of characteristic surfaces for hyperbolic partial differential equations, in the calculus of variations, in some geometrical problems, and in simple models for gas dynamics whose solution involves the method of characteristics. If a family of solutions of a single first-order partial differential equation can be found, then additional solutions may be obtained by forming envelopes of solutions in that family. In a related procedure, general solutions may be obtained by integrating families of ordinary differential equations. General solution and complete integral The ''general solution'' to the first order partial differential equation is a solution which contains an arbitrary function. But, the sol ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |