Epimorphic on:
[Wikipedia]
[Google]
[Amazon]
In
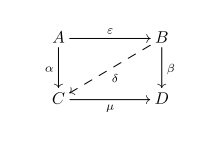 An epimorphism is said to be strong if for any monomorphism and any morphisms and such that , there exists a morphism such that and .
* An epimorphism is said to be split if there exists a morphism such that (in this case is called a right-sided inverse for ).
There is also the notion of homological epimorphism in ring theory. A morphism ''f'': ''A'' → ''B'' of rings is a homological epimorphism if it is an epimorphism and it induces a full and faithful functor on derived categories:
D(''f'') : D(''B'') → D(''A'').
A morphism that is both a monomorphism and an epimorphism is called a bimorphism. Every isomorphism is a bimorphism but the converse is not true in general. For example, the map from the half-open interval ,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane">unit circle">,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane) that sends ''x'' to exp(2πi''x'') (see Euler's formula) is continuous and bijective but not a homeomorphism since the inverse map is not continuous at 1, so it is an instance of a bimorphism that is not an isomorphism in the category Top. Another example is the embedding Q → R in the category Haus; as noted above, it is a bimorphism, but it is not bijective and therefore not an isomorphism. Similarly, in the category of rings, the map Z → Q is a bimorphism but not an isomorphism.
Epimorphisms are used to define abstract
An epimorphism is said to be strong if for any monomorphism and any morphisms and such that , there exists a morphism such that and .
* An epimorphism is said to be split if there exists a morphism such that (in this case is called a right-sided inverse for ).
There is also the notion of homological epimorphism in ring theory. A morphism ''f'': ''A'' → ''B'' of rings is a homological epimorphism if it is an epimorphism and it induces a full and faithful functor on derived categories:
D(''f'') : D(''B'') → D(''A'').
A morphism that is both a monomorphism and an epimorphism is called a bimorphism. Every isomorphism is a bimorphism but the converse is not true in general. For example, the map from the half-open interval ,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane">unit circle">,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane) that sends ''x'' to exp(2πi''x'') (see Euler's formula) is continuous and bijective but not a homeomorphism since the inverse map is not continuous at 1, so it is an instance of a bimorphism that is not an isomorphism in the category Top. Another example is the embedding Q → R in the category Haus; as noted above, it is a bimorphism, but it is not bijective and therefore not an isomorphism. Similarly, in the category of rings, the map Z → Q is a bimorphism but not an isomorphism.
Epimorphisms are used to define abstract
category theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, cate ...
, an epimorphism (also called an epic morphism or, colloquially, an epi) is a morphism
In mathematics, particularly in category theory, a morphism is a structure-preserving map from one mathematical structure to another one of the same type. The notion of morphism recurs in much of contemporary mathematics. In set theory, morphisms a ...
''f'' : ''X'' → ''Y'' that is right-cancellative in the sense that, for all objects ''Z'' and all morphisms ,
:
Epimorphisms are categorical analogues of onto or surjective functions (and in the category of sets the concept corresponds exactly to the surjective functions), but they may not exactly coincide in all contexts; for example, the inclusion is a ring epimorphism. The dual
Dual or Duals may refer to:
Paired/two things
* Dual (mathematics), a notion of paired concepts that mirror one another
** Dual (category theory), a formalization of mathematical duality
*** see more cases in :Duality theories
* Dual (grammatical ...
of an epimorphism is a monomorphism (i.e. an epimorphism in a category ''C'' is a monomorphism in the dual category ''C''op).
Many authors in abstract algebra and universal algebra define an epimorphism simply as an ''onto'' or surjective
In mathematics, a surjective function (also known as surjection, or onto function) is a function that every element can be mapped from element so that . In other words, every element of the function's codomain is the image of one element of i ...
homomorphism. Every epimorphism in this algebraic sense is an epimorphism in the sense of category theory, but the converse is not true in all categories. In this article, the term "epimorphism" will be used in the sense of category theory given above. For more on this, see below.
Examples
Every morphism in a concrete category whose underlying function issurjective
In mathematics, a surjective function (also known as surjection, or onto function) is a function that every element can be mapped from element so that . In other words, every element of the function's codomain is the image of one element of i ...
is an epimorphism. In many concrete categories of interest the converse is also true. For example, in the following categories, the epimorphisms are exactly those morphisms that are surjective on the underlying sets:
* Set: sets and functions. To prove that every epimorphism ''f'': ''X'' → ''Y'' in Set is surjective, we compose it with both the characteristic function ''g''1: ''Y'' → of the image ''f''(''X'') and the map ''g''2: ''Y'' → that is constant 1.
*Rel: sets with binary relation
In mathematics, a binary relation associates elements of one set, called the ''domain'', with elements of another set, called the ''codomain''. A binary relation over Set (mathematics), sets and is a new set of ordered pairs consisting of ele ...
s and relation-preserving functions. Here we can use the same proof as for Set, equipping with the full relation ×.
*Pos: partially ordered sets and monotone functions. If ''f'' : (''X'', ≤) → (''Y'', ≤) is not surjective, pick ''y''0 in ''Y'' \ ''f''(''X'') and let ''g''1 : ''Y'' → be the characteristic function of and ''g''2 : ''Y'' → the characteristic function of . These maps are monotone if is given the standard ordering 0 < 1.
* Grp: groups and group homomorphisms. The result that every epimorphism in Grp is surjective is due to Otto Schreier (he actually proved more, showing that every subgroup is an equalizer using the free product with one amalgamated subgroup); an elementary proof can be found in (Linderholm 1970).
*FinGrp: finite groups and group homomorphisms. Also due to Schreier; the proof given in (Linderholm 1970) establishes this case as well.
* Ab: abelian groups and group homomorphisms.
* ''K''-Vect: vector spaces over a field ''K'' and ''K''-linear transformations.
*Mod-''R'': right module
In mathematics, a module is a generalization of the notion of vector space in which the field of scalars is replaced by a ring. The concept of ''module'' generalizes also the notion of abelian group, since the abelian groups are exactly the modu ...
s over a ring ''R'' and module homomorphisms. This generalizes the two previous examples; to prove that every epimorphism ''f'': ''X'' → ''Y'' in Mod-''R'' is surjective, we compose it with both the canonical quotient map ''g'' 1: ''Y'' → ''Y''/''f''(''X'') and the zero map ''g''2: ''Y'' → ''Y''/''f''(''X'').
* Top: topological spaces and continuous function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value ...
s. To prove that every epimorphism in Top is surjective, we proceed exactly as in Set, giving the indiscrete topology, which ensures that all considered maps are continuous.
*HComp: compact Hausdorff spaces and continuous functions. If ''f'': ''X'' → ''Y'' is not surjective, let ''y'' ∈ ''Y'' − ''fX''. Since ''fX'' is closed, by Urysohn's Lemma there is a continuous function ''g''1:''Y'' → ,1such that ''g''1 is 0 on ''fX'' and 1 on ''y''. We compose ''f'' with both ''g''1 and the zero function ''g''2: ''Y'' → ,1
However, there are also many concrete categories of interest where epimorphisms fail to be surjective. A few examples are:
*In the category of monoids
Category, plural categories, may refer to:
Philosophy and general uses
* Categorization, categories in cognitive science, information science and generally
*Category of being
* ''Categories'' (Aristotle)
*Category (Kant)
*Categories (Peirce)
* ...
, Mon, the inclusion map N → Z is a non-surjective epimorphism. To see this, suppose that ''g''1 and ''g''2 are two distinct maps from Z to some monoid ''M''. Then for some ''n'' in Z, ''g''1(''n'') ≠ ''g''2(''n''), so ''g''1(''-n'') ≠ ''g''2(−''n''). Either ''n'' or −''n'' is in N, so the restrictions of ''g''1 and ''g''2 to N are unequal.
*In the category of algebras over commutative ring R, take R ''N→ R ''Z where R ''Gis the group ring of the group G and the morphism is induced by the inclusion N → Z as in the previous example. This follows from the observation that 1 generates the algebra R ''Z(note that the unit in R ''Zis given by 0 of Z), and the inverse of the element represented by n in Z is just the element represented by −n. Thus any homomorphism from R ''Zis uniquely determined by its value on the element represented by 1 of Z.
*In the category of rings, Ring, the inclusion map Z → Q is a non-surjective epimorphism; to see this, note that any ring homomorphism on Q is determined entirely by its action on Z, similar to the previous example. A similar argument shows that the natural ring homomorphism from any commutative ring
In mathematics, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra. Complementarily, noncommutative algebra is the study of ring properties that are not sp ...
''R'' to any one of its localizations is an epimorphism.
*In the category of commutative rings, a finitely generated homomorphism of rings ''f'' : ''R'' → ''S'' is an epimorphism if and only if for all prime ideal
In algebra, a prime ideal is a subset of a ring that shares many important properties of a prime number in the ring of integers. The prime ideals for the integers are the sets that contain all the multiples of a given prime number, together with ...
s ''P'' of ''R'', the ideal ''Q'' generated by ''f''(''P'') is either ''S'' or is prime, and if ''Q'' is not ''S'', the induced map Frac
Frac or FRAC may refer to:
* Frac or fraccing, short name for Hydraulic fracturing, a method for extracting oil and natural gas
* FRAC Act, United States legislation proposed in 2009 to regulate hydraulic fracturing
* Frac module, a format for ...
(''R''/''P'') → Frac(''S''/''Q'') is an isomorphism (EGA
Ega or EGA may refer to:
Military
* East German Army, the common western name for the National People's Army
* Eagle, Globe, and Anchor, the emblem of the United States Marine Corps
People
* Aega (mayor of the palace), 7th-century noble of Neus ...
IV 17.2.6).
*In the category of Hausdorff spaces, Haus, the epimorphisms are precisely the continuous functions with dense images. For example, the inclusion map Q → R, is a non-surjective epimorphism.
The above differs from the case of monomorphisms where it is more frequently true that monomorphisms are precisely those whose underlying functions are injective
In mathematics, an injective function (also known as injection, or one-to-one function) is a function that maps distinct elements of its domain to distinct elements; that is, implies . (Equivalently, implies in the equivalent contrapositiv ...
.
As for examples of epimorphisms in non-concrete categories:
* If a monoid or ring is considered as a category with a single object (composition of morphisms given by multiplication), then the epimorphisms are precisely the right-cancellable elements.
* If a directed graph is considered as a category (objects are the vertices, morphisms are the paths, composition of morphisms is the concatenation of paths), then ''every'' morphism is an epimorphism.
Properties
Every isomorphism is an epimorphism; indeed only a right-sided inverse is needed: if there exists a morphism ''j'' : ''Y'' → ''X'' such that ''fj'' = id''Y'', then ''f'': ''X'' → ''Y'' is easily seen to be an epimorphism. A map with such a right-sided inverse is called a split epi. In a topos, a map that is both amonic morphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from to is often denoted with the notation X\hookrightarrow Y.
In the more general setting of category theory, a monomorphism ...
and an epimorphism is an isomorphism.
The composition of two epimorphisms is again an epimorphism. If the composition ''fg'' of two morphisms is an epimorphism, then ''f'' must be an epimorphism.
As some of the above examples show, the property of being an epimorphism is not determined by the morphism alone, but also by the category of context. If ''D'' is a subcategory
In mathematics, specifically category theory, a subcategory of a category ''C'' is a category ''S'' whose objects are objects in ''C'' and whose morphisms are morphisms in ''C'' with the same identities and composition of morphisms. Intuitivel ...
of ''C'', then every morphism in ''D'' that is an epimorphism when considered as a morphism in ''C'' is also an epimorphism in ''D''. However the converse need not hold; the smaller category can (and often will) have more epimorphisms.
As for most concepts in category theory, epimorphisms are preserved under equivalences of categories: given an equivalence ''F'' : ''C'' → ''D'', a morphism ''f'' is an epimorphism in the category ''C'' if and only if ''F''(''f'') is an epimorphism in ''D''. A duality
Duality may refer to:
Mathematics
* Duality (mathematics), a mathematical concept
** Dual (category theory), a formalization of mathematical duality
** Duality (optimization)
** Duality (order theory), a concept regarding binary relations
** Dual ...
between two categories turns epimorphisms into monomorphisms, and vice versa.
The definition of epimorphism may be reformulated to state that ''f'' : ''X'' → ''Y'' is an epimorphism if and only if the induced maps
:
are injective
In mathematics, an injective function (also known as injection, or one-to-one function) is a function that maps distinct elements of its domain to distinct elements; that is, implies . (Equivalently, implies in the equivalent contrapositiv ...
for every choice of ''Z''. This in turn is equivalent to the induced natural transformation
:
being a monomorphism in the functor category Set''C''.
Every coequalizer is an epimorphism, a consequence of the uniqueness requirement in the definition of coequalizers. It follows in particular that every cokernel is an epimorphism. The converse, namely that every epimorphism be a coequalizer, is not true in all categories.
In many categories it is possible to write every morphism as the composition of an epimorphism followed by a monomorphism. For instance, given a group homomorphism ''f'' : ''G'' → ''H'', we can define the group ''K'' = im(''f'') and then write ''f'' as the composition of the surjective homomorphism ''G'' → ''K'' that is defined like ''f'', followed by the injective homomorphism ''K'' → ''H'' that sends each element to itself. Such a factorization of an arbitrary morphism into an epimorphism followed by a monomorphism can be carried out in all abelian categories and also in all the concrete categories mentioned above in (though not in all concrete categories).
Related concepts
Among other useful concepts are ''regular epimorphism'', ''extremal epimorphism'', ''immediate epimorphism'', ''strong epimorphism'', and ''split epimorphism''. * An epimorphism is said to be regular if it is a coequalizer of some pair of parallel morphisms. * An epimorphism is said to be extremal if in each representation , where is a monomorphism, the morphism is automatically an isomorphism. * An epimorphism is said to be immediate if in each representation , where is a monomorphism and is an epimorphism, the morphism is automatically an isomorphism. * An epimorphism is said to be strong if for any monomorphism and any morphisms and such that , there exists a morphism such that and .
* An epimorphism is said to be split if there exists a morphism such that (in this case is called a right-sided inverse for ).
There is also the notion of homological epimorphism in ring theory. A morphism ''f'': ''A'' → ''B'' of rings is a homological epimorphism if it is an epimorphism and it induces a full and faithful functor on derived categories:
D(''f'') : D(''B'') → D(''A'').
A morphism that is both a monomorphism and an epimorphism is called a bimorphism. Every isomorphism is a bimorphism but the converse is not true in general. For example, the map from the half-open interval ,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane">unit circle">,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane) that sends ''x'' to exp(2πi''x'') (see Euler's formula) is continuous and bijective but not a homeomorphism since the inverse map is not continuous at 1, so it is an instance of a bimorphism that is not an isomorphism in the category Top. Another example is the embedding Q → R in the category Haus; as noted above, it is a bimorphism, but it is not bijective and therefore not an isomorphism. Similarly, in the category of rings, the map Z → Q is a bimorphism but not an isomorphism.
Epimorphisms are used to define abstract
An epimorphism is said to be strong if for any monomorphism and any morphisms and such that , there exists a morphism such that and .
* An epimorphism is said to be split if there exists a morphism such that (in this case is called a right-sided inverse for ).
There is also the notion of homological epimorphism in ring theory. A morphism ''f'': ''A'' → ''B'' of rings is a homological epimorphism if it is an epimorphism and it induces a full and faithful functor on derived categories:
D(''f'') : D(''B'') → D(''A'').
A morphism that is both a monomorphism and an epimorphism is called a bimorphism. Every isomorphism is a bimorphism but the converse is not true in general. For example, the map from the half-open interval ,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane">unit circle">,1) to the unit circle S1 (thought of as a topological subspace">subspace of the complex plane) that sends ''x'' to exp(2πi''x'') (see Euler's formula) is continuous and bijective but not a homeomorphism since the inverse map is not continuous at 1, so it is an instance of a bimorphism that is not an isomorphism in the category Top. Another example is the embedding Q → R in the category Haus; as noted above, it is a bimorphism, but it is not bijective and therefore not an isomorphism. Similarly, in the category of rings, the map Z → Q is a bimorphism but not an isomorphism.
Epimorphisms are used to define abstract quotient object In category theory, a branch of mathematics, a subobject is, roughly speaking, an object that sits inside another object in the same category. The notion is a generalization of concepts such as subsets from set theory, subgroups from group theory,M ...
s in general categories: two epimorphisms ''f''1 : ''X'' → ''Y''1 and ''f''2 : ''X'' → ''Y''2 are said to be ''equivalent'' if there exists an isomorphism ''j'' : ''Y''1 → ''Y''2 with ''j'' ''f''1 = ''f''2. This is an equivalence relation
In mathematics, an equivalence relation is a binary relation that is reflexive, symmetric and transitive. The equipollence relation between line segments in geometry is a common example of an equivalence relation.
Each equivalence relation ...
, and the equivalence classes are defined to be the quotient objects of ''X''.
Terminology
The companion terms ''epimorphism'' and '' monomorphism'' were first introduced by Bourbaki. Bourbaki uses ''epimorphism'' as shorthand for a surjective function. Early category theorists believed that epimorphisms were the correct analogue of surjections in an arbitrary category, similar to how monomorphisms are very nearly an exact analogue of injections. Unfortunately this is incorrect; strong or regular epimorphisms behave much more closely to surjections than ordinary epimorphisms. Saunders Mac Lane attempted to create a distinction between ''epimorphisms'', which were maps in a concrete category whose underlying set maps were surjective, and ''epic morphisms'', which are epimorphisms in the modern sense. However, this distinction never caught on. It is a common mistake to believe that epimorphisms are either identical to surjections or that they are a better concept. Unfortunately this is rarely the case; epimorphisms can be very mysterious and have unexpected behavior. It is very difficult, for example, to classify all the epimorphisms of rings. In general, epimorphisms are their own unique concept, related to surjections but fundamentally different.See also
* List of category theory topics * MonomorphismNotes
References
* * * * * * *External links
* *{{nlab, id=strong+epimorphism, title=Strong epimorphism Morphisms Algebraic properties of elements