dipolar on:
[Wikipedia]
[Google]
[Amazon]
 In
In  A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles—not to be confused with monopoles, see Classification below)—and may be labeled "north" and "south". In terms of the Earth's magnetic field, they are respectively "north-seeking" and "south-seeking" poles: if the magnet were freely suspended in the Earth's magnetic field, the north-seeking pole would point towards the north and the south-seeking pole would point towards the south. The dipole moment of the bar magnet points from its magnetic south to its magnetic
A permanent magnet, such as a bar magnet, owes its magnetism to the intrinsic magnetic dipole moment of the electron. The two ends of a bar magnet are referred to as poles—not to be confused with monopoles, see Classification below)—and may be labeled "north" and "south". In terms of the Earth's magnetic field, they are respectively "north-seeking" and "south-seeking" poles: if the magnet were freely suspended in the Earth's magnetic field, the north-seeking pole would point towards the north and the south-seeking pole would point towards the south. The dipole moment of the bar magnet points from its magnetic south to its magnetic


 A ''physical dipole'' consists of two equal and opposite point charges: in the literal sense, two poles. Its field at large distances (i.e., distances large in comparison to the separation of the poles) depends almost entirely on the dipole moment as defined above. A ''point (electric) dipole'' is the limit obtained by letting the separation tend to 0 while keeping the dipole moment fixed. The field of a point dipole has a particularly simple form, and the order-1 term in the multipole expansion is precisely the point dipole field.
Although there are no known
A ''physical dipole'' consists of two equal and opposite point charges: in the literal sense, two poles. Its field at large distances (i.e., distances large in comparison to the separation of the poles) depends almost entirely on the dipole moment as defined above. A ''point (electric) dipole'' is the limit obtained by letting the separation tend to 0 while keeping the dipole moment fixed. The field of a point dipole has a particularly simple form, and the order-1 term in the multipole expansion is precisely the point dipole field.
Although there are no known
 Potassium bromide (KBr) has one of the highest dipole moments because it is an ionic compound that exists as a molecule in the gas phase.
Potassium bromide (KBr) has one of the highest dipole moments because it is an ionic compound that exists as a molecule in the gas phase.
 The overall dipole moment of a molecule may be approximated as a
The overall dipole moment of a molecule may be approximated as a 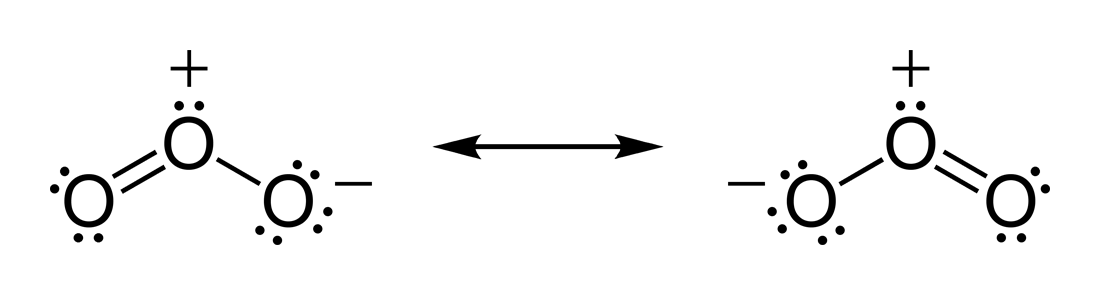 An example in organic chemistry of the role of geometry in determining dipole moment is the ''cis'' and ''trans'' isomers of
An example in organic chemistry of the role of geometry in determining dipole moment is the ''cis'' and ''trans'' isomers of
 In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time. It is an extension, or a more physical next-step, to
In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time. It is an extension, or a more physical next-step, to
USGS Geomagnetism Program
a chapter from an online textbook
Electric Dipole Potential
by
Energy Density of a Magnetic Dipole
by Franz Krafft.
physics
Physics is the natural science that studies matter, its fundamental constituents, its motion and behavior through space and time, and the related entities of energy and force. "Physical science is that department of knowledge which r ...
, a dipole () is an electromagnetic
In physics, electromagnetism is an interaction that occurs between particles with electric charge. It is the second-strongest of the four fundamental interactions, after the strong force, and it is the dominant force in the interactions o ...
phenomenon which occurs in two ways:
*An electric dipole
The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb- meter (C⋅m). T ...
deals with the separation of the positive and negative electric charge
Electric charge is the physical property of matter that causes charged matter to experience a force when placed in an electromagnetic field. Electric charge can be ''positive'' or ''negative'' (commonly carried by protons and electrons respe ...
s found in any electromagnetic system. A simple example of this system is a pair of charges of equal magnitude but opposite sign separated by some typically small distance. (A permanent electric dipole is called an electret
An electret (formed as a portmanteau of ''electr-'' from "electricity" and ''-et'' from "magnet") is a dielectric material that has a quasi-permanent electric charge or dipole polarization (electrostatics), polarisation. An electret generates int ...
.)
*A magnetic dipole
In electromagnetism, a magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the size of the source is reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric ...
is the closed circulation of an electric current system. A simple example is a single loop of wire with constant current through it. A bar magnet
A magnet is a material or object that produces a magnetic field. This magnetic field is invisible but is responsible for the most notable property of a magnet: a force that pulls on other ferromagnetic materials, such as iron, steel, nicke ...
is an example of a magnet with a permanent magnetic dipole moment.
Dipoles, whether electric or magnetic, can be characterized by their dipole moment, a vector quantity. For the simple electric dipole, the electric dipole moment points from the negative charge towards the positive charge, and has a magnitude equal to the strength of each charge times the separation between the charges. (To be precise: for the definition of the dipole moment, one should always consider the "dipole limit", where, for example, the distance of the generating charges should ''converge'' to 0 while simultaneously, the charge strength should ''diverge'' to infinity in such a way that the product remains a positive constant.)
For the magnetic (dipole) current loop, the magnetic dipole moment points through the loop (according to the right hand grip rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding orientation of axes in three-dimensional space. It is also a convenient method for quickly finding the direction of a cross-product of 2 vectors.
Most of t ...
), with a magnitude equal to the current in the loop times the area of the loop.
Similar to magnetic current loops, the electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
particle and some other fundamental particle
In particle physics, an elementary particle or fundamental particle is a subatomic particle that is not composed of other particles. Particles currently thought to be elementary include electrons, the fundamental fermions (quarks, leptons, antiqu ...
s have magnetic dipole moments, as an electron generates a magnetic field identical to that generated by a very small current loop. However, an electron's magnetic dipole moment is not due to a current loop, but to an intrinsic
In science and engineering, an intrinsic property is a property of a specified subject that exists itself or within the subject. An extrinsic property is not essential or inherent to the subject that is being characterized. For example, mass ...
property of the electron. The electron may also have an ''electric'' dipole moment though such has yet to be observed (see electron electric dipole moment
The electron electric dipole moment is an intrinsic property of an electron such that the potential energy is linearly related to the strength of the electric field:
:U = \mathbf d_ \cdot \mathbf E.
The electron's electric dipole moment (EDM) m ...
).
north pole
The North Pole, also known as the Geographic North Pole or Terrestrial North Pole, is the point in the Northern Hemisphere where the Earth's rotation, Earth's axis of rotation meets its surface. It is called the True North Pole to distingu ...
. In a magnetic compass
A compass is a device that shows the cardinal directions used for navigation and geographic orientation. It commonly consists of a magnetized needle or other element, such as a compass card or compass rose, which can pivot to align itself wit ...
, the north pole of a bar magnet points north. However, that means that Earth's geomagnetic north pole is the ''south'' pole (south-seeking pole) of its dipole moment and vice versa.
The only known mechanisms for the creation of magnetic dipoles are by current loops or quantum-mechanical spin since the existence of magnetic monopole
In particle physics, a magnetic monopole is a hypothetical elementary particle that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice versa). A magnetic monopole would have a net north or south "magneti ...
s has never been experimentally demonstrated.
Classification
magnetic monopole
In particle physics, a magnetic monopole is a hypothetical elementary particle that is an isolated magnet with only one magnetic pole (a north pole without a south pole or vice versa). A magnetic monopole would have a net north or south "magneti ...
s in nature, there are magnetic dipoles in the form of the quantum-mechanical spin associated with particles such as electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
s (although the accurate description of such effects falls outside of classical electromagnetism). A theoretical magnetic ''point dipole'' has a magnetic field of exactly the same form as the electric field of an electric point dipole. A very small current-carrying loop is approximately a magnetic point dipole; the magnetic dipole moment of such a loop is the product of the current flowing in the loop and the (vector) area of the loop.
Any configuration of charges or currents has a 'dipole moment', which describes the dipole whose field is the best approximation, at large distances, to that of the given configuration. This is simply one term in the multipole expansion when the total charge ("monopole moment") is 0—as it ''always'' is for the magnetic case, since there are no magnetic monopoles. The dipole term is the dominant one at large distances: Its field falls off in proportion to , as compared to for the next (quadrupole
A quadrupole or quadrapole is one of a sequence of configurations of things like electric charge or current, or gravitational mass that can exist in ideal form, but it is usually just part of a multipole expansion of a more complex structure refl ...
) term and higher powers of for higher terms, or for the monopole term.
Molecular dipoles
Manymolecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
s have such dipole moments due to non-uniform distributions of positive and negative charges on the various atoms. Such is the case with polar compounds like hydrogen fluoride (HF), where electron density
In quantum chemistry, electron density or electronic density is the measure of the probability of an electron being present at an infinitesimal element of space surrounding any given point. It is a scalar quantity depending upon three spatial va ...
is shared unequally between atoms. Therefore, a molecule's dipole is an electric dipole
The electric dipole moment is a measure of the separation of positive and negative electrical charges within a system, that is, a measure of the system's overall polarity. The SI unit for electric dipole moment is the coulomb- meter (C⋅m). T ...
with an inherent electric field that should not be confused with a magnetic dipole
In electromagnetism, a magnetic dipole is the limit of either a closed loop of electric current or a pair of poles as the size of the source is reduced to zero while keeping the magnetic moment constant. It is a magnetic analogue of the electric ...
, which generates a magnetic field.
The physical chemist Peter J. W. Debye was the first scientist to study molecular dipoles extensively, and, as a consequence, dipole moments are measured in the non- SI unit named ''debye
The debye (symbol: D) (; ) is a CGS unit (a non- SI metric unit) of electric dipole momentTwo equal and opposite charges separated by some distance constitute an electric dipole. This dipole possesses an electric dipole moment whose value is g ...
'' in his honor.
For molecules there are three types of dipoles:
; Permanent dipoles: These occur when two atoms in a molecule have substantially different electronegativity
Electronegativity, symbolized as , is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the ...
: One atom attracts electrons more than another, becoming more negative, while the other atom becomes more positive. A molecule with a permanent dipole moment is called a ''polar'' molecule. See dipole–dipole attractions.
; Instantaneous dipoles:These occur due to chance when electron
The electron ( or ) is a subatomic particle with a negative one elementary electric charge. Electrons belong to the first generation of the lepton particle family,
and are generally thought to be elementary particles because they have no ...
s happen to be more concentrated in one place than another in a molecule
A molecule is a group of two or more atoms held together by attractive forces known as chemical bonds; depending on context, the term may or may not include ions which satisfy this criterion. In quantum physics, organic chemistry, and bioche ...
, creating a temporary dipole. These dipoles are smaller in magnitude than permanent dipoles, but still play a large role in chemistry and biochemistry due to their prevalence. See instantaneous dipole.
; Induced dipoles: These can occur when one molecule with a permanent dipole repels another molecule's electrons, ''inducing'' a dipole moment in that molecule. A molecule is ''polarized'' when it carries an induced dipole. See induced-dipole attraction.
More generally, an induced dipole of ''any'' polarizable charge distribution ''ρ'' (remember that a molecule has a charge distribution) is caused by an electric field external to ''ρ''. This field may, for instance, originate from an ion or polar molecule in the vicinity of ''ρ'' or may be macroscopic (e.g., a molecule between the plates of a charged capacitor
A capacitor is a device that stores electrical energy in an electric field by virtue of accumulating electric charges on two close surfaces insulated from each other. It is a passive electronic component with two terminals.
The effect of ...
). The size of the induced dipole moment is equal to the product of the strength of the external field and the dipole polarizability
Polarizability usually refers to the tendency of matter, when subjected to an electric field, to acquire an electric dipole moment in proportion to that applied field. It is a property of all matter, considering that matter is made up of elementar ...
of ''ρ''.
Dipole moment values can be obtained from measurement of the dielectric constant. Some typical gas phase values in debye
The debye (symbol: D) (; ) is a CGS unit (a non- SI metric unit) of electric dipole momentTwo equal and opposite charges separated by some distance constitute an electric dipole. This dipole possesses an electric dipole moment whose value is g ...
units are:
* carbon dioxide
Carbon dioxide ( chemical formula ) is a chemical compound made up of molecules that each have one carbon atom covalently double bonded to two oxygen atoms. It is found in the gas state at room temperature. In the air, carbon dioxide is trans ...
: 0
* carbon monoxide
Carbon monoxide (chemical formula CO) is a colorless, poisonous, odorless, tasteless, flammable gas that is slightly less dense than air. Carbon monoxide consists of one carbon atom and one oxygen atom connected by a triple bond. It is the simple ...
: 0.112 D
* ozone
Ozone (), or trioxygen, is an inorganic molecule with the chemical formula . It is a pale blue gas with a distinctively pungent smell. It is an allotrope of oxygen that is much less stable than the diatomic allotrope , breaking down in the lo ...
: 0.53 D
* phosgene: 1.17 D
* NH3 has a dipole moment of 1.42 D
* water vapor
(99.9839 °C)
, -
, Boiling point
,
, -
, specific gas constant
, 461.5 J/( kg·K)
, -
, Heat of vaporization
, 2.27 MJ/kg
, -
, Heat capacity
, 1.864 kJ/(kg·K)
Water vapor, water vapour or aqueous vapor is the gaseous p ...
: 1.85 D
* hydrogen cyanide: 2.98 D
* cyanamide
Cyanamide is an organic compound with the formula C N2 H2. This white solid is widely used in agriculture and the production of pharmaceuticals and other organic compounds. It is also used as an alcohol-deterrent drug. The molecule features a ...
: 4.27 D
* potassium bromide: 10.41 D
vector sum
In mathematics, physics, and engineering, a Euclidean vector or simply a vector (sometimes called a geometric vector or spatial vector) is a geometric object that has magnitude (or length) and direction. Vectors can be added to other vectors a ...
of bond dipole moment
In chemistry, polarity is a separation of electric charge leading to a molecule or its chemical groups having an electric dipole moment, with a negatively charged end and a positively charged end.
Polar molecules must contain one or more polar ...
s. As a vector sum it depends on the relative orientation of the bonds, so that from the dipole moment information can be deduced about the molecular geometry
Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that dete ...
.
For example, the zero dipole of CO2 implies that the two C=O bond dipole moments cancel so that the molecule must be linear. For H2O the O−H bond moments do not cancel because the molecule is bent. For ozone (O3) which is also a bent molecule, the bond dipole moments are not zero even though the O−O bonds are between similar atoms. This agrees with the Lewis structures for the resonance forms of ozone which show a positive charge on the central oxygen atom.
 An example in organic chemistry of the role of geometry in determining dipole moment is the ''cis'' and ''trans'' isomers of
An example in organic chemistry of the role of geometry in determining dipole moment is the ''cis'' and ''trans'' isomers of 1,2-dichloroethene
1,2-Dichloroethene, commonly called 1,2-dichloroethylene or 1,2-DCE, is the name for a pair of organochlorine compounds with the molecular formula CHCl. They are both colorless liquids with a sweet odor. It can exist as either of two geometric ...
. In the ''cis'' isomer the two polar C−Cl bonds are on the same side of the C=C double bond and the molecular dipole moment is 1.90 D. In the ''trans'' isomer, the dipole moment is zero because the two C−Cl bonds are on opposite sides of the C=C and cancel (and the two bond moments for the much less polar C−H bonds also cancel).
Another example of the role of molecular geometry is boron trifluoride, which has three polar bonds with a difference in electronegativity
Electronegativity, symbolized as , is the tendency for an atom of a given chemical element to attract shared electrons (or electron density) when forming a chemical bond. An atom's electronegativity is affected by both its atomic number and the ...
greater than the traditionally cited threshold of 1.7 for ionic bonding
Ionic bonding is a type of chemical bonding that involves the electrostatic attraction between oppositely charged ions, or between two atoms with sharply different electronegativities, and is the primary interaction occurring in ionic compounds ...
. However, due to the equilateral triangular distribution of the fluoride ions centered on and in the same plane as the boron cation, the symmetry of the molecule results in its dipole moment being zero.
Quantum mechanical dipole operator
Consider a collection of ''N'' particles with charges ''qi'' and position vectors r''i''. For instance, this collection may be a molecule consisting of electrons, all withcharge
Charge or charged may refer to:
Arts, entertainment, and media Films
* '' Charge, Zero Emissions/Maximum Speed'', a 2011 documentary
Music
* ''Charge'' (David Ford album)
* ''Charge'' (Machel Montano album)
* ''Charge!!'', an album by The Aqu ...
−''e'', and nuclei with charge ''eZi'', where ''Zi'' is the atomic number
The atomic number or nuclear charge number (symbol ''Z'') of a chemical element is the charge number of an atomic nucleus. For ordinary nuclei, this is equal to the proton number (''n''p) or the number of protons found in the nucleus of every ...
of the ''i'' th nucleus.
The dipole observable (physical quantity) has the quantum mechanical dipole operator:
:
Notice that this definition is valid only for neutral atoms or molecules, i.e. total charge equal to zero. In the ionized case, we have
:
where is the center of mass of the molecule/group of particles.
Atomic dipoles
A non-degenerate (''S''-state) atom can have only a zero permanent dipole. This fact follows quantum mechanically from the inversion symmetry of atoms. All 3 components of the dipole operator are antisymmetric underinversion
Inversion or inversions may refer to:
Arts
* , a French gay magazine (1924/1925)
* ''Inversion'' (artwork), a 2005 temporary sculpture in Houston, Texas
* Inversion (music), a term with various meanings in music theory and musical set theory
* ...
with respect to the nucleus,
:
where is the dipole operator and is the inversion operator.
The permanent dipole moment of an atom in a non-degenerate state (see degenerate energy level
Degeneracy, degenerate, or degeneration may refer to:
Arts and entertainment
* ''Degenerate'' (album), a 2010 album by the British band Trigger the Bloodshed
* Degenerate art, a term adopted in the 1920s by the Nazi Party in Germany to descr ...
) is given as the expectation (average) value of the dipole operator,
:
where is an ''S''-state, non-degenerate, wavefunction, which is symmetric or antisymmetric under inversion: . Since the product of the wavefunction (in the ket) and its complex conjugate (in the bra) is always symmetric under inversion and its inverse,
:
it follows that the expectation value changes sign under inversion. We used here the fact that , being a symmetry operator, is unitary
Unitary may refer to:
Mathematics
* Unitary divisor
* Unitary element
* Unitary group
* Unitary matrix
* Unitary morphism
* Unitary operator
* Unitary transformation
* Unitary representation
* Unitarity (physics)
* ''E''-unitary inverse semigrou ...
: and by definition the Hermitian adjoint may be moved from bra to ket and then becomes . Since the only quantity that is equal to minus itself is the zero, the expectation value vanishes,
:
In the case of open-shell atoms with degenerate energy levels, one could define a dipole moment by the aid of the first-order Stark effect. This gives a non-vanishing dipole (by definition proportional to a non-vanishing first-order Stark shift) only if some of the wavefunctions belonging to the degenerate energies have opposite parity; i.e., have different behavior under inversion. This is a rare occurrence, but happens for the excited H-atom, where 2s and 2p states are "accidentally" degenerate (see article Laplace–Runge–Lenz vector
In classical mechanics, the Laplace–Runge–Lenz (LRL) vector is a vector used chiefly to describe the shape and orientation of the orbit of one astronomical body around another, such as a binary star or a planet revolving around a star. For t ...
for the origin of this degeneracy) and have opposite parity (2s is even and 2p is odd).
Field of a static magnetic dipole
Magnitude
The far-field strength, ''B'', of a dipole magnetic field is given by : where :''B'' is the strength of the field, measured in teslas :''r'' is the distance from the center, measured in metres :''λ'' is the magnetic latitude (equal to 90° − ''θ'') where ''θ'' is the magnetic colatitude, measured inradian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before tha ...
s or degrees from the dipole axisMagnetic colatitude is 0 along the dipole's axis and 90° in the plane perpendicular to its axis.
:''m'' is the dipole moment, measured in ampere-square metres or joule
The joule ( , ; symbol: J) is the unit of energy in the International System of Units (SI). It is equal to the amount of work done when a force of 1 newton displaces a mass through a distance of 1 metre in the direction of the force applie ...
s per tesla
:''μ''0 is the permeability of free space
The vacuum magnetic permeability (variously ''vacuum permeability'', ''permeability of free space'', ''permeability of vacuum''), also known as the magnetic constant, is the magnetic permeability in a classical vacuum. It is a physical constan ...
, measured in henries
The henry (symbol: H) is the unit of electrical inductance in the International System of Units (SI). If a current of 1 ampere flowing through a coil produces flux linkage of 1 weber turn, that coil has a self inductance of 1 henry. The un ...
per metre.
Conversion to cylindrical coordinates is achieved using and
:
where ''ρ'' is the perpendicular distance from the ''z''-axis. Then,
:
Vector form
The field itself is a vector quantity: : where :B is the field :r is the vector from the position of the dipole to the position where the field is being measured :''r'' is the absolute value of r: the distance from the dipole :r̂ = is the unit vector parallel to r; :m is the (vector) dipole moment :''μ''0 is the permeability of free space : This is ''exactly'' the field of a point dipole, ''exactly'' the dipole term in the multipole expansion of an arbitrary field, and ''approximately'' the field of any dipole-like configuration at large distances.Magnetic vector potential
Thevector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a ''scalar potential'', which is a scalar field whose gradient is a given vector field.
Formally, given a vector field v, a ''vecto ...
A of a magnetic dipole is
:
with the same definitions as above.
Field from an electric dipole
Theelectrostatic potential
Electrostatics is a branch of physics that studies electric charges at rest ( static electricity).
Since classical times, it has been known that some materials, such as amber, attract lightweight particles after rubbing. The Greek word for ambe ...
at position r due to an electric dipole at the origin is given by:
:
where p is the (vector) dipole moment, and ''є''0 is the permittivity of free space.
This term appears as the second term in the multipole expansion of an arbitrary electrostatic potential Φ(r). If the source of Φ(r) is a dipole, as it is assumed here, this term is the only non-vanishing term in the multipole expansion of Φ(r). The electric field from a dipole can be found from the gradient
In vector calculus, the gradient of a scalar-valued differentiable function of several variables is the vector field (or vector-valued function) \nabla f whose value at a point p is the "direction and rate of fastest increase". If the gr ...
of this potential:
:
This is of the same form of the expression for the magnetic field of a point magnetic dipole, ignoring the delta function.
In a real electric dipole, however, the charges are physically separate and the electric field diverges or converges at the point charges.
This is different to the magnetic field of a real magnetic dipole which is continuous everywhere. The delta function represents the strong field pointing in the opposite direction between the point charges, which is often omitted since one is rarely interested in the field at the dipole's position.
For further discussions about the internal field of dipoles, see or Magnetic moment#Internal magnetic field of a dipole.
Torque on a dipole
Since the direction of an electric field is defined as the direction of the force on a positive charge, electric field lines point away from a positive charge and toward a negative charge. When placed in a homogeneouselectric
Electricity is the set of physical phenomena associated with the presence and motion of matter that has a property of electric charge. Electricity is related to magnetism, both being part of the phenomenon of electromagnetism, as described by ...
or magnetic field, equal but opposite forces arise on each side of the dipole creating a torque
In physics and mechanics, torque is the rotational equivalent of linear force. It is also referred to as the moment of force (also abbreviated to moment). It represents the capability of a force to produce change in the rotational motion of th ...
}:
:
for an electric dipole moment p (in coulomb-meters), or
:
for a magnetic dipole moment m (in ampere-square meters).
The resulting torque will tend to align the dipole with the applied field, which in the case of an electric dipole, yields a potential energy of
:.
The energy of a magnetic dipole is similarly
:.
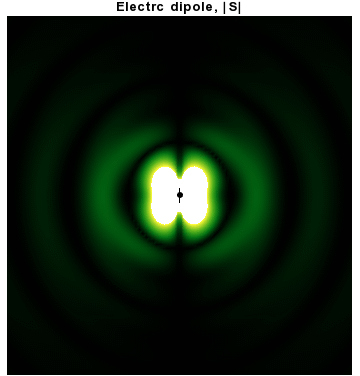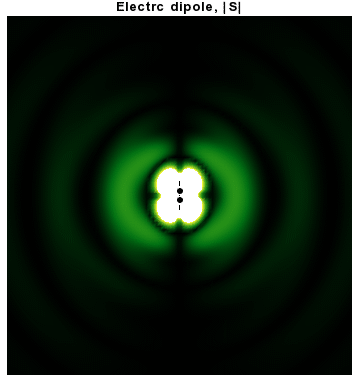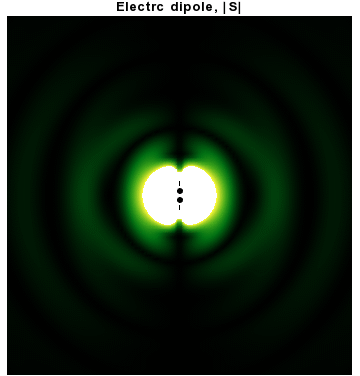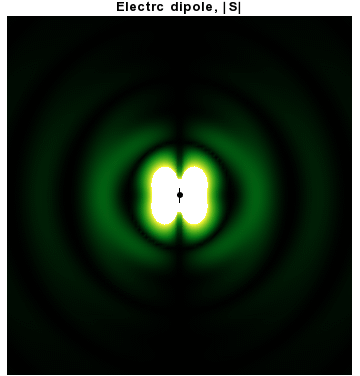
Dipole radiation
 In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time. It is an extension, or a more physical next-step, to
In addition to dipoles in electrostatics, it is also common to consider an electric or magnetic dipole that is oscillating in time. It is an extension, or a more physical next-step, to spherical wave
The (two-way) wave equation is a second-order linear partial differential equation for the description of waves or standing wave fields — as they occur in classical physics — such as mechanical waves (e.g. water waves, sound waves and seis ...
radiation.
In particular, consider a harmonically oscillating electric dipole, with angular frequency
In physics, angular frequency "''ω''" (also referred to by the terms angular speed, circular frequency, orbital frequency, radian frequency, and pulsatance) is a scalar measure of rotation rate. It refers to the angular displacement per unit tim ...
''ω'' and a dipole moment ''p''0 along the ẑ direction of the form
:
In vacuum, the exact field produced by this oscillating dipole can be derived using the retarded potential
In electrodynamics, the retarded potentials are the electromagnetic potentials for the electromagnetic field generated by time-varying electric current or charge distributions in the past. The fields propagate at the speed of light ''c'', so th ...
formulation as:
:
For ≫ 1, the far-field takes the simpler form of a radiating "spherical" wave, but with angular dependence embedded in the cross-product: David J. Griffiths, Introduction to Electrodynamics, Prentice Hall, 1999, page 447
:
The time-averaged Poynting vector
:
is not distributed isotropically, but concentrated around the directions lying perpendicular to the dipole moment, as a result of the non-spherical electric and magnetic waves. In fact, the spherical harmonic
In mathematics and physical science, spherical harmonics are special functions defined on the surface of a sphere. They are often employed in solving partial differential equations in many scientific fields.
Since the spherical harmonics form ...
function (sin ''θ'') responsible for such toroidal angular distribution is precisely the ''l'' = 1 "p" wave.
The total time-average power radiated by the field can then be derived from the Poynting vector as
:
Notice that the dependence of the power on the fourth power of the frequency of the radiation is in accordance with the Rayleigh scattering
Rayleigh scattering ( ), named after the 19th-century British physicist Lord Rayleigh (John William Strutt), is the predominantly elastic scattering of light or other electromagnetic radiation by particles much smaller than the wavelength of th ...
, and the underlying effects why the sky consists of mainly blue colour.
A circular polarized dipole is described as a superposition of two linear dipoles.
See also
*Polarization density
In classical electromagnetism, polarization density (or electric polarization, or simply polarization) is the vector field that expresses the density of permanent or induced electric dipole moments in a dielectric material. When a dielectric is ...
* Magnetic dipole models
* Dipole model of the Earth's magnetic field
The dipole model of the Earth's magnetic field is a first order approximation of the rather complex true Earth's magnetic field. Due to effects of the interplanetary magnetic field (IMF), and the solar wind, the dipole model is particularly ina ...
* Electret
An electret (formed as a portmanteau of ''electr-'' from "electricity" and ''-et'' from "magnet") is a dielectric material that has a quasi-permanent electric charge or dipole polarization (electrostatics), polarisation. An electret generates int ...
* Indian Ocean Dipole
The Indian Ocean Dipole (IOD), also known as the Indian Niño, is an irregular oscillation of sea surface temperatures in which the western Indian Ocean becomes alternately warmer (positive phase) and then colder (negative phase) than the eastern ...
and Subtropical Indian Ocean Dipole, two oceanographic phenomena
* Magnetic dipole-dipole interaction
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particle ...
* Spin magnetic moment
In physics, mainly quantum mechanics and particle physics, a spin magnetic moment is the magnetic moment caused by the spin of elementary particles. For example, the electron is an elementary spin-1/2 fermion. Quantum electrodynamics gives the ...
* Monopole
* Solid harmonics In physics and mathematics, the solid harmonics are solutions of the Laplace equation in spherical polar coordinates, assumed to be (smooth) functions \mathbb^3 \to \mathbb. There are two kinds: the ''regular solid harmonics'' R^m_\ell(\mathbf), wh ...
* Axial multipole moments
Axial multipole moments are a series expansion of the electric potential of a charge distribution localized close to the origin along one Cartesian axis, denoted here as the ''z''-axis. However, the axial multipole expansion can also be applied ...
* Cylindrical multipole moments
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R. Such potentials arise in the electric potential of long line charges, and the anal ...
* Spherical multipole moments
Spherical multipole moments are the coefficients in a series expansion
of a potential that varies inversely with the distance R to a source, ''i.e.'', as 1/''R''. Examples of such potentials are the electric potential, the magnetic potential ...
* Laplace expansion
In linear algebra, the Laplace expansion, named after Pierre-Simon Laplace, also called cofactor expansion, is an expression of the determinant of an matrix as a weighted sum of minors, which are the determinants of some submatrices of . Spec ...
* Molecular solid
A molecular solid is a solid consisting of discrete molecules. The cohesive forces that bind the molecules together are van der Waals forces, dipole-dipole interactions, quadrupole interactions, π-π interactions, hydrogen bonding, halogen b ...
* Magnetic moment#Internal magnetic field of a dipole
Notes
References
{{ReflistExternal links
USGS Geomagnetism Program
a chapter from an online textbook
Electric Dipole Potential
by
Stephen Wolfram
Stephen Wolfram (; born 29 August 1959) is a British-American computer scientist, physicist, and businessman. He is known for his work in computer science, mathematics, and theoretical physics. In 2012, he was named a fellow of the American Ma ...
anEnergy Density of a Magnetic Dipole
by Franz Krafft.
Wolfram Demonstrations Project
The Wolfram Demonstrations Project is an organized, open-source collection of small (or medium-size) interactive programs called Demonstrations, which are meant to visually and interactively represent ideas from a range of fields. It is hos ...
.
Electromagnetism
Potential theory