Cylindrical Multipole Moments
Cylindrical multipole moments are the coefficients in a series expansion of a potential that varies logarithmically with the distance to a source, i.e., as \ln \ R. Such potentials arise in the electric potential of long line charges, and the analogous sources for the magnetic potential and gravitational potential. For clarity, we illustrate the expansion for a single line charge, then generalize to an arbitrary distribution of line charges. Through this article, the primed coordinates such as (\rho^, \theta^) refer to the position of the line charge(s), whereas the unprimed coordinates such as (\rho, \theta) refer to the point at which the potential is being observed. We use cylindrical coordinates throughout, e.g., an arbitrary vector \mathbf has coordinates ( \rho, \theta, z) where \rho is the radius from the z axis, \theta is the azimuthal angle and z is the normal Cartesian coordinate. By assumption, the line charges are infinitely long and aligned with the z axis. Cylind ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]  

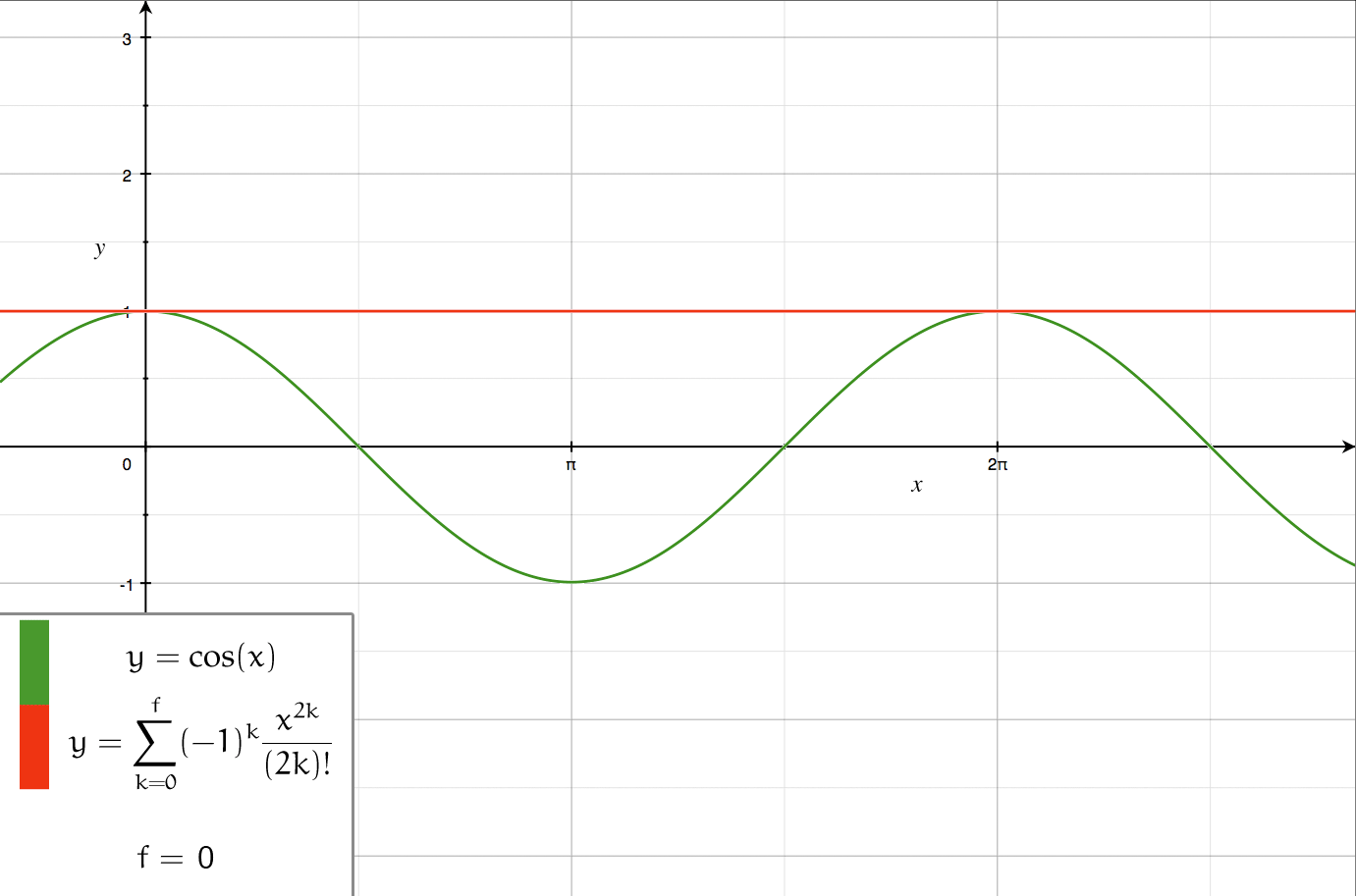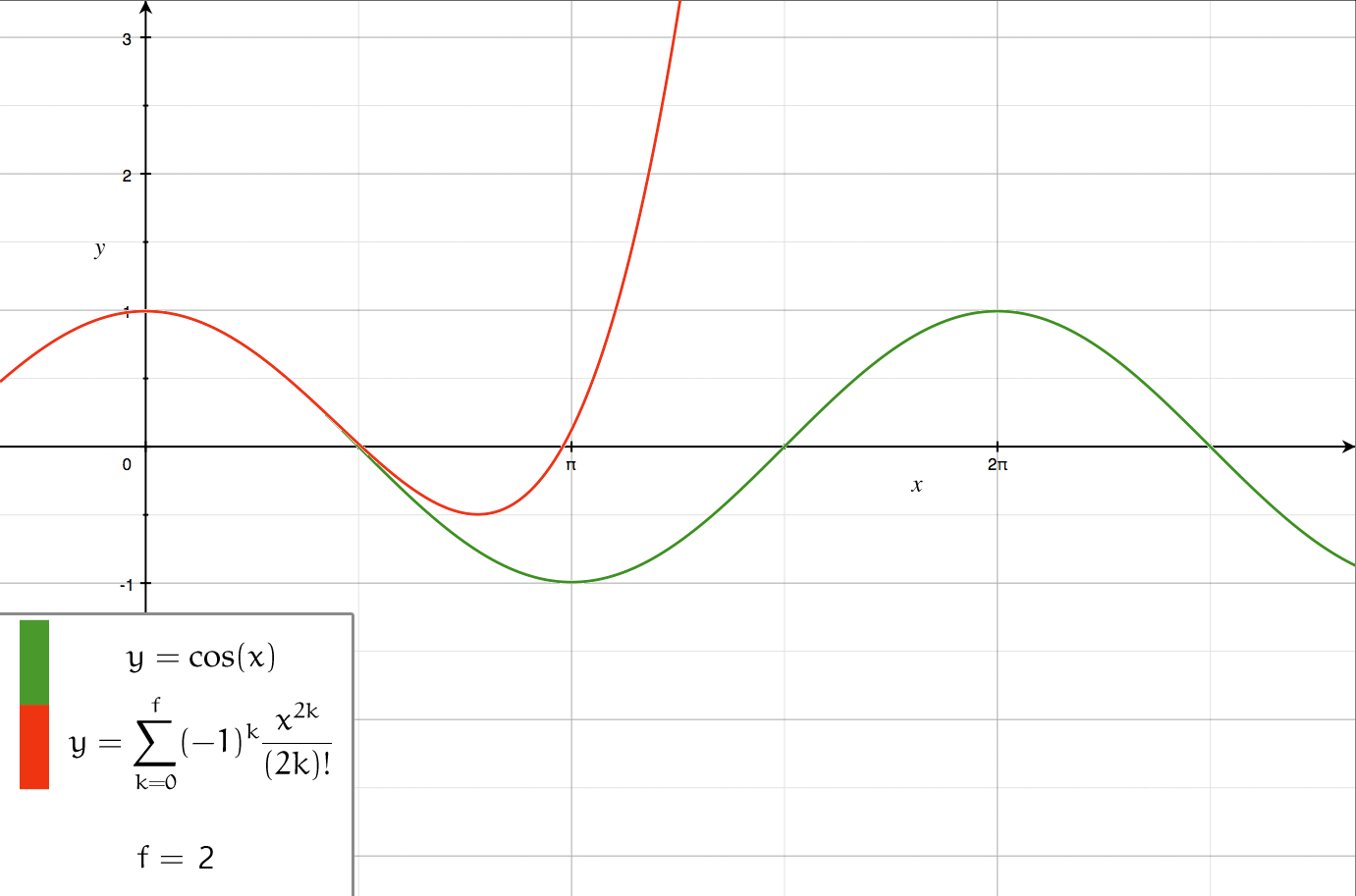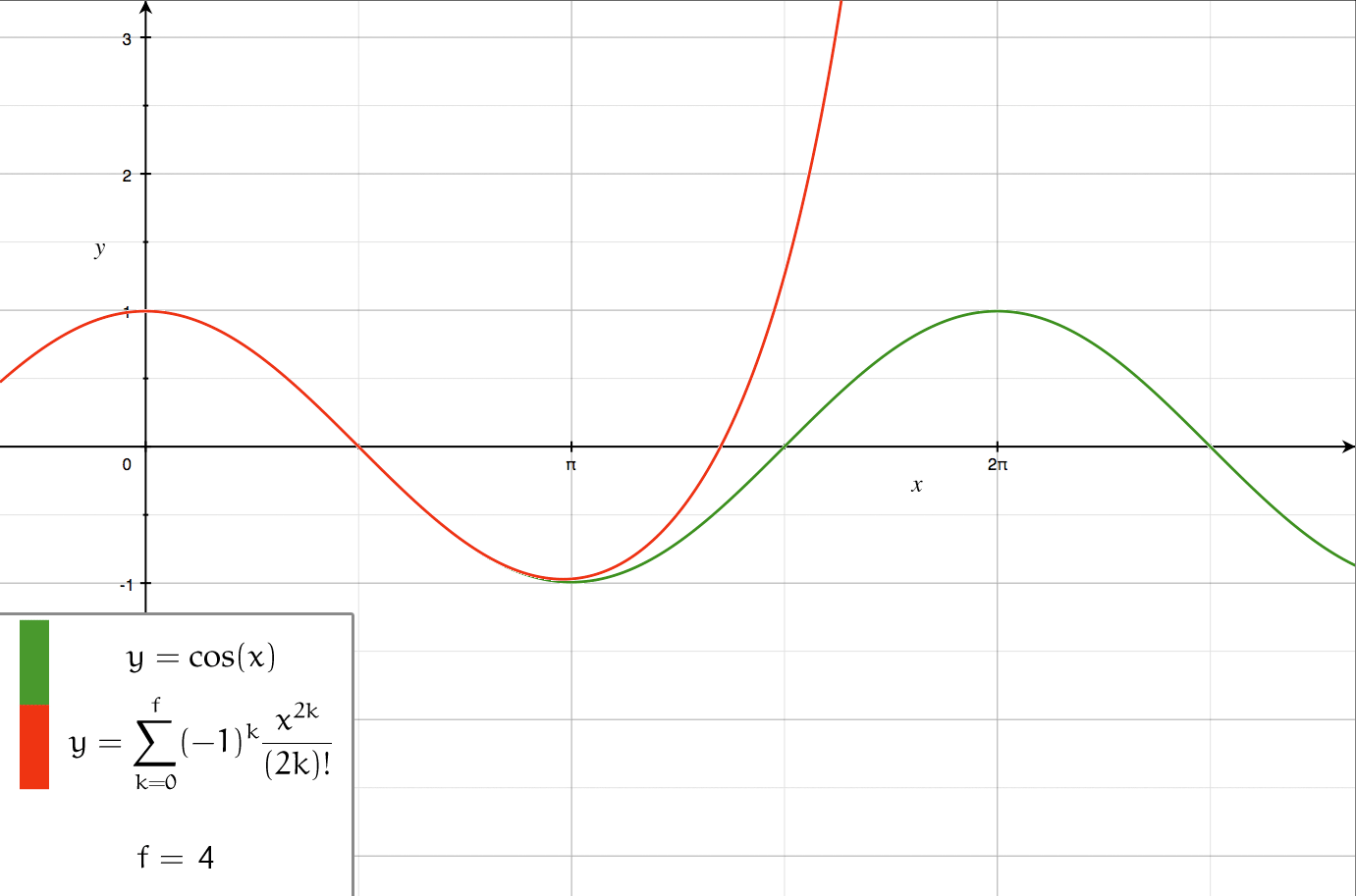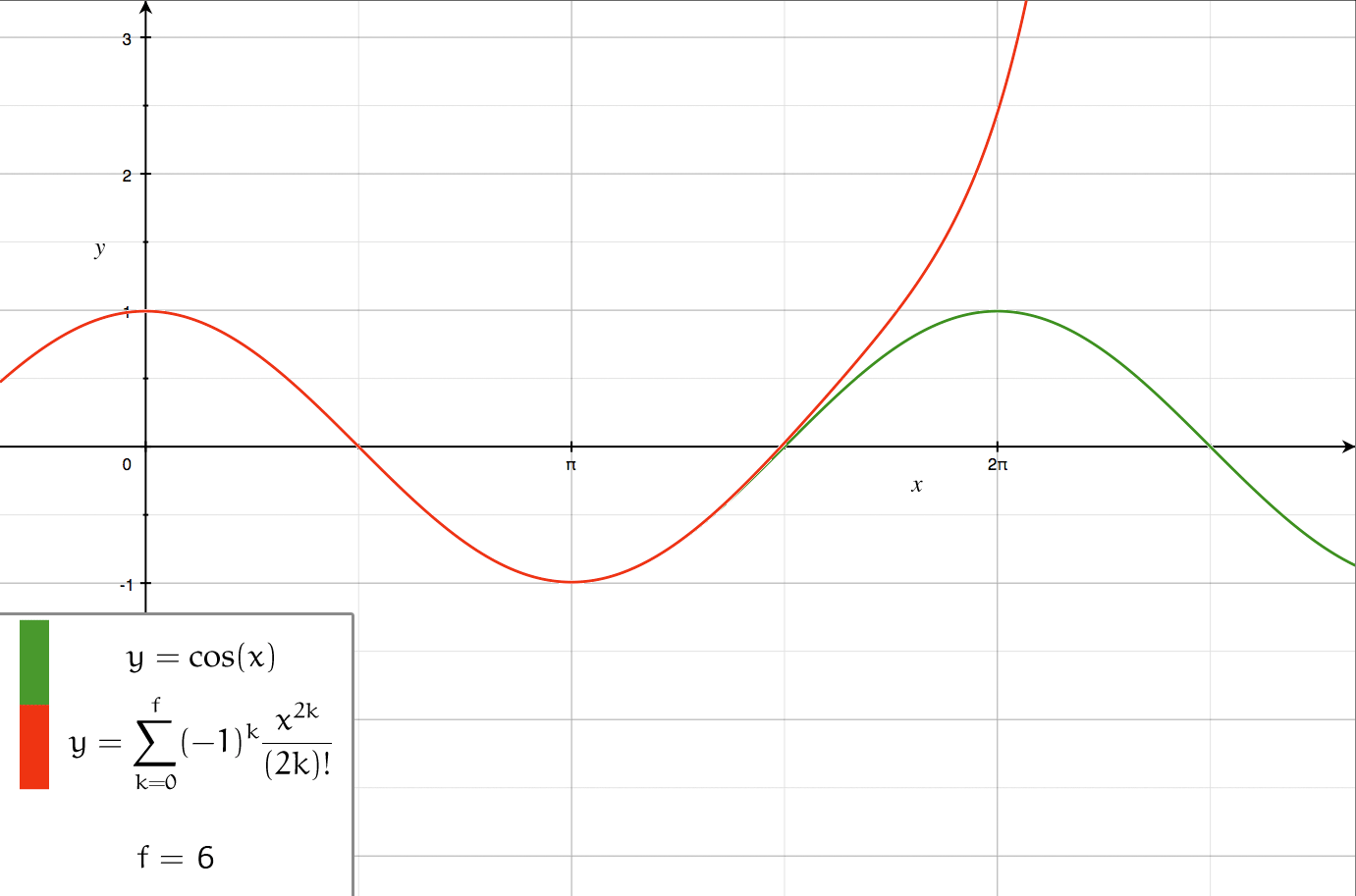
Series Expansion
In mathematics, a series expansion is an expansion of a function into a series, or infinite sum. It is a method for calculating a function that cannot be expressed by just elementary operators (addition, subtraction, multiplication and division). The resulting so-called '' series'' often can be limited to a finite number of terms, thus yielding an approximation of the function. The fewer terms of the sequence are used, the simpler this approximation will be. Often, the resulting inaccuracy (i.e., the partial sum of the omitted terms) can be described by an equation involving Big O notation (see also asymptotic expansion). The series expansion on an open interval will also be an approximation for non-analytic functions. Types of series expansions There are several kinds of series expansions, listed below. A ''Taylor series'' is a power series based on a function's derivatives at a single point. More specifically, if a function f: U\to\mathbb is infinitely differentiab ...
[...More Info...]       [...Related Items...]     OR:     [Wikipedia]   [Google]   [Baidu]