Deferent on:
[Wikipedia]
[Google]
[Amazon]
In the Hipparchian, Ptolemaic, and Copernican systems of
 In both Hipparchian and Ptolemaic systems, the
In both Hipparchian and Ptolemaic systems, the
 The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions. The introduction of better celestial measurement instruments, such as the introduction of the
The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions. The introduction of better celestial measurement instruments, such as the introduction of the 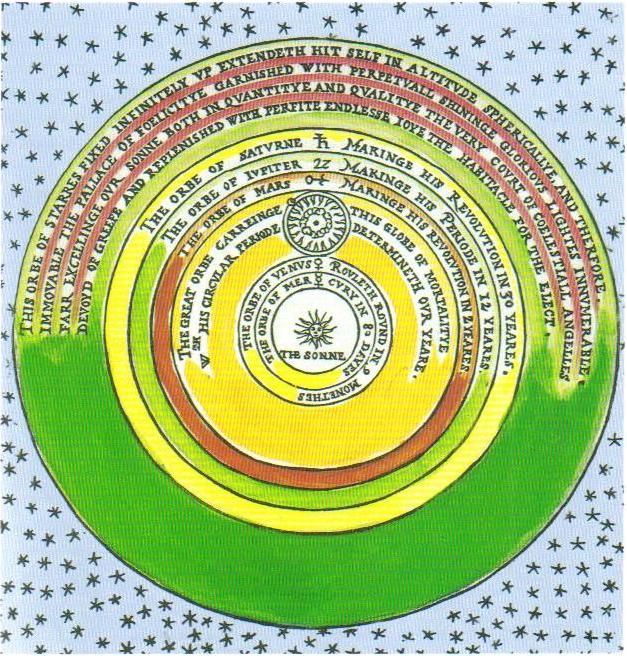 Owen Gingerich describes a planetary conjunction that occurred in 1504 and was apparently observed by Copernicus. In notes bound with his copy of the '' Alfonsine Tables'', Copernicus commented that "Mars surpasses the numbers by more than two degrees. Saturn is surpassed by the numbers by one and a half degrees." Using modern computer programs, Gingerich discovered that, at the time of the conjunction, Saturn indeed lagged behind the tables by a degree and a half and Mars led the predictions by nearly two degrees. Moreover, he found that Ptolemy's predictions for Jupiter at the same time were quite accurate. Copernicus and his contemporaries were therefore using Ptolemy's methods and finding them trustworthy well over a thousand years after Ptolemy's original work was published.
When Copernicus transformed Earth-based observations to heliocentric coordinates, he was confronted with an entirely new problem. The Sun-centered positions displayed a cyclical motion with respect to time but without retrograde loops in the case of the outer planets. In principle, the heliocentric motion was simpler but with new subtleties due to the yet-to-be-discovered elliptical shape of the orbits. Another complication was caused by a problem that Copernicus never solved: correctly accounting for the motion of the Earth in the coordinate transformation. In keeping with past practice, Copernicus used the deferent/epicycle model in his theory but his epicycles were small and were called "epicyclets".
In the Ptolemaic system the models for each of the planets were different, and so it was with Copernicus' initial models. As he worked through the mathematics, however, Copernicus discovered that his models could be combined in a unified system. Furthermore, if they were scaled so that the Earth's orbit was the same in all of them, the ordering of the planets we recognize today easily followed from the math. Mercury orbited closest to the Sun and the rest of the planets fell into place in order outward, arranged in distance by their periods of revolution.
Although Copernicus' models reduced the magnitude of the epicycles considerably, whether they were simpler than Ptolemy's is moot. Copernicus eliminated Ptolemy's somewhat-maligned equant but at a cost of additional epicycles. Various 16th-century books based on Ptolemy and Copernicus use about equal numbers of epicycles. The idea that Copernicus used only 34 circles in his system comes from his own statement in a preliminary unpublished sketch called the ''Commentariolus''. By the time he published ''
Owen Gingerich describes a planetary conjunction that occurred in 1504 and was apparently observed by Copernicus. In notes bound with his copy of the '' Alfonsine Tables'', Copernicus commented that "Mars surpasses the numbers by more than two degrees. Saturn is surpassed by the numbers by one and a half degrees." Using modern computer programs, Gingerich discovered that, at the time of the conjunction, Saturn indeed lagged behind the tables by a degree and a half and Mars led the predictions by nearly two degrees. Moreover, he found that Ptolemy's predictions for Jupiter at the same time were quite accurate. Copernicus and his contemporaries were therefore using Ptolemy's methods and finding them trustworthy well over a thousand years after Ptolemy's original work was published.
When Copernicus transformed Earth-based observations to heliocentric coordinates, he was confronted with an entirely new problem. The Sun-centered positions displayed a cyclical motion with respect to time but without retrograde loops in the case of the outer planets. In principle, the heliocentric motion was simpler but with new subtleties due to the yet-to-be-discovered elliptical shape of the orbits. Another complication was caused by a problem that Copernicus never solved: correctly accounting for the motion of the Earth in the coordinate transformation. In keeping with past practice, Copernicus used the deferent/epicycle model in his theory but his epicycles were small and were called "epicyclets".
In the Ptolemaic system the models for each of the planets were different, and so it was with Copernicus' initial models. As he worked through the mathematics, however, Copernicus discovered that his models could be combined in a unified system. Furthermore, if they were scaled so that the Earth's orbit was the same in all of them, the ordering of the planets we recognize today easily followed from the math. Mercury orbited closest to the Sun and the rest of the planets fell into place in order outward, arranged in distance by their periods of revolution.
Although Copernicus' models reduced the magnitude of the epicycles considerably, whether they were simpler than Ptolemy's is moot. Copernicus eliminated Ptolemy's somewhat-maligned equant but at a cost of additional epicycles. Various 16th-century books based on Ptolemy and Copernicus use about equal numbers of epicycles. The idea that Copernicus used only 34 circles in his system comes from his own statement in a preliminary unpublished sketch called the ''Commentariolus''. By the time he published '' Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today had
Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today had
Ptolemaic System
– at Rice University's Galileo Project
at MathPages
Ptolemaic System Simulator
interactive, Foothill College.
Orbits with Epicycles on a Deferent
interactive, Wolfram Demonstrations.
ANIMATE: Epicycles
interactive JavaScript coding example, Khan Academy.
Ptolemy and Homer (Simpson)
Reconstruction of a planet's bizarre orbit with Ptolemy's system of epicycles and deferents. {{Ancient Greek astronomy Ancient Greek astronomy pl:Deferent
astronomy
Astronomy () is a natural science that studies astronomical object, celestial objects and phenomena. It uses mathematics, physics, and chemistry in order to explain their origin and chronology of the Universe, evolution. Objects of interest ...
, the epicycle (, meaning "circle moving on another circle") was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon
The Moon is Earth's only natural satellite. It is the fifth largest satellite in the Solar System and the largest and most massive relative to its parent planet, with a diameter about one-quarter that of Earth (comparable to the width ...
, Sun, and planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a ...
s. In particular it explained the apparent retrograde motion
Apparent retrograde motion is the apparent motion of a planet in a direction opposite to that of other bodies within its system, as observed from a particular vantage point. Direct motion or prograde motion is motion in the same direction as ...
of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth.
It was first proposed by Apollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contribut ...
at the end of the 3rd century BC. It was developed by Apollonius of Perga and Hipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equ ...
of Rhodes, who used it extensively, during the 2nd century BC, then formalized and extensively used by Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of import ...
in his 2nd century AD astronomical treatise the ''Almagest
The ''Almagest'' is a 2nd-century Greek-language mathematical and astronomical treatise on the apparent motions of the stars and planetary paths, written by Claudius Ptolemy ( ). One of the most influential scientific texts in history, it cano ...
''.
Epicyclical motion is used in the Antikythera mechanism
The Antikythera mechanism ( ) is an Ancient Greek hand-powered orrery, described as the oldest example of an analogue computer used to predict astronomical positions and eclipses decades in advance. It could also be used to track the four-y ...
, an ancient Greek astronomical device for compensating for the elliptical orbit of the Moon, moving faster at perigee and slower at apogee than circular orbits would, using four gears, two of them engaged in an eccentric way that quite closely approximates Kepler's second law
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits ...
.
Epicycles worked very well and were highly accurate, because, as Fourier analysis later showed, any smooth curve can be approximated to arbitrary accuracy with a sufficient number of epicycles. However, they fell out of favor with the discovery that planetary motions were largely elliptical from a heliocentric frame of reference, which led to the discovery that gravity obeying a simple inverse square law could better explain all planetary motions.
Introduction
planet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a ...
s are assumed to move in a small circle called an ''epicycle'', which in turn moves along a larger circle called a ''deferent''. Both circles rotate clockwise and are roughly parallel to the plane of the Sun's apparent orbit under those systems (ecliptic
The ecliptic or ecliptic plane is the orbital plane of the Earth around the Sun. From the perspective of an observer on Earth, the Sun's movement around the celestial sphere over the course of a year traces out a path along the ecliptic agai ...
). Despite the fact that the system is considered geocentric
In astronomy, the geocentric model (also known as geocentrism, often exemplified specifically by the Ptolemaic system) is a superseded description of the Universe with Earth at the center. Under most geocentric models, the Sun, Moon, stars, an ...
, neither of the circles were exactly concentric with Earth. More specifically, each planet's motion was centered at a planet-specific point slightly away from the Earth called the ''eccentric''. The orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such a ...
s of planets in this system are similar to epitrochoids.
In the Hipparchian system the epicycle rotated and revolved along the deferent with uniform motion. However, Ptolemy found that he could not reconcile that with the Babylonian observational data available to him; in particular, the shape and size of the apparent retrogrades differed. The angular rate at which the epicycle traveled was not constant unless he measured it from another point which he called the ''equant
Equant (or punctum aequans) is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of the planets. The equant is used to explain the observed speed change in different stages of the plan ...
''. It was the angular rate at which the deferent moved around the point midway between the equant and the Earth (the eccentric) that was constant; the epicycle center swept out equal angles over equal times only when viewed from the equant. It was the use of equants to decouple uniform motion from the center of the circular deferents that distinguished the Ptolemaic system.
Ptolemy did not predict the relative sizes of the planetary deferents in the ''Almagest''. All of his calculations were done with respect to a normalized deferent, considering a single case at a time. This is not to say that he believed the planets were all equidistant, but he had no basis on which to measure distances, except for the Moon. He generally ordered the planets outward from the Earth based on their orbit periods. Later he calculated their distances in the ''Planetary Hypotheses
Planetary means relating to a planet or planets. It can also refer to:
;Science
* Planetary habitability, the measure of an astronomical body's potential to develop and sustain life
* Planetary nebula, an astronomical object
;People
* Planet ...
'' and summarized them in the first column of this table:
Had his values for deferent radii relative to the Earth–Sun distance been more accurate, the epicycle sizes would have all approached the Earth–Sun distance. Although all the planets are considered separately, in one peculiar way they were all linked: the lines drawn from the body through the epicentric center of all the planets were all parallel, along with the line drawn from the Sun to the Earth along which Mercury and Venus were situated. That means that all the bodies revolve in their epicycles in lockstep with Ptolemy's Sun (that is, they all have exactly a one-year period).
Babylonian observations showed that for superior planets the planet would typically move through in the night sky slower than the stars. Each night the planet appeared to lag a little behind the stars, in what is called prograde motion
Retrograde motion in astronomy is, in general, orbital or rotational motion of an object in the direction opposite the rotation of its primary, that is, the central object (right figure). It may also describe other motions such as precession or ...
. Near opposition, the planet would appear to reverse and move through the night sky faster than the stars for a time in retrograde motion
Retrograde motion in astronomy is, in general, orbital or rotational motion of an object in the direction opposite the rotation of its primary, that is, the central object (right figure). It may also describe other motions such as precession ...
before reversing again and resuming prograde. Epicyclic theory, in part, sought to explain this behavior.
The inferior planets were always observed to be near the Sun, appearing only shortly before sunrise or shortly after sunset. Their apparent retrograde motion occurs during the transition between evening star into morning star, as they pass between the Earth and the Sun.
History
When ancient astronomers viewed the sky, they saw the Sun, Moon, and stars moving overhead in a regular fashion. Babylonians did celestial observations, mainly of the sun and moon as a means of recalibrating and preserving timekeeping for religious ceremonies. Other early civilizations such as the Greeks had thinkers like Thales of Miletus, the first to document and predict a solar eclipse, or Heraclides, the earliest recorded astronomer to propose a geocentric model for the cosmos. They also saw the "wanderers" or ''"planetai"'' (ourplanet
A planet is a large, rounded astronomical body that is neither a star nor its remnant. The best available theory of planet formation is the nebular hypothesis, which posits that an interstellar cloud collapses out of a nebula to create a ...
s). The regularity in the motions of the wandering bodies suggested that their positions might be predictable.
 The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions. The introduction of better celestial measurement instruments, such as the introduction of the
The most obvious approach to the problem of predicting the motions of the heavenly bodies was simply to map their positions against the star field and then to fit mathematical functions to the changing positions. The introduction of better celestial measurement instruments, such as the introduction of the gnomon
A gnomon (; ) is the part of a sundial that casts a shadow. The term is used for a variety of purposes in mathematics and other fields.
History
A painted stick dating from 2300 BC that was excavated at the astronomical site of Taosi is the o ...
by Anaximander, allowed the Greeks to have a better understanding of the passage of time, such as the number of days in a year and the length of seasons, which are indispensable for astronomic measurements.
The ancients worked from a geocentric
In astronomy, the geocentric model (also known as geocentrism, often exemplified specifically by the Ptolemaic system) is a superseded description of the Universe with Earth at the center. Under most geocentric models, the Sun, Moon, stars, an ...
perspective for the simple reason that the Earth was where they stood and observed the sky, and it is the sky which appears to move while the ground seems still and steady underfoot. Some Greek astronomers (e.g., Aristarchus of Samos) speculated that the planets (Earth included) orbited the Sun, but the optics
Optics is the branch of physics that studies the behaviour and properties of light, including its interactions with matter and the construction of instruments that use or detect it. Optics usually describes the behaviour of visible, ultra ...
(and the specific mathematics – Isaac Newton
Sir Isaac Newton (25 December 1642 – 20 March 1726/27) was an English mathematician, physicist, astronomer, alchemist, theologian, and author (described in his time as a " natural philosopher"), widely recognised as one of the g ...
's law of gravitation for example) necessary to provide data that would convincingly support the heliocentric
Heliocentrism (also known as the Heliocentric model) is the astronomical model in which the Earth and planets revolve around the Sun at the center of the universe. Historically, heliocentrism was opposed to geocentrism, which placed the Earth ...
model did not exist in Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of import ...
's time and would not come around for over fifteen hundred years after his time. Furthermore, Aristotelian physics
Aristotelian physics is the form of natural science described in the works of the Greek philosopher Aristotle (384–322 BC). In his work ''Physics'', Aristotle intended to establish general principles of change that govern all natural bodies, ...
was not designed with these sorts of calculations in mind, and Aristotle
Aristotle (; grc-gre, Ἀριστοτέλης ''Aristotélēs'', ; 384–322 BC) was a Greek philosopher and polymath during the Classical Greece, Classical period in Ancient Greece. Taught by Plato, he was the founder of the Peripatet ...
's philosophy regarding the heavens was entirely at odds with the concept of heliocentrism. It was not until Galileo Galilei
Galileo di Vincenzo Bonaiuti de' Galilei (15 February 1564 – 8 January 1642) was an Italian astronomer, physicist and engineer, sometimes described as a polymath. Commonly referred to as Galileo, his name was pronounced (, ). He w ...
observed the moons of Jupiter
Jupiter is the fifth planet from the Sun and the largest in the Solar System. It is a gas giant with a mass more than two and a half times that of all the other planets in the Solar System combined, but slightly less than one-thousandt ...
on 7 January 1610, and the phases of Venus
Venus is the second planet from the Sun. It is sometimes called Earth's "sister" or "twin" planet as it is almost as large and has a similar composition. As an interior planet to Earth, Venus (like Mercury) appears in Earth's sky never f ...
in September 1610, that the heliocentric model began to receive broad support among astronomers, who also came to accept the notion that the planets are individual worlds orbiting the Sun (that is, that the Earth is a planet, too). Johannes Kepler formulated his three laws of planetary motion
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbit ...
, which describe the orbits of the planets in our solar system to a remarkable degree of accuracy utilizing a system that employs elliptical rather than circular orbits. Kepler's three laws are still taught today in university physics and astronomy classes, and the wording of these laws has not changed since Kepler first formulated them four hundred years ago.
The apparent motion of the heavenly bodies with respect to time is cyclical
Cycle, cycles, or cyclic may refer to:
Anthropology and social sciences
* Cyclic history, a theory of history
* Cyclical theory, a theory of American political history associated with Arthur Schlesinger, Sr.
* Social cycle, various cycles in soc ...
in nature. Apollonius of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contribut ...
realized that this cyclical variation could be represented visually by small circular orbits, or ''epicycles'', revolving on larger circular orbits, or ''deferents''. Hipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equ ...
calculated the required orbits. Deferents and epicycles in the ancient models did not represent orbits in the modern sense, but rather a complex set of circular paths whose centers are separated by a specific distance in order to approximate the observed movement of the celestial bodies.
Claudius Ptolemy refined the deferent-and-epicycle concept and introduced the equant
Equant (or punctum aequans) is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of the planets. The equant is used to explain the observed speed change in different stages of the plan ...
as a mechanism that accounts for velocity variations in the motions of the planets. The empirical
Empirical evidence for a proposition is evidence, i.e. what supports or counters this proposition, that is constituted by or accessible to sense experience or experimental procedure. Empirical evidence is of central importance to the sciences and ...
methodology he developed proved to be extraordinarily accurate for its day and was still in use at the time of Copernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formula ...
and Kepler. It is important to clarify that a heliocentric model is not necessarily more accurate as a system to track and predict the movements of celestial bodies than a geocentric one when considering strictly circular orbits. A heliocentric system would require more intricate systems to compensate for the shift in reference point. It was not until Kepler's proposal of elliptical orbits that such a system became increasingly more accurate than a mere epicyclical geocentric model.
De revolutionibus orbium coelestium
''De revolutionibus orbium coelestium'' (English translation: ''On the Revolutions of the Heavenly Spheres'') is the seminal work on the heliocentric theory of the astronomer Nicolaus Copernicus (1473–1543) of the Polish Renaissance. The boo ...
'', he had added more circles. Counting the total number is difficult, but estimates are that he created a system just as complicated, or even more so. Koestler, in his history of man's vision of the universe, equates the number of epicycles used by Copernicus at 48. The popular total of about 80 circles for the Ptolemaic system seems to have appeared in 1898. It may have been inspired by the ''non-Ptolemaic'' system of Girolamo Fracastoro, who used either 77 or 79 orbs in his system inspired by Eudoxus of Cnidus
Eudoxus of Cnidus (; grc, Εὔδοξος ὁ Κνίδιος, ''Eúdoxos ho Knídios''; ) was an ancient Greek astronomer, mathematician, scholar, and student of Archytas and Plato. All of his original works are lost, though some fragments a ...
. Copernicus in his works exaggerated the number of epicycles used in the Ptolemaic system; although original counts ranged to 80 circles, by Copernicus's time the Ptolemaic system had been updated by Peurbach toward the similar number of 40; hence Copernicus effectively replaced the problem of retrograde with further epicycles.
Copernicus' theory was at least as accurate as Ptolemy's but never achieved the stature and recognition of Ptolemy's theory. What was needed was Kepler's elliptical-orbit theory, not published until 1609 and 1619. Copernicus' work provided explanations for phenomena like retrograde motion, but really did not prove that the planets actually orbited the Sun.
 Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today had
Ptolemy's and Copernicus' theories proved the durability and adaptability of the deferent/epicycle device for representing planetary motion. The deferent/epicycle models worked as well as they did because of the extraordinary orbital stability of the solar system. Either theory could be used today had Gottfried Wilhelm Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mat ...
and Isaac Newton not invented calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematics, mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizati ...
.
According to Maimonides
Musa ibn Maimon (1138–1204), commonly known as Maimonides (); la, Moses Maimonides and also referred to by the acronym Rambam ( he, רמב״ם), was a Sephardic Jewish philosopher who became one of the most prolific and influential Torah ...
, the now-lost astronomical system of Ibn Bajjah
Abū Bakr Muḥammad ibn Yaḥyà ibn aṣ-Ṣā’igh at-Tūjībī ibn Bājja ( ar, أبو بكر محمد بن يحيى بن الصائغ التجيبي بن باجة), best known by his Latinised name Avempace (; – 1138), was an A ...
in 12th century Andalusian Spain
Andalusia (, ; es, Andalucía ) is the southernmost autonomous community in Peninsular Spain. It is the most populous and the second-largest autonomous community in the country. It is officially recognised as a "historical nationality". The ...
lacked epicycles. Gersonides
Levi ben Gershon (1288 – 20 April 1344), better known by his Graecized name as Gersonides, or by his Latinized name Magister Leo Hebraeus, or in Hebrew by the abbreviation of first letters as ''RaLBaG'', was a medieval French Jewish philosop ...
of 14th century France also eliminated epicycles, arguing that they did not align with his observations. Despite these alternative models, epicycles were not fully eliminated until the 17th century, when Johannes Kepler's model of elliptical orbits gradually replaced Copernicus' model based on perfect circles.
Newtonian or classical mechanics
Classical mechanics is a physical theory describing the motion of macroscopic objects, from projectiles to parts of machinery, and astronomical objects, such as spacecraft, planets, stars, and galaxies. For objects governed by classical ...
eliminated the need for deferent/epicycle methods altogether and produced more accurate theories. By treating the Sun and planets as point masses and using Newton's law of universal gravitation
Newton's law of universal gravitation is usually stated as that every particle attracts every other particle in the universe with a force that is proportional to the product of their masses and inversely proportional to the square of the distanc ...
, equations of motion were derived that could be solved by various means to compute predictions of planetary orbital velocities and positions. If approximated as simple two-body problem
In classical mechanics, the two-body problem is to predict the motion of two massive objects which are abstractly viewed as point particles. The problem assumes that the two objects interact only with one another; the only force affecting each ...
s, for example, they could be solved analytically, while the more realistic n-body problem required numerical methods for solution.
The power of Newtonian mechanics to solve problems in orbital mechanics is illustrated by the discovery of Neptune
The planet Neptune was mathematically predicted before it was directly observed. With a prediction by Urbain Le Verrier, telescopic observations confirming the existence of a major planet were made on the night of September 23–24, 1846, at the ...
. Analysis of observed perturbations in the orbit of Uranus
Uranus is the seventh planet from the Sun. Its name is a reference to the Greek god of the sky, Uranus (Caelus), who, according to Greek mythology, was the great-grandfather of Ares (Mars), grandfather of Zeus (Jupiter) and father of Cronu ...
produced estimates of the suspected planet's position within a degree of where it was found. This could not have been accomplished with deferent/epicycle methods. Still, Newton in 1702 published ''Theory of the Moon's Motion'' which employed an epicycle and remained in use in China into the nineteenth century. Subsequent tables based on Newton's ''Theory'' could have approached arcminute accuracy.
The number of epicycles
According to one school of thought in the history of astronomy, minor imperfections in the original Ptolemaic system were discovered through observations accumulated over time. It was mistakenly believed that more levels of epicycles (circles within circles) were added to the models to match more accurately the observed planetary motions. The multiplication of epicycles is believed to have led to a nearly unworkable system by the 16th century, and thatCopernicus
Nicolaus Copernicus (; pl, Mikołaj Kopernik; gml, Niklas Koppernigk, german: Nikolaus Kopernikus; 19 February 1473 – 24 May 1543) was a Renaissance polymath, active as a mathematician, astronomer, and Catholic canon, who formula ...
created his heliocentric system in order to simplify the Ptolemaic astronomy of his day, thus succeeding in drastically reducing the number of circles.
As a measure of complexity, the number of circles is given as 80 for Ptolemy, versus a mere 34 for Copernicus. The highest number appeared in the ''Encyclopædia Britannica
The ( Latin for "British Encyclopædia") is a general knowledge English-language encyclopaedia. It is published by Encyclopædia Britannica, Inc.; the company has existed since the 18th century, although it has changed ownership various ...
'' on Astronomy during the 1960s, in a discussion of King Alfonso X of Castile
Alfonso X (also known as the Wise, es, el Sabio; 23 November 1221 – 4 April 1284) was King of Castile, León and Kingdom of Galicia, Galicia from 30 May 1252 until his death in 1284. During the April 1257 Imperial election, election of 1257, ...
's interest in astronomy during the 13th century. (Alfonso is credited with commissioning the Alfonsine Tables.)
As it turns out, a major difficulty with this epicycles-on-epicycles theory is that historians examining books on Ptolemaic astronomy from the Middle Ages and the Renaissance have found absolutely no trace of multiple epicycles being used for each planet. The Alfonsine Tables, for instance, were apparently computed using Ptolemy's original unadorned methods.
Another problem is that the models themselves discouraged tinkering. In a deferent-and-epicycle model, the parts of the whole are interrelated. A change in a parameter to improve the fit in one place would throw off the fit somewhere else. Ptolemy's model is probably optimal in this regard. On the whole it gave good results but missed a little here and there. Experienced astronomers would have recognized these shortcomings and allowed for them.
Mathematical formalism
According to the historian of scienceNorwood Russell Hanson
Norwood Russell Hanson (August 17, 1924 – April 18, 1967) was an American philosopher of science. Hanson was a pioneer in advancing the argument that observation is theory-laden — that observation language and theory language are deeply inte ...
:
Any path—periodic or not, closed or open—can be represented with an infinite number of epicycles. This is because epicycles can be represented as a complex Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or '' ...
; therefore, with a large number of epicycles, very complex paths can be represented in the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
.
Let the complex number
where and are constants, is the imaginary unit
The imaginary unit or unit imaginary number () is a solution to the quadratic equation x^2+1=0. Although there is no real number with this property, can be used to extend the real numbers to what are called complex numbers, using addition a ...
, and is time, correspond to a deferent centered on the origin of the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
and revolving with a radius and angular velocity
In physics, angular velocity or rotational velocity ( or ), also known as angular frequency vector,(UP1) is a pseudovector representation of how fast the angular position or orientation of an object changes with time (i.e. how quickly an objec ...
where is the period.
If is the path of an epicycle, then the deferent plus epicycle is represented as the sum
This is an almost periodic function, and is a periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to d ...
just when the ratio of the constants is rational
Rationality is the quality of being guided by or based on reasons. In this regard, a person acts rationally if they have a good reason for what they do or a belief is rational if it is based on strong evidence. This quality can apply to an abil ...
. Generalizing to epicycles yields the almost periodic function
which is periodic just when every pair of is rationally related. Finding the coefficients to represent a time-dependent path in the complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by th ...
, , is the goal of reproducing an orbit with deferent and epicycles, and this is a way of "saving the phenomena Scientific formalism is a family of approaches to the presentation of science. It is viewed as an important part of the scientific method, especially in the physical sciences.
Levels of formalism
There are multiple levels of scientific formalism p ...
" (σώζειν τα φαινόμενα).
This parallel was noted by Giovanni Schiaparelli
Giovanni Virginio Schiaparelli ( , also , ; 14 March 1835 – 4 July 1910) was an Italian astronomer and science historian.
Biography
He studied at the University of Turin, graduating in 1854, and later did research at Berlin Observatory ...
. Pertinent to the Copernican Revolution's debate about "saving the phenomena Scientific formalism is a family of approaches to the presentation of science. It is viewed as an important part of the scientific method, especially in the physical sciences.
Levels of formalism
There are multiple levels of scientific formalism p ...
" versus offering explanations, one can understand why Thomas Aquinas
Thomas Aquinas, OP (; it, Tommaso d'Aquino, lit=Thomas of Aquino; 1225 – 7 March 1274) was an Italian Dominican friar and priest who was an influential philosopher, theologian and jurist in the tradition of scholasticism; he is known wi ...
, in the 13th century, wrote:
Epicycles and the Catholic Church
Being a system that was for the most part used to justify the geocentric model, with the exception of Copernicus' cosmos, the deferent and epicycle model was favored over the heliocentric ideas that Kepler and Galileo proposed. The church endorsed this model as it favored its central dogma. Later adopters of the epicyclic model such asTycho Brahe
Tycho Brahe ( ; born Tyge Ottesen Brahe; generally called Tycho (14 December 154624 October 1601) was a Danish astronomer, known for his comprehensive astronomical observations, generally considered to be the most accurate of his time. He was ...
, who considered the Church's scriptures when creating his model, were seen even more favorably. The Tychonic model was a hybrid model that blended the geocentric and heliocentric characteristics, with a still Earth that has the sun and moon surrounding it, and the planets orbiting the sun. To Brahe, the idea of a revolving and moving Earth was impossible, and the scripture should be always paramount and respected. When Galileo tried to challenge Tycho Brahe's system, the church was dissatisfied with their views being challenged. Galileo's publication did not aid his case in his trial.
Bad science
"Adding epicycles" has come to be used as a derogatory comment in modern scientific discussion. The term might be used, for example, to describe continuing to try to adjust a theory to make its predictions match the facts. There is a generally accepted idea that extra epicycles were invented to alleviate the growing errors that the Ptolemaic system noted as measurements became more accurate, particularly for Mars. According to this notion, epicycles are regarded by some as the paradigmatic example of bad science. Copernicus added an extra epicycle to his planets, but that was only in an effort to eliminate Ptolemy's equant, which he considered a philosophical break away from Aristotle's perfection of the heavens. Mathematically, the second epicycle and the equant produce the same results, and many Copernican astronomers before Kepler continued using the equant, as the mathematical calculations were easier. Copernicus' epicycles were also much smaller than Ptolemy's, and were required because the planets in his model moved in perfect circles. Johannes Kepler would later show that the planets move in ellipses, which removed the need for Copernicus' epicycles as well.See also
*Analemma
In astronomy, an analemma (; ) is a diagram showing the position of the Sun in the sky as seen from a fixed location on Earth at the same mean solar time, as that position varies over the course of a year. The diagram will resemble a figu ...
* Epicycloid
* Occam's razor
Occam's razor, Ockham's razor, or Ocham's razor ( la, novacula Occami), also known as the principle of parsimony or the law of parsimony ( la, lex parsimoniae), is the problem-solving principle that "entities should not be multiplied beyond neces ...
* Overfitting
mathematical modeling, overfitting is "the production of an analysis that corresponds too closely or exactly to a particular set of data, and may therefore fail to fit to additional data or predict future observations reliably". An overfitt ...
* Scientific method
The scientific method is an Empirical evidence, empirical method for acquiring knowledge that has characterized the development of science since at least the 17th century (with notable practitioners in previous centuries; see the article hist ...
Notes
External links
Ptolemaic System
– at Rice University's Galileo Project
at MathPages
Animated illustrations
Ptolemaic System Simulator
interactive, Foothill College.
Orbits with Epicycles on a Deferent
interactive, Wolfram Demonstrations.
ANIMATE: Epicycles
interactive JavaScript coding example, Khan Academy.
Ptolemy and Homer (Simpson)
Reconstruction of a planet's bizarre orbit with Ptolemy's system of epicycles and deferents. {{Ancient Greek astronomy Ancient Greek astronomy pl:Deferent