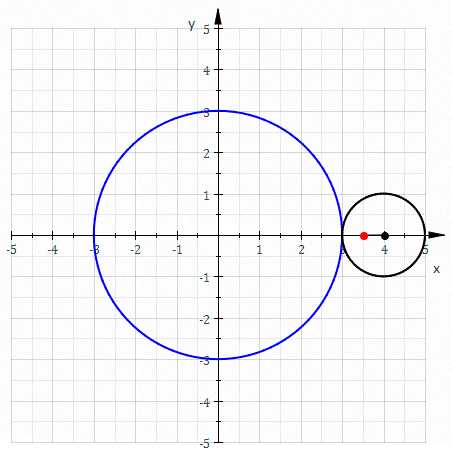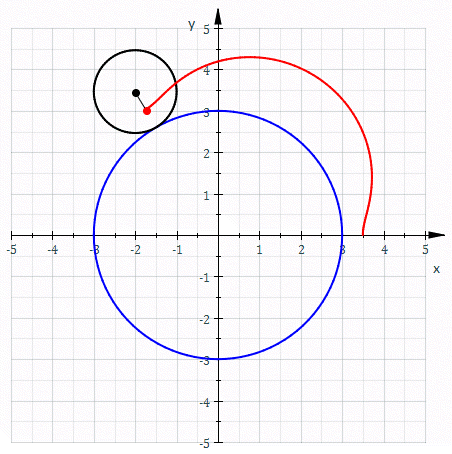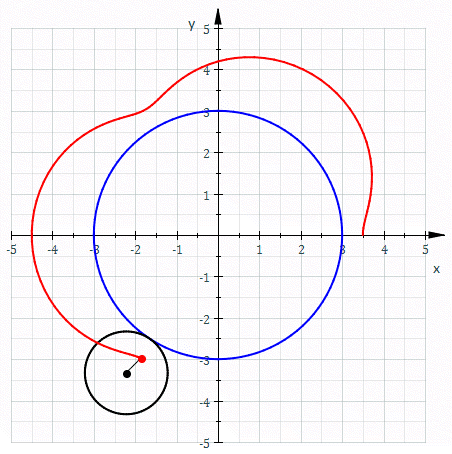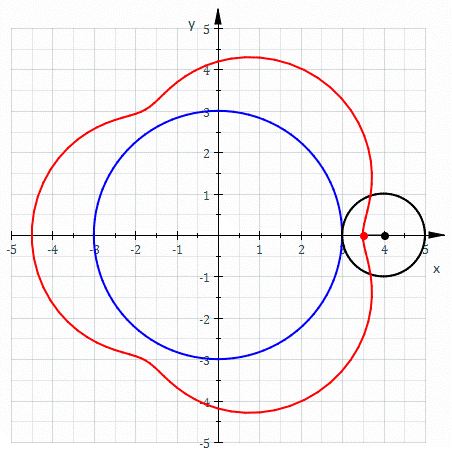
|
Deferent
In the Hipparchian, Ptolemaic, and Copernican systems of astronomy, the epicycle (, meaning "circle moving on another circle") was a geometric model used to explain the variations in speed and direction of the apparent motion of the Moon, Sun, and planets. In particular it explained the apparent retrograde motion of the five planets known at the time. Secondarily, it also explained changes in the apparent distances of the planets from the Earth. It was first proposed by Apollonius of Perga at the end of the 3rd century BC. It was developed by Apollonius of Perga and Hipparchus of Rhodes, who used it extensively, during the 2nd century BC, then formalized and extensively used by Ptolemy in his 2nd century AD astronomical treatise the ''Almagest''. Epicyclical motion is used in the Antikythera mechanism, an ancient Greek astronomical device for compensating for the elliptical orbit of the Moon, moving faster at perigee and slower at apogee than circular orbits would, using fou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Equant
Equant (or punctum aequans) is a mathematical concept developed by Claudius Ptolemy in the 2nd century AD to account for the observed motion of the planets. The equant is used to explain the observed speed change in different stages of the planetary orbit. This planetary concept allowed Ptolemy to keep the theory of uniform circular motion alive by stating that the path of heavenly bodies was uniform around one point and circular around another point. Placement The equant point (shown in the diagram by the large • ), is placed so that it is directly opposite to Earth from the deferent's center, known as the ''eccentric'' (represented by the × ). A planet or the center of an epicycle (a smaller circle carrying the planet) was conceived to move at a constant angular speed with respect to the equant. In other words, to a hypothetical observer placed at the equant point, the epicycle's center (indicated by the small · ) would appear to move at a st ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geocentric
In astronomy, the geocentric model (also known as geocentrism, often exemplified specifically by the Ptolemaic system) is a superseded description of the Universe with Earth at the center. Under most geocentric models, the Sun, Moon, stars, and planets all orbit Earth. The geocentric model was the predominant description of the cosmos in many European ancient civilizations, such as those of Aristotle in Classical Greece and Ptolemy in Roman Egypt. Two observations supported the idea that Earth was the center of the Universe: * First, from anywhere on Earth, the Sun appears to revolve around Earth once per day. While the Moon and the planets have their own motions, they also appear to revolve around Earth about once per day. The stars appeared to be fixed on a celestial sphere rotating once each day about an axis through the geographic poles of Earth. * Second, Earth seems to be unmoving from the perspective of an earthbound observer; it feels solid, stable, and stationary. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ptolemaic System
In astronomy, the geocentric model (also known as geocentrism, often exemplified specifically by the Ptolemaic system) is a superseded description of the Universe with Earth at the center. Under most geocentric models, the Sun, Moon, stars, and planets all orbit Earth. The geocentric model was the predominant description of the cosmos in many European ancient civilizations, such as those of Aristotle in Classical Greece and Ptolemy in Roman Egypt. Two observations supported the idea that Earth was the center of the Universe: * First, from anywhere on Earth, the Sun appears to revolve around Earth once per day. While the Moon and the planets have their own motions, they also appear to revolve around Earth about once per day. The stars appeared to be fixed on a celestial sphere rotating once each day about an axis through the geographic poles of Earth. * Second, Earth seems to be unmoving from the perspective of an earthbound observer; it feels solid, stable, and stationary. An ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Almagest
The ''Almagest'' is a 2nd-century Greek-language mathematical and astronomical treatise on the apparent motions of the stars and planetary paths, written by Claudius Ptolemy ( ). One of the most influential scientific texts in history, it canonized a geocentric model of the Universe that was accepted for more than 1,200 years from its origin in Hellenistic Alexandria, in the medieval Byzantine and Islamic worlds, and in Western Europe through the Middle Ages and early Renaissance until Copernicus. It is also a key source of information about ancient Greek astronomy. Ptolemy set up a public inscription at Canopus, Egypt, in 147 or 148. N. T. Hamilton found that the version of Ptolemy's models set out in the ''Canopic Inscription'' was earlier than the version in the ''Almagest''. Hence the ''Almagest'' could not have been completed before about 150, a quarter-century after Ptolemy began observing. Names The name comes from Arabic ', with ' meaning "the", and ''magesti'' bei ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equinoxes. Hipparchus was born in Nicaea, Bithynia, and probably died on the island of Rhodes, Greece. He is known to have been a working astronomer between 162 and 127 BC. Hipparchus is considered the greatest ancient astronomical observer and, by some, the greatest overall astronomer of antiquity. He was the first whose quantitative and accurate models for the motion of the Sun and Moon survive. For this he certainly made use of the observations and perhaps the mathematical techniques accumulated over centuries by the Babylonians and by Meton of Athens (fifth century BC), Timocharis, Aristyllus, Aristarchus of Samos, and Eratosthenes, among others. He developed trigonometry and constructed trigonometric tables, and he solved sever ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Copernican Heliocentrism
Copernican heliocentrism is the astronomical model developed by Nicolaus Copernicus and published in 1543. This model positioned the Sun at the center of the Universe, motionless, with Earth and the other planets orbiting around it in circular paths, modified by epicycles, and at uniform speeds. The Copernican model displaced the geocentric model of Ptolemy that had prevailed for centuries, which had placed Earth at the center of the Universe. Although he had circulated an outline of his own heliocentric theory to colleagues sometime before 1514, he did not decide to publish it until he was urged to do so later by his pupil Rheticus. Copernicus's challenge was to present a practical alternative to the Ptolemaic model by more elegantly and accurately determining the length of a solar year while preserving the metaphysical implications of a mathematically ordered cosmos. Thus, his heliocentric model retained several of the Ptolemaic elements, causing inaccuracies, such as the pla ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apparent Retrograde Motion
Apparent retrograde motion is the apparent motion of a planet in a direction opposite to that of other bodies within its system, as observed from a particular vantage point. Direct motion or prograde motion is motion in the same direction as other bodies. While the terms ''direct'' and ''prograde'' are equivalent in this context, the former is the traditional term in astronomy. The earliest recorded use of ''prograde'' was in the early 18th century, although the term is now less common. Etymology The term ''retrograde'' is from the Latin word – "backward-step", the affix meaning "backwards" and "step". ''Retrograde'' is most commonly an adjective used to describe the path of a planet as it travels through the night sky, with respect to the zodiac, stars, and other bodies of the celestial canopy. In this context, the term refers to planets, as they appear from Earth, stopping briefly and reversing direction at certain times, though in reality, of course, we now understa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apollonius Of Perga
Apollonius of Perga ( grc-gre, Ἀπολλώνιος ὁ Περγαῖος, Apollṓnios ho Pergaîos; la, Apollonius Pergaeus; ) was an Ancient Greek geometer and astronomer known for his work on conic sections. Beginning from the contributions of Euclid and Archimedes on the topic, he brought them to the state prior to the invention of analytic geometry. His definitions of the terms ellipse, parabola, and hyperbola are the ones in use today. Gottfried Wilhelm Leibniz stated “He who understands Archimedes and Apollonius will admire less the achievements of the foremost men of later times.” Apollonius worked on numerous other topics, including astronomy. Most of this work has not survived, where exceptions are typically fragments referenced by other authors like Pappus of Alexandria. His hypothesis of eccentric orbits to explain the apparently aberrant motion of the planets, commonly believed until the Middle Ages, was superseded during the Renaissance. The Apollonius crat ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kepler's Second Law
In astronomy, Kepler's laws of planetary motion, published by Johannes Kepler between 1609 and 1619, describe the orbits of planets around the Sun. The laws modified the heliocentric theory of Nicolaus Copernicus, replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary. The three laws state that: # The orbit of a planet is an ellipse with the Sun at one of the two foci. # A line segment joining a planet and the Sun sweeps out equal areas during equal intervals of time. # The square of a planet's orbital period is proportional to the cube of the length of the semi-major axis of its orbit. The elliptical orbits of planets were indicated by calculations of the orbit of Mars. From this, Kepler inferred that other bodies in the Solar System, including those farther away from the Sun, also have elliptical orbits. The second law helps to establish that when a planet is closer to the Sun, it travels faster. The third law e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier Analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Joseph Fourier, who showed that representing a function as a sum of trigonometric functions greatly simplifies the study of heat transfer. The subject of Fourier analysis encompasses a vast spectrum of mathematics. In the sciences and engineering, the process of decomposing a function into oscillatory components is often called Fourier analysis, while the operation of rebuilding the function from these pieces is known as Fourier synthesis. For example, determining what component frequencies are present in a musical note would involve computing the Fourier transform of a sampled musical note. One could then re-synthesize the same sound by including the frequency components as revealed in the Fourier analysis. In mathematics, the term ''Fourier ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orbit
In celestial mechanics, an orbit is the curved trajectory of an object such as the trajectory of a planet around a star, or of a natural satellite around a planet, or of an artificial satellite around an object or position in space such as a planet, moon, asteroid, or Lagrange point. Normally, orbit refers to a regularly repeating trajectory, although it may also refer to a non-repeating trajectory. To a close approximation, planets and satellites follow elliptic orbits, with the center of mass being orbited at a focal point of the ellipse, as described by Kepler's laws of planetary motion. For most situations, orbital motion is adequately approximated by Newtonian mechanics, which explains gravity as a force obeying an inverse-square law. However, Albert Einstein's general theory of relativity, which accounts for gravity as due to curvature of spacetime, with orbits following geodesics, provides a more accurate calculation and understanding of the exact mechanics of orbi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Epitrochoid
In geometry, an epitrochoid ( or ) is a roulette traced by a point attached to a circle of radius rolling around the outside of a fixed circle of radius , where the point is at a distance from the center of the exterior circle. The parametric equations for an epitrochoid are :\begin & x (\theta) = (R + r)\cos\theta - d\cos\left(\theta\right) \\ & y (\theta) = (R + r)\sin\theta - d\sin\left(\theta\right) \end The parameter is geometrically the polar angle of the center of the exterior circle. (However, is not the polar angle of the point (x(\theta),y(\theta)) on the epitrochoid.) Special cases include the limaçon with and the epicycloid with . The classic Spirograph toy traces out epitrochoid and hypotrochoid curves. The orbits of planets in the once popular geocentric Ptolemaic system are epitrochoids (see deferent and epicycle). The orbit of the moon, when centered around the sun, approximates an epitrochoid. The combustion chamber of the Wankel engine is an epitroch ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.png "Click for more on -> Fourier Analysis")
