Cubic Number on:
[Wikipedia]
[Google]
[Amazon]
In arithmetic and
 Proofs.
gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity
:
That identity is related to
Proofs.
gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity
:
That identity is related to 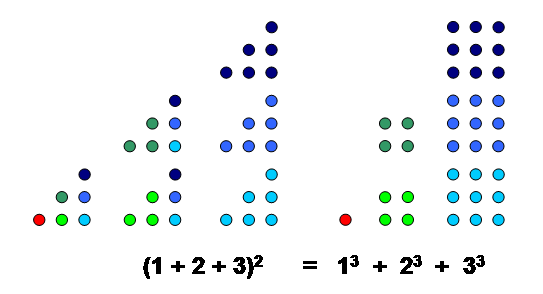 In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first
In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first
 There are examples of cubes of numbers in
There are examples of cubes of numbers in
algebra
Algebra () is one of the broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathematics.
Elementary ...
, the cube of a number is its third power
Power most often refers to:
* Power (physics), meaning "rate of doing work"
** Engine power, the power put out by an engine
** Electric power
* Power (social and political), the ability to influence people or events
** Abusive power
Power may a ...
, that is, the result of multiplying three instances of together.
The cube of a number or any other mathematical expression
In mathematics, an expression or mathematical expression is a finite combination of symbols that is well-formed according to rules that depend on the context. Mathematical symbols can designate numbers ( constants), variables, operations, f ...
is denoted by a superscript 3, for example or .
The cube is also the number multiplied by its square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90- degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length a ...
:
:.
The ''cube function'' is the function
Function or functionality may refer to:
Computing
* Function key, a type of key on computer keyboards
* Function model, a structured representation of processes in a system
* Function object or functor or functionoid, a concept of object-oriente ...
(often denoted ) that maps a number to its cube. It is an odd function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power se ...
, as
:.
The volume
Volume is a measure of occupied three-dimensional space. It is often quantified numerically using SI derived units (such as the cubic metre and litre) or by various imperial or US customary units (such as the gallon, quart, cubic inch). Th ...
of a geometric cube is the cube of its side length, giving rise to the name. The inverse operation that consists of finding a number whose cube is is called extracting the cube root of . It determines the side of the cube of a given volume. It is also raised to the one-third power.
The graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
of the cube function is known as the cubic parabola. Because the cube function is an odd function, this curve has a center of symmetry A fixed point of an isometry group is a point that is a fixed point for every isometry in the group. For any isometry group in Euclidean space the set of fixed points is either empty or an affine space.
For an object, any unique centre and, more ...
at the origin, but no axis of symmetry
Axial symmetry is symmetry around an axis; an object is axially symmetric if its appearance is unchanged if rotated around an axis.
.
In integers
A cube number, or a perfect cube, or sometimes just a cube, is a number which is the cube of aninteger
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
.
The non-negative perfect cubes up to 603 are :
Geometrically speaking, a positive integer is a perfect cube if and only if
In logic and related fields such as mathematics and philosophy, "if and only if" (shortened as "iff") is a biconditional logical connective between statements, where either both statements are true or both are false.
The connective is b ...
one can arrange solid unit cubes into a larger, solid cube. For example, 27 small cubes can be arranged into one larger one with the appearance of a Rubik's Cube, since .
The difference between the cubes of consecutive integers can be expressed as follows:
:.
or
:.
There is no minimum perfect cube, since the cube of a negative integer is negative. For example, .
Base ten
Unlikeperfect squares
In mathematics, a square number or perfect square is an integer that is the square of an integer; in other words, it is the product of some integer with itself. For example, 9 is a square number, since it equals and can be written as .
The usu ...
, perfect cubes do not have a small number of possibilities for the last two digits. Except for cubes divisible by 5, where only 25, 75 and 00 can be the last two digits, ''any'' pair of digits with the last digit odd can occur as the last digits of a perfect cube. With even
Even may refer to:
General
* Even (given name), a Norwegian male personal name
* Even (surname)
* Even (people), an ethnic group from Siberia and Russian Far East
** Even language, a language spoken by the Evens
* Odd and Even, a solitaire game w ...
cubes, there is considerable restriction, for only 00, 2, 4, 6 and 8 can be the last two digits of a perfect cube (where stands for any odd digit and for any even digit). Some cube numbers are also square numbers; for example, 64 is a square number and a cube number . This happens if and only if the number is a perfect sixth power (in this case 2).
The last digits of each 3rd power are:
It is, however, easy to show that most numbers are not perfect cubes because ''all'' perfect cubes must have digital root
The digital root (also repeated digital sum) of a natural number in a given radix is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit su ...
1, 8 or 9. That is their values modulo 9 may be only 0, 1, and 8. Moreover, the digital root of any number's cube can be determined by the remainder the number gives when divided by 3:
* If the number ''x'' is divisible by 3, its cube has digital root 9; that is,
*:
* If it has a remainder of 1 when divided by 3, its cube has digital root 1; that is,
*:
* If it has a remainder of 2 when divided by 3, its cube has digital root 8; that is,
*:
Waring's problem for cubes
Every positive integer can be written as the sum of nine (or fewer) positive cubes. This upper limit of nine cubes cannot be reduced because, for example, 23 cannot be written as the sum of fewer than nine positive cubes: :23 = 23 + 23 + 13 + 13 + 13 + 13 + 13 + 13 + 13.Sums of three cubes
It is conjectured that every integer (positive or negative) notcongruent
Congruence may refer to:
Mathematics
* Congruence (geometry), being the same size and shape
* Congruence or congruence relation, in abstract algebra, an equivalence relation on an algebraic structure that is compatible with the structure
* In mod ...
to modulo can be written as a sum of three (positive or negative) cubes with infinitely many ways. For example, . Integers congruent to modulo are excluded because they cannot be written as the sum of three cubes.
The smallest such integer for which such a sum is not known is 114. In September 2019, the previous smallest such integer with no known 3-cube sum, 42, was found to satisfy this equation:
:
One solution to is given in the table below for , and not congruent to or modulo . The selected solution is the one that is primitive (), is not of the form or (since they are infinite families of solutions), satisfies , and has minimal values for and (tested in this order).
Only primitive solutions are selected since the non-primitive ones can be trivially deduced from solutions for a smaller value of . For example, for , the solution results from the solution by multiplying everything by Therefore, this is another solution that is selected. Similarly, for , the solution is excluded, and this is the solution that is selected.
Fermat's Last Theorem for cubes
The equation has no non-trivial (i.e. ) solutions in integers. In fact, it has none inEisenstein integers
In mathematics, the Eisenstein integers (named after Gotthold Eisenstein), occasionally also known as Eulerian integers (after Leonhard Euler), are the complex numbers of the form
:z = a + b\omega ,
where and are integers and
:\omega = \f ...
.
Both of these statements are also true for the equation .
Sum of first ''n'' cubes
The sum of the first cubes is the thtriangle number
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots in ...
squared:
:
triangular numbers
A triangular number or triangle number counts objects arranged in an equilateral triangle. Triangular numbers are a type of figurate number, other examples being square numbers and cube numbers. The th triangular number is the number of dots i ...
in the following way:
:
and thus the summands forming start off just after those forming all previous values up to .
Applying this property, along with another well-known identity:
:
we obtain the following derivation:
:
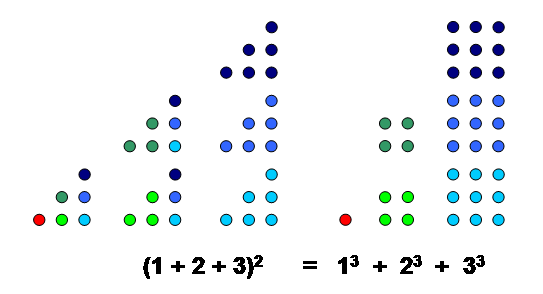 In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first
In the more recent mathematical literature, uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also ); he observes that it may also be proved easily (but uninformatively) by induction, and states that provides "an interesting old Arabic proof". provides a purely visual proof, provide two additional proofs, and gives seven geometric proofs.
For example, the sum of the first 5 cubes is the square of the 5th triangular number,
:
A similar result can be given for the sum of the first odd
Odd means unpaired, occasional, strange or unusual, or a person who is viewed as eccentric.
Odd may also refer to:
Acronym
* ODD (Text Encoding Initiative) ("One Document Does it all"), an abstracted literate-programming format for describing X ...
cubes,
:
but , must satisfy the negative Pell equation
Pell's equation, also called the Pell–Fermat equation, is any Diophantine equation of the form x^2 - ny^2 = 1, where ''n'' is a given positive nonsquare integer, and integer solutions are sought for ''x'' and ''y''. In Cartesian coordinates, ...
. For example, for and , then,
:
:
and so on. Also, every even
Even may refer to:
General
* Even (given name), a Norwegian male personal name
* Even (surname)
* Even (people), an ethnic group from Siberia and Russian Far East
** Even language, a language spoken by the Evens
* Odd and Even, a solitaire game w ...
perfect number
In number theory, a perfect number is a positive integer that is equal to the sum of its positive divisors, excluding the number itself. For instance, 6 has divisors 1, 2 and 3 (excluding itself), and 1 + 2 + 3 = 6, so 6 is a perfect number.
T ...
, except the lowest, is the sum of the first odd cubes (''p'' = 3, 5, 7, ...):
:
:
:
Sum of cubes of numbers in arithmetic progression
arithmetic progression
An arithmetic progression or arithmetic sequence () is a sequence of numbers such that the difference between the consecutive terms is constant. For instance, the sequence 5, 7, 9, 11, 13, 15, . . . is an arithmetic progression with a common differ ...
whose sum is a cube:
:
:
:
with the first one sometimes identified as the mysterious Plato's number
Plato's number is a number enigmatically referred to by Plato in his dialogue the ''Republic'' (8.546b). The text is notoriously difficult to understand and its corresponding translations do not allow an unambiguous interpretation. There is no rea ...
. The formula for finding the sum of
cubes of numbers in arithmetic progression with common difference and initial cube ,
:
is given by
:
A parametric solution to
:
is known for the special case of , or consecutive cubes, but only sporadic solutions are known for integer , such as = 2, 3, 5, 7, 11, 13, 37, 39, etc.
Cubes as sums of successive odd integers
In the sequence of odd integers 1, 3, 5, 7, 9, 11, 13, 15, 17, 19, ..., the first ''one'' is a cube (); the sum of the next ''two'' is the next cube (); the sum of the next ''three'' is the next cube (); and so forth.In rational numbers
Every positiverational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
is the sum of three positive rational cubes, and there are rationals that are not the sum of two rational cubes.
In real numbers, other fields, and rings
Inreal number
In mathematics, a real number is a number that can be used to measure a ''continuous'' one-dimensional quantity such as a distance, duration or temperature. Here, ''continuous'' means that values can have arbitrarily small variations. Every ...
s, the cube function preserves the order: larger numbers have larger cubes. In other words, cubes (strictly) monotonically increase. Also, its codomain
In mathematics, the codomain or set of destination of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation . The term range is sometimes ambiguously used to refer to either th ...
is the entire real line: the function is a surjection
In mathematics, a surjective function (also known as surjection, or onto function) is a function that every element can be mapped from element so that . In other words, every element of the function's codomain is the image of one element of ...
(takes all possible values). Only three numbers are equal to their own cubes: , , and . If or , then . If or , then . All aforementioned properties pertain also to any higher odd power (, , ...) of real numbers. Equalities and inequalities
Inequality may refer to:
Economics
* Attention inequality, unequal distribution of attention across users, groups of people, issues in etc. in attention economy
* Economic inequality, difference in economic well-being between population groups
* ...
are also true in any ordered ring
In abstract algebra, an ordered ring is a (usually commutative) ring ''R'' with a total order ≤ such that for all ''a'', ''b'', and ''c'' in ''R'':
* if ''a'' ≤ ''b'' then ''a'' + ''c'' ≤ ''b'' + ''c''.
* if 0 ≤ ''a'' and 0 ≤ ''b'' the ...
.
Volumes of similar Euclidean solids
Solid is one of the four fundamental states of matter (the others being liquid, gas, and plasma). The molecules in a solid are closely packed together and contain the least amount of kinetic energy. A solid is characterized by structural ...
are related as cubes of their linear sizes.
In complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s, the cube of a purely imaginary number is also purely imaginary. For example, .
The derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
of equals .
Cubes ''occasionally'' have the surjective property in other fields
Fields may refer to:
Music
*Fields (band), an indie rock band formed in 2006
*Fields (progressive rock band), a progressive rock band formed in 1971
* ''Fields'' (album), an LP by Swedish-based indie rock band Junip (2010)
* "Fields", a song by ...
, such as in for such prime that , but not necessarily: see the counterexample with rationals above. Also in only three elements 0, ±1 are perfect cubes, of seven total. −1, 0, and 1 are perfect cubes ''anywhere'' and the only elements of a field equal to the own cubes: .
History
Determination of the cubes of large numbers was very common in many ancient civilizations. Mesopotamian mathematicians created cuneiform tablets with tables for calculating cubes and cube roots by theOld Babylonian
Old Babylonian may refer to:
*the period of the First Babylonian dynasty (20th to 16th centuries BC)
*the historical stage of the Akkadian language
Akkadian (, Akkadian: )John Huehnergard & Christopher Woods, "Akkadian and Eblaite", ''The Camb ...
period (20th to 16th centuries BC). Cubic equations were known to the ancient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic peri ...
mathematician Diophantus
Diophantus of Alexandria ( grc, Διόφαντος ὁ Ἀλεξανδρεύς; born probably sometime between AD 200 and 214; died around the age of 84, probably sometime between AD 284 and 298) was an Alexandrian mathematician, who was the aut ...
. Hero of Alexandria
Hero of Alexandria (; grc-gre, Ἥρων ὁ Ἀλεξανδρεύς, ''Heron ho Alexandreus'', also known as Heron of Alexandria ; 60 AD) was a Greece, Greek mathematician and engineer who was active in his native city of Alexandria, Roman Egy ...
devised a method for calculating cube roots in the 1st century CE. Methods for solving cubic equations and extracting cube roots appear in ''The Nine Chapters on the Mathematical Art
''The Nine Chapters on the Mathematical Art'' () is a Chinese mathematics book, composed by several generations of scholars from the 10th–2nd century BCE, its latest stage being from the 2nd century CE. This book is one of the earliest sur ...
'', a Chinese mathematical text compiled around the 2nd century BCE and commented on by Liu Hui
Liu Hui () was a Chinese mathematician who published a commentary in 263 CE on ''Jiu Zhang Suan Shu (The Nine Chapters on the Mathematical Art).'' He was a descendant of the Marquis of Zixiang of the Eastern Han dynasty and lived in the state o ...
in the 3rd century CE.
See also
*Cabtaxi number In mathematics, the ''n''-th cabtaxi number, typically denoted Cabtaxi(''n''), is defined as the smallest positive integer that can be written as the sum of two ''positive or negative or 0'' cubes in ''n'' ways. Such numbers exist for all ''n'', whi ...
* Cubic equation
In algebra, a cubic equation in one variable is an equation of the form
:ax^3+bx^2+cx+d=0
in which is nonzero.
The solutions of this equation are called roots of the cubic function defined by the left-hand side of the equation. If all of the ...
* Doubling the cube
Doubling the cube, also known as the Delian problem, is an ancient geometric problem. Given the edge of a cube, the problem requires the construction of the edge of a second cube whose volume is double that of the first. As with the related pro ...
* Eighth power
In arithmetic and algebra the eighth power of a number ''n'' is the result of multiplying eight instances of ''n'' together. So:
:.
Eighth powers are also formed by multiplying a number by its seventh power, or the fourth power of a number by it ...
* Euler's sum of powers conjecture
Euler's conjecture is a disproved conjecture in mathematics related to Fermat's Last Theorem. It was proposed by Leonhard Euler in 1769. It states that for all integers and greater than 1, if the sum of many th powers of positive integers is ...
* Fifth power
* Fourth power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So:
:''n''4 = ''n'' × ''n'' × ''n'' × ''n''
Fourth powers are also formed by multiplying a number by its cube. Further ...
* Kepler's laws of planetary motion#Third law
* Monkey saddle
In mathematics, the monkey saddle is the surface defined by the equation
: z = x^3 - 3xy^2, \,
or in cylindrical coordinates
:z = \rho^3 \cos(3\varphi).
It belongs to the class of saddle surfaces, and its name derives from the observation tha ...
* Perfect power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' ...
* Seventh power
In arithmetic and algebra the seventh power of a number ''n'' is the result of multiplying seven instances of ''n'' together. So:
:.
Seventh powers are also formed by multiplying a number by its sixth power, the square of a number by its fifth p ...
* Sixth power In arithmetic and algebra the sixth power of a number ''n'' is the result of multiplying six instances of ''n'' together. So:
:.
Sixth powers can be formed by multiplying a number by its fifth power, multiplying the square of a number by its fourt ...
* Square
In Euclidean geometry, a square is a regular quadrilateral, which means that it has four equal sides and four equal angles (90-degree angles, π/2 radian angles, or right angles). It can also be defined as a rectangle with two equal-length adj ...
* Taxicab number
In mathematics, the ''n''th taxicab number, typically denoted Ta(''n'') or Taxicab(''n''), also called the ''n''th Hardy–Ramanujan number, is defined as the smallest integer that can be expressed as a sum of two ''positive'' integer cubes in ...
References
Sources
* * * * * * * * {{Series_(mathematics) Elementary arithmetic Figurate numbers Integer sequences Integers Number theory Unary operations