|
Fifth Power (algebra)
In arithmetic and algebra, the fifth power or sursolid of a number ''n'' is the result of multiplying five instances of ''n'' together: :. Fifth powers are also formed by multiplying a number by its fourth power, or the square of a number by its cube. The sequence of fifth powers of integers is: :0, 1, 32, 243, 1024, 3125, 7776, 16807, 32768, 59049, 100000, 161051, 248832, 371293, 537824, 759375, 1048576, 1419857, 1889568, 2476099, 3200000, 4084101, 5153632, 6436343, 7962624, 9765625, ... Properties For any integer ''n'', the last decimal digit of ''n''5 is the same as the last (decimal) digit of ''n''. I.E: : n \equiv n^5\pmod By the Abel–Ruffini theorem, there is no general algebraic formula (formula expressed in terms of radical expressions) for the solution of polynomial equations containing a fifth power of the unknown as their highest power. This is the lowest power for which this is true. See quintic equation, sextic equation, and septic equation. Along with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers— addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th century, Italian mathematician Giuseppe Peano formalized arithmetic with his Peano axioms, which are highly important to the field of mathematical logic today. History The prehistory of arithmetic is limited to a small number of artifacts, which may indicate the conception of addition and subtraction, the best-known being the Ishango bone from central Africa, dating from somewhere between 20,000 and 18,000 BC, although its interpretation is disputed. The earliest written records indicate the Egyptians and Babylonians used all the elementary arithmetic operations: addition, subtraction, multiplication, and division, as early as 2000 BC. These artifacts do not always reveal the specific process used for solving problems, but t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Septic Equation
In algebra, a septic equation is an equation of the form :ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h=0,\, where . A septic function is a function of the form :f(x)=ax^7+bx^6+cx^5+dx^4+ex^3+fx^2+gx+h\, where . In other words, it is a polynomial of degree seven. If , then ''f'' is a sextic function (), quintic function (), etc. The equation may be obtained from the function by setting . The ''coefficients'' may be either integers, rational numbers, real numbers, complex numbers or, more generally, members of any field. Because they have an odd degree, septic functions appear similar to quintic or cubic function when graphed, except they may possess additional local maxima and local minima (up to three maxima and three minima). The derivative of a septic function is a sextic function. Solvable septics Some seventh degree equations can be solved by factorizing into radicals, but other septics cannot. Évariste Galois developed techniques for determining whether a given equation cou ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integer Sequences
In mathematics, an integer sequence is a sequence (i.e., an ordered list) of integers. An integer sequence may be specified ''explicitly'' by giving a formula for its ''n''th term, or ''implicitly'' by giving a relationship between its terms. For example, the sequence 0, 1, 1, 2, 3, 5, 8, 13, ... (the Fibonacci sequence) is formed by starting with 0 and 1 and then adding any two consecutive terms to obtain the next one: an implicit description. The sequence 0, 3, 8, 15, ... is formed according to the formula ''n''2 − 1 for the ''n''th term: an explicit definition. Alternatively, an integer sequence may be defined by a property which members of the sequence possess and other integers do not possess. For example, we can determine whether a given integer is a perfect number, even though we do not have a formula for the ''n''th perfect number. Examples Integer sequences that have their own name include: *Abundant numbers *Baum–Sweet sequence *Bell numbe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Elementary Arithmetic
The operators in elementary arithmetic are addition, subtraction, multiplication, and division. The operators can be applied on both real numbers and imaginary numbers. Each kind of number is represented on a number line designated to the type. Digits Digits are the set of symbols used to represent numbers. In a numeral system, each digit represents a value. The Arabic numerals (0, 1, 2, 3, 4, 5, 6, 7, 8, 9) are the most common set of symbols, and the most frequently used form of these digits is the Western style. A numeral system defines the value of all numbers that contain more than one digit, most often by adding the value of adjacent digits. The Hindu–Arabic numeral system includes positional notation to determine the value of any numeral. In this type of system, the increase in value of an additional digit includes one or more multiplications with the radix value and the result is added to the value of an adjacent digit. For example, with Arabic numerals, the radix ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Number Theory
Number theory (or arithmetic or higher arithmetic in older usage) is a branch of pure mathematics devoted primarily to the study of the integers and arithmetic function, integer-valued functions. German mathematician Carl Friedrich Gauss (1777–1855) said, "Mathematics is the queen of the sciences—and number theory is the queen of mathematics."German original: "Die Mathematik ist die Königin der Wissenschaften, und die Arithmetik ist die Königin der Mathematik." Number theorists study prime numbers as well as the properties of mathematical objects made out of integers (for example, rational numbers) or defined as generalizations of the integers (for example, algebraic integers). Integers can be considered either in themselves or as solutions to equations (Diophantine geometry). Questions in number theory are often best understood through the study of Complex analysis, analytical objects (for example, the Riemann zeta function) that encode properties of the integers, primes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Integers
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language of mathematics, the set of integers is often denoted by the boldface or blackboard bold \mathbb. The set of natural numbers \mathbb is a subset of \mathbb, which in turn is a subset of the set of all rational numbers \mathbb, itself a subset of the real numbers \mathbb. Like the natural numbers, \mathbb is Countable set, countably infinite. An integer may be regarded as a real number that can be written without a fraction, fractional component. For example, 21, 4, 0, and −2048 are integers, while 9.75, , and are not. The integers form the smallest Group (mathematics), group and the smallest ring (mathematics), ring containing the natural numbers. In algebraic number theory, the integers are sometimes qualified as rational integers ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
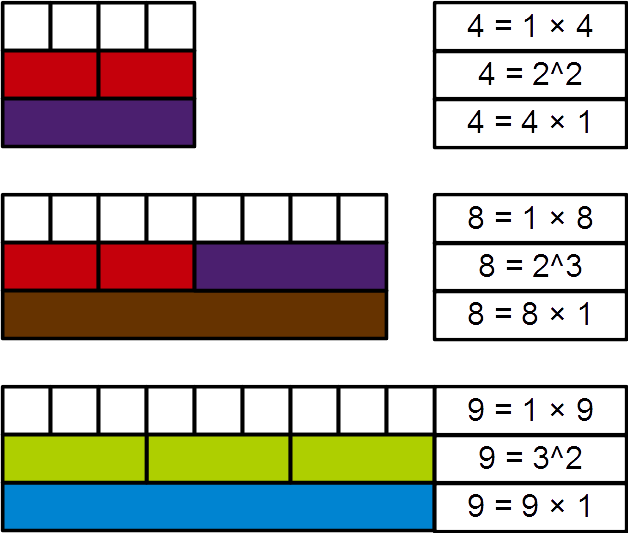
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Square (algebra)
In mathematics, a square is the result of multiplication, multiplying a number by itself. The verb "to square" is used to denote this operation. Squaring is the same as exponentiation, raising to the power 2 (number), 2, and is denoted by a superscript 2; for instance, the square of 3 may be written as 32, which is the number 9. In some cases when superscripts are not available, as for instance in programming languages or plain text files, the notations ''x''^2 (caret) or ''x''**2 may be used in place of ''x''2. The adjective which corresponds to squaring is ''wikt:quadratic, quadratic''. The square of an integer may also be called a square number or a perfect square. In algebra, the operation of squaring is often generalized to polynomials, other expression (mathematics), expressions, or values in systems of mathematical values other than the numbers. For instance, the square of the linear function (calculus), linear polynomial is the quadratic polynomial . One of the imp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (algebra)
In arithmetic and algebra, the cube of a number is its third power, that is, the result of multiplying three instances of together. The cube of a number or any other mathematical expression is denoted by a superscript 3, for example or . The cube is also the number multiplied by its square: :. The ''cube function'' is the function (often denoted ) that maps a number to its cube. It is an odd function, as :. The volume of a geometric cube is the cube of its side length, giving rise to the name. The inverse operation that consists of finding a number whose cube is is called extracting the cube root of . It determines the side of the cube of a given volume. It is also raised to the one-third power. The graph of the cube function is known as the cubic parabola. Because the cube function is an odd function, this curve has a center of symmetry at the origin, but no axis of symmetry. In integers A cube number, or a perfect cube, or sometimes just a cube, is a number wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourth Power
In arithmetic and algebra, the fourth power of a number ''n'' is the result of multiplying four instances of ''n'' together. So: :''n''4 = ''n'' × ''n'' × ''n'' × ''n'' Fourth powers are also formed by multiplying a number by its cube. Furthermore, they are squares of squares. The sequence of fourth powers of integers (also known as biquadrates or tesseractic numbers) is: :0, 1, 16, 81, 256, 625, 1296, 2401, 4096, 6561, 10000, 14641, 20736, 28561, 38416, 50625, 65536, 83521, 104976, 130321, 160000, 194481, 234256, 279841, 331776, 390625, 456976, 531441, 614656, 707281, 810000, ... . Properties The last digit of a fourth power in decimal can only be 0 (in fact 0000), 1, 5 (in fact 0625), or 6. Every positive integer can be expressed as the sum of at most 19 fourth powers; every integer larger than 13792 can be expressed as the sum of at most 16 fourth powers (see Waring's problem). Fermat knew that a fourth power cannot be the sum of two other fourth powers (the ''n'' = 4 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sixth Power
In arithmetic and algebra the sixth power of a number ''n'' is the result of multiplying six instances of ''n'' together. So: :. Sixth powers can be formed by multiplying a number by its fifth power, multiplying the square of a number by its fourth power, by cubing a square, or by squaring a cube. The sequence of sixth powers of integers is: :0, 1, 64, 729, 4096, 15625, 46656, 117649, 262144, 531441, 1000000, 1771561, 2985984, 4826809, 7529536, 11390625, 16777216, 24137569, 34012224, 47045881, 64000000, 85766121, 113379904, 148035889, 191102976, 244140625, 308915776, 387420489, 481890304, ... They include the significant decimal numbers 106 (a million), 1006 (a short-scale trillion and long-scale billion), 10006 (a long-scale trillion) and so on. Squares and cubes The sixth powers of integers can be characterized as the numbers that are simultaneously squares and cubes. In this way, they are analogous to two other classes of figurate numbers: the square triangular numbers, w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Seventh Power
In arithmetic and algebra the seventh power of a number ''n'' is the result of multiplying seven instances of ''n'' together. So: :. Seventh powers are also formed by multiplying a number by its sixth power, the square of a number by its fifth power, or the cube of a number by its fourth power. The sequence of seventh powers of integers is: :0, 1, 128, 2187, 16384, 78125, 279936, 823543, 2097152, 4782969, 10000000, 19487171, 35831808, 62748517, 105413504, 170859375, 268435456, 410338673, 612220032, 893871739, 1280000000, 1801088541, 2494357888, 3404825447, 4586471424, 6103515625, 8031810176, ... In the archaic notation of Robert Recorde, the seventh power of a number was called the "second sursolid". Properties Leonard Eugene Dickson studied generalizations of Waring's problem for seventh powers, showing that every non-negative integer can be represented as a sum of at most 258 non-negative seventh powers (17 is 1, and 27 is 128). All but finitely many positive integers ca ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |