cotangent on:
[Wikipedia]
[Google]
[Amazon]
 In
In

 If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the
If the acute angle is given, then any right triangles that have an angle of are similar to each other. This means that the ratio of any two side lengths depends only on . Thus these six ratios define six functions of , which are the trigonometric functions. In the following definitions, the 
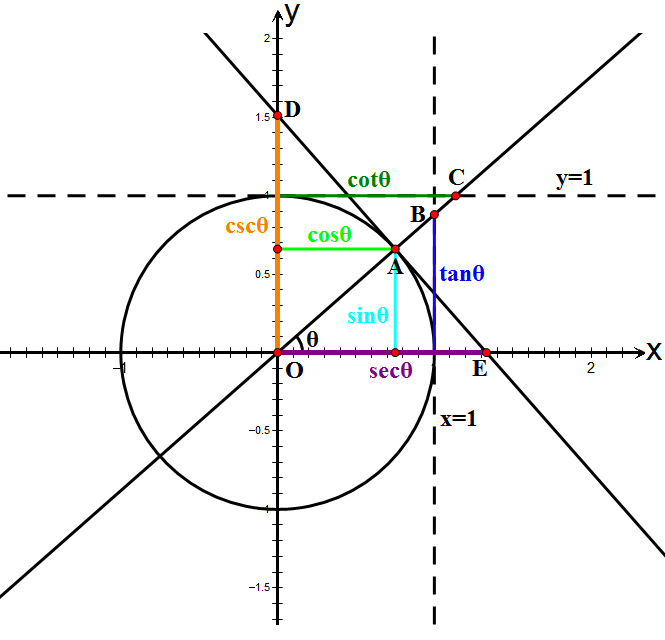 The six trigonometric functions can be defined as coordinate values of points on the
The six trigonometric functions can be defined as coordinate values of points on the  Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
Since a rotation of an angle of does not change the position or size of a shape, the points , , , , and are the same for two angles whose difference is an integer multiple of . Thus trigonometric functions are
 The
The

 The modern trend in mathematics is to build
The modern trend in mathematics is to build



 The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe
The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe
mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics ...
, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real function
In mathematical analysis, and applications in geometry, applied mathematics, engineering, and natural sciences, a function of a real variable is a function whose domain is the real numbers \mathbb, or a subset of \mathbb that contains an interv ...
s which relate an angle of a right-angled triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right an ...
to ratios of two side lengths. They are widely used in all sciences that are related to geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, such as navigation
Navigation is a field of study that focuses on the process of monitoring and controlling the movement of a craft or vehicle from one place to another.Bowditch, 2003:799. The field of navigation includes four general categories: land navigation, ...
, solid mechanics
Solid mechanics, also known as mechanics of solids, is the branch of continuum mechanics that studies the behavior of solid materials, especially their motion and deformation under the action of forces, temperature changes, phase changes, and ot ...
, celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of objects in outer space. Historically, celestial mechanics applies principles of physics (classical mechanics) to astronomical objects, such as stars and planets, to ...
, geodesy
Geodesy ( ) is the Earth science of accurately measuring and understanding Earth's figure (geometric shape and size), orientation in space, and gravity. The field also incorporates studies of how these properties change over time and equivale ...
, and many others. They are among the simplest periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
s, and as such are also widely used for studying periodic phenomena through Fourier analysis
In mathematics, Fourier analysis () is the study of the way general functions may be represented or approximated by sums of simpler trigonometric functions. Fourier analysis grew from the study of Fourier series, and is named after Josep ...
.
The trigonometric functions most widely used in modern mathematics are the sine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is oppo ...
, the cosine, and the tangent. Their reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
s are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon X\t ...
, and an analog among the hyperbolic functions
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the un ...
.
The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ar ...
s. To extend the sine and cosine functions to functions whose domain
Domain may refer to:
Mathematics
*Domain of a function, the set of input values for which the (total) function is defined
**Domain of definition of a partial function
**Natural domain of a partial function
**Domain of holomorphy of a function
* Do ...
is the whole real line
In elementary mathematics, a number line is a picture of a graduated straight line (geometry), line that serves as visual representation of the real numbers. Every point of a number line is assumed to correspond to a real number, and every real ...
, geometrical definitions using the standard unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucl ...
(i.e., a circle with radius
In classical geometry, a radius ( : radii) of a circle or sphere is any of the line segments from its center to its perimeter, and in more modern usage, it is also their length. The name comes from the latin ''radius'', meaning ray but also the ...
1 unit) are often used; then the domain of the other functions is the real line with some isolated points removed. Modern definitions express trigonometric functions as infinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
or as solutions of differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
s. This allows extending the domain of sine and cosine functions to the whole complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the ...
, and the domain of the other trigonometric functions to the complex plane with some isolated points removed.
Notation
Conventionally, an abbreviation of each trigonometric function's name is used as its symbol in formulas. Today, the most common versions of these abbreviations are "sin" for sine, "cos" for cosine, "tan" or "tg" for tangent, "sec" for secant, "csc" or "cosec" for cosecant, and "cot" or "ctg" for cotangent. Historically, these abbreviations were first used in prose sentences to indicate particularline segment
In geometry, a line segment is a part of a straight line that is bounded by two distinct end points, and contains every point on the line that is between its endpoints. The length of a line segment is given by the Euclidean distance between ...
s or their lengths related to an arc of an arbitrary circle, and later to indicate ratios of lengths, but as the function concept developed in the 17th–18th century, they began to be considered as functions of real-number-valued angle measures, and written with functional notation
In mathematics, a function from a set to a set assigns to each element of exactly one element of .; the words map, mapping, transformation, correspondence, and operator are often used synonymously. The set is called the domain of the functi ...
, for example . Parentheses are still often omitted to reduce clutter, but are sometimes necessary; for example the expression would typically be interpreted to mean so parentheses are required to express
A positive integer
In mathematics, the natural numbers are those numbers used for counting (as in "there are ''six'' coins on the table") and ordering (as in "this is the ''third'' largest city in the country").
Numbers used for counting are called ''cardinal n ...
appearing as a superscript after the symbol of the function denotes exponentiation
Exponentiation is a mathematical operation, written as , involving two numbers, the '' base'' and the ''exponent'' or ''power'' , and pronounced as " (raised) to the (power of) ". When is a positive integer, exponentiation corresponds to re ...
, not function composition
In mathematics, function composition is an operation that takes two functions and , and produces a function such that . In this operation, the function is applied to the result of applying the function to . That is, the functions and ...
. For example and denote not This differs from the (historically later) general functional notation in which
However, the exponent is commonly used to denote the inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon X\t ...
, not the reciprocal
Reciprocal may refer to:
In mathematics
* Multiplicative inverse, in mathematics, the number 1/''x'', which multiplied by ''x'' gives the product 1, also known as a ''reciprocal''
* Reciprocal polynomial, a polynomial obtained from another pol ...
. For example and denote the inverse trigonometric function
In mathematics, the inverse trigonometric functions (occasionally also called arcus functions, antitrigonometric functions or cyclometric functions) are the inverse functions of the trigonometric functions (with suitably restricted domains). Spec ...
alternatively written The equation implies not In this case, the superscript ''could'' be considered as denoting a composed or iterated function
In mathematics, an iterated function is a function (that is, a function from some set to itself) which is obtained by composing another function with itself a certain number of times. The process of repeatedly applying the same function is ...
, but negative superscripts other than are not in common use.
Right-angled triangle definitions
hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equa ...
is the length of the side opposite the right angle, ''opposite'' represents the side opposite the given angle , and ''adjacent'' represents the side between the angle and the right angle.
In a right-angled triangle, the sum of the two acute angles is a right angle, that is, or . Therefore and represent the same ratio, and thus are equal. This identity and analogous relationships between the other trigonometric functions are summarized in the following table.
Radians versus degrees
In geometric applications, the argument of a trigonometric function is generally the measure of anangle
In Euclidean geometry, an angle is the figure formed by two Ray (geometry), rays, called the ''Side (plane geometry), sides'' of the angle, sharing a common endpoint, called the ''vertex (geometry), vertex'' of the angle.
Angles formed by two ...
. For this purpose, any angular unit
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles a ...
is convenient, and angles are most commonly measured in conventional units of degrees in which a right angle is 90° and a complete turn is 360° (particularly in elementary mathematics
Elementary mathematics consists of mathematics topics frequently taught at the primary or secondary school levels.
In the Canadian curriculum, there are six basic strands in Elementary Mathematics: Number, Algebra, Data, Spatial Sense, Finan ...
).
However, in calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
and mathematical analysis
Analysis is the branch of mathematics dealing with continuous functions, limit (mathematics), limits, and related theories, such as Derivative, differentiation, Integral, integration, measure (mathematics), measure, infinite sequences, series (m ...
, the trigonometric functions are generally regarded more abstractly as functions of real
Real may refer to:
Currencies
* Brazilian real (R$)
* Central American Republic real
* Mexican real
* Portuguese real
* Spanish real
* Spanish colonial real
Music Albums
* ''Real'' (L'Arc-en-Ciel album) (2000)
* ''Real'' (Bright album) (2010) ...
or complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
s, rather than angles. In fact, the functions sin and cos can be defined for all complex numbers in terms of the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, a ...
via power series or as solutions to differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
s given particular initial values (''see below''), without reference to any geometric notions. The other four trigonometric functions (tan, cot, sec, csc) can be defined as quotients and reciprocals of sin and cos, except where zero occurs in the denominator. It can be proved, for real arguments, that these definitions coincide with elementary geometric definitions ''if'' ''the argument is regarded as an angle given in radians''. Moreover, these definitions result in simple expressions for the derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
s and indefinite integrals for the trigonometric functions. Thus, in settings beyond elementary geometry, radians are regarded as the mathematically natural unit for describing angle measures.
When radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that c ...
s (rad) are employed, the angle is given as the length of the arc of the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucl ...
subtended by it: the angle that subtends an arc of length 1 on the unit circle is 1 rad (≈ 57.3°), and a complete turn (360°) is an angle of 2 (≈ 6.28) rad. For real number ''x'', the notations sin ''x'', cos ''x'', etc. refer to the value of the trigonometric functions evaluated at an angle of ''x'' rad. If units of degrees are intended, the degree sign must be explicitly shown (e.g., sin ''x°'', cos ''x°'', etc.). Using this standard notation, the argument ''x'' for the trigonometric functions satisfies the relationship ''x'' = (180''x''/)°, so that, for example, sin = sin 180° when we take ''x'' = . In this way, the degree symbol can be regarded as a mathematical constant such that 1° = /180 ≈ 0.0175.
Unit-circle definitions
 The six trigonometric functions can be defined as coordinate values of points on the
The six trigonometric functions can be defined as coordinate values of points on the Euclidean plane
In mathematics, the Euclidean plane is a Euclidean space of dimension two. That is, a geometric setting in which two real quantities are required to determine the position of each point ( element of the plane), which includes affine notions of ...
that are related to the unit circle
In mathematics, a unit circle is a circle of unit radius—that is, a radius of 1. Frequently, especially in trigonometry, the unit circle is the circle of radius 1 centered at the origin (0, 0) in the Cartesian coordinate system in the Eucl ...
, which is the circle
A circle is a shape consisting of all points in a plane that are at a given distance from a given point, the centre. Equivalently, it is the curve traced out by a point that moves in a plane so that its distance from a given point is const ...
of radius one centered at the origin of this coordinate system. While right-angled triangle definitions allow for the definition of the trigonometric functions for angles between and radian
The radian, denoted by the symbol rad, is the unit of angle in the International System of Units (SI) and is the standard unit of angular measure used in many areas of mathematics. The unit was formerly an SI supplementary unit (before that c ...
s the unit circle definitions allow the domain of trigonometric functions to be extended to all positive and negative real numbers.
Let be the ray obtained by rotating by an angle the positive half of the -axis (counterclockwise
Two-dimensional rotation can occur in two possible directions. Clockwise motion (abbreviated CW) proceeds in the same direction as a clock's hands: from the top to the right, then down and then to the left, and back up to the top. The opposite ...
rotation for and clockwise rotation for ). This ray intersects the unit circle at the point The ray extended to a line if necessary, intersects the line of equation at point and the line of equation at point The tangent line
In geometry, the tangent line (or simply tangent) to a plane curve at a given point is the straight line that "just touches" the curve at that point. Leibniz defined it as the line through a pair of infinitely close points on the curve. More ...
to the unit circle at the point , is perpendicular
In elementary geometry, two geometric objects are perpendicular if they intersect at a right angle (90 degrees or π/2 radians). The condition of perpendicularity may be represented graphically using the ''perpendicular symbol'', ⟂. It can ...
to and intersects the - and -axes at points and The coordinates
In geometry, a coordinate system is a system that uses one or more numbers, or coordinates, to uniquely determine the position of the points or other geometric elements on a manifold such as Euclidean space. The order of the coordinates is sig ...
of these points give the values of all trigonometric functions for any arbitrary real value of in the following manner.
The trigonometric functions and are defined, respectively, as the ''x''- and ''y''-coordinate values of point . That is,
: and
In the range , this definition coincides with the right-angled triangle definition, by taking the right-angled triangle to have the unit radius as hypotenuse
In geometry, a hypotenuse is the longest side of a right-angled triangle, the side opposite the right angle. The length of the hypotenuse can be found using the Pythagorean theorem, which states that the square of the length of the hypotenuse equa ...
. And since the equation holds for all points on the unit circle, this definition of cosine and sine also satisfies the Pythagorean identity
The Pythagorean trigonometric identity, also called simply the Pythagorean identity, is an identity expressing the Pythagorean theorem in terms of trigonometric functions. Along with the sum-of-angles formulae, it is one of the basic relations be ...
.
:
The other trigonometric functions can be found along the unit circle as
: and
: and
By applying the Pythagorean identity and geometric proof methods, these definitions can readily be shown to coincide with the definitions of tangent, cotangent, secant and cosecant in terms of sine and cosine, that is
:
periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
s with period . That is, the equalities
: and
hold for any angle and any integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign (−1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
. The same is true for the four other trigonometric functions. By observing the sign and the monotonicity of the functions sine, cosine, cosecant, and secant in the four quadrants, one can show that is the smallest value for which they are periodic (i.e., is the fundamental period of these functions). However, after a rotation by an angle , the points and already return to their original position, so that the tangent function and the cotangent function have a fundamental period of . That is, the equalities
: and
hold for any angle and any integer .
Algebraic values
algebraic expression In mathematics, an algebraic expression is an expression built up from integer constants, variables, and the algebraic operations (addition, subtraction, multiplication, division and exponentiation by an exponent that is a rational number). For ex ...
s for the most important angles are as follows:
: ( zero angle)
:
:
:
: (right angle
In geometry and trigonometry, a right angle is an angle of exactly 90 Degree (angle), degrees or radians corresponding to a quarter turn (geometry), turn. If a Line (mathematics)#Ray, ray is placed so that its endpoint is on a line and the ad ...
)
Writing the numerators as square roots
In mathematics, a square root of a number is a number such that ; in other words, a number whose ''square'' (the result of multiplying the number by itself, or ⋅ ) is . For example, 4 and −4 are square roots of 16, because .
E ...
of consecutive non-negative integers, with a denominator of 2, provides an easy way to remember the values.
Such simple expressions generally do not exist for other angles which are rational multiples of a right angle.
*For an angle which, measured in degrees, is a multiple of three, the exact trigonometric values
In mathematics, the values of the trigonometric functions can be expressed approximately, as in \cos (\pi/4) \approx 0.707, or exactly, as in \cos (\pi/ 4)= \sqrt 2 /2. While trigonometric tables contain many approximate values, the exact values f ...
of the sine and the cosine may be expressed in terms of square roots. These values of the sine and the cosine may thus be constructed by ruler and compass
In geometry, straightedge-and-compass construction – also known as ruler-and-compass construction, Euclidean construction, or classical construction – is the construction of lengths, angles, and other geometric figures using only an ideali ...
.
*For an angle of an integer number of degrees, the sine and the cosine may be expressed in terms of square roots and the cube root
In mathematics, a cube root of a number is a number such that . All nonzero real numbers, have exactly one real cube root and a pair of complex conjugate cube roots, and all nonzero complex numbers have three distinct complex cube roots. Fo ...
of a non-real complex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
. Galois theory
In mathematics, Galois theory, originally introduced by Évariste Galois, provides a connection between field theory and group theory. This connection, the fundamental theorem of Galois theory, allows reducing certain problems in field theory to ...
allows a proof that, if the angle is not a multiple of 3°, non-real cube roots are unavoidable.
*For an angle which, expressed in degrees, is a rational number
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all ration ...
, the sine and the cosine are algebraic number
An algebraic number is a number that is a root of a non-zero polynomial in one variable with integer (or, equivalently, rational) coefficients. For example, the golden ratio, (1 + \sqrt)/2, is an algebraic number, because it is a root of the po ...
s, which may be expressed in terms of th roots. This results from the fact that the Galois group
In mathematics, in the area of abstract algebra known as Galois theory, the Galois group of a certain type of field extension is a specific group associated with the field extension. The study of field extensions and their relationship to the pol ...
s of the cyclotomic polynomial
In mathematics, the ''n''th cyclotomic polynomial, for any positive integer ''n'', is the unique irreducible polynomial with integer coefficients that is a divisor of x^n-1 and is not a divisor of x^k-1 for any Its roots are all ''n''th primiti ...
s are cyclic
Cycle, cycles, or cyclic may refer to:
Anthropology and social sciences
* Cyclic history, a theory of history
* Cyclical theory, a theory of American political history associated with Arthur Schlesinger, Sr.
* Social cycle, various cycles in s ...
.
*For an angle which, expressed in degrees, is not a rational number, then either the angle or both the sine and the cosine are transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, not the root of a non-zero polynomial of finite degree with rational coefficients. The best known transcendental numbers are and .
Though only a few classes ...
s. This is a corollary of Baker's theorem
In transcendental number theory, a mathematical discipline, Baker's theorem gives a lower bound for the absolute value of linear combinations of logarithms of algebraic numbers. The result, proved by , subsumed many earlier results in transcendent ...
, proved in 1966.
Simple algebraic values
The following table lists the sines, cosines, and tangents of multiples of 15 degrees from 0 to 90 degrees.In calculus
Graphs of sine, cosine and tangentgeometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
from calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
rather than the converse. Therefore, except at a very elementary level, trigonometric functions are defined using the methods of calculus.
Trigonometric functions are differentiable
In mathematics, a differentiable function of one real variable is a function whose derivative exists at each point in its domain. In other words, the graph of a differentiable function has a non-vertical tangent line at each interior point in its ...
and analytic at every point where they are defined; that is, everywhere for the sine and the cosine, and, for the tangent, everywhere except at for every integer .
The trigonometric function are periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
s, and their primitive period is for the sine and the cosine, and for the tangent, which is increasing
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
in each open interval
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other ...
. At each end point of these intervals, the tangent function has a vertical asymptote
In analytic geometry, an asymptote () of a curve is a line such that the distance between the curve and the line approaches zero as one or both of the ''x'' or ''y'' coordinates tends to infinity. In projective geometry and related context ...
.
In calculus, there are two equivalent definitions of trigonometric functions, either using power series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a const ...
or differential equation
In mathematics, a differential equation is an equation that relates one or more unknown functions and their derivatives. In applications, the functions generally represent physical quantities, the derivatives represent their rates of change, an ...
s. These definitions are equivalent, as starting from one of them, it is easy to retrieve the other as a property. However the definition through differential equations is somehow more natural, since, for example, the choice of the coefficients of the power series may appear as quite arbitrary, and the Pythagorean identity is much easier to deduce from the differential equations.
Definition by differential equations
Sine and cosine can be defined as the unique solution to theinitial value problem
In multivariable calculus, an initial value problem (IVP) is an ordinary differential equation together with an initial condition which specifies the value of the unknown function at a given point in the domain. Modeling a system in physics or oth ...
:
:
Differentiating again, and , so both sine and cosine are solutions of the ordinary differential equation
In mathematics, an ordinary differential equation (ODE) is a differential equation whose unknown(s) consists of one (or more) function(s) of one variable and involves the derivatives of those functions. The term ''ordinary'' is used in contrast w ...
:
Applying the quotient rule
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h(x)=f(x)/g(x), where both and are differentiable and g(x)\neq 0. The quotient rule states that the deriva ...
to the tangent , we derive
:
Power series expansion
Applying the differential equations topower series
In mathematics, a power series (in one variable) is an infinite series of the form
\sum_^\infty a_n \left(x - c\right)^n = a_0 + a_1 (x - c) + a_2 (x - c)^2 + \dots
where ''an'' represents the coefficient of the ''n''th term and ''c'' is a const ...
with indeterminate coefficients, one may deduce recurrence relation
In mathematics, a recurrence relation is an equation according to which the nth term of a sequence of numbers is equal to some combination of the previous terms. Often, only k previous terms of the sequence appear in the equation, for a parameter ...
s for the coefficients of the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor serie ...
of the sine and cosine functions. These recurrence relations are easy to solve, and give the series expansions
:
The radius of convergence
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or \infty. When it is positive, the power series co ...
of these series is infinite. Therefore, the sine and the cosine can be extended to entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic on the whole complex plane. Typical examples of entire functions are polynomials and the exponential function, and any fin ...
s (also called "sine" and "cosine"), which are (by definition) complex-valued function
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is helpful in many branches of mathematics, including algebraic ...
s that are defined and holomorphic
In mathematics, a holomorphic function is a complex-valued function of one or more complex variables that is complex differentiable in a neighbourhood of each point in a domain in complex coordinate space . The existence of a complex derivati ...
on the whole complex plane
In mathematics, the complex plane is the plane formed by the complex numbers, with a Cartesian coordinate system such that the -axis, called the real axis, is formed by the real numbers, and the -axis, called the imaginary axis, is formed by the ...
.
Being defined as fractions of entire functions, the other trigonometric functions may be extended to meromorphic function
In the mathematical field of complex analysis, a meromorphic function on an open subset ''D'' of the complex plane is a function that is holomorphic on all of ''D'' ''except'' for a set of isolated points, which are pole (complex analysis), pole ...
s, that is functions that are holomorphic in the whole complex plane, except some isolated points called poles
Poles,, ; singular masculine: ''Polak'', singular feminine: ''Polka'' or Polish people, are a West Slavic nation and ethnic group, who share a common history, culture, the Polish language and are identified with the country of Poland in Ce ...
. Here, the poles are the numbers of the form for the tangent and the secant, or for the cotangent and the cosecant, where is an arbitrary integer.
Recurrences relations may also be computed for the coefficients of the Taylor series
In mathematics, the Taylor series or Taylor expansion of a function is an infinite sum of terms that are expressed in terms of the function's derivatives at a single point. For most common functions, the function and the sum of its Taylor serie ...
of the other trigonometric functions. These series have a finite radius of convergence
In mathematics, the radius of convergence of a power series is the radius of the largest disk at the center of the series in which the series converges. It is either a non-negative real number or \infty. When it is positive, the power series co ...
. Their coefficients have a combinatorial
Combinatorics is an area of mathematics primarily concerned with counting, both as a means and an end in obtaining results, and certain properties of finite structures. It is closely related to many other areas of mathematics and has many ap ...
interpretation: they enumerate alternating permutation
In combinatorial mathematics, an alternating permutation (or zigzag permutation) of the set is a permutation (arrangement) of those numbers so that each entry is alternately greater or less than the preceding entry. For example, the five alte ...
s of finite sets.
More precisely, defining
: , the th up/down number,
: , the th Bernoulli number
In mathematics, the Bernoulli numbers are a sequence of rational numbers which occur frequently in analysis. The Bernoulli numbers appear in (and can be defined by) the Taylor series expansions of the tangent and hyperbolic tangent functions, ...
, and
: , is the th Euler number
In mathematics, the Euler numbers are a sequence ''En'' of integers defined by the Taylor series expansion
:\frac = \frac = \sum_^\infty \frac \cdot t^n,
where \cosh (t) is the hyperbolic cosine function. The Euler numbers are related to a ...
,
one has the following series expansions:
:
:
:
:
Continued fraction expansion
The following expansions are valid in the whole complex plane: : : : The last one was used in the historically firstproof that π is irrational
In the 1760s, Johann Heinrich Lambert was the first to prove that the number is irrational, meaning it cannot be expressed as a fraction a/b, where a and b are both integers. In the 19th century, Charles Hermite found a proof that requires no p ...
.
Partial fraction expansion
There is a series representation aspartial fraction expansion
In algebra, the partial fraction decomposition or partial fraction expansion of a rational fraction (that is, a fraction such that the numerator and the denominator are both polynomials) is an operation that consists of expressing the fraction as ...
where just translated reciprocal function
In mathematics, a multiplicative inverse or reciprocal for a number ''x'', denoted by 1/''x'' or ''x''−1, is a number which when multiplied by ''x'' yields the multiplicative identity, 1. The multiplicative inverse of a fraction ''a''/''b ...
s are summed up, such that the pole
Pole may refer to:
Astronomy
*Celestial pole, the projection of the planet Earth's axis of rotation onto the celestial sphere; also applies to the axis of rotation of other planets
*Pole star, a visible star that is approximately aligned with the ...
s of the cotangent function and the reciprocal functions match:
:
This identity can be proved with the Herglotz
Gustav Herglotz (2 February 1881 – 22 March 1953) was a Sudeten Germans, German Bohemian physicist best known for his works on the theory of relativity and seismology.
Biography
Gustav Ferdinand Joseph Wenzel Herglotz was born in Volary num. 2 ...
trick.
Combining the th with the th term lead to absolutely convergent
In mathematics, an infinite series of numbers is said to converge absolutely (or to be absolutely convergent) if the sum of the absolute values of the summands is finite. More precisely, a real or complex series \textstyle\sum_^\infty a_n is said ...
series:
:
Similarly, one can find a partial fraction expansion for the secant, cosecant and tangent functions:
:
:
:
:
Infinite product expansion
The following infinite product for the sine is of great importance in complex analysis: : For the proof of this expansion, seeSine
In mathematics, sine and cosine are trigonometric functions of an angle. The sine and cosine of an acute angle are defined in the context of a right triangle: for the specified angle, its sine is the ratio of the length of the side that is oppo ...
. From this, it can be deduced that
:
Relationship to exponential function (Euler's formula)
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
relates sine and cosine to the exponential function
The exponential function is a mathematical function denoted by f(x)=\exp(x) or e^x (where the argument is written as an exponent). Unless otherwise specified, the term generally refers to the positive-valued function of a real variable, a ...
:
:
This formula is commonly considered for real values of , but it remains true for all complex values.
''Proof'': Let and One has for . The quotient rule
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h(x)=f(x)/g(x), where both and are differentiable and g(x)\neq 0. The quotient rule states that the deriva ...
implies thus that . Therefore, is a constant function, which equals , as This proves the formula.
One has
:
Solving this linear system
In systems theory, a linear system is a mathematical model of a system based on the use of a linear operator.
Linear systems typically exhibit features and properties that are much simpler than the nonlinear case.
As a mathematical abstraction o ...
in sine and cosine, one can express them in terms of the exponential function:
:
When is real, this may be rewritten as
:
Most trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
can be proved by expressing trigonometric functions in terms of the complex exponential function by using above formulas, and then using the identity for simplifying the result.
Definitions using functional equations
One can also define the trigonometric functions using variousfunctional equation
In mathematics, a functional equation
is, in the broadest meaning, an equation in which one or several functions appear as unknowns. So, differential equations and integral equations are functional equations. However, a more restricted meaning ...
s.
For example, the sine and the cosine form the unique pair of continuous function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value ...
s that satisfy the difference formula
:
and the added condition
:
In the complex plane
The sine and cosine of acomplex number
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the form ...
can be expressed in terms of real sines, cosines, and hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
s as follows:
:
By taking advantage of domain coloring
In complex analysis, domain coloring or a color wheel graph is a technique for visualizing complex functions by assigning a color to each point of the complex plane. By assigning points on the complex plane to different colors and brightness, d ...
, it is possible to graph the trigonometric functions as complex-valued functions. Various features unique to the complex functions can be seen from the graph; for example, the sine and cosine functions can be seen to be unbounded as the imaginary part of becomes larger (since the color white represents infinity), and the fact that the functions contain simple zeros or poles is apparent from the fact that the hue cycles around each zero or pole exactly once. Comparing these graphs with those of the corresponding Hyperbolic functions highlights the relationships between the two.
Basic identities
Many identities interrelate the trigonometric functions. This section contains the most basic ones; for more identities, seeList of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
. These identities may be proved geometrically from the unit-circle definitions or the right-angled-triangle definitions (although, for the latter definitions, care must be taken for angles that are not in the interval , see Proofs of trigonometric identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of r ...
). For non-geometrical proofs using only tools of calculus
Calculus, originally called infinitesimal calculus or "the calculus of infinitesimals", is the mathematical study of continuous change, in the same way that geometry is the study of shape, and algebra is the study of generalizations of arithm ...
, one may use directly the differential equations, in a way that is similar to that of the above proof of Euler's identity. One can also use Euler's identity for expressing all trigonometric functions in terms of complex exponentials and using properties of the exponential function.
Parity
The cosine and the secant are even functions; the other trigonometric functions areodd function
In mathematics, even functions and odd functions are functions which satisfy particular symmetry relations, with respect to taking additive inverses. They are important in many areas of mathematical analysis, especially the theory of power seri ...
s. That is:
:
Periods
All trigonometric functions areperiodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
s of period . This is the smallest period, except for the tangent and the cotangent, which have as smallest period. This means that, for every integer , one has
:
Pythagorean identity
The Pythagorean identity, is the expression of thePythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
in terms of trigonometric functions. It is
:.
Dividing through by either or gives
:
and
:.
Sum and difference formulas
The sum and difference formulas allow expanding the sine, the cosine, and the tangent of a sum or a difference of two angles in terms of sines and cosines and tangents of the angles themselves. These can be derived geometrically, using arguments that date toPtolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importanc ...
. One can also produce them algebraically using Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
.
; Sum
:
; Difference
:
When the two angles are equal, the sum formulas reduce to simpler equations known as the double-angle formulae
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
.
:
These identities can be used to derive the product-to-sum identities.
By setting all trigonometric functions of can be expressed as rational fraction
In algebra, an algebraic fraction is a fraction whose numerator and denominator are algebraic expressions. Two examples of algebraic fractions are \frac and \frac. Algebraic fractions are subject to the same laws as arithmetic fractions.
A rationa ...
s of :
:
Together with
:
this is the tangent half-angle substitution
In integral calculus, the tangent half-angle substitution is a change of variables used for evaluating integrals, which converts a rational function of trigonometric functions of x into an ordinary rational function of t by setting t = \tan \tfra ...
, which reduces the computation of integral
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented i ...
s and antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically ...
s of trigonometric functions to that of rational fractions.
Derivatives and antiderivatives
Thederivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. F ...
s of trigonometric functions result from those of sine and cosine by applying quotient rule
In calculus, the quotient rule is a method of finding the derivative of a function that is the ratio of two differentiable functions. Let h(x)=f(x)/g(x), where both and are differentiable and g(x)\neq 0. The quotient rule states that the deriva ...
. The values given for the antiderivative
In calculus, an antiderivative, inverse derivative, primitive function, primitive integral or indefinite integral of a function is a differentiable function whose derivative is equal to the original function . This can be stated symbolically ...
s in the following table can be verified by differentiating them. The number is a constant of integration
In calculus, the constant of integration, often denoted by C (or c), is a constant term added to an antiderivative of a function f(x) to indicate that the indefinite integral of f(x) (i.e., the set of all antiderivatives of f(x)), on a connected ...
.
Alternatively, the derivatives of the 'co-functions' can be obtained using trigonometric identities and the chain rule:
:
Inverse functions
The trigonometric functions are periodic, and hence notinjective
In mathematics, an injective function (also known as injection, or one-to-one function) is a function that maps distinct elements of its domain to distinct elements; that is, implies . (Equivalently, implies in the equivalent contrapositiv ...
, so strictly speaking, they do not have an inverse function
In mathematics, the inverse function of a function (also called the inverse of ) is a function that undoes the operation of . The inverse of exists if and only if is bijective, and if it exists, is denoted by f^ .
For a function f\colon X\t ...
. However, on each interval on which a trigonometric function is monotonic
In mathematics, a monotonic function (or monotone function) is a function between ordered sets that preserves or reverses the given order. This concept first arose in calculus, and was later generalized to the more abstract setting of order ...
, one can define an inverse function, and this defines inverse trigonometric functions as multivalued function
In mathematics, a multivalued function, also called multifunction, many-valued function, set-valued function, is similar to a function, but may associate several values to each input. More precisely, a multivalued function from a domain to a ...
s. To define a true inverse function, one must restrict the domain to an interval where the function is monotonic, and is thus bijective
In mathematics, a bijection, also known as a bijective function, one-to-one correspondence, or invertible function, is a function between the elements of two sets, where each element of one set is paired with exactly one element of the other s ...
from this interval to its image by the function. The common choice for this interval, called the set of principal values, is given in the following table. As usual, the inverse trigonometric functions are denoted with the prefix "arc" before the name or its abbreviation of the function.
The notations , , etc. are often used for and , etc. When this notation is used, inverse functions could be confused with multiplicative inverses. The notation with the "arc" prefix avoids such a confusion, though "arcsec" for arcsecant can be confused with "arcsecond
A minute of arc, arcminute (arcmin), arc minute, or minute arc, denoted by the symbol , is a unit of angular measurement equal to of one degree. Since one degree is of a turn (or complete rotation), one minute of arc is of a turn. The na ...
".
Just like the sine and cosine, the inverse trigonometric functions can also be expressed in terms of infinite series. They can also be expressed in terms of complex logarithm
In mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in ...
s.
Applications
Angles and sides of a triangle
In this section , , denote the three (interior) angles of a triangle, and , , denote the lengths of the respective opposite edges. They are related by various formulas, which are named by the trigonometric functions they involve.Law of sines
The law of sines states that for an arbitrary triangle with sides , , and and angles opposite those sides , and : where is the area of the triangle, or, equivalently, where is the triangle'scircumradius
In geometry, the circumscribed circle or circumcircle of a polygon is a circle that passes through all the vertices of the polygon. The center of this circle is called the circumcenter and its radius is called the circumradius.
Not every polyg ...
.
It can be proved by dividing the triangle into two right ones and using the above definition of sine. The law of sines is useful for computing the lengths of the unknown sides in a triangle if two angles and one side are known. This is a common situation occurring in ''triangulation
In trigonometry and geometry, triangulation is the process of determining the location of a point by forming triangles to the point from known points.
Applications
In surveying
Specifically in surveying, triangulation involves only angle me ...
'', a technique to determine unknown distances by measuring two angles and an accessible enclosed distance.
Law of cosines
The law of cosines (also known as the cosine formula or cosine rule) is an extension of thePythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
:
or equivalently,
In this formula the angle at is opposite to the side . This theorem can be proved by dividing the triangle into two right ones and using the Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a fundamental relation in Euclidean geometry between the three sides of a right triangle. It states that the area of the square whose side is the hypotenuse (the side opposite t ...
.
The law of cosines can be used to determine a side of a triangle if two sides and the angle between them are known. It can also be used to find the cosines of an angle (and consequently the angles themselves) if the lengths of all the sides are known.
Law of tangents
The law of tangents says that: :.Law of cotangents
If ''s'' is the triangle's semiperimeter, (''a'' + ''b'' + ''c'')/2, and ''r'' is the radius of the triangle'sincircle
In geometry, the incircle or inscribed circle of a triangle is the largest circle that can be contained in the triangle; it touches (is tangent to) the three sides. The center of the incircle is a triangle center called the triangle's incenter.
...
, then ''rs'' is the triangle's area. Therefore Heron's formula
In geometry, Heron's formula (or Hero's formula) gives the area of a triangle in terms of the three side lengths , , . If s = \tfrac12(a + b + c) is the semiperimeter of the triangle, the area is,
:A = \sqrt.
It is named after first-century ...
implies that:
:.
The law of cotangents says that:
:
It follows that
:
Periodic functions

 The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe
The trigonometric functions are also important in physics. The sine and the cosine functions, for example, are used to describe simple harmonic motion
In mechanics and physics, simple harmonic motion (sometimes abbreviated ) is a special type of periodic motion of a body resulting from a dynamic equilibrium between an inertial force, proportional to the acceleration of the body away from the ...
, which models many natural phenomena, such as the movement of a mass attached to a spring and, for small angles, the pendular motion of a mass hanging by a string. The sine and cosine functions are one-dimensional projections of uniform circular motion
In physics, circular motion is a movement of an object along the circumference of a circle or rotation along a circular path. It can be uniform, with constant angular rate of rotation and constant speed, or non-uniform with a changing rate of rot ...
.
Trigonometric functions also prove to be useful in the study of general periodic function
A periodic function is a function that repeats its values at regular intervals. For example, the trigonometric functions, which repeat at intervals of 2\pi radians, are periodic functions. Periodic functions are used throughout science to desc ...
s. The characteristic wave patterns of periodic functions are useful for modeling recurring phenomena such as sound or light wave
In physics, mathematics, and related fields, a wave is a propagating dynamic disturbance (change from equilibrium) of one or more quantities. Waves can be periodic, in which case those quantities oscillate repeatedly about an equilibrium (res ...
s.
Under rather general conditions, a periodic function can be expressed as a sum of sine waves or cosine waves in a Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''p ...
. Denoting the sine or cosine basis functions
In mathematics, a basis function is an element of a particular basis for a function space. Every function in the function space can be represented as a linear combination of basis functions, just as every vector in a vector space can be repres ...
by , the expansion of the periodic function takes the form:
For example, the square wave
A square wave is a non-sinusoidal periodic waveform in which the amplitude alternates at a steady frequency between fixed minimum and maximum values, with the same duration at minimum and maximum. In an ideal square wave, the transitions b ...
can be written as the Fourier series
A Fourier series () is a summation of harmonically related sinusoidal functions, also known as components or harmonics. The result of the summation is a periodic function whose functional form is determined by the choices of cycle length (or ''p ...
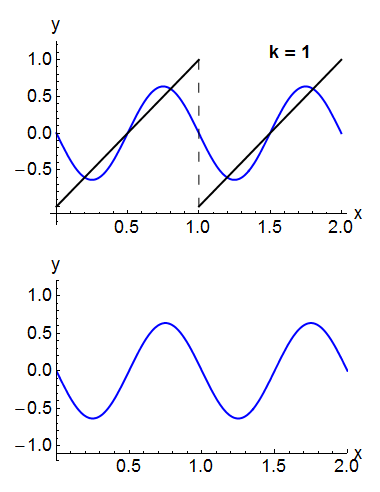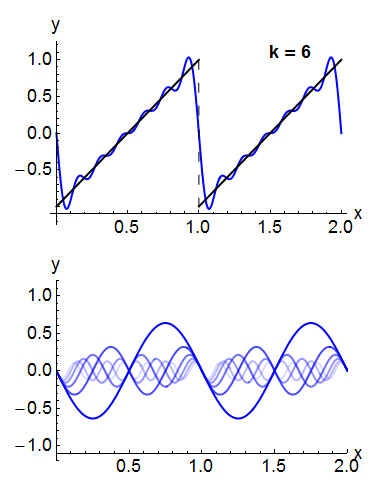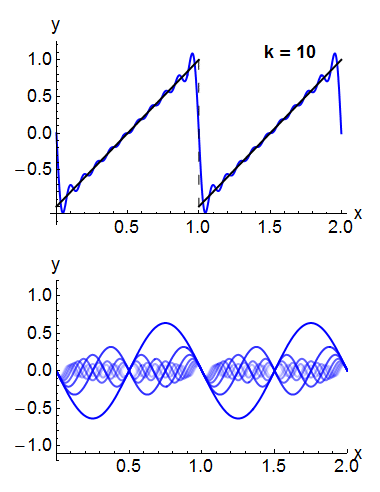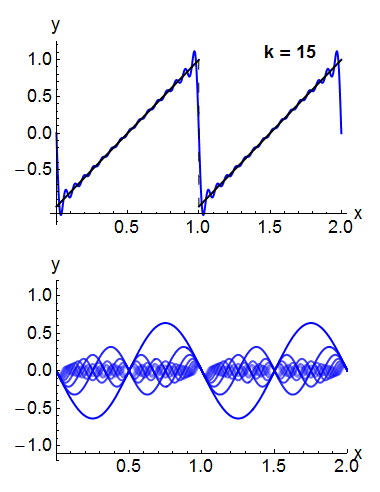
In the animation of a square wave at top right it can be seen that just a few terms already produce a fairly good approximation. The superposition of several terms in the expansion of a sawtooth wave
The sawtooth wave (or saw wave) is a kind of non-sinusoidal waveform. It is so named based on its resemblance to the teeth of a plain-toothed saw with a zero rake angle. A single sawtooth, or an intermittently triggered sawtooth, is called a ...
are shown underneath.
History
While the early study of trigonometry can be traced to antiquity, the trigonometric functions as they are in use today were developed in the medieval period. The chord function was discovered byHipparchus
Hipparchus (; el, Ἵππαρχος, ''Hipparkhos''; BC) was a Greek astronomer, geographer, and mathematician. He is considered the founder of trigonometry, but is most famous for his incidental discovery of the precession of the equi ...
of Nicaea
Nicaea, also known as Nicea or Nikaia (; ; grc-gre, Νίκαια, ) was an ancient Greek city in Bithynia, where located in northwestern Anatolia and is primarily known as the site of the First and Second Councils of Nicaea (the first and seve ...
(180–125 BCE) and Ptolemy
Claudius Ptolemy (; grc-gre, Πτολεμαῖος, ; la, Claudius Ptolemaeus; AD) was a mathematician, astronomer, astrologer, geographer, and music theorist, who wrote about a dozen scientific treatises, three of which were of importanc ...
of Roman Egypt
, conventional_long_name = Roman Egypt
, common_name = Egypt
, subdivision = Province
, nation = the Roman Empire
, era = Late antiquity
, capital = Alexandria
, title_leader = Praefectus Augustalis
, image_map = Roman E ...
(90–165 CE). The functions of sine and versine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit Āryabhaṭa's sine table , ''Aryabhatia'',
(1 – cosine) can be traced back to the ''jyā'' and ''koti-jyā'' functions used in Gupta period
The Gupta Empire was an ancient Indian empire which existed from the early 4th century CE to late 6th century CE. At its zenith, from approximately 319 to 467 CE, it covered much of the Indian subcontinent. This period is considered as the Gold ...
Indian astronomy
Astronomy has long history in Indian subcontinent stretching from pre-historic to modern times. Some of the earliest roots of Indian astronomy can be dated to the period of Indus Valley civilisation or earlier. Astronomy later developed as a dis ...
(''Aryabhatiya
''Aryabhatiya'' (IAST: ') or ''Aryabhatiyam'' ('), a Sanskrit astronomical treatise, is the ''magnum opus'' and only known surviving work of the 5th century Indian mathematician Aryabhata. Philosopher of astronomy Roger Billard estimates that th ...
'', ''Surya Siddhanta
The ''Surya Siddhanta'' (; ) is a Sanskrit treatise in Indian astronomy dated to 505 CE,Menso Folkerts, Craig G. Fraser, Jeremy John Gray, John L. Berggren, Wilbur R. Knorr (2017)Mathematics Encyclopaedia Britannica, Quote: "(...) its Hindu inven ...
''), via translation from Sanskrit to Arabic and then from Arabic to Latin. (See Aryabhata's sine table.)
All six trigonometric functions in current use were known in Islamic mathematics
Mathematics during the Golden Age of Islam, especially during the 9th and 10th centuries, was built on Greek mathematics (Euclid, Archimedes, Apollonius) and Indian mathematics (Aryabhata, Brahmagupta). Important progress was made, such as full ...
by the 9th century, as was the law of sines
In trigonometry, the law of sines, sine law, sine formula, or sine rule is an equation relating the lengths of the sides of any triangle to the sines of its angles. According to the law,
\frac \,=\, \frac \,=\, \frac \,=\, 2R,
where , and a ...
, used in solving triangles. With the exception of the sine (which was adopted from Indian mathematics), the other five modern trigonometric functions were discovered by Persian and Arab mathematicians, including the cosine, tangent, cotangent, secant and cosecant. Al-Khwārizmī
Muḥammad ibn Mūsā al-Khwārizmī ( ar, محمد بن موسى الخوارزمي, Muḥammad ibn Musā al-Khwārazmi; ), or al-Khwarizmi, was a Persian polymath from Khwarazm, who produced vastly influential works in mathematics, astronom ...
(c. 780–850) produced tables of sines, cosines and tangents. Circa 830, Habash al-Hasib al-Marwazi
Ahmad ibn 'Abdallah Habash Hasib Marwazi (766 - d. after 869 in Samarra, Iraq ) was a north-eastern Iranian astronomer, geographer, and mathematician from Merv in Khorasan who for the first time described the trigonometric ratios: sine, cosine, ...
discovered the cotangent, and produced tables of tangents and cotangents.Jacques Sesiano, "Islamic mathematics", p. 157, in Muhammad ibn Jābir al-Harrānī al-Battānī
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astron ...
(853–929) discovered the reciprocal functions of secant and cosecant, and produced the first table of cosecants for each degree from 1° to 90°. The trigonometric functions were later studied by mathematicians including Omar Khayyám
Ghiyāth al-Dīn Abū al-Fatḥ ʿUmar ibn Ibrāhīm Nīsābūrī (18 May 1048 – 4 December 1131), commonly known as Omar Khayyam ( fa, عمر خیّام), was a polymath, known for his contributions to mathematics, astronomy, philosophy, an ...
, Bhāskara II
Bhāskara II (c. 1114–1185), also known as Bhāskarāchārya ("Bhāskara, the teacher"), and as Bhāskara II to avoid confusion with Bhāskara I, was an Indian mathematician and astronomer. From verses, in his main work, Siddhānta Shiroman ...
, Nasir al-Din al-Tusi
Muhammad ibn Muhammad ibn al-Hasan al-Tūsī ( fa, محمد ابن محمد ابن حسن طوسی 18 February 1201 – 26 June 1274), better known as Nasir al-Din al-Tusi ( fa, نصیر الدین طوسی, links=no; or simply Tusi in the West ...
, Jamshīd al-Kāshī
Ghiyāth al-Dīn Jamshīd Masʿūd al-Kāshī (or al-Kāshānī) ( fa, غیاث الدین جمشید کاشانی ''Ghiyās-ud-dīn Jamshīd Kāshānī'') (c. 1380 Kashan, Iran – 22 June 1429 Samarkand, Transoxania) was a Persian astronomer a ...
(14th century), Ulugh Beg
Mīrzā Muhammad Tāraghay bin Shāhrukh ( chg, میرزا محمد طارق بن شاہ رخ, fa, میرزا محمد تراغای بن شاہ رخ), better known as Ulugh Beg () (22 March 1394 – 27 October 1449), was a Timurid sultan, as ...
(14th century), Regiomontanus
Johannes Müller von Königsberg (6 June 1436 – 6 July 1476), better known as Regiomontanus (), was a mathematician, astrologer and astronomer of the German Renaissance, active in Vienna, Buda and Nuremberg. His contributions were instrumental ...
(1464), Rheticus, and Rheticus' student Valentinus Otho
Valentinus Otho (also Valentin Otto; born around 1545–46 possibly in Magdeburg – 8 April 1603 in Heidelberg) was a German mathematician and astronomer.
Life
In 1573 he came to Wittenberg, proposing to Johannes Praetorius an approximation of ...
.
Madhava of Sangamagrama
Iriññāttappiḷḷi Mādhavan known as Mādhava of Sangamagrāma () was an Indian mathematician and astronomer from the town believed to be present-day Kallettumkara, Aloor Panchayath, Irinjalakuda in Thrissur District, Kerala, India. He is ...
(c. 1400) made early strides in the analysis
Analysis ( : analyses) is the process of breaking a complex topic or substance into smaller parts in order to gain a better understanding of it. The technique has been applied in the study of mathematics and logic since before Aristotle (38 ...
of trigonometric functions in terms of infinite series
In mathematics, a series is, roughly speaking, a description of the operation of adding infinitely many quantities, one after the other, to a given starting quantity. The study of series is a major part of calculus and its generalization, math ...
. (See Madhava series
In mathematics, a Madhava series or Leibniz series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by an Indian Mathematician and Astronomer Madhava of Sangamagrama (c.&nb ...
and Madhava's sine table
Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.5 ...
.)
The tangent function was brought to Europe by Giovanni Bianchini
Giovanni Bianchini (in Latin, Johannes Blanchinus) (1410 – c. 1469) was a professor of mathematics and astronomy at the University of Ferrara and court astrologer of Leonello d'Este. He was an associate of Georg Purbach and Regiomontanus. ...
in 1467 in trigonometry tables he created to support the calculation of stellar coordinates.
The terms ''tangent'' and ''secant'' were first introduced by the Danish mathematician Thomas Fincke
Thomas Fincke (6 January 1561 – 24 April 1656) was a Danish mathematician and physicist, and a professor at the University of Copenhagen for more than 60 years.
Biography
Thomas Jacobsen Fincke was born in Flensburg in Schleswig.
Fincke was ...
in his book ''Geometria rotundi'' (1583).
The 17th century French mathematician Albert Girard
Albert Girard () (11 October 1595 in Saint-Mihiel, France − 8 December 1632 in Leiden, The Netherlands) was a French-born mathematician. He studied at the University of Leiden. He "had early thoughts on the fundamental theorem of algebra" and g ...
made the first published use of the abbreviations ''sin'', ''cos'', and ''tan'' in his book ''Trigonométrie''.
In a paper published in 1682, Gottfried Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mathem ...
proved that is not an algebraic function In mathematics, an algebraic function is a function that can be defined
as the root of a polynomial equation. Quite often algebraic functions are algebraic expressions using a finite number of terms, involving only the algebraic operations additi ...
of . Though introduced as ratios of sides of a right triangle
A right triangle (American English) or right-angled triangle (British), or more formally an orthogonal triangle, formerly called a rectangled triangle ( grc, ὀρθόσγωνία, lit=upright angle), is a triangle in which one angle is a right an ...
, and thus appearing to be rational function
In mathematics, a rational function is any function that can be defined by a rational fraction, which is an algebraic fraction such that both the numerator and the denominator are polynomials. The coefficients of the polynomials need not be rat ...
s, Leibnitz result established that they are actually transcendental function
In mathematics, a transcendental function is an analytic function that does not satisfy a polynomial equation, in contrast to an algebraic function.
In other words, a transcendental function "transcends" algebra in that it cannot be expressed alge ...
s of their argument. The task of assimilating circular functions into algebraic expressions was accomplished by Euler in his ''Introduction to the Analysis of the Infinite
''Introductio in analysin infinitorum'' (Latin: ''Introduction to the Analysis of the Infinite'') is a two-volume work by Leonhard Euler which lays the foundations of mathematical analysis. Written in Latin and published in 1748, the ''Introducti ...
'' (1748). His method was to show that the sine and cosine functions are alternating series
In mathematics, an alternating series is an infinite series of the form
\sum_^\infty (-1)^n a_n or \sum_^\infty (-1)^ a_n
with for all . The signs of the general terms alternate between positive and negative. Like any series, an alternatin ...
formed from the even and odd terms respectively of the exponential series. He presented "Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the fundamental relationship between the trigonometric functions and the complex exponential function. Euler's formula states that for an ...
", as well as near-modern abbreviations (''sin.'', ''cos.'', ''tang.'', ''cot.'', ''sec.'', and ''cosec.'').
A few functions were common historically, but are now seldom used, such as the chord, the versine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit Āryabhaṭa's sine table , ''Aryabhatia'',
(which appeared in the earliest tables), the coversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',haversine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit ''Aryabhatia'',exsecant
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, civil engineering, astro ...
and the excosecant
The exsecant (exsec, exs) and excosecant (excosec, excsc, exc) are trigonometric functions defined in terms of the secant (trigonometry), secant and cosecant functions. They used to be important in fields such as surveying, railway engineering, ci ...
. The list of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
shows more relations between these functions.
*
*
*
*
*
*
Etymology
The word derives fromLatin
Latin (, or , ) is a classical language belonging to the Italic branch of the Indo-European languages. Latin was originally a dialect spoken in the lower Tiber area (then known as Latium) around present-day Rome, but through the power of the ...
''sinus
Sinus may refer to:
Anatomy
* Sinus (anatomy), a sac or cavity in any organ or tissue
** Paranasal sinuses, air cavities in the cranial bones, especially those near the nose, including:
*** Maxillary sinus, is the largest of the paranasal sinuses, ...
'', meaning "bend; bay", and more specifically "the hanging fold of the upper part of a toga
The toga (, ), a distinctive garment of ancient Rome, was a roughly semicircular cloth, between in length, draped over the shoulders and around the body. It was usually woven from white wool, and was worn over a tunic. In Roman historical tra ...
", "the bosom of a garment", which was chosen as the translation of what was interpreted as the Arabic word ''jaib'', meaning "pocket" or "fold" in the twelfth-century translations of works by Al-Battani
Abū ʿAbd Allāh Muḥammad ibn Jābir ibn Sinān al-Raqqī al-Ḥarrānī aṣ-Ṣābiʾ al-Battānī ( ar, محمد بن جابر بن سنان البتاني) ( Latinized as Albategnius, Albategni or Albatenius) (c. 858 – 929) was an astron ...
and al-Khwārizmī
Muḥammad ibn Mūsā al-Khwārizmī ( ar, محمد بن موسى الخوارزمي, Muḥammad ibn Musā al-Khwārazmi; ), or al-Khwarizmi, was a Persian polymath from Khwarazm, who produced vastly influential works in mathematics, astronom ...
into Medieval Latin
Medieval Latin was the form of Literary Latin used in Roman Catholic Western Europe during the Middle Ages. In this region it served as the primary written language, though local languages were also written to varying degrees. Latin functioned ...
.
The choice was based on a misreading of the Arabic written form ''j-y-b'' (), which itself originated as a transliteration
Transliteration is a type of conversion of a text from one writing system, script to another that involves swapping Letter (alphabet), letters (thus ''wikt:trans-#Prefix, trans-'' + ''wikt:littera#Latin, liter-'') in predictable ways, such as ...
from Sanskrit ', which along with its synonym ' (the standard Sanskrit term for the sine) translates to "bowstring", being in turn adopted from Ancient Greek
Ancient Greek includes the forms of the Greek language used in ancient Greece and the ancient world from around 1500 BC to 300 BC. It is often roughly divided into the following periods: Mycenaean Greek (), Dark Ages (), the Archaic peri ...
"string".
The word ''tangent'' comes from Latin ''tangens'' meaning "touching", since the line ''touches'' the circle of unit radius, whereas ''secant'' stems from Latin ''secans''—"cutting"—since the line ''cuts'' the circle.Oxford English Dictionary
The prefix " co-" (in "cosine", "cotangent", "cosecant") is found in Edmund Gunter
Edmund Gunter (158110 December 1626), was an English clergyman, mathematician, geometer and astronomer of Welsh descent. He is best remembered for his mathematical contributions which include the invention of the Gunter's chain, the Gunter's qu ...
's ''Canon triangulorum'' (1620), which defines the ''cosinus'' as an abbreviation for the ''sinus complementi'' (sine of the complementary angle
In Euclidean geometry, an angle is the figure formed by two rays, called the '' sides'' of the angle, sharing a common endpoint, called the ''vertex'' of the angle.
Angles formed by two rays lie in the plane that contains the rays. Angles ar ...
) and proceeds to define the ''cotangens'' similarly.
See also
*All Students Take Calculus
All or ALL may refer to:
Language
* All, an indefinite pronoun in English
* All, one of the English determiners
* Allar language (ISO 639-3 code)
* Allative case (abbreviated ALL)
Music
* All (band), an American punk rock band
* ''All'' (All al ...
– a mnemonic for recalling the signs of trigonometric functions in a particular quadrant of a Cartesian plane
* Bhaskara I's sine approximation formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian ma ...
* Differentiation of trigonometric functions
The differentiation of trigonometric functions is the mathematical process of finding the derivative of a trigonometric function, or its rate of change with respect to a variable. For example, the derivative of the sine function is written sin′ ...
* Generalized trigonometry
Ordinary trigonometry studies triangles in the Euclidean space, Euclidean plane . There are a number of ways of defining the ordinary Euclidean geometry, Euclidean geometric trigonometric functions on real numbers, for example trigonometric funct ...
* Generating trigonometric tables
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables ...
* Hyperbolic function
In mathematics, hyperbolic functions are analogues of the ordinary trigonometric functions, but defined using the hyperbola rather than the circle. Just as the points form a circle with a unit radius, the points form the right half of the u ...
* List of integrals of trigonometric functions
The following is a list of integrals (antiderivative functions) of trigonometric functions. For antiderivatives involving both exponential and trigonometric functions, see List of integrals of exponential functions. For a complete list of antid ...
* List of periodic functions
This is a list of some well-known periodic functions. The constant function , where is independent of , is periodic with any period, but lacks a ''fundamental period''. A definition is given for some of the following functions, though each funct ...
* List of trigonometric identities
In trigonometry, trigonometric identities are equalities that involve trigonometric functions and are true for every value of the occurring variables for which both sides of the equality are defined. Geometrically, these are identities involvin ...
* Polar sine In geometry, the polar sine generalizes the sine function of angle to the vertex angle of a polytope. It is denoted by psin.
Definition
''n'' vectors in ''n''-dimensional space
Let v1, ..., v''n'' (''n'' ≥ 2) be non-zer ...
– a generalization to vertex angles
* Proofs of trigonometric identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of r ...
* Versine
The versine or versed sine is a trigonometric function found in some of the earliest (Sanskrit Āryabhaṭa's sine table , ''Aryabhatia'',
– for several less used trigonometric functions
Notes
References
* *Lars Ahlfors
Lars Valerian Ahlfors (18 April 1907 – 11 October 1996) was a Finnish mathematician, remembered for his work in the field of Riemann surfaces and his text on complex analysis.
Background
Ahlfors was born in Helsinki, Finland. His mother, S ...
, ''Complex Analysis: an introduction to the theory of analytic functions of one complex variable'', second edition, McGraw-Hill Book Company
McGraw Hill is an American educational publishing company and one of the "big three" educational publishers that publishes educational content, software, and services for pre-K through postgraduate education. The company also publishes referen ...
, New York, 1966.
* Boyer, Carl B., ''A History of Mathematics'', John Wiley & Sons, Inc., 2nd edition. (1991). .
*
* Gal, Shmuel and Bachelis, Boris. An accurate elementary mathematical library for the IEEE floating point standard, ACM Transactions on Mathematical Software (1991).
* Joseph, George G., ''The Crest of the Peacock: Non-European Roots of Mathematics'', 2nd ed. Penguin Books
Penguin Books is a British publishing, publishing house. It was co-founded in 1935 by Allen Lane with his brothers Richard and John, as a line of the publishers The Bodley Head, only becoming a separate company the following year.Trigonometric Delights
', Princeton Univ. Press. (1998). Reprint edition (2002): . * Needham, Tristan
"Preface"
to
Visual Complex Analysis
'. Oxford University Press, (1999). . * * O'Connor, J. J., and E. F. Robertson
''
"Madhava of Sangamagramma"
''
"Madhava of Sangamagramma"
, ''
"Tangent"
from ''
Visionlearning Module on Wave Mathematics
GonioLab
Visualization of the unit circle, trigonometric and hyperbolic functions
Article about the
q-Cosine
Article about the
', Princeton Univ. Press. (1998). Reprint edition (2002): . * Needham, Tristan
"Preface"
to
Visual Complex Analysis
'. Oxford University Press, (1999). . * * O'Connor, J. J., and E. F. Robertson
''
MacTutor History of Mathematics archive
The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland. It contains detailed biographies on many historical and contemporary mathemati ...
''. (1996).
* O'Connor, J. J., and E. F. Robertson"Madhava of Sangamagramma"
''
MacTutor History of Mathematics archive
The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland. It contains detailed biographies on many historical and contemporary mathemati ...
''. (2000).
* Pearce, Ian G."Madhava of Sangamagramma"
, ''
MacTutor History of Mathematics archive
The MacTutor History of Mathematics archive is a website maintained by John J. O'Connor and Edmund F. Robertson and hosted by the University of St Andrews in Scotland. It contains detailed biographies on many historical and contemporary mathemati ...
''. (2002).
*
* Weisstein, Eric W."Tangent"
from ''
MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Dig ...
'', accessed 21 January 2006.
External links
*Visionlearning Module on Wave Mathematics
GonioLab
Visualization of the unit circle, trigonometric and hyperbolic functions
Article about the
q-analog
In mathematics, a ''q''-analog of a theorem, identity or expression is a generalization involving a new parameter ''q'' that returns the original theorem, identity or expression in the limit as . Typically, mathematicians are interested in ''q''- ...
of sin at MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Dig ...
q-Cosine
Article about the
q-analog
In mathematics, a ''q''-analog of a theorem, identity or expression is a generalization involving a new parameter ''q'' that returns the original theorem, identity or expression in the limit as . Typically, mathematicians are interested in ''q''- ...
of cos at MathWorld
''MathWorld'' is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Dig ...
{{DEFAULTSORT:Trigonometric Functions
Angle
Trigonometry
Elementary special functions
Analytic functions
Ratios
Dimensionless numbers