|
Proofs Of Trigonometric Identities
There are several equivalent ways for defining trigonometric functions, and the proof of the trigonometric identities between them depend on the chosen definition. The oldest and somehow the most elementary definition is based on the geometry of right triangles. The proofs given in this article use this definition, and thus apply to non-negative angles not greater than a right angle. For greater and negative angles, see Trigonometric functions. Other definitions, and therefore other proofs are based on the Taylor series of sine and cosine, or on the differential equation f''+f=0 to which they are solutions. Elementary trigonometric identities Definitions The six trigonometric functions are defined for every real number, except, for some of them, for angles that differ from 0 by a multiple of the right angle (90°). Referring to the diagram at the right, the six trigonometric functions of θ are, for angles smaller than the right angle: : \sin \theta = \frac = \frac : \c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Trigonometric Function
In mathematics, the trigonometric functions (also called circular functions, angle functions or goniometric functions) are real functions which relate an angle of a right-angled triangle to ratios of two side lengths. They are widely used in all sciences that are related to geometry, such as navigation, solid mechanics, celestial mechanics, geodesy, and many others. They are among the simplest periodic functions, and as such are also widely used for studying periodic phenomena through Fourier analysis. The trigonometric functions most widely used in modern mathematics are the sine, the cosine, and the tangent. Their reciprocals are respectively the cosecant, the secant, and the cotangent, which are less used. Each of these six trigonometric functions has a corresponding inverse function, and an analog among the hyperbolic functions. The oldest definitions of trigonometric functions, related to right-angle triangles, define them only for acute angles. To extend the sine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Arc Length
ARC may refer to: Business * Aircraft Radio Corporation, a major avionics manufacturer from the 1920s to the '50s * Airlines Reporting Corporation, an airline-owned company that provides ticket distribution, reporting, and settlement services * Airport Regions Conference, a European organization of major airports * Amalgamated Roadstone Corporation, a British stone quarrying company * American Record Company (1904–1908, re-activated 1979), one of two United States record labels by this name * American Record Corporation (1929–1938), a United States record label also known as American Record Company * ARC (American Recording Company) (1978-present), a vanity label for Earth, Wind & Fire * ARC Document Solutions, a company based in California, formerly American Reprographics Company * Amey Roadstone Construction, a former British construction company * Aqaba Railway Corporation, a freight railway in Jordan * ARC/Architectural Resources Cambridge, Inc., Cambridge, Massachuse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cambridge University Press
Cambridge University Press is the university press of the University of Cambridge. Granted letters patent by King Henry VIII in 1534, it is the oldest university press in the world. It is also the King's Printer. Cambridge University Press is a department of the University of Cambridge and is both an academic and educational publisher. It became part of Cambridge University Press & Assessment, following a merger with Cambridge Assessment in 2021. With a global sales presence, publishing hubs, and offices in more than 40 countries, it publishes over 50,000 titles by authors from over 100 countries. Its publishing includes more than 380 academic journals, monographs, reference works, school and university textbooks, and English language teaching and learning publications. It also publishes Bibles, runs a bookshop in Cambridge, sells through Amazon, and has a conference venues business in Cambridge at the Pitt Building and the Sir Geoffrey Cass Sports and Social Centre. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
A Course Of Modern Analysis
''A Course of Modern Analysis: an introduction to the general theory of infinite processes and of analytic functions; with an account of the principal transcendental functions'' (colloquially known as Whittaker and Watson) is a landmark textbook on mathematical analysis written by Edmund T. Whittaker and George N. Watson, first published by Cambridge University Press in 1902. The first edition was Whittaker's alone, but later editions were co-authored with Watson. History Its first, second, third, and the fourth edition were published in 1902, 1915, 1920, and 1927, respectively. Since then, it has continuously been reprinted and is still in print today. A revised, expanded and digitally reset fifth edition, edited by Victor H. Moll, was published in 2021. The book is notable for being the standard reference and textbook for a generation of Cambridge mathematicians including Littlewood and Godfrey H. Hardy. Mary L. Cartwright studied it as preparation for her final hono ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Unit Vector
In mathematics, a unit vector in a normed vector space is a vector (often a spatial vector) of length 1. A unit vector is often denoted by a lowercase letter with a circumflex, or "hat", as in \hat (pronounced "v-hat"). The term ''direction vector'', commonly denoted as d, is used to describe a unit vector being used to represent spatial direction and relative direction. 2D spatial directions are numerically equivalent to points on the unit circle and spatial directions in 3D are equivalent to a point on the unit sphere. The normalized vector û of a non-zero vector u is the unit vector in the direction of u, i.e., :\mathbf = \frac where , u, is the norm (or length) of u. The term ''normalized vector'' is sometimes used as a synonym for ''unit vector''. Unit vectors are often chosen to form the basis of a vector space, and every vector in the space may be written as a linear combination of unit vectors. Orthogonal coordinates Cartesian coordinates Unit vectors ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Madhava Series
In mathematics, a Madhava series or Leibniz series is any one of the series in a collection of infinite series expressions all of which are believed to have been discovered by an Indian Mathematician and Astronomer Madhava of Sangamagrama (c. 1350 – c. 1425), the founder of the Kerala school of astronomy and mathematics and later by Gottfried Wilhelm Leibniz, among others. These expressions are the Maclaurin series expansions of the trigonometric sine, cosine and arctangent functions, and the special case of the power series expansion of the arctangent function yielding a formula for computing . The power series expansions of sine and cosine functions are respectively called ''Madhava's sine series'' and ''Madhava's cosine series''. The power series expansion of the arctangent function is sometimes called ''Madhava–Gregory series'' or ''Gregory–Madhava series''. These power series are also collectively called ''Taylor–Madhava series''. The formula for is r ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Table Of Newtonian Series
In mathematics, a Newtonian series, named after Isaac Newton, is a sum over a sequence a_n written in the form :f(s) = \sum_^\infty (-1)^n a_n = \sum_^\infty \frac a_n where : is the binomial coefficient and (s)_n is the falling factorial. Newtonian series often appear in relations of the form seen in umbral calculus. List The generalized binomial theorem gives : (1+z)^s = \sum_^z^n = 1+z+z^2+\cdots. A proof for this identity can be obtained by showing that it satisfies the differential equation : (1+z) \frac = s (1+z)^s. The digamma function: :\psi(s+1)=-\gamma-\sum_^\infty \frac . The Stirling numbers of the second kind are given by the finite sum :\left\ =\frac\sum_^(-1)^ j^n. This formula is a special case of the ''k''th forward difference of the monomial ''x''''n'' evaluated at ''x'' = 0: : \Delta^k x^n = \sum_^(-1)^ (x+j)^n. A related identity forms the basis of the Nörlund–Rice integral: :\sum_^n \frac = \frac = \frac= B(n+1,s-n),s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
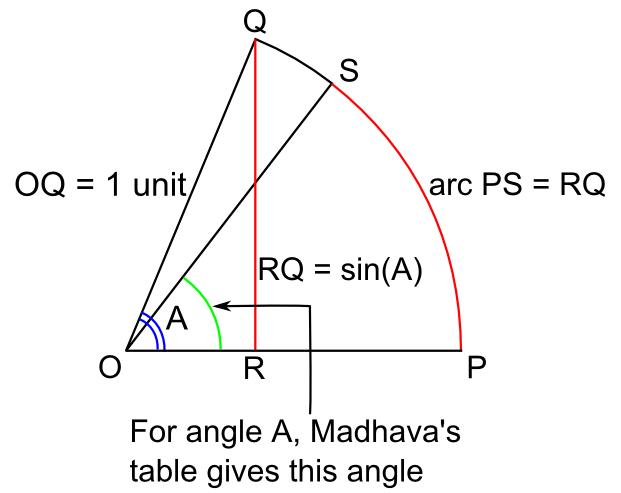
Madhava's Sine Table
Madhava's sine table is the table of trigonometric sines of various angles constructed by the 14th century Kerala mathematician-astronomer Madhava of Sangamagrama. The table lists the trigonometric sines of the twenty-four angles 3.75°, 7.50°, 11.25°, ..., and 90.00° (angles that are integral multiples of 3.75°, i.e. 1/24 of a right angle, beginning with 3.75 and ending with 90.00). The table is encoded in the letters of Devanagari using the Katapayadi system. This gives the entries in the table an appearance of the verses of a poem in Sanskrit. Madhava's original work containing the sine table has not yet been traced. The table is seen reproduced in the ''Aryabhatiyabhashya'' of Nilakantha Somayaji''The Aryabhatiam of Aryabhattacharya with the Bhashya of Nilakantha Somasutvan, Part1-Gaṇitapāda,'' Edited by K. Sambasiva Sastri, Trivandrum Sanskrit Series No.101. p. 55. https://archive.org/details/Trivandrum_Sanskrit_Series_TSS http://www.sanskritebooks.org/2013/0 ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generating Trigonometric Tables
In mathematics, tables of trigonometric functions are useful in a number of areas. Before the existence of pocket calculators, trigonometric tables were essential for navigation, science and engineering. The calculation of mathematical tables was an important area of study, which led to the development of the first mechanical computing devices. Modern computers and pocket calculators now generate trigonometric function values on demand, using special libraries of mathematical code. Often, these libraries use pre-calculated tables internally, and compute the required value by using an appropriate interpolation method. Interpolation of simple look-up tables of trigonometric functions is still used in computer graphics, where only modest accuracy may be required and speed is often paramount. Another important application of trigonometric tables and generation schemes is for fast Fourier transform (FFT) algorithms, where the same trigonometric function values (called ''twiddle ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
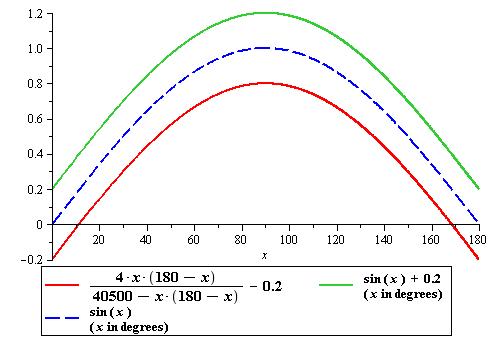
Bhaskara I's Sine Approximation Formula
In mathematics, Bhaskara I's sine approximation formula is a rational expression in one variable for the computation of the approximate values of the trigonometric sines discovered by Bhaskara I (c. 600 – c. 680), a seventh-century Indian mathematician. This formula is given in his treatise titled ''Mahabhaskariya''. It is not known how Bhaskara I arrived at his approximation formula. However, several historians of mathematics have put forward different hypotheses as to the method Bhaskara might have used to arrive at his formula. The formula is elegant, simple and enables one to compute reasonably accurate values of trigonometric sines without using any geometry whatsoever. The approximation formula The formula is given in verses 17 – 19, Chapter VII, Mahabhaskariya of Bhaskara I. A translation of the verses is given below: *(Now) I briefly state the rule (for finding the ''bhujaphala'' and the ''kotiphala'', etc.) without making use of the Rsine-differences 225, etc. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Derivative
In mathematics, the derivative of a function of a real variable measures the sensitivity to change of the function value (output value) with respect to a change in its argument (input value). Derivatives are a fundamental tool of calculus. For example, the derivative of the position of a moving object with respect to time is the object's velocity: this measures how quickly the position of the object changes when time advances. The derivative of a function of a single variable at a chosen input value, when it exists, is the slope of the tangent line to the graph of the function at that point. The tangent line is the best linear approximation of the function near that input value. For this reason, the derivative is often described as the "instantaneous rate of change", the ratio of the instantaneous change in the dependent variable to that of the independent variable. Derivatives can be generalized to functions of several real variables. In this generalization, the de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |