Cl (elliptic Function)

In mathematics, the lemniscate elliptic functions are elliptic functions related to the arc length of the lemniscate of Bernoulli. They were first studied by Giulio Fagnano in 1718 and later by Leonhard Euler and Carl Friedrich Gauss, among others.

The lemniscate sine and lemniscate cosine functions, usually written with the symbols and (sometimes the symbols and or and are used instead) are analogous to the trigonometric functions sine and cosine. While the trigonometric sine relates the arc length to the chord length in a unit-diameter circle $x^2+y^2 = x,$ the lemniscate sine relates the arc length to the chord length of a lemniscate $\bigl(x^2+y^2\bigr)^2=x^2-y^2.$

The lemniscate functions have periods related to a number called the lemniscate constant, the ratio of a lemniscate's perimeter to its diameter. This number is a quartic analog of the ( quadratic) , ratio of perimeter to diameter of a circle.

As complex functions, and have a square period lattice (a multiple of the Gaussian integers) with fundamental periods $\,$ and are a special case of two Jacobi elliptic functions on that lattice, $\operatorname z = \operatorname(z; i),$ $\operatorname z = \operatorname(z; i)$.

Similarly, the hyperbolic lemniscate sine and hyperbolic lemniscate cosine have a square period lattice with fundamental periods $\bigl\.$

The lemniscate functions and the hyperbolic lemniscate functions are related to the Weierstrass elliptic function $\wp (z;a,0)$.

Lemniscate sine and cosine functions

Definitions

The lemniscate functions and can be defined as the solution to the initial value problem:

:$\frac \operatorname z = \bigl(1 + \operatorname^2 z\bigr)\operatornamez,\ \frac \operatorname z = -\bigl(1 + \operatorname^2 z\bigr)\operatornamez,\ \operatorname 0 = 0,\ \operatorname 0 = 1,$

or equivalently as the inverses of an elliptic integral, the Schwarz–Christoffel map from the complex unit disk to a square with corners $\big\\colon$
:$z = \int_0^\frac = \int_^1\frac.$

Beyond that square, the functions can be analytically continued to the whole complex plane by a series of reflections.

By comparison, the circular sine and cosine can be defined as the solution to the initial value problem:

:$\frac \sin z = \cos z,\ \frac \cos z = -\sin z,\ \sin 0 = 0,\ \cos 0 = 1,$

or as inverses of a map from the upper half-plane to a half-infinite strip with real part between $-\tfrac12\pi, \tfrac12\pi$ and positive imaginary part:
:$z = \int_0^\frac = \int_^1\frac.$

Arc length of Bernoulli's lemniscate

The lemniscate of Bernoulli with half-width is the locus of points in the plane such that the product of their distances from the two focal points $F_1 = \bigl(,0\bigr)$ and $F_2 = \bigl(\tfrac1\sqrt2,0\bigr)$ is the constant $\tfrac12$. This is a quartic curve satisfying the polar equation $r^2 = \cos 2\theta$ or the Cartesian equation $\bigl(x^2+y^2\bigr)^2=x^2-y^2.$

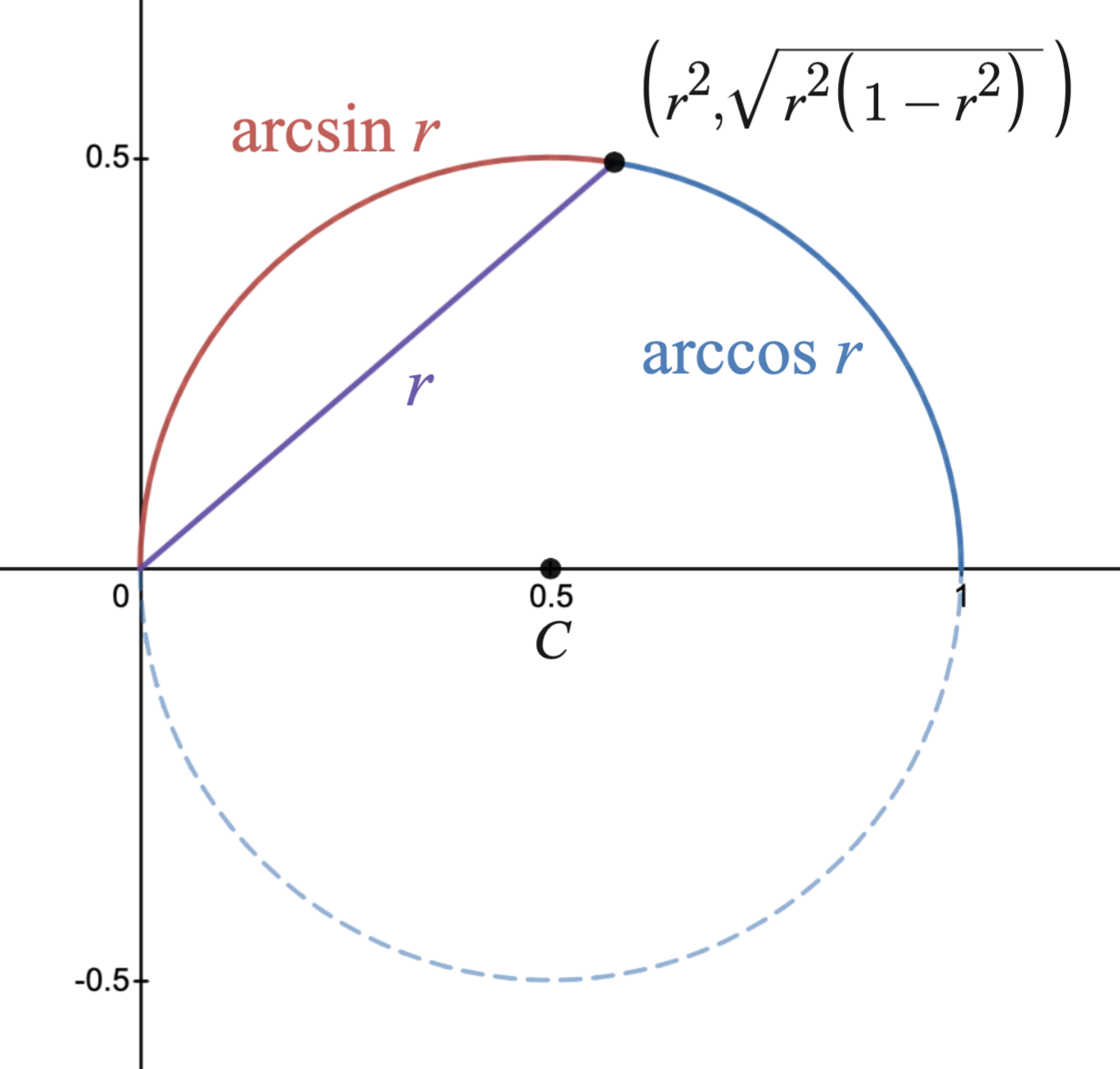
The points on the lemniscate at distance $r$ from the origin are the intersections of the circle $x^2+y^2=r^2$ and the hyperbola $x^2-y^2=r^4$. The intersection in the positive quadrant has Cartesian coordinates:
:$\big(x(r), y(r)\big) = \biggl(\!\sqrt,\, \sqrt\,\biggr).$

Using this parametrization with $r \in$, 1/math> for a quarter of the lemniscate, the arc length from the origin to a point $\big(x(r), y(r)\big)$ is:
:\begin
&\int_0^r \sqrt \mathop \\
& \quad = \int_0^r \sqrt \mathop \\ mu& \quad = \int_0^r \frac \\ mu& \quad = \operatorname r.
\end

Likewise, the arc length from $(1,0)$ to $\big(x(r), y(r)\big)$ is:
:\begin
&\int_r^1 \sqrt \mathop \\
& \quad = \int_r^1 \frac \\ mu& \quad = \operatorname r = \tfrac12\varpi - \operatorname r.
\end

Or in the inverse direction, the lemniscate sine and cosine functions give the distance from the origin as functions of arc length from the origin and the point $(1,0)$, respectively.

Analogously, the circular sine and cosine functions relate the chord length to the arc length for the unit diameter circle with polar equation $r = \cos \theta$ or Cartesian equation $x^2 + y^2 = x,$ using the same argument above but with the parametrization:
:$\big(x(r), y(r)\big) = \biggl(r^2,\, \sqrt\,\biggr).$

Alternatively, just as the unit circle $x^2+y^2=1$ is parametrized in terms of the arc length $s$ from the point $(1,0)$ by

:$(x(s),y(s))=(\cos s,\sin s),$

the lemniscate is parametrized in terms of the arc length $s$ from the point $(1,0)$ by

:$(x(s),y(s))=\left(\frac,\frac\right)=\left(\tilde\,s,\tilde\,s\right).$

The lemniscate integral and lemniscate functions satisfy an argument duplication identity discovered by Fagnano in 1718:

:$\int_0^z \frac = 2 \int_0^u \frac, \quad \text z = \frac \text 0\le u\le\sqrt.$

Later mathematicians generalized this result. Analogously to the constructible polygons in the circle, the lemniscate can be divided into sections of equal arc length using only straightedge and compass if and only if is of the form $n = 2^kp_1p_2\cdots p_m$ where is a non-negative integer and each (if any) is a distinct Fermat prime. The "if" part of the theorem was proved by Niels Abel in 1827–1828, and the "only if" part was proved by Michael Rosen in 1981. Equivalently, the lemniscate can be divided into sections of equal arc length using only straightedge and compass if and only if $\varphi (n)$ is a power of two (where $\varphi$ is Euler's totient function). The lemniscate is ''not'' assumed to be already drawn; the theorem refers to constructing the division points only.

Let $r_j=\operatorname\dfrac$. Then the -division points for the lemniscate $(x^2+y^2)^2=x^2-y^2$ are the points

:$\left(r_j\sqrt,\ (-1)^ \sqrt\right),\quad j\in\$

where $\lfloor\cdot\rfloor$ is the floor function. See below for some specific values of $\operatorname\dfrac$.

Arc length of rectangular elastica

The inverse lemniscate sine also describes the arc length relative to the coordinate of the rectangular elastica. This curve has coordinate and arc length:
:$y = \int_x^1 \frac,\quad s = \operatorname x = \int_0^x \frac$

The rectangular elastica solves a problem posed by Jacob Bernoulli, in 1691, to describe the shape of an idealized flexible rod fixed in a vertical orientation at the bottom end and pulled down by a weight from the far end until it has been bent horizontal. Bernoulli's proposed solution established Euler–Bernoulli beam theory, further developed by Euler in the 18th century.

Elliptic characterization

Let $C$ be a point on the ellipse $x^2+2y^2=1$ in the first quadrant and let $D$ be the projection of $C$ on the unit circle $x^2+y^2=1$. The distance $r$ between the origin $A$ and the point $C$ is a function of $\varphi$ (the angle $BAC$ where $B=(1,0)$; equivalently the length of the circular arc $BD$). The parameter $u$ is given by
:$u=\int_0^r(\theta)\, \mathrm d\theta=\int_0^\frac.$
If $E$ is the projection of $D$ on the x-axis and if $F$ is the projection of $C$ on the x-axis, then the lemniscate elliptic functions are given by
:$\operatornameu=\overline, \quad \operatornameu=\overline.$

Relation to the lemniscate constant

The lemniscate functions have minimal real period and fundamental complex periods $(1+i)\varpi$ and $(1-i)\varpi$ for a constant called the ''lemniscate constant'',

:$\varpi = 2\int_0^1\frac = 2.62205\ldots$

The lemniscate functions satisfy the basic relation $\operatornamez = \bigl(\tfrac12\varpi - z\bigr),$ analogous to the relation $\cos z = \bigl(\tfrac12\pi - z\bigr).$

The lemniscate constant is a close analog of the circle constant , and many identities involving have analogues involving , as identities involving the trigonometric functions have analogues involving the lemniscate functions. For example, Viète's formula for can be written:

$\frac2\pi = \sqrt\frac12 \cdot \sqrt \cdot \sqrt \cdots$

An analogous formula for is:

$\frac2\varpi = \sqrt\frac12 \cdot \sqrt \cdot \sqrt \cdots$

The Machin formula for is $\tfrac14\pi = 4 \arctan \tfrac15 - \arctan \tfrac1,$ and several similar formulas for can be developed using trigonometric angle sum identities, e.g. Euler's formula $\tfrac14\pi = \arctan\tfrac12 + \arctan\tfrac13$. Analogous formulas can be developed for , including the following found by Gauss: $\tfrac12\varpi = 2 \operatorname \tfrac12 + \operatorname \tfrac7.$

The lemniscate and circle constants were found by Gauss to be related to each-other by the arithmetic-geometric mean :

$\frac\pi\varpi = M$

Zeros, poles and symmetries

The lemniscate functions and are even and odd functions, respectively,
:\begin
\operatorname(-z) &= \operatorname z \\ mu\operatorname(-z) &= - \operatorname z
\end

At translations of $\tfrac12\varpi,$ and are exchanged, and at translations of $\tfrac12i\varpi$ they are additionally rotated and reciprocated:

:\begin
\bigl(z \pm \tfrac12\varpi\bigr) &= \mp\operatorname z,&
\bigl(z \pm \tfrac12i\varpi\bigr) &= \frac \\ mu\bigl(z \pm \tfrac12\varpi\bigr) &= \pm\operatorname z,&
\bigl(z \pm \tfrac12i\varpi\bigr) &= \frac
\end

Doubling these to translations by a unit-Gaussian-integer multiple of $\varpi$ (that is, $\pm \varpi$ or $\pm i\varpi$), negates each function, an involution:

:\begin
\operatorname (z + \varpi) &= \operatorname (z + i\varpi) = -\operatorname z \\ mu\operatorname (z + \varpi) &= \operatorname (z + i\varpi) = -\operatorname z
\end

As a result, both functions are invariant under translation by an even-Gaussian-integer multiple of $\varpi$. That is, a displacement $(a + bi)\varpi,$ with $a + b = 2k$ for integers , , and .

:\begin
\bigl(z + (1 + i)\varpi\bigr) &= \bigl(z + (1 - i)\varpi\bigr) = \operatorname z \\ mu\bigl(z + (1 + i)\varpi\bigr) &= \bigl(z + (1 - i)\varpi\bigr) = \operatorname z
\end

This makes them elliptic functions (doubly periodic meromorphic functions in the complex plane) with a diagonal square period lattice of fundamental periods $(1 + i)\varpi$ and $(1 - i)\varpi$. Elliptic functions with a square period lattice are more symmetrical than arbitrary elliptic functions, following the symmetries of the square.

Reflections and quarter-turn rotations of lemniscate function arguments have simple expressions:

:\begin
\operatorname \bar &= \overline \\ mu\operatorname \bar &= \overline \\ mu\operatorname iz &= \frac \\ mu\operatorname iz &= i \operatorname z
\end

The function has simple zeros at Gaussian integer multiples of , complex numbers of the form $a\varpi + b\varpi i$ for integers and . It has simple poles at Gaussian half-integer multiples of , complex numbers of the form $\bigl(a + \tfrac12\bigr)\varpi + \bigl(b + \tfrac12\bigr)\varpi i$, with residues $(-1)^i$. The function is reflected and offset from the function, $\operatornamez = \bigl(\tfrac12\varpi - z\bigr)$. It has zeros for arguments $\bigl(a + \tfrac12\bigr)\varpi + b\varpi i$ and poles for arguments $a\varpi + \bigl(b + \tfrac12\bigr)\varpi i,$ with residues $(-1)^i.$

Also
:$\operatornamez=\operatornamew\leftrightarrow z=(-1)^w+(m+ni)\varpi$
for some $m,n\in\mathbb$ and
:$\operatorname((1\pm i)z)=(1\pm i)\frac.$
The last formula is a special case of complex multiplication. Analogous formulas can be given for $\operatorname((n+mi)z)$ where $n+mi$ is any Gaussian integer – the function $\operatorname$ has complex multiplication by \mathbb /math>.

Since the lemniscate sine is a meromorphic function in the whole complex plane, it can be written as a ratio of entire functions. Gauss showed that has the following product expansion, reflecting the distribution of its zeros and poles:

:$\operatornamez=\frac$

where

:$M(z)=z\prod_\left(1-\frac\right),\quad N(z)=\prod_\left(1-\frac\right).$

Here, $\alpha$ and $\beta$ denote, respectively, the zeros and poles of which are in the quadrant $\operatornamez>0,\operatornamez\ge 0$. Gauss conjectured that $\ln N(\varpi)=\pi/2$ (this later turned out to be true) and commented that this “is most remarkable and a proof of this property promises the most serious increase in analysis”. Gauss expanded the products for $M$ and $N$ as infinite series. He also discovered several identities involving the functions $M$ and $N$, such as
:$N(z)=\frac,$
:$N(2z)=M^4(z)+N^4(z)$
and
:$M(2z)=2M(z)N(z)N((1+i)z).$

Since the functions $M$ and $N$ are entire, their power series expansions converge everywhere in the complex plane:
:$M(z)=z-2\frac-36\frac+552\frac+\cdots,\quad z\in\mathbb$
:$N(z)=1+2\frac-4\frac+408\frac+\cdots,\quad z\in\mathbb.$

There are also infinite series reflecting the distribution of the zeros and poles of :
:$\frac=\sum_\frac$
:$\operatornamez=-i\sum_\frac.$

Pythagorean-like identity

The lemniscate functions satisfy a Pythagorean-like identity:
:$\operatorname z + \operatorname z + \operatorname z \, \operatorname z = 1$

As a result, the parametric equation $(x, y) = (\operatorname t, \operatorname t)$ parametrizes the quartic curve $x^2 + y^2 + x^2y^2 = 1.$

This identity can alternately be rewritten:

:$\bigl(1 + \operatorname z\bigr) \bigl(1+\operatorname z\bigr) = 2$

:$\operatorname z = \frac,\quad \operatorname z = \frac$

Defining a tangent-sum operator as $a \oplus b \mathrel \tan(\arctan a + \arctan b),$ gives:

:$\operatorname z \oplus \operatorname z = 1$

Derivatives and integrals

The derivatives are as follows:

:\begin
\frac\operatorname z = \operatornamez
&= -\bigl(1 + \operatorname z\bigr)\operatornamez=-\frac \\
\operatorname z &= 1 - \operatorname z \\ mu
\frac\operatorname z = \operatornamez
&= \bigl(1 + \operatorname z\bigr)\operatornamez=\frac\\
\operatorname z &= 1 - \operatorname z

\end

The second derivatives of lemniscate sine and lemniscate cosine are their negative duplicated cubes:

:$\frac\operatornamez = -2\operatornamez$

:$\frac\operatornamez = -2\operatornamez$

The lemniscate functions can be integrated using the inverse tangent function:

:$\int\operatorname z \mathop = \arctan \operatorname z + C$

:$\int\operatorname z \mathop = -\arctan \operatorname z + C$

Argument sum and multiple identities

Like the trigonometric functions, the lemniscate functions satisfy argument sum and difference identities. The original identity used by Fagnano for bisection of the lemniscate was:

: $\operatorname(u+v) = \frac$

The derivative and Pythagorean-like identities can be used to rework the identity used by Fagano in terms of and . Defining a tangent-sum operator $a \oplus b \mathrel \tan(\arctan a + \arctan b)$ and tangent-difference operator $a \ominus b \mathrel a \oplus (-b),$ the argument sum and difference identities can be expressed as:

:\begin
\operatorname(u+v)
&= \operatornameu\,\operatornamev \ominus \operatornameu\, \operatornamev
= \frac
\\ mu\operatorname(u-v)
&= \operatornameu\,\operatornamev \oplus \operatornameu\, \operatornamev \\ mu\operatorname(u+v)
&= \operatornameu\,\operatornamev \oplus \operatornameu\,\operatornamev
= \frac
\\ mu\operatorname(u-v)
&= \operatornameu\,\operatornamev \ominus \operatornameu\,\operatornamev
\end

These resemble their trigonometric analogs:

:\begin
\cos(u \pm v) &= \cos u\,\cos v \mp \sin u\,\sin v \\ mu\sin(u \pm v) &= \sin u\,\cos v \pm \cos u\,\sin v
\end

In particular, to compute the complex-valued functions in real components,

:\begin
\operatorname(x + iy)
&= \frac
\\ mu&= \frac
- i \frac
\\ 2mu\operatorname(x + iy)
&= \frac
\\ mu&= \frac
+ i \frac
\end

Bisection formulas:

:$\operatorname^2 \tfrac12x = \frac$

:$\operatorname^2 \tfrac12x = \frac$

Duplication formulas:§46 p. 80
/ref>

:$\operatorname 2x = \frac$

:$\operatorname 2x = 2\,\operatornamex\,\operatornamex\frac$

Triplication formulas:

:$\operatorname 3x = \frac$

:$\operatorname 3x = \frac$

Note the "reverse symmetry" of the coefficients of numerator and denominator of $\operatorname3x$. This phenomenon can be observed in multiplication formulas for $\operatorname\beta x$ where $\beta=m+ni$ whenever $m,n\in\mathbb$ and $m+n$ is odd.

Lemnatomic polynomials

Let $L$ be the lattice
:$L=\mathbb(1+i)\varpi +\mathbb(1-i)\varpi.$
Furthermore, let $K=\mathbb(i)$, \mathcal=\mathbb /math>, $z\in\mathbb$, $\beta=m+in$, $\gamma=m'+in'$ (where $m,n,m',n'\in\mathbb$), $m+n$ be odd, $m'+n'$ be odd, $\gamma\equiv 1\,\operatorname\, 2(1+i)$ and $\operatorname \beta z=M_\beta (\operatornamez)$. Then
:$M_\beta (x)=i^\varepsilon x \frac$
for some coprime polynomials P_\beta (x), Q_\beta (x)\in \mathcal /math>
and some $\varepsilon\in \$ where
:$xP_\beta (x^4)=\prod_\Lambda_\gamma (x)$
and
:$\Lambda_\beta (x)=\prod_(x-\operatorname\alpha\delta_\beta)$
where $\delta_\beta$ is any $\beta$-torsion generator (i.e. $\delta_\beta \in (1/\beta)L$ and delta_\betain (1/\beta)L/L generates $(1/\beta)L/L$ as an $\mathcal$-module). Examples of $\beta$-torsion generators include $2\varpi/\beta$ and $(1+i)\varpi/\beta$. The polynomial \Lambda_\beta (x)\in\mathcal /math> is called the $\beta$-th lemnatomic polynomial. It is monic and is irreducible over $K$. The lemnatomic polynomials are the "lemniscate analogs" of the cyclotomic polynomials,
:$\Phi_k(x)=\prod_(x-\zeta_k^a).$

The $\beta$-th lemnatomic polynomial $\Lambda_\beta(x)$ is the minimal polynomial of $\operatorname\delta_\beta$ in K /math>. For convenience, let $\omega_=\operatorname(2\varpi/\beta)$ and $\tilde_=\operatorname((1+i)\varpi/\beta)$. So for example, the minimal polynomial of $\omega_5$ (and also of $\tilde_5$) in K /math> is
:$\Lambda_5(x)=x^+52x^-26x^8-12x^4+1,$
and
:\omega_5=\sqrt /math>
:\tilde_5=\sqrt /math>The fourth root with the least positive principal argument is chosen.
(an equivalent expression is given in the table below). Another example is
:$\Lambda_(x)=x^4-1+2i$
which is the minimal polynomial of $\omega_$ (and also of $\tilde_$) in K

If $p$ is prime and $\beta$ is positive and odd, then
:$\operatorname\Lambda_=\beta^2\prod_\left(1-\frac\right)\left(1-\frac\right)$
which can be compared to the cyclotomic analog
:$\operatorname\Phi_=k\prod_\left(1-\frac\right).$

Specific values

Just as for the trigonometric functions, values of the lemniscate functions can be computed for divisions of the lemniscate into parts of equal length, using only basic arithmetic and square roots, if and only if is of the form $n = 2^kp_1p_2\cdots p_m$ where is a non-negative integer and each (if any) is a distinct Fermat prime. The expressions become unwieldy as grows. Below are the expressions for dividing the lemniscate $(x^2+y^2)^2=x^2-y^2$ into parts of equal length for some .

Power series

The power series expansion of the lemniscate sine at the origin is
:$\operatornamez=\sum_^\infty a_n z^n=z-12\frac+3024\frac-4390848\frac+\cdots,\quad , z, < \tfrac$
where the coefficients $a_n$ are determined as follows:
:$n\not\equiv 1\pmod 4\implies a_n=0,$
:$a_1=1,\, \forall n\in\mathbb_0:\,a_=-\frac\sum_a_ia_ja_k$

where $i+j+k=n$ stands for all three-term compositions of $n$. For example, to evaluate $a_$, it can be seen that there are only six compositions of $13-2=11$ that give a nonzero contribution to the sum: $11=9+1+1=1+9+1=1+1+9$ and $11=5+5+1=5+1+5=1+5+5$, so
:$a_=-\tfrac(a_9a_1a_1+a_1a_9a_1+a_1a_1a_9+a_5a_5a_1+a_5a_1a_5+a_1a_5a_5)=-\tfrac.$

The expansion can be equivalently written as
:$\operatornamez=\sum_^\infty p_ \frac,\quad \left, z\<\frac$
where
:$p_=-12\sum_^n\binomp_\sum_^j \binomp_k p_,\quad p_0=1,\, p_1=0.$

The power series expansion of $\tilde$ at the origin is
:$\tilde\,z=\sum_^\infty \alpha_n z^n=z-9\frac+153\frac-4977\frac+\cdots,\quad \left, z\<\frac$
where $\alpha_n=0$ if $n$ is even and
:$\alpha_n=\sqrt\frac\frac\sum_^\frac,\quad \left, \alpha_n\\sim 2^\frac$
if $n$ is odd.

The expansion can be equivalently written as
:$\tilde\, z=\sum_^\infty \frac \left(\sum_^n 2^l \binom s_l t_\right)\frac ,\quad \left, z\<\frac$
where
:$s_=3 s_ +24 \sum_^n \binom s_ \sum_^j \binom s_k s_,\quad s_0=1,\, s_1=3,$
:$t_=3 t_+3 \sum_^n \binom t_ \sum_^j \binom t_k t_,\quad t_0=1,\, t_1=3.$

For the lemniscate cosine,
:$\operatorname=1-\sum_^\infty (-1)^n \left(\sum_^n 2^l \binom q_l r_\right) \frac=1-2\frac+12\frac-216\frac+\cdots ,\quad \left, z\<\frac,$
:$\tilde\,z=\sum_^\infty (-1)^n 2^n q_n \frac=1-3\frac+33\frac-819\frac+\cdots ,\quad\left, z\<\frac$
where
:$r_=3 \sum_^n \binom r_ \sum_^j \binom r_k r_,\quad r_0=1,\, r_1=0,$
:$q_=\tfrac q_+6 \sum_^n \binom q_ \sum_^j \binom q_k q_,\quad q_0=1, \,q_1=\tfrac.$

Relation to Weierstrass and Jacobi elliptic functions

The lemniscate functions are closely related to the Weierstrass elliptic function $\wp(z; 1, 0)$ (the "lemniscatic case"), with invariants and . This lattice has fundamental periods $\omega_1 = \sqrt\varpi,$ and $\omega_2 = i\omega_1$. The associated constants of the Weierstrass function are $e_1=\tfrac12,\ e_2=0,\ e_3=-\tfrac12.$

The related case of a Weierstrass elliptic function with , may be handled by a scaling transformation. However, this may involve complex numbers. If it is desired to remain within real numbers, there are two cases to consider: and . The period parallelogram is either a square or a rhombus. The Weierstrass elliptic function $\wp (z;-1,0)$ is called the "pseudolemniscatic case".

The square of the lemniscate sine can be represented as

:$\operatorname^2 z=\frac=\frac=$

where the second and third argument of $\wp$ denote the lattice invariants and . Another representation is
:$\operatorname^2z=\frac$
where the second argument of $\weierp$ denotes the period ratio $\tau$. The lemniscate sine is a rational function in the Weierstrass elliptic function and its derivative:
:$\operatornamez=-2\frac$
where the second and third argument of $\wp$ denote the lattice invariants and . In terms of the period ratio $\tau$, this becomes
:$\operatornamez=-2\frac.$

The lemniscate functions can also be written in terms of Jacobi elliptic functions. The Jacobi elliptic functions $\operatorname$ and $\operatorname$ with positive real elliptic modulus have an "upright" rectangular lattice aligned with real and imaginary axes. Alternately, the functions $\operatorname$ and $\operatorname$ with modulus (and $\operatorname$ and $\operatorname$ with modulus $1/\sqrt$) have a square period lattice rotated 1/8 turn.

:$\operatorname z = \operatorname(z;i)=\left(\sqrt2z;\tfrac\right)$

:$\operatorname z = \operatorname(z;i)= \left(\sqrt2z;\tfrac\right)$

where the second arguments denote the elliptic modulus $k$.

Yet another representation of $\operatorname$, in terms of the Jacobi elliptic function $\operatorname$, is

:$\operatornamez=\operatorname(z;\sqrt)$

where the second argument of $\operatorname$ denotes the elliptic modulus $k$.

The functions $\tilde$ and $\tilde$ can also be expressed in terms of Jacobi elliptic functions:
:$\tilde\,z=\tfrac\operatorname\left(\sqrtz;\tfrac\right)\operatorname\left(\sqrtz;\tfrac\right),$
:$\tilde\,z=\operatorname\left(\sqrtz;\tfrac\right)\operatorname\left(\sqrtz;\tfrac\right).$

Relation to the modular lambda function

The lemniscate sine can be used for the computation of values of the modular lambda function:

:
\prod_^n \;
=\sqrt /math>

For example:

:\begin
&\bigl(\tfrac1\varpi\bigr)\,\bigl(\tfrac3\varpi\bigr)\,\bigl(\tfrac5\varpi\bigr) \\ mu&\quad = \sqrt
= \Bigl(\Bigl(\tfrac\sqrt+\tfrac\sqrt+1\Bigr)\Bigr)
\\ 8mu& \bigl(\tfrac1\varpi\bigr)\, \bigl(\tfrac3\varpi\bigr)\,\bigl(\tfrac5\varpi\bigr)\,\bigl(\tfrac7\varpi\bigr) \\ 3mu&\quad = \sqrt = \Biggl( \frac\pi4 - \Biggl(\frac\Biggr)\Biggr)
\end

Ramanujan's cos/cosh identity

Ramanujan's famous cos/cosh identity states that if
:$R(s)=\frac\sum_\frac,$
then
:$R(s)^+R(is)^=2,\quad \left, \operatornames\< \frac,\left, \operatornames\< \frac.$
There is a close relation between the lemniscate functions and $R(s)$. Indeed,
:$\tilde\,s=-\fracR(s)\quad \left, \operatornames\<\frac$
:$\tilde\,s=\frac\sqrt,\quad \left, \operatornames-\frac\<\frac,\,\left, \operatornames\<\frac$
and
:$R(s)=\frac,\quad \left, \operatornames\right , <\frac.$

Continued fractions

For $z\in\mathbb\setminus\$:
:$\int_0^\infty e^\operatornamet\, \mathrm dt=\cfrac,\quad a_n=\frac((-1)^+3)$
:$\int_0^\infty e^\operatornamet\operatornamet \, \mathrm dt=\cfrac,\quad a_n=n^2(4n^2-1),\, b_n=3(2n-1)^2$

Methods of computation

Several methods of computing $\operatorname x$ involve first making the change of variables $\pi x = \varpi \tilde$ and then computing $\operatorname(\varpi \tilde / \pi).$

A hyperbolic series method:

:$\operatorname\left(\fracx\right)=\frac\sum_ \frac,\quad x\in\mathbb$

:$\frac = \frac\pi\varpi \sum_\frac=\frac\pi\varpi \sum_\frac,\quad x\in\mathbb$

Fourier series method:
:$\operatorname\Bigl(\fracx\Bigr)=\frac\sum_^\infty \frac,\quad \left, \operatornamex\<\frac$
:$\operatorname\left(\fracx\right)=\frac\sum_^\infty \frac,\quad\left, \operatornamex\<\frac$
:$\frac=\frac\left(\frac-4\sum_^\infty \frac\right),\quad\left, \operatornamex\<\pi$

The lemniscate functions can be computed more rapidly by

:$\begin\operatorname\Bigl(\frac\varpi\pi x\Bigr)& = \frac,\quad x\in\mathbb\\ \operatorname\Bigl(\frac\varpi\pi x\Bigr)&=\frac,\quad x\in\mathbb\end$
where

:$\begin \theta_1(x,e^)&=\sum_(-1)^e^=\sum_ (-1)^n e^\sin ((2n+1)x),\\ \theta_2(x,e^)&=\sum_(-1)^n e^=\sum_ e^\cos ((2n+1)x),\\ \theta_3(x,e^)&=\sum_e^=\sum_ e^\cos 2nx,\\ \theta_4(x,e^)&=\sum_e^=\sum_ (-1)^n e^\cos 2nx\end$

are the Jacobi theta functions.

Two other fast computation methods use the following sum and product series:

:$\text\Bigl(\frac\varpi\pi x\Bigr) = f\biggl(\frac\varpi\sin x\sum_^ \frac\biggr)$
:$\text\Bigl(\frac\varpi\pi x\Bigr) = f\biggl(\frac\varpi\cos x\sum_^ \frac\biggr)$
:$\mathrm\Bigl(\frac\varpi\pi x\Bigr) = 2e^\sin x\prod_^ \frac,\quad x\in\mathbb$
:$\mathrm\Bigl(\frac\varpi\pi x\Bigr) = 2e^\cos x\prod_^ \frac,\quad x\in\mathbb$

where $f(x) = \tan(2 \arctan x) = 2x / (1 - x^2).$

Fourier series for the logarithm of the lemniscate sine:

:$\ln \operatorname\left(\frac\varpi\pi x\right)=\ln 2-\frac+\ln\sin x+2\sum_^\infty \frac,\quad \left, \operatornamex\<\frac$

The following series identities were discovered by Ramanujan:

:$\frac=\frac-\frac-8\sum_^\infty \frac,\quad \left, \operatornamex\<\pi$
:$\arctan\operatorname\Bigl(\frac\varpi\pi x\Bigr)=2\sum_^\infty \frac,\quad \left, \operatornamex\<\frac$

The functions $\tilde$ and $\tilde$ analogous to $\sin$ and $\cos$ on the unit circle have the following Fourier and hyperbolic series expansions:

:$\tilde\,s=2\sqrt\frac\sum_^\infty\frac,\quad \left, \operatornames\<\frac$
:$\tilde\,s=\sqrt\frac\sum_^\infty \frac,\quad \left, \operatornames\<\frac$
:$\tilde\,s=\frac\sum_\frac,\quad s\in\mathbb$
:$\tilde\,s=\frac\sum_\frac,\quad s\in\mathbb$

Inverse functions

The inverse function of the lemniscate sine is the lemniscate arcsine, defined as

:$\operatorname x = \int_0^x \frac.$

It can also be represented by the hypergeometric function:

:$\operatornamex=x\,_2F_1\left(\tfrac12,\tfrac14;\tfrac54;x^4\right).$

The inverse function of the lemniscate cosine is the lemniscate arccosine. This function is defined by following expression:

:$\operatorname x = \int_^ \frac = \tfrac12\varpi - \operatornamex$

For in the interval $-1 \leq x \leq 1$, $\operatorname\operatorname x = x$ and $\operatorname\operatorname x = x$

For the halving of the lemniscate arc length these formulas are valid:

:$\begin \bigl(\tfrac12\operatorname x\bigr) &= \bigl(\tfrac12\arcsin x\bigr) \,\bigl(\tfrac12\operatorname x\bigr) \\ \bigl(\tfrac12\operatorname x\bigr)^2 &= \bigl(\tfrac14\arcsin x^2\bigr) \end$

Expression using elliptic integrals

The lemniscate arcsine and the lemniscate arccosine can also be expressed by the Legendre-Form:

These functions can be displayed directly by using the incomplete elliptic integral of the first kind:

:$\operatorname x = \fracF\left(;\frac\right)$

:$\operatorname x = 2(\sqrt2-1)F\left(;(\sqrt2-1)^2\right)$

The arc lengths of the lemniscate can also be expressed by only using the arc lengths of ellipses (calculated by elliptic integrals of the second kind):

:\begin
\operatorname x = &\fracE\left(;(\sqrt2-1)^2\right) \\ mu&\ \ - E\left(;\frac\right) + \frac
\end

The lemniscate arccosine has this expression:

:$\operatorname x = \fracF\left(\arccos x;\frac\right)$

Use in integration

The lemniscate arcsine can be used to integrate many functions. Here is a list of important integrals (the constants of integration are omitted):

:$\int\frac\,\mathrm dx=\operatorname x$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\frac\,\mathrm dx=$

:$\int\sqrt\,\mathrm dx=\tanh \tfrac12x$

:$\int\sqrt\,\mathrm dx=\tan \tfrac12x$

Hyperbolic lemniscate functions

For convenience, let $\sigma=\sqrt\varpi$. $\sigma$ is the "squircular" analog of $\pi$ (see below). The decimal expansion of $\sigma$ (i.e. $3.7081\ldots$) appears in entry 34e of chapter 11 of Ramanujan's second notebook.

The hyperbolic lemniscate sine () and cosine () can be defined as inverses of elliptic integrals as follows:

:$z \mathrel \int_0^ \frac = \int_^\infty \frac$

where in $(*)$, $z$ is in the square with corners $\$. Beyond that square, the functions can be analytically continued to meromorphic functions in the whole complex plane.

The complete integral has the value:

:$\int_0^\infty \frac = \tfrac14 \Beta\bigl(\tfrac14, \tfrac14\bigr) = \frac = 1.85407\;46773\;01371\ldots$

Therefore, the two defined functions have following relation to each other:

:$\operatorname z =$

The product of hyperbolic lemniscate sine and hyperbolic lemniscate cosine is equal to one:

:$\operatornamez\,\operatornamez = 1$

The functions $\operatorname$ and $\operatorname$ have a square period lattice with fundamental periods $\$.

The hyperbolic lemniscate functions can be expressed in terms of lemniscate sine and lemniscate cosine:

:$\operatorname\bigl(\sqrt2 z\bigr) = \frac$

:$\operatorname\bigl(\sqrt2 z\bigr) = \frac$

But there is also a relation to the Jacobi elliptic functions with the elliptic modulus one by square root of two:

:$\operatornamez = \frac$

:$\operatornamez = \frac$

The hyperbolic lemniscate sine has following imaginary relation to the lemniscate sine:

:$\operatornamez = \frac \operatorname\left(\fracz\right) = \frac$

This is analogous to the relationship between hyperbolic and trigonometric sine:

:$\sinh z = -i \sin (iz) = \frac$

In a quartic Fermat curve $x^4 + y^4 = 1$ (sometimes called a squircle) the hyperbolic lemniscate sine and cosine are analogous to the tangent and cotangent functions in a unit circle $x^2 + y^2 = 1$ (the quadratic Fermat curve). If the origin and a point on the curve are connected to each other by a line , the hyperbolic lemniscate sine of twice the enclosed area between this line and the x-axis is the y-coordinate of the intersection of with the line $x = 1$. Just as $\pi$ is the area enclosed by the circle $x^2+y^2=1$, the area enclosed by the squircle $x^4+y^4=1$ is $\sigma$. Moreover,

:$M(1,1/\sqrt)=\frac$

where $M$ is the arithmetic–geometric mean.

The hyperbolic lemniscate sine satisfies the argument addition identity:

:$\operatorname(a+b) = \frac$

When $x$ is real, the derivative can be expressed in this way:

:$\frac\operatornamex = \sqrt.$

Number theory

In algebraic number theory, every finite abelian extension of the Gaussian rationals $\mathbb(i)$ is a subfield of $\mathbb(i,\omega_n)$ for some positive integer $n$. p. 508, 509 This is analogous to the Kronecker–Weber theorem for the rational numbers $\mathbb$ which is based on division of the circle – in particular, every finite abelian extension of $\mathbb$ is a subfield of $\mathbb(\zeta_n)$ for some positive integer $n$. Both are special cases of Kronecker's Jugendtraum, which became Hilbert's twelfth problem.

The field $\mathbb(i,\operatorname(\varpi /n))$ (for positive odd $n$) is the extension of $\mathbb(i)$ generated by the $x$- and $y$-coordinates of the $(1+i)n$- torsion points on the elliptic curve $y^2=4x^3+x$.

Hurwitz numbers

The Bernoulli numbers $\mathrm_n$ can be defined by
:$\mathrm_n=\lim_\frac\frac=\lim_\frac\frac\coth\frac,\quad n\ge 2$
and appear in
:$\sum_\frac=(-1)^\mathrm_\frac=2\zeta (2n),\quad n\ge 1$
where $\zeta$ is the Riemann zeta function.

The Hurwitz numbers p. 203—206 $\mathrm_n$ are the "lemniscate analogs" of the Bernoulli numbers. They can be defined by
:$\mathrm_n=-\lim_\frac\left(\frac\frac+\frac\mathcal\left(\frac;i\right)\right), \quad n\ge 4$
and appear in
:$\sum_\frac=\mathrm_\frac=G_(i),\quad n\ge 1$
where $\mathcal(z;i)$ is the Jacobi epsilon function with modulus $i$, \mathbb /math> are the Gaussian integers and $G_$ are the Eisenstein series of weight $4n$.

The Hurwitz numbers can also be determined as follows: $\mathrm_4=1/10$,
:$\mathrm_=\frac\sum_^\binom(4k-1)(4(n-k)-1)\mathrm_\mathrm_,\quad n\ge 2$
and $\mathrm_n=0$ if $n$ is not a multiple of $4$. This yields
:$\mathrm_8=\frac,\,\mathrm_=\frac,\,\mathrm_=\frac,\,\ldots$

Just as the denominator of $\mathrm_$ is the product of all primes $p$ such that $p-1$ divides $2n$ (by the von Staudt–Clausen theorem), the denominator of $\mathrm_$ is the product of $2$ and the primes of the form $p\equiv 1\, (\operatorname4)$ such that $p-1$ divides $4n$.

In fact, the von Staudt–Clausen theorem states that
:$\mathrm_+\sum_\frac\in\mathbb,\quad n\ge 1$
where $p$ is any prime, and an analogous theorem holds for the Hurwitz numbers: suppose that $a\in\mathbb$ is odd, $b\in\mathbb$ is even, $p$ is a prime such that $p\equiv 1\,(\mathrm\,4)$, $p=a^2+b^2$ (see Fermat's theorem on sums of two squares) and $a\equiv b+1\,(\mathrm\,4)$. Then for any given $p$, $a=a_p$ is uniquely determined and
:$\mathrm_-\frac-\sum_\frac\mathrel\mathrm_n\in\mathbb,\quad n\ge 1.$
The sequence of the integers $\mathrm_n$ starts with $0,-1,5,253,\ldots .$

Let $n\ge 2$. If $4n+1$ is a prime, then $\mathrm_n\equiv 1\,(\mathrm\,4)$. If $4n+1$ is not a prime, then $\mathrm_n\equiv 3\,(\mathrm\,4)$.

Some authors instead define the Hurwitz numbers as $\mathrm_n'=\mathrm_$.

World map projections

The Peirce quincuncial projection, designed by Charles Sanders Peirce of the US Coast Survey in the 1870s, is a world map projection based on the inverse lemniscate sine of stereographically projected points (treated as complex numbers).

When lines of constant real or imaginary part are projected onto the complex plane via the hyperbolic lemniscate sine, and thence stereographically projected onto the sphere (see Riemann sphere), the resulting curves are spherical conics, the spherical analog of planar ellipses and hyperbolas. Thus the lemniscate functions (and more generally, the Jacobi elliptic functions) provide a parametrization for spherical conics.

A conformal map projection from the globe onto the 6 square faces of a cube can also be defined using the lemniscate functions. Because many partial differential equations can be effectively solved by conformal mapping, this map from sphere to cube is convenient for atmospheric modeling.; .

See also

* Elliptic function
** Abel elliptic functions
** Dixon elliptic functions
** Jacobi elliptic functions
** Weierstrass elliptic function
* Elliptic Gauss sum
* Gauss's constant
* Peirce quincuncial projection
* Schwarz–Christoffel mapping

Notes

External links

*

References

* Abel, Niels Henrik (1827–1828) "Recherches sur les fonctions elliptiques" esearch on elliptic functions(in French). ''Crelle's Journal''.Part 1
1827. 2 (2): 101–181. doibr>10.1515/crll.1827.2.101
Part 2
1828. 3 (3): 160–190. doibr>10.1515/crll.1828.3.160

*
*
*
*
*
*
*
*
*
*
*
* Leonhard Euler#Selected bibliography, E
252

Figures

*
605

*
* Giulio Carlo de' Toschi di Fagnano, Fagnano, Giulio Carlo (1718–1723) "Metodo per misurare la lemniscata" [Method for measuring the lemniscate]. ''Giornale de' letterati d'Italia'' (in Italian)."Schediasma primo"
art 1 1718. 29: 258–269."Giunte al primo schediasma"
ddendum to part 1 1723. 34: 197–207."Schediasma secondo"
art 2 1718. 30: 87–111.
Reprinted as
Figures

*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
*
* Sridharan, Ramaiyengar (2004) "Physics to Mathematics: from Lintearia to Lemniscate". ''Resonance''. "I"
9 (4): 21–29. doibr>10.1007/BF02834853
"II: Gauss and Landen's Work"
9 (6): 11–20. doibr>10.1007/BF02839214

*
*
*

{{bots, deny=Citation bot

Modular forms
Elliptic functions