Cell (mathematics)

In solid geometry, a face is a flat surface (a planar region) that forms part of the boundary of a solid object. For example, a cube has six faces in this sense.

In more modern treatments of the geometry of polyhedra and higher-dimensional polytopes, a "face" is defined in such a way that it may have any dimension. The vertices, edges, and (2-dimensional) faces of a polyhedron are all faces in this more general sense.

Polygonal face

In elementary geometry, a face is a polygon on the boundary of a polyhedron. (Here a "polygon" should be viewed as including the 2-dimensional region inside it.) Other names for a polygonal face include polyhedron side and Euclidean plane ''tile''.

For example, any of the six squares that bound a cube is a face of the cube. Sometimes "face" is also used to refer to the 2-dimensional features of a 4-polytope. With this meaning, the 4-dimensional tesseract has 24 square faces, each sharing two of 8 cubic cells.

Number of polygonal faces of a polyhedron

Any convex polyhedron's surface has Euler characteristic

:$V - E + F = 2,$

where is the number of vertices, is the number of edges, and is the number of faces. This equation is known as Euler's polyhedron formula. Thus the number of faces is 2 more than the excess of the number of edges over the number of vertices. For example, a cube has 12 edges and 8 vertices, and hence 6 faces.

''k''-face

In higher-dimensional geometry, the faces of a polytope are features of all dimensions. A face of dimension is sometimes called a -face. For example, the polygonal faces of an ordinary polyhedron are 2-faces. The word "face" is defined differently in different areas of mathematics. For example, many but not all authors allow the polytope itself and the empty set as faces of a polytope, where the empty set is for consistency given a "dimension" of −1. For any -dimensional polytope, faces have dimension $k$ with $-1 \leq k \leq n$.

For example, with this meaning, the faces of a cube comprise the cube itself (a 3-face), its (square) facets (2-faces), its (line segment) edges (1-faces), its (point) vertices (0-faces), and the empty set.

In some areas of mathematics, such as polyhedral combinatorics, a polytope is by definition convex. In this setting, there is a precise definition: a face of a polytope in Euclidean space $\mathbf^n$ is the intersection of with any closed halfspace whose boundary is disjoint from the relative interior of . According to this definition, the set of faces of a polytope includes the polytope itself and the empty set. For convex polytopes, this definition is equivalent to the general definition of a face of a convex set, given below.

In other areas of mathematics, such as the theories of abstract polytopes and star polytopes, the requirement of convexity is relaxed. One precise combinatorial concept that generalizes some earlier types of polyhedra is the notion of a simplicial complex. More generally, there is the notion of a polytopal complex.

An -dimensional simplex (line segment (), triangle (), tetrahedron (), etc.), defined by vertices, has a face for each subset of the vertices, from the empty set up through the set of all vertices. In particular, there are faces in total. The number of -faces, for , is the binomial coefficient $\binom$.

There are specific names for -faces depending on the value of and, in some cases, how close is to the dimension of the polytope.

Vertex or 0-face

Vertex is the common name for a 0-face.

Edge or 1-face

Edge is the common name for a 1-face.

Face or 2-face

The use of face in a context where a specific is meant for a -face but is not explicitly specified is commonly a 2-face.

Cell or 3-face

A cell is a polyhedral element (3-face) of a 4-dimensional polytope or 3-dimensional tessellation, or higher. Cells are facets for 4-polytopes and 3-honeycombs.

Examples:

Facet or (''n'' − 1)-face

In higher-dimensional geometry, the facets of a -polytope are the ()-faces (faces of dimension one less than the polytope itself). A polytope is bounded by its facets.

For example:
*The facets of a line segment are its 0-faces or vertices.
*The facets of a polygon are its 1-faces or edges.
*The facets of a polyhedron or plane tiling are its 2-faces.
*The facets of a 4D polytope or 3-honeycomb are its 3-faces or cells.
*The facets of a 5D polytope or 4-honeycomb are its 4-faces.

Ridge or (''n'' − 2)-face

In related terminology, the ()-''face''s of an -polytope are called ridges (also subfacets). A ridge is seen as the boundary between exactly two facets of a polytope or honeycomb.

For example:
*The ridges of a 2D polygon or 1D tiling are its 0-faces or vertices.
*The ridges of a 3D polyhedron or plane tiling are its 1-faces or edges.
*The ridges of a 4D polytope or 3-honeycomb are its 2-faces or simply faces.
*The ridges of a 5D polytope or 4-honeycomb are its 3-faces or cells.

Peak or (''n'' − 3)-face

The ()-''face''s of an -polytope are called peaks. A peak contains a rotational axis of facets and ridges in a regular polytope or honeycomb.

For example:
*The peaks of a 3D polyhedron or plane tiling are its 0-faces or vertices.
*The peaks of a 4D polytope or 3-honeycomb are its 1-faces or edges.
*The peaks of a 5D polytope or 4-honeycomb are its 2-faces or simply faces.

Face of a convex set

The notion of a face can be generalized from convex polytopes to all convex sets, as follows. Let $C$ be a convex set in a real vector space $V$. A face of $C$ is a convex subset $F\subseteq C$ such that whenever a point $p\in F$ lies strictly between two points $x$ and $y$ in $C$, both $x$ and $y$ must be in $F$. Equivalently, for any $x,y\in C$ and any real number $0<\theta<1$ such that $\theta x+(1-\theta)y$ is in $F$, $x$ and $y$ must be in $F$.

According to this definition, $C$ itself and the empty set are faces of $C$; these are sometimes called the ''trivial faces'' of $C$.

An extreme point of $C$ is a point $p\in C$ such that $\$ is a face of $C$. That is, if $p$ lies between two points $x,y\in C$, then $x=y=p$.

For example:
* A triangle in the plane (including the region inside) is a convex set. Its nontrivial faces are the three vertices and the three edges. (So the only extreme points are the three vertices.)
* The only nontrivial faces of the closed unit disk $\$ are its extreme points, namely the points on the unit circle $S^1 = \$.

Let $C$ be a convex set in $\R^n$ that is compact (or equivalently, closed and bounded). Then $C$ is the convex hull of its extreme points. More generally, each compact convex set in a locally convex topological vector space is the closed convex hull of its extreme points (the Krein–Milman theorem).

An exposed face of $C$ is the subset of points of $C$ where a linear functional achieves its minimum on $C$. Thus, if $f$ is a linear functional on $V$ and $\alpha =\inf\>-\infty$, then $\$ is an exposed face of $C$.

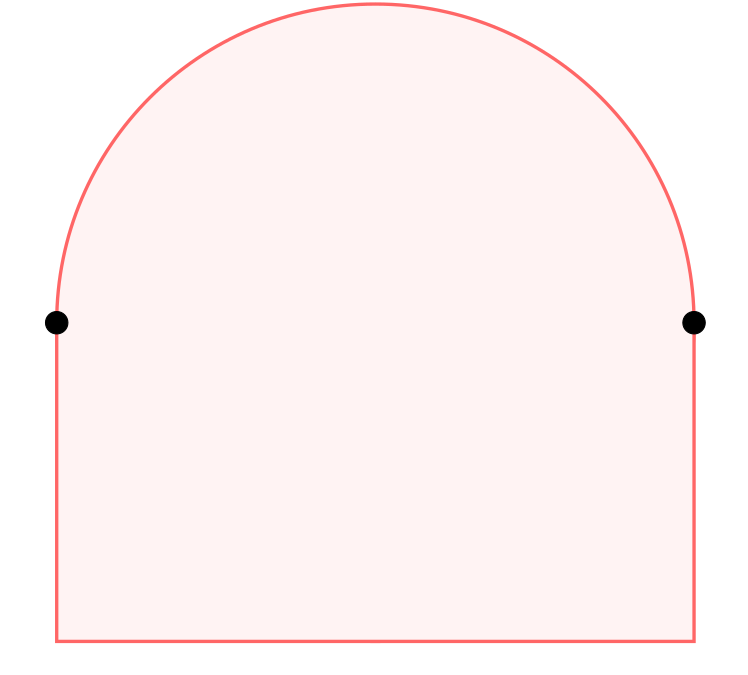
An exposed point of $C$ is a point $p\in C$ such that $\$ is an exposed face of $C$. That is, $f(p) > f(c)$ for all $c\in C\setminus\$. See the figure for examples of extreme points that are not exposed.

Competing definitions

Some authors do not include $C$ and/or $\varnothing$ as faces of $C$. Some authors require a face to be a closed subset; this is automatic for $C$ a compact convex set in a vector space of finite dimension, but not in infinite dimensions. In infinite dimensions, the functional $f$ is usually assumed to be continuous in a given vector topology.

Properties

An exposed face of a convex set is a face. In particular, it is a convex subset.

If $F$ is a face of a convex set $C$, then a subset $E\subseteq F$ is a face of $F$ if and only if $E$ is a face of $C$.

See also

* Face lattice
* Polyhedral combinatorics
* Discrete geometry

References

Bibliography

*
*
*
*

External links

*
*
* {{mathworld , urlname=Side , title=Side

Elementary geometry
Convex geometry
Polyhedra
Planar surfaces

de:Fläche (Mathematik)