Boolean SAT Solver on:
[Wikipedia]
[Google]
[Amazon]
In
 Like the satisfiability problem for arbitrary formulas, determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete also; this problem is called 3-SAT, 3CNFSAT, or 3-satisfiability.
To reduce the unrestricted SAT problem to 3-SAT, transform each clause to a conjunction of clauses
:
:
:
:
:
where are fresh variables not occurring elsewhere.
Although the two formulas are not
Like the satisfiability problem for arbitrary formulas, determining the satisfiability of a formula in conjunctive normal form where each clause is limited to at most three literals is NP-complete also; this problem is called 3-SAT, 3CNFSAT, or 3-satisfiability.
To reduce the unrestricted SAT problem to 3-SAT, transform each clause to a conjunction of clauses
:
:
:
:
:
where are fresh variables not occurring elsewhere.
Although the two formulas are not
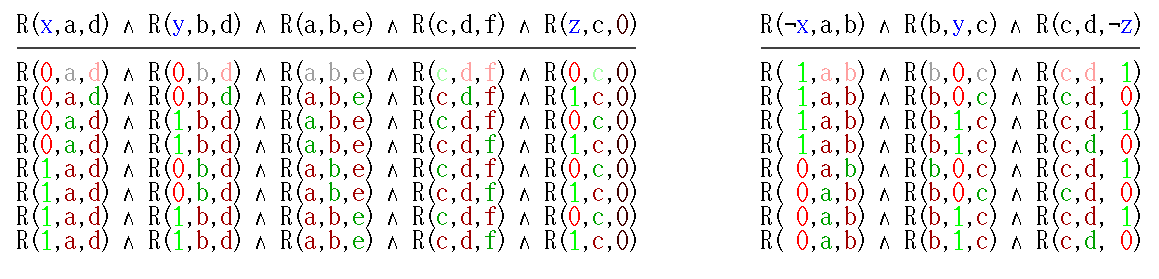 A variant of the 3-satisfiability problem is the one-in-three 3-SAT (also known variously as 1-in-3-SAT and exactly-1 3-SAT).
Given a conjunctive normal form with three literals per clause, the problem is to determine whether there exists a truth assignment to the variables so that each clause has ''exactly'' one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has ''at least'' one TRUE literal.
Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator ''R'' that is TRUE just if exactly one of its arguments is. When all literals of a one-in-three 3-SAT formula are positive, the satisfiability problem is called one-in-three positive 3-SAT.
One-in-three 3-SAT, together with its positive case, is listed as NP-complete problem "LO4" in the standard reference, ''Computers and Intractability: A Guide to the Theory of NP-Completeness''
by Michael R. Garey and David S. Johnson. One-in-three 3-SAT was proved to be NP-complete by
A variant of the 3-satisfiability problem is the one-in-three 3-SAT (also known variously as 1-in-3-SAT and exactly-1 3-SAT).
Given a conjunctive normal form with three literals per clause, the problem is to determine whether there exists a truth assignment to the variables so that each clause has ''exactly'' one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has ''at least'' one TRUE literal.
Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator ''R'' that is TRUE just if exactly one of its arguments is. When all literals of a one-in-three 3-SAT formula are positive, the satisfiability problem is called one-in-three positive 3-SAT.
One-in-three 3-SAT, together with its positive case, is listed as NP-complete problem "LO4" in the standard reference, ''Computers and Intractability: A Guide to the Theory of NP-Completeness''
by Michael R. Garey and David S. Johnson. One-in-three 3-SAT was proved to be NP-complete by
Microprocessor Verification Using Efficient Decision Procedures for a Logic of Equality with Uninterpreted Functions
in Analytic Tableaux and Related Methods, pp. 1–13, 1999. ''etc.'' Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints. The satisfiability problem becomes more difficult if both "for all" (
SAT Game
try solving a Boolean satisfiability problem yourself
The international SAT competition website
International Conference on Theory and Applications of Satisfiability Testing
Journal on Satisfiability, Boolean Modeling and Computation
SAT Live, an aggregate website for research on the satisfiability problem
Yearly evaluation of MaxSAT solvers
SIGDA
b
Prof. Karem Sakallah
Original text is availabl
' {{DEFAULTSORT:Boolean Satisfiability Problem Boolean algebra Electronic design automation Formal methods Logic in computer science NP-complete problems Satisfiability problems
logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premis ...
and computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, the Boolean satisfiability problem (sometimes called propositional satisfiability problem and abbreviated SATISFIABILITY, SAT or B-SAT) is the problem of determining if there exists an interpretation
Interpretation may refer to:
Culture
* Aesthetic interpretation, an explanation of the meaning of a work of art
* Allegorical interpretation, an approach that assumes a text should not be interpreted literally
* Dramatic Interpretation, an event ...
that satisfies a given Boolean
Any kind of logic, function, expression, or theory based on the work of George Boole is considered Boolean.
Related to this, "Boolean" may refer to:
* Boolean data type, a form of data with only two possible values (usually "true" and "false" ...
formula. In other words, it asks whether the variables of a given Boolean formula can be consistently replaced by the values TRUE or FALSE in such a way that the formula evaluates to TRUE. If this is the case, the formula is called ''satisfiable''. On the other hand, if no such assignment exists, the function expressed by the formula is FALSE
False or falsehood may refer to:
* False (logic), the negation of truth in classical logic
*Lie or falsehood, a type of deception in the form of an untruthful statement
* false (Unix), a Unix command
* ''False'' (album), a 1992 album by Gorefest
* ...
for all possible variable assignments and the formula is ''unsatisfiable''. For example, the formula "''a'' AND NOT ''b''" is satisfiable because one can find the values ''a'' = TRUE and ''b'' = FALSE, which make (''a'' AND NOT ''b'') = TRUE. In contrast, "''a'' AND NOT ''a''" is unsatisfiable.
SAT is the first problem that was proved to be NP-complete
In computational complexity theory, a problem is NP-complete when:
# it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by tryin ...
; see Cook–Levin theorem
In computational complexity theory, the Cook–Levin theorem, also known as Cook's theorem, states that the Boolean satisfiability problem is NP-complete. That is, it is in NP, and any problem in NP can be reduced in polynomial time by a determi ...
. This means that all problems in the complexity class NP, which includes a wide range of natural decision and optimization problems, are at most as difficult to solve as SAT. There is no known algorithm that efficiently solves each SAT problem, and it is generally believed that no such algorithm exists; yet this belief has not been proved mathematically, and resolving the question of whether SAT has a polynomial-time
In computer science, the time complexity is the computational complexity that describes the amount of computer time it takes to run an algorithm. Time complexity is commonly estimated by counting the number of elementary operations performed by t ...
algorithm is equivalent to the P versus NP problem
The P versus NP problem is a major unsolved problem in theoretical computer science. In informal terms, it asks whether every problem whose solution can be quickly verified can also be quickly solved.
The informal term ''quickly'', used above ...
, which is a famous open problem in the theory of computing.
Nevertheless, as of 2007, heuristic SAT-algorithms are able to solve problem instances involving tens of thousands of variables and formulas consisting of millions of symbols, which is sufficient for many practical SAT problems from, e.g., artificial intelligence
Artificial intelligence (AI) is intelligence—perceiving, synthesizing, and inferring information—demonstrated by machines, as opposed to intelligence displayed by animals and humans. Example tasks in which this is done include speech r ...
, circuit design
The process of circuit design can cover systems ranging from complex electronic systems down to the individual transistors within an integrated circuit. One person can often do the design process without needing a planned or structured design ...
, and automatic theorem proving
Automated theorem proving (also known as ATP or automated deduction) is a subfield of automated reasoning and mathematical logic dealing with proving mathematical theorems by computer programs. Automated reasoning over mathematical proof was a maj ...
.
Definitions
A ''propositional logic
Propositional calculus is a branch of logic. It is also called propositional logic, statement logic, sentential calculus, sentential logic, or sometimes zeroth-order logic. It deals with propositions (which can be true or false) and relations ...
formula'', also called ''Boolean expression'', is built from variables, operators AND (conjunction
Conjunction may refer to:
* Conjunction (grammar), a part of speech
* Logical conjunction, a mathematical operator
** Conjunction introduction, a rule of inference of propositional logic
* Conjunction (astronomy), in which two astronomical bodies ...
, also denoted by ∧), OR (disjunction
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor ...
, ∨), NOT (negation
In logic, negation, also called the logical complement, is an operation that takes a proposition P to another proposition "not P", written \neg P, \mathord P or \overline. It is interpreted intuitively as being true when P is false, and fals ...
, ¬), and parentheses.
A formula is said to be ''satisfiable'' if it can be made TRUE by assigning appropriate logical value
In logic and mathematics, a truth value, sometimes called a logical value, is a value indicating the relation of a proposition to truth, which in classical logic has only two possible values ('' true'' or ''false'').
Computing
In some prog ...
s (i.e. TRUE, FALSE) to its variables.
The ''Boolean satisfiability problem'' (SAT) is, given a formula, to check whether it is satisfiable.
This decision problem
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding by means of an algorithm whethe ...
is of central importance in many areas of computer science
Computer science is the study of computation, automation, and information. Computer science spans theoretical disciplines (such as algorithms, theory of computation, information theory, and automation) to practical disciplines (includin ...
, including theoretical computer science
Theoretical computer science (TCS) is a subset of general computer science and mathematics that focuses on mathematical aspects of computer science such as the theory of computation, lambda calculus, and type theory.
It is difficult to circumsc ...
, complexity theory, algorithmics
Algorithmics is the systematic study of the design and analysis of algorithms. It is fundamental and one of the oldest fields of computer science. It includes algorithm design, the art of building a procedure which can solve efficiently a specific ...
, cryptography
Cryptography, or cryptology (from grc, , translit=kryptós "hidden, secret"; and ''graphein'', "to write", or ''-logia'', "study", respectively), is the practice and study of techniques for secure communication in the presence of adve ...
and artificial intelligence
Artificial intelligence (AI) is intelligence—perceiving, synthesizing, and inferring information—demonstrated by machines, as opposed to intelligence displayed by animals and humans. Example tasks in which this is done include speech r ...
.
Conjunctive normal form
A ''literal'' is either a variable (in which case it is called a ''positive literal'') or the negation of a variable (called a ''negative literal''). A ''clause'' is a disjunction of literals (or a single literal). A clause is called a ''Horn clause In mathematical logic and logic programming, a Horn clause is a logical formula of a particular rule-like form which gives it useful properties for use in logic programming, formal specification, and model theory. Horn clauses are named for the logi ...
'' if it contains at most one positive literal.
A formula is in ''conjunctive normal form
In Boolean logic, a formula is in conjunctive normal form (CNF) or clausal normal form if it is a conjunction of one or more clauses, where a clause is a disjunction of literals; otherwise put, it is a product of sums or an AND of ORs. As a cano ...
'' (CNF) if it is a conjunction of clauses (or a single clause).
For example, is a positive literal, is a negative literal, is a clause. The formula is in conjunctive normal form; its first and third clauses are Horn clauses, but its second clause is not. The formula is satisfiable, by choosing ''x''1 = FALSE, ''x''2 = FALSE, and ''x''3 arbitrarily, since (FALSE ∨ ¬FALSE) ∧ (¬FALSE ∨ FALSE ∨ ''x''3) ∧ ¬FALSE evaluates to (FALSE ∨ TRUE) ∧ (TRUE ∨ FALSE ∨ ''x''3) ∧ TRUE, and in turn to TRUE ∧ TRUE ∧ TRUE (i.e. to TRUE). In contrast, the CNF formula ''a'' ∧ ¬''a'', consisting of two clauses of one literal, is unsatisfiable, since for ''a''=TRUE or ''a''=FALSE it evaluates to TRUE ∧ ¬TRUE (i.e., FALSE) or FALSE ∧ ¬FALSE (i.e., again FALSE), respectively.
For some versions of the SAT problem, it is useful to define the notion of a ''generalized conjunctive normal form'' formula, viz. as a conjunction of arbitrarily many ''generalized clauses'', the latter being of the form for some Boolean function
In mathematics, a Boolean function is a function whose arguments and result assume values from a two-element set (usually , or ). Alternative names are switching function, used especially in older computer science literature, and truth function ...
''R'' and (ordinary) literals . Different sets of allowed boolean functions lead to different problem versions. As an example, ''R''(¬''x'',''a'',''b'') is a generalized clause, and ''R''(¬''x'',''a'',''b'') ∧ ''R''(''b'',''y'',''c'') ∧ ''R''(''c'',''d'',¬''z'') is a generalized conjunctive normal form. This formula is used below
Below may refer to:
*Earth
* Ground (disambiguation)
* Soil
* Floor
* Bottom (disambiguation)
* Less than
*Temperatures below freezing
* Hell or underworld
People with the surname
* Ernst von Below (1863–1955), German World War I general
* Fr ...
, with ''R'' being the ternary operator that is TRUE just when exactly one of its arguments is.
Using the laws of Boolean algebra
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas ...
, every propositional logic formula can be transformed into an equivalent conjunctive normal form, which may, however, be exponentially longer. For example, transforming the formula
(''x''1∧''y''1) ∨ (''x''2∧''y''2) ∨ ... ∨ (''x''''n''∧''y''''n'')
into conjunctive normal form yields
:
:
:
:
:
:
:
:;
while the former is a disjunction of ''n'' conjunctions of 2 variables, the latter consists of 2''n'' clauses of ''n'' variables.
However, with use of the Tseytin transformation The Tseytin transformation, alternatively written Tseitin transformation, takes as input an arbitrary combinatorial logic circuit and produces a boolean formula in conjunctive normal form (CNF), which can be solved by a CNF-SAT solver. The length ...
, we may find an equisatisfiable conjunctive normal form formula with length linear in the size of the original propositional logic formula.
Complexity
SAT was the first knownNP-complete
In computational complexity theory, a problem is NP-complete when:
# it is a problem for which the correctness of each solution can be verified quickly (namely, in polynomial time) and a brute-force search algorithm can find a solution by tryin ...
problem, as proved by Stephen Cook
Stephen Arthur Cook (born December 14, 1939) is an American-Canadian computer scientist and mathematician who has made significant contributions to the fields of complexity theory and proof complexity. He is a university professor at the Univ ...
at the University of Toronto
The University of Toronto (UToronto or U of T) is a public research university in Toronto, Ontario, Canada, located on the grounds that surround Queen's Park. It was founded by royal charter in 1827 as King's College, the first institu ...
in 1971 and independently by Leonid Levin
Leonid Anatolievich Levin ( ; russian: Леони́д Анато́льевич Ле́вин; uk, Леоні́д Анато́лійович Ле́він; born November 2, 1948) is a Soviet-American mathematician and computer scientist.
He is kn ...
at the Russian Academy of Sciences
The Russian Academy of Sciences (RAS; russian: Росси́йская акаде́мия нау́к (РАН) ''Rossíyskaya akadémiya naúk'') consists of the national academy of Russia; a network of scientific research institutes from across t ...
in 1973. Until that time, the concept of an NP-complete problem did not even exist.
The proof shows how every decision problem in the complexity class
In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and memory.
In general, a complexity class is defined in terms ...
NP can be reduced to the SAT problem for CNFThe SAT problem for ''arbitrary'' formulas is NP-complete, too, since it is easily shown to be in NP, and it cannot be easier than SAT for CNF formulas. formulas, sometimes called CNFSAT.
A useful property of Cook's reduction is that it preserves the number of accepting answers. For example, deciding whether a given graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
has a 3-coloring is another problem in NP; if a graph has 17 valid 3-colorings, the SAT formula produced by the Cook–Levin reduction will have 17 satisfying assignments.
NP-completeness only refers to the run-time of the worst case instances. Many of the instances that occur in practical applications can be solved much more quickly. See Algorithms for solving SAT below.
3-satisfiability
logically equivalent
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises ...
, they are equisatisfiable
In Mathematical logic (a subtopic within the field of formal logic), two formulae are equisatisfiable if the first formula is satisfiable whenever the second is and vice versa; in other words, either both formulae are satisfiable or both are not. E ...
. The formula resulting from transforming all clauses is at most 3 times as long as its original, i.e. the length growth is polynomial.
3-SAT is one of Karp's 21 NP-complete problems
In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete. In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the bo ...
, and it is used as a starting point for proving that other problems are also NP-hard
In computational complexity theory, NP-hardness ( non-deterministic polynomial-time hardness) is the defining property of a class of problems that are informally "at least as hard as the hardest problems in NP". A simple example of an NP-hard pr ...
.i.e. at least as hard as every other problem in NP. A decision problem is NP-complete if and only if it is in NP and is NP-hard. This is done by polynomial-time reduction
In computational complexity theory, a polynomial-time reduction is a method for solving one problem using another. One shows that if a hypothetical subroutine solving the second problem exists, then the first problem can be solved by transforming ...
from 3-SAT to the other problem. An example of a problem where this method has been used is the clique problem
In computer science, the clique problem is the computational problem of finding cliques (subsets of vertices, all adjacent to each other, also called complete subgraphs) in a graph. It has several different formulations depending on which cliq ...
: given a CNF formula consisting of ''c'' clauses, the corresponding graph
Graph may refer to:
Mathematics
*Graph (discrete mathematics), a structure made of vertices and edges
**Graph theory, the study of such graphs and their properties
*Graph (topology), a topological space resembling a graph in the sense of discre ...
consists of a vertex for each literal, and an edge between each two non-contradictingi.e. such that one literal is not the negation of the other literals from different clauses, cf. picture. The graph has a ''c''-clique if and only if the formula is satisfiable.
There is a simple randomized algorithm due to Schöning (1999) that runs in time (4/3)''n'' where ''n'' is the number of variables in the 3-SAT proposition, and succeeds with high probability to correctly decide 3-SAT.
The exponential time hypothesis
In computational complexity theory, the exponential time hypothesis is an unproven computational hardness assumption that was formulated by . It states that satisfiability of 3-CNF Boolean formulas cannot be solved more quickly than exponential ...
asserts that no algorithm can solve 3-SAT (or indeed ''k''-SAT for any ) in time (i.e., fundamentally faster than exponential in ''n'').
Selman, Mitchell, and Levesque (1996) give empirical data on the difficulty of randomly generated 3-SAT formulas, depending on their size parameters.
Difficulty is measured in number recursive calls made by a DPLL algorithm
In logic and computer science, the Davis–Putnam–Logemann–Loveland (DPLL) algorithm is a complete, backtracking-based search algorithm for deciding the satisfiability of propositional logic formulae in conjunctive normal form, i.e. for solvi ...
.
3-satisfiability can be generalized to k-satisfiability (k-SAT, also k-CNF-SAT), when formulas in CNF are considered with each clause containing up to ''k'' literals.
However, since for any ''k'' ≥ 3, this problem can neither be easier than 3-SAT nor harder than SAT, and the latter two are NP-complete, so must be k-SAT.
Some authors restrict k-SAT to CNF formulas with exactly k literals. This doesn't lead to a different complexity class either, as each clause with ''j'' < ''k'' literals can be padded with fixed dummy variables to
.
After padding all clauses, 2''k''-1 extra clausesviz. all maxterms
In Boolean algebra, any Boolean function can be expressed in the canonical disjunctive normal form ( CDNF) or minterm canonical form and its dual canonical conjunctive normal form (CCNF) or maxterm canonical form. Other canonical forms include ...
that can be built with , except have to be appended to ensure that only can lead to a satisfying assignment. Since ''k'' doesn't depend on the formula length, the extra clauses lead to a constant increase in length. For the same reason, it does not matter whether duplicate literals are allowed in clauses, as in .
Special cases of SAT
Conjunctive normal form
Conjunctive normal form (in particular with 3 literals per clause) is often considered the canonical representation for SAT formulas. As shown above, the general SAT problem reduces to 3-SAT, the problem of determining satisfiability for formulas in this form.Disjunctive normal form
SAT is trivial if the formulas are restricted to those indisjunctive normal form
In boolean logic, a disjunctive normal form (DNF) is a canonical normal form of a logical formula consisting of a disjunction of conjunctions; it can also be described as an OR of ANDs, a sum of products, or (in philosophical logic) a ''cluster co ...
, that is, they are a disjunction of conjunctions of literals. Such a formula is indeed satisfiable if and only if at least one of its conjunctions is satisfiable, and a conjunction is satisfiable if and only if it does not contain both ''x'' and NOT ''x'' for some variable ''x''. This can be checked in linear time. Furthermore, if they are restricted to being in full disjunctive normal form, in which every variable appears exactly once in every conjunction, they can be checked in constant time (each conjunction represents one satisfying assignment). But it can take exponential time and space to convert a general SAT problem to disjunctive normal form; for an example exchange "∧" and "∨" in the above exponential blow-up example for conjunctive normal forms.
Exactly-1 3-satisfiability
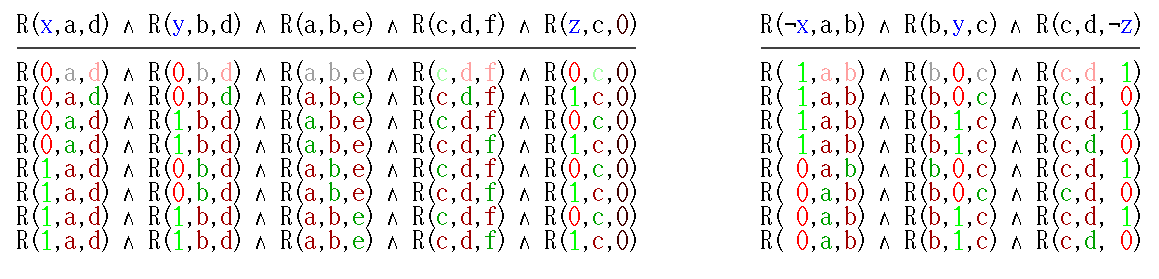 A variant of the 3-satisfiability problem is the one-in-three 3-SAT (also known variously as 1-in-3-SAT and exactly-1 3-SAT).
Given a conjunctive normal form with three literals per clause, the problem is to determine whether there exists a truth assignment to the variables so that each clause has ''exactly'' one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has ''at least'' one TRUE literal.
Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator ''R'' that is TRUE just if exactly one of its arguments is. When all literals of a one-in-three 3-SAT formula are positive, the satisfiability problem is called one-in-three positive 3-SAT.
One-in-three 3-SAT, together with its positive case, is listed as NP-complete problem "LO4" in the standard reference, ''Computers and Intractability: A Guide to the Theory of NP-Completeness''
by Michael R. Garey and David S. Johnson. One-in-three 3-SAT was proved to be NP-complete by
A variant of the 3-satisfiability problem is the one-in-three 3-SAT (also known variously as 1-in-3-SAT and exactly-1 3-SAT).
Given a conjunctive normal form with three literals per clause, the problem is to determine whether there exists a truth assignment to the variables so that each clause has ''exactly'' one TRUE literal (and thus exactly two FALSE literals). In contrast, ordinary 3-SAT requires that every clause has ''at least'' one TRUE literal.
Formally, a one-in-three 3-SAT problem is given as a generalized conjunctive normal form with all generalized clauses using a ternary operator ''R'' that is TRUE just if exactly one of its arguments is. When all literals of a one-in-three 3-SAT formula are positive, the satisfiability problem is called one-in-three positive 3-SAT.
One-in-three 3-SAT, together with its positive case, is listed as NP-complete problem "LO4" in the standard reference, ''Computers and Intractability: A Guide to the Theory of NP-Completeness''
by Michael R. Garey and David S. Johnson. One-in-three 3-SAT was proved to be NP-complete by Thomas Jerome Schaefer
Thomas Jerome Schaefer is an American mathematician.
He obtained his Ph.D. in December 1978 from the University of California, Berkeley, where he worked in the Department of Mathematics. His Ph.D. advisor was Richard M. Karp.
He is well-known f ...
as a special case of Schaefer's dichotomy theorem
In computational complexity theory, a branch of computer science, Schaefer's dichotomy theorem states necessary and sufficient conditions under which a finite set ''S'' of relations over the Boolean domain yields polynomial-time or NP-complete pro ...
, which asserts that any problem generalizing Boolean satisfiability in a certain way is either in the class P or is NP-complete.
Schaefer gives a construction allowing an easy polynomial-time reduction from 3-SAT to one-in-three 3-SAT. Let "(''x'' or ''y'' or ''z'')" be a clause in a 3CNF formula. Add six fresh boolean variables ''a'', ''b'', ''c'', ''d'', ''e'', and ''f'', to be used to simulate this clause and no other.
Then the formula ''R''(''x'',''a'',''d'') ∧ ''R''(''y'',''b'',''d'') ∧ ''R''(''a'',''b'',''e'') ∧ ''R''(''c'',''d'',''f'') ∧ ''R''(''z'',''c'',FALSE) is satisfiable by some setting of the fresh variables if and only if at least one of ''x'', ''y'', or ''z'' is TRUE, see picture (left). Thus any 3-SAT instance with ''m'' clauses and ''n'' variables may be converted into an equisatisfiable
In Mathematical logic (a subtopic within the field of formal logic), two formulae are equisatisfiable if the first formula is satisfiable whenever the second is and vice versa; in other words, either both formulae are satisfiable or both are not. E ...
one-in-three 3-SAT instance with 5''m'' clauses and ''n''+6''m'' variables.
Another reduction involves only four fresh variables and three clauses: ''R''(¬''x'',''a'',''b'') ∧ ''R''(''b'',''y'',''c'') ∧ R(''c'',''d'',¬''z''), see picture (right).
Not-all-equal 3-satisfiability
Another variant is the not-all-equal 3-satisfiability problem (also called NAE3SAT). Given a conjunctive normal form with three literals per clause, the problem is to determine if an assignment to the variables exists such that in no clause all three literals have the same truth value. This problem is NP-complete, too, even if no negation symbols are admitted, by Schaefer's dichotomy theorem.Linear SAT
A 3-SAT formula is ''Linear SAT'' (''LSAT'') if each clause (viewed as a set of literals) intersects at most one other clause, and, moreover, if two clauses intersect, then they have exactly one literal in common. An LSAT formula can be depicted as a set of disjoint semi-closed intervals on a line. Deciding whether an LSAT formula is satisfiable is NP-complete.2-satisfiability
SAT is easier if the number of literals in a clause is limited to at most 2, in which case the problem is called2-SAT
In computer science, 2-satisfiability, 2-SAT or just 2SAT is a computational problem of assigning values to variables, each of which has two possible values, in order to satisfy a system of constraints on pairs of variables. It is a special case ...
. This problem can be solved in polynomial time, and in fact is complete
Complete may refer to:
Logic
* Completeness (logic)
* Completeness of a theory, the property of a theory that every formula in the theory's language or its negation is provable
Mathematics
* The completeness of the real numbers, which implies ...
for the complexity class NL. If additionally all OR operations in literals are changed to XOR
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , , ...
operations, the result is called exclusive-or 2-satisfiability, which is a problem complete for the complexity class SL = L.
Horn-satisfiability
The problem of deciding the satisfiability of a given conjunction ofHorn clause In mathematical logic and logic programming, a Horn clause is a logical formula of a particular rule-like form which gives it useful properties for use in logic programming, formal specification, and model theory. Horn clauses are named for the logi ...
s is called Horn-satisfiability, or HORN-SAT.
It can be solved in polynomial time by a single step of the Unit propagation
Unit propagation (UP) or Boolean Constraint propagation (BCP) or the one-literal rule (OLR) is a procedure of automated theorem proving that can simplify a set of (usually propositional) clauses.
Definition
The procedure is based on unit clauses ...
algorithm, which produces the single minimal model of the set of Horn clauses (w.r.t. the set of literals assigned to TRUE).
Horn-satisfiability is P-complete In computational complexity theory, a decision problem is P-complete (complete for the complexity class P) if it is in P and every problem in P can be reduced to it by an appropriate reduction.
The notion of P-complete decision problems is usef ...
. It can be seen as P's version of the Boolean satisfiability problem.
Also, deciding the truth of quantified Horn formulas can be done in polynomial time.
Horn clauses are of interest because they are able to express implication of one variable from a set of other variables. Indeed, one such clause ¬''x''1 ∨ ... ∨ ¬''x''''n'' ∨ ''y'' can be rewritten as ''x''1 ∧ ... ∧ ''x''''n'' → ''y'', that is, if ''x''1,...,''x''''n'' are all TRUE, then ''y'' needs to be TRUE as well.
A generalization of the class of Horn formulae is that of renameable-Horn formulae, which is the set of formulae that can be placed in Horn form by replacing some variables with their respective negation.
For example, (''x''1 ∨ ¬''x''2) ∧ (¬''x''1 ∨ ''x''2 ∨ ''x''3) ∧ ¬''x''1 is not a Horn formula, but can be renamed to the Horn formula (''x''1 ∨ ¬''x''2) ∧ (¬''x''1 ∨ ''x''2 ∨ ¬''y''3) ∧ ¬''x''1 by introducing ''y''3 as negation of ''x''3.
In contrast, no renaming of (''x''1 ∨ ¬''x''2 ∨ ¬''x''3) ∧ (¬''x''1 ∨ ''x''2 ∨ ''x''3) ∧ ¬''x''1 leads to a Horn formula.
Checking the existence of such a replacement can be done in linear time; therefore, the satisfiability of such formulae is in P as it can be solved by first performing this replacement and then checking the satisfiability of the resulting Horn formula.
XOR-satisfiability
Another special case is the class of problems where each clause contains XOR (i.e.exclusive or
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , ...
) rather than (plain) OR operators.Formally, generalized conjunctive normal forms with a ternary boolean function ''R'' are employed, which is TRUE just if 1 or 3 of its arguments is. An input clause with more than 3 literals can be transformed into an equisatisfiable conjunction of clauses á 3 literals similar to above; i.e. XOR-SAT can be reduced to XOR-3-SAT.
This is in P, since an XOR-SAT formula can also be viewed as a system of linear equations mod 2, and can be solved in cubic time by Gaussian elimination
In mathematics, Gaussian elimination, also known as row reduction, is an algorithm for solving systems of linear equations. It consists of a sequence of operations performed on the corresponding matrix of coefficients. This method can also be used ...
; see the box for an example. This recast is based on the kinship between Boolean algebras and Boolean rings, and the fact that arithmetic modulo two forms a finite field
In mathematics, a finite field or Galois field (so-named in honor of Évariste Galois) is a field that contains a finite number of elements. As with any field, a finite field is a set on which the operations of multiplication, addition, subt ...
. Since ''a'' XOR ''b'' XOR ''c'' evaluates to TRUE if and only if exactly 1 or 3 members of are TRUE, each solution of the 1-in-3-SAT problem for a given CNF formula is also a solution of the XOR-3-SAT problem, and in turn each solution of XOR-3-SAT is a solution of 3-SAT, cf. picture. As a consequence, for each CNF formula, it is possible to solve the XOR-3-SAT problem defined by the formula, and based on the result infer either that the 3-SAT problem is solvable or that the 1-in-3-SAT problem is unsolvable.
Provided that the complexity classes P and NP are not equal, neither 2-, nor Horn-, nor XOR-satisfiability is NP-complete, unlike SAT.
Schaefer's dichotomy theorem
The restrictions above (CNF, 2CNF, 3CNF, Horn, XOR-SAT) bound the considered formulae to be conjunctions of subformulae; each restriction states a specific form for all subformulae: for example, only binary clauses can be subformulae in 2CNF. Schaefer's dichotomy theorem states that, for any restriction to Boolean functions that can be used to form these subformulae, the corresponding satisfiability problem is in P or NP-complete. The membership in P of the satisfiability of 2CNF, Horn, and XOR-SAT formulae are special cases of this theorem. The following table summarizes some common variants of SAT.Extensions of SAT
An extension that has gained significant popularity since 2003 issatisfiability modulo theories
In computer science and mathematical logic, satisfiability modulo theories (SMT) is the problem of determining whether a mathematical formula is satisfiable. It generalizes the Boolean satisfiability problem (SAT) to more complex formulas involvin ...
(SMT) that can enrich CNF formulas with linear constraints, arrays, all-different constraints, uninterpreted function In mathematical logic, an uninterpreted function or function symbol is one that has no other property than its name and '' n-ary'' form. Function symbols are used, together with constants and variables, to form terms.
The theory of uninterpreted ...
s,R. E. Bryant, S. M. German, and M. N. VelevMicroprocessor Verification Using Efficient Decision Procedures for a Logic of Equality with Uninterpreted Functions
in Analytic Tableaux and Related Methods, pp. 1–13, 1999. ''etc.'' Such extensions typically remain NP-complete, but very efficient solvers are now available that can handle many such kinds of constraints. The satisfiability problem becomes more difficult if both "for all" (
∀
A mathematical symbol is a figure or a combination of figures that is used to represent a mathematical object, an action on mathematical objects, a relation between mathematical objects, or for structuring the other symbols that occur in a formula ...
) and "there exists" (∃
In predicate logic, an existential quantification is a type of quantifier, a logical constant which is interpreted as "there exists", "there is at least one", or "for some". It is usually denoted by the logical operator symbol ∃, which, whe ...
) quantifiers are allowed to bind the Boolean variables.
An example of such an expression would be ; it is valid, since for all values of ''x'' and ''y'', an appropriate value of ''z'' can be found, viz. ''z''=TRUE if both ''x'' and ''y'' are FALSE, and ''z''=FALSE else.
SAT itself (tacitly) uses only ∃ quantifiers.
If only ∀ quantifiers are allowed instead, the so-called tautology problem is obtained, which is co-NP-complete
In complexity theory, computational problems that are co-NP-complete are those that are the hardest problems in co-NP, in the sense that any problem in co-NP can be reformulated as a special case of any co-NP-complete problem with only polynomial ...
.
If both quantifiers are allowed, the problem is called the quantified Boolean formula problem In computational complexity theory, the language TQBF is a formal language consisting of the true quantified Boolean formulas. A (fully) quantified Boolean formula is a formula in quantified propositional logic where every variable is quantified ( ...
(QBF), which can be shown to be PSPACE-complete In computational complexity theory, a decision problem is PSPACE-complete if it can be solved using an amount of memory that is polynomial in the input length ( polynomial space) and if every other problem that can be solved in polynomial space can ...
. It is widely believed that PSPACE-complete problems are strictly harder than any problem in NP, although this has not yet been proved. Using highly parallel ''P system : ''For the computer p-System, see UCSD p-System.''
A P system is a computational model in the field of computer science that performs calculations using a biologically inspired process. They are based upon the structure of biological cells, abstra ...
s'', QBF-SAT problems can be solved in linear time.
Ordinary SAT asks if there is at least one variable assignment that makes the formula true. A variety of variants deal with the number of such assignments:
* MAJ-SAT asks if the majority of all assignments make the formula TRUE. It is known to be complete for PP, a probabilistic class.
* #SAT, the problem of counting how many variable assignments satisfy a formula, is a counting problem, not a decision problem, and is #P-complete.
* UNIQUE SAT is the problem of determining whether a formula has exactly one assignment. It is complete for US, the complexity class
In computational complexity theory, a complexity class is a set of computational problems of related resource-based complexity. The two most commonly analyzed resources are time and memory.
In general, a complexity class is defined in terms ...
describing problems solvable by a non-deterministic polynomial time Turing machine
A Turing machine is a mathematical model of computation describing an abstract machine that manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, it is capable of implementing any computer algor ...
that accepts when there is exactly one nondeterministic accepting path and rejects otherwise.
*UNAMBIGUOUS-SAT is the name given to the satisfiability problem when the input is restricted to formulas having at most one satisfying assignment. The problem is also called USAT. A solving algorithm for UNAMBIGUOUS-SAT is allowed to exhibit any behavior, including endless looping, on a formula having several satisfying assignments. Although this problem seems easier, Valiant and Vazirani have shown that if there is a practical (i.e. randomized polynomial-time) algorithm to solve it, then all problems in NP can be solved just as easily.
* MAX-SAT, the maximum satisfiability problem In computational complexity theory, the maximum satisfiability problem (MAX-SAT) is the problem of determining the maximum number of clauses, of a given Boolean formula in conjunctive normal form, that can be made true by an assignment of truth val ...
, is an FNP generalization of SAT. It asks for the maximum number of clauses which can be satisfied by any assignment. It has efficient approximation algorithm
In computer science and operations research, approximation algorithms are efficient algorithms that find approximate solutions to optimization problems (in particular NP-hard problems) with provable guarantees on the distance of the returned solu ...
s, but is NP-hard to solve exactly. Worse still, it is APX
In computational complexity theory, the class APX (an abbreviation of "approximable") is the set of NP optimization problems that allow polynomial-time approximation algorithms with approximation ratio bounded by a constant (or constant-facto ...
-complete, meaning there is no polynomial-time approximation scheme
In computer science (particularly algorithmics), a polynomial-time approximation scheme (PTAS) is a type of approximation algorithm for optimization problems (most often, NP-hard optimization problems).
A PTAS is an algorithm which takes an in ...
(PTAS) for this problem unless P=NP.
*WMSAT is the problem of finding an assignment of minimum weight that satisfy a monotone Boolean formula (i.e. a formula without any negation). Weights of propositional variables are given in the input of the problem. The weight of an assignment is the sum of weights of true variables. That problem is NP-complete (see Th. 1 of ).
Other generalizations include satisfiability for first
First or 1st is the ordinal form of the number one (#1).
First or 1st may also refer to:
*World record, specifically the first instance of a particular achievement
Arts and media Music
* 1$T, American rapper, singer-songwriter, DJ, and reco ...
- and second-order logic
In logic and mathematics, second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory.
First-order logic quantifies ...
, constraint satisfaction problem
Constraint satisfaction problems (CSPs) are mathematical questions defined as a set of objects whose state must satisfy a number of constraints or limitations. CSPs represent the entities in a problem as a homogeneous collection of finite constr ...
s, 0-1 integer programming
Linear programming (LP), also called linear optimization, is a method to achieve the best outcome (such as maximum profit or lowest cost) in a mathematical model whose requirements are represented by linear relationships. Linear programming is ...
.
Finding a satisfying assignment
While SAT is adecision problem
In computability theory and computational complexity theory, a decision problem is a computational problem that can be posed as a yes–no question of the input values. An example of a decision problem is deciding by means of an algorithm whethe ...
, the search problem
In computational complexity theory and computability theory, a search problem is a type of computational problem represented by a binary relation. If ''R'' is a binary relation such that field(''R'') ⊆ Γ+ and ''T'' is a Turing machine, then '' ...
of finding a satisfying assignment reduces to SAT. That is, each algorithm which correctly answers if an instance of SAT is solvable can be used to find a satisfying assignment. First, the question is asked on the given formula Φ. If the answer is "no", the formula is unsatisfiable. Otherwise, the question is asked on the partly instantiated formula Φ , i.e. Φ with the first variable ''x''1 replaced by TRUE, and simplified accordingly. If the answer is "yes", then ''x''1=TRUE, otherwise ''x''1=FALSE. Values of other variables can be found subsequently in the same way. In total, ''n''+1 runs of the algorithm are required, where ''n'' is the number of distinct variables in Φ.
This property is used in several theorems in complexity theory:
: NP ⊆ P/poly
In computational complexity theory, P/poly is a complexity class representing problems that can be solved by small circuits. More precisely, it is the set of formal languages that have polynomial-size circuit families. It can also be defined equiva ...
⇒ PH = Σ2 (Karp–Lipton theorem
In complexity theory, the Karp–Lipton theorem states that if the Boolean satisfiability problem (SAT) can be solved by Boolean circuits with a polynomial number of logic gates, then
:\Pi_2 = \Sigma_2 \, and therefore \mathrm = \Sigma_2. \,
...
)
: NP ⊆ BPP ⇒ NP = RP
: P = NP ⇒ FP = FNP
Algorithms for solving SAT
Since the SAT problem is NP-complete, only algorithms with exponential worst-case complexity are known for it. In spite of this, efficient and scalable algorithms for SAT were developed during the 2000s and have contributed to dramatic advances in our ability to automatically solve problem instances involving tens of thousands of variables and millions of constraints (i.e. clauses).. Examples of such problems inelectronic design automation
Electronic design automation (EDA), also referred to as electronic computer-aided design (ECAD), is a category of software tools for designing electronic systems such as integrated circuits and printed circuit boards. The tools work together ...
(EDA) include formal equivalence checking
Formal equivalence checking process is a part of electronic design automation (EDA), commonly used during the development of digital integrated circuits, to formally prove that two representations of a circuit design exhibit exactly the same beha ...
, model checking
In computer science, model checking or property checking is a method for checking whether a finite-state model of a system meets a given specification (also known as correctness). This is typically associated with hardware or software system ...
, formal verification
In the context of hardware and software systems, formal verification is the act of proving or disproving the correctness of intended algorithms underlying a system with respect to a certain formal specification or property, using formal met ...
of microprocessor, pipelined microprocessors, automatic test pattern generation, routing (electronic design automation), routing of FPGAs, Automated planning and scheduling, planning, and Scheduling algorithm, scheduling problems, and so on. A SAT-solving engine is also considered to be an essential component in the electronic design automation
Electronic design automation (EDA), also referred to as electronic computer-aided design (ECAD), is a category of software tools for designing electronic systems such as integrated circuits and printed circuit boards. The tools work together ...
toolbox.
Major techniques used by modern SAT solvers include the Davis–Putnam–Logemann–Loveland algorithm (or DPLL), conflict-driven clause learning (CDCL), and stochastic Local search (constraint satisfaction), local search algorithms such as WalkSAT. Almost all SAT solvers include time-outs, so they will terminate in reasonable time even if they cannot find a solution.
Different SAT solvers will find different instances easy or hard, and some excel at proving unsatisfiability, and others at finding solutions. Recent attempts have been made to learn an instance's satisfiability using deep learning techniques.
SAT solvers are developed and compared in SAT-solving contests. Modern SAT solvers are also having significant impact on the fields of software verification, constraint solving in artificial intelligence, and operations research, among others.
See also
*Unsatisfiable core *Satisfiability modulo theories *Sharp-SAT, Counting SAT *Planar SAT *Karloff–Zwick algorithm *Circuit satisfiabilityNotes
External links
SAT Game
try solving a Boolean satisfiability problem yourself
The international SAT competition website
International Conference on Theory and Applications of Satisfiability Testing
Journal on Satisfiability, Boolean Modeling and Computation
SAT Live, an aggregate website for research on the satisfiability problem
Yearly evaluation of MaxSAT solvers
References
Further reading
(by date of publication) * * * * * * * * ---- ''This article includes material from a column in the ACSIGDA
b
Prof. Karem Sakallah
Original text is availabl
' {{DEFAULTSORT:Boolean Satisfiability Problem Boolean algebra Electronic design automation Formal methods Logic in computer science NP-complete problems Satisfiability problems