Binary Value on:
[Wikipedia]
[Google]
[Amazon]
A binary number is a
 The scribes of ancient Egypt used two different systems for their fractions,
The scribes of ancient Egypt used two different systems for their fractions,
 The ''
The ''
/ref> They were known as ''laghu'' (light) and ''guru'' (heavy) syllables. Pingala's Hindu classic titled
 Leibniz studied binary numbering in 1679; his work appears in his article ''Explication de l'Arithmétique Binaire'' (published in 1703).
The full title of Leibniz's article is translated into English as the ''"Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of
Leibniz studied binary numbering in 1679; his work appears in his article ''Explication de l'Arithmétique Binaire'' (published in 1703).
The full title of Leibniz's article is translated into English as the ''"Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of
/ref> Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows: : 0 0 0 1 numerical value 20 : 0 0 1 0 numerical value 21 : 0 1 0 0 numerical value 22 : 1 0 0 0 numerical value 23 Leibniz interpreted the hexagrams of the ''I Ching'' as evidence of binary calculus. As a
 In 1854, British mathematician
In 1854, British mathematician
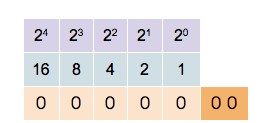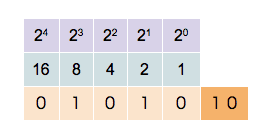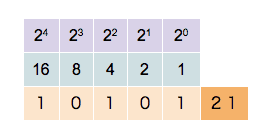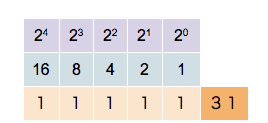
 Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant digit, or ''bit'' (the rightmost one, also called the ''first bit''), except that only the two symbols ''0'' and ''1'' are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:
:0000,
:0001, (rightmost bit starts over, and next digit is incremented)
:0010, 0011, (rightmost two bits start over, and next bit is incremented)
:0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)
:1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 20, the next representing 21, then 22, and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" bit. For example, the binary number 100101 is converted to decimal form as follows:
:1001012 = ( 1 ) × 25 + ( 0 ) × 24 + ( 0 ) × 23 + ( 1 ) × 22 + ( 0 ) × 21 + ( 1 ) × 20
:1001012 = 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
:1001012 = 3710
Binary counting follows the exact same procedure, and again the incremental substitution begins with the least significant digit, or ''bit'' (the rightmost one, also called the ''first bit''), except that only the two symbols ''0'' and ''1'' are available. Thus, after a bit reaches 1 in binary, an increment resets it to 0 but also causes an increment of the next bit to the left:
:0000,
:0001, (rightmost bit starts over, and next digit is incremented)
:0010, 0011, (rightmost two bits start over, and next bit is incremented)
:0100, 0101, 0110, 0111, (rightmost three bits start over, and the next bit is incremented)
:1000, 1001, 1010, 1011, 1100, 1101, 1110, 1111 ...
In the binary system, each bit represents an increasing power of 2, with the rightmost bit representing 20, the next representing 21, then 22, and so on. The value of a binary number is the sum of the powers of 2 represented by each "1" bit. For example, the binary number 100101 is converted to decimal form as follows:
:1001012 = ( 1 ) × 25 + ( 0 ) × 24 + ( 0 ) × 23 + ( 1 ) × 22 + ( 0 ) × 21 + ( 1 ) × 20
:1001012 = 1 × 32 + 0 × 16 + 0 × 8 + 1 × 4 + 0 × 2 + 1 × 1
:1001012 = 3710
1 1 1 0 1 1 1 1 1 0 cross out the "string",
+ 1 0 1 0 1 1 0 0 1 1 + 1 0 1 0 1 1 0 0 1 1 and cross out the digit that was added to it
——————————————————————— ——————————————————————
= 1 1 0 0 1 1 1 0 0 0 1 1 1 0 0 1 1 1 0 0 0 1
The top row shows the carry bits used. Instead of the standard carry from one column to the next, the lowest-ordered "1" with a "1" in the corresponding place value beneath it may be added and a "1" may be carried to one digit past the end of the series. The "used" numbers must be crossed off, since they are already added. Other long strings may likewise be cancelled using the same technique. Then, simply add together any remaining digits normally. Proceeding in this manner gives the final answer of 1 1 0 0 1 1 1 0 0 0 12 (164910). In our simple example using small numbers, the traditional carry method required eight carry operations, yet the long carry method required only two, representing a substantial reduction of effort.
 To convert from a base-10
To convert from a base-10
Binary System
at cut-the-knot
Conversion of Fractions
at cut-the-knot
Sir Francis Bacon's BiLiteral Cypher system
predates binary number system. {{Authority control Binary arithmetic Computer arithmetic Elementary arithmetic Gottfried Wilhelm Leibniz Power-of-two numeral systems
number
A number is a mathematical object used to count, measure, and label. The original examples are the natural numbers 1, 2, 3, 4, and so forth. Numbers can be represented in language with number words. More universally, individual numbers ...
expressed in the base-2 numeral system
A numeral system (or system of numeration) is a writing system for expressing numbers; that is, a mathematical notation for representing numbers of a given set, using digits or other symbols in a consistent manner.
The same sequence of symb ...
or binary numeral system, a method of mathematical expression which uses only two symbols: typically "0" (zero
0 (zero) is a number representing an empty quantity. In place-value notation such as the Hindu–Arabic numeral system, 0 also serves as a placeholder numerical digit, which works by multiplying digits to the left of 0 by the radix, usu ...
) and "1" (one
1 (one, unit, unity) is a number representing a single or the only entity. 1 is also a numerical digit and represents a single unit of counting or measurement. For example, a line segment of ''unit length'' is a line segment of length 1. ...
).
The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented a ...
, or binary digit. Because of its straightforward implementation in digital electronic circuit
Digital electronics is a field of electronics involving the study of digital signals and the engineering of devices that use or produce them. This is in contrast to analog electronics and analog signals.
Digital electronic circuits are usually ...
ry using logic gate
A logic gate is an idealized or physical device implementing a Boolean function, a logical operation performed on one or more binary inputs that produces a single binary output. Depending on the context, the term may refer to an ideal logic ga ...
s, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation.
History
The modern binary number system was studied in Europe in the 16th and 17th centuries byThomas Harriot
Thomas Harriot (; – 2 July 1621), also spelled Harriott, Hariot or Heriot, was an English astronomer, mathematician, ethnographer and translator to whom the theory of refraction is attributed. Thomas Harriot was also recognized for his co ...
, Juan Caramuel y Lobkowitz
Juan Caramuel y Lobkowitz (Juan Caramuel de Lobkowitz, 23 May 1606 in Madrid — 7 or 8 September 1682 in Vigevano) was a Spanish Catholic scholastic philosopher, ecclesiastic, mathematician and writer. He is believed to be a great-grandson of J ...
, and Gottfried Leibniz
Gottfried Wilhelm (von) Leibniz . ( – 14 November 1716) was a German polymath active as a mathematician, philosopher, scientist and diplomat. He is one of the most prominent figures in both the history of philosophy and the history of mat ...
. However, systems related to binary numbers have appeared earlier in multiple cultures including ancient Egypt, China, and India. Leibniz was specifically inspired by the Chinese ''I Ching
The ''I Ching'' or ''Yi Jing'' (, ), usually translated ''Book of Changes'' or ''Classic of Changes'', is an ancient Chinese divination text that is among the oldest of the Chinese classics. Originally a divination manual in the Western Zh ...
''.
Egypt
Egyptian fraction
An Egyptian fraction is a finite sum of distinct unit fractions, such as
\frac+\frac+\frac.
That is, each fraction in the expression has a numerator equal to 1 and a denominator that is a positive integer, and all the denominators differ from eac ...
s (not related to the binary number system) and Horus-Eye fractions (so called because many historians of mathematics believe that the symbols used for this system could be arranged to form the eye of Horus
Horus or Heru, Hor, Har in Ancient Egyptian, is one of the most significant ancient Egyptian deities who served many functions, most notably as god of kingship and the sky. He was worshipped from at least the late prehistoric Egypt until the P ...
, although this has been disputed). Horus-Eye fractions are a binary numbering system for fractional quantities of grain, liquids, or other measures, in which a fraction of a hekat
The hekat or heqat (transcribed ''HqA.t'') was an ancient Egyptian volume unit used to measure grain, bread, and beer.
It equals 4.8 litres, or about 1.056 imperial gallons, in today's measurements. retrieved March 22, 2020 at about 7:00 ...
is expressed as a sum of the binary fractions 1/2, 1/4, 1/8, 1/16, 1/32, and 1/64. Early forms of this system can be found in documents from the Fifth Dynasty of Egypt
The Fifth Dynasty of ancient Egypt (notated Dynasty V) is often combined with Dynasties III, IV and VI under the group title the Old Kingdom. The Fifth Dynasty pharaohs reigned for approximately 150 years, from the early 25th century BC until ...
, approximately 2400 BC, and its fully developed hieroglyphic form dates to the Nineteenth Dynasty of Egypt
The Nineteenth Dynasty of Egypt (notated Dynasty XIX), also known as the Ramessid dynasty, is classified as the second Dynasty of the Ancient Egyptian New Kingdom period, lasting from 1292 BC to 1189 BC. The 19th Dynasty and the 20th Dynasty furt ...
, approximately 1200 BC.
The method used for ancient Egyptian multiplication
In mathematics, ancient Egyptian multiplication (also known as Egyptian multiplication, Ethiopian multiplication, Russian multiplication, or peasant multiplication), one of two multiplication methods used by scribes, is a systematic method for mu ...
is also closely related to binary numbers. In this method, multiplying one number by a second is performed by a sequence of steps in which a value (initially the first of the two numbers) is either doubled or has the first number added back into it; the order in which these steps are to be performed is given by the binary representation of the second number. This method can be seen in use, for instance, in the Rhind Mathematical Papyrus
The Rhind Mathematical Papyrus (RMP; also designated as papyrus British Museum 10057 and pBM 10058) is one of the best known examples of ancient Egyptian mathematics. It is named after Alexander Henry Rhind, a Scottish antiquarian, who purchased ...
, which dates to around 1650 BC.
China
I Ching
The ''I Ching'' or ''Yi Jing'' (, ), usually translated ''Book of Changes'' or ''Classic of Changes'', is an ancient Chinese divination text that is among the oldest of the Chinese classics. Originally a divination manual in the Western Zh ...
'' dates from the 9th century BC in China. The binary notation in the ''I Ching'' is used to interpret its quaternary divination technique.
It is based on taoistic duality of yin and yang
Yin and yang ( and ) is a Chinese philosophical concept that describes opposite but interconnected forces. In Chinese cosmology, the universe creates itself out of a primary chaos of material energy, organized into the cycles of yin and ya ...
. Eight trigrams (Bagua) and a set of 64 hexagrams ("sixty-four" gua), analogous to the three-bit and six-bit binary numerals, were in use at least as early as the Zhou Dynasty of ancient China.
The Song Dynasty
The Song dynasty (; ; 960–1279) was an imperial dynasty of China that began in 960 and lasted until 1279. The dynasty was founded by Emperor Taizu of Song following his usurpation of the throne of the Later Zhou. The Song conquered the res ...
scholar Shao Yong
Shao Yong (; 1011–1077), courtesy name Yaofu (堯夫), named Shào Kāngjié (邵康節) was a
Chinese cosmologist, historian, philosopher, and poet who greatly influenced the development of Neo-Confucianism across China during the Song dynas ...
(1011–1077) rearranged the hexagrams in a format that resembles modern binary numbers, although he did not intend his arrangement to be used mathematically. Viewing the least significant bit
In computing, bit numbering is the convention used to identify the bit positions in a binary number.
Bit significance and indexing
In computing, the least significant bit (LSB) is the bit position in a binary integer representing the binary ...
on top of single hexagrams in Shao Yong's square
and reading along rows either from bottom right to top left with solid lines as 0 and broken lines as 1 or from top left to bottom right with solid lines as 1 and broken lines as 0 hexagrams can be interpreted as sequence from 0 to 63.
India
The Indian scholarPingala
Acharya Pingala ('; c. 3rd2nd century BCE) was an ancient Indian poet and mathematician, and the author of the ' (also called the ''Pingala-sutras''), the earliest known treatise on Sanskrit prosody.
The ' is a work of eight chapters in the l ...
(c. 2nd century BC) developed a binary system for describing prosody. He used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), making it similar to Morse code
Morse code is a method used in telecommunication to encode text characters as standardized sequences of two different signal durations, called ''dots'' and ''dashes'', or ''dits'' and ''dahs''. Morse code is named after Samuel Morse, one ...
.Binary Numbers in Ancient India/ref> They were known as ''laghu'' (light) and ''guru'' (heavy) syllables. Pingala's Hindu classic titled
Chandaḥśāstra
Acharya Pingala ('; c. 3rd2nd century BCE) was an ancient Indian poet and mathematician, and the author of the ' (also called the ''Pingala-sutras''), the earliest known treatise on Sanskrit prosody.
The ' is a work of eight chapters in the late ...
(8.23) describes the formation of a matrix in order to give a unique value to each meter. "Chandaḥśāstra" literally translates to ''science of meters'' in Sanskrit. The binary representations in Pingala's system increases towards the right, and not to the left like in the binary numbers of the modern positional notation. In Pingala's system, the numbers start from number one, and not zero. Four short syllables "0000" is the first pattern and corresponds to the value one. The numerical value is obtained by adding one to the sum of place value
Positional notation (or place-value notation, or positional numeral system) usually denotes the extension to any base of the Hindu–Arabic numeral system (or decimal system). More generally, a positional system is a numeral system in which the ...
s.
Other cultures
The residents of the island ofMangareva
Mangareva is the central and largest island of the Gambier Islands in French Polynesia. It is surrounded by smaller islands: Taravai in the southwest, Aukena and Akamaru in the southeast, and islands in the north. Mangareva has a permanent p ...
in French Polynesia
)Territorial motto: ( en, "Great Tahiti of the Golden Haze")
, anthem =
, song_type = Regional anthem
, song = "Ia Ora 'O Tahiti Nui"
, image_map = French Polynesia on the globe (French Polynesia centered).svg
, map_alt = Location of French ...
were using a hybrid binary- decimal system before 1450. Slit drum
A slit drum or slit gong is a hollow percussion instrument. In spite of the name, it is not a true drum but an idiophone, usually carved or constructed from bamboo or wood into a box with one or more slits in the top. Most slit drums have one sli ...
s with binary tones are used to encode messages across Africa and Asia.
Sets of binary combinations similar to the ''I Ching'' have also been used in traditional African divination systems such as Ifá
Ifá is a Yoruba religion and system of divination. Its literary corpus is the ''Odu Ifá''. Orunmila is identified as the Grand Priest, as he revealed divinity and prophecy to the world. Babalawos or Iyanifas use either the divining chain ...
as well as in medieval
In the history of Europe, the Middle Ages or medieval period lasted approximately from the late 5th to the late 15th centuries, similar to the post-classical period of global history. It began with the fall of the Western Roman Empire a ...
Western geomancy
Geomancy (Greek: γεωμαντεία, "earth divination") is a method of divination that interprets markings on the ground or the patterns formed by tossed handfuls of soil, rocks, or sand. The most prevalent form of divinatory geomancy in ...
.
Western predecessors to Leibniz
In the late 13th century Ramon Llull had the ambition to account for all wisdom in every branch of human knowledge of the time. For that purpose he developed a general method or 'Ars generalis' based on binary combinations of a number of simple basic principles or categories, for which he has been considered a predecessor of computing science and artificial intelligence. In 1605Francis Bacon
Francis Bacon, 1st Viscount St Alban (; 22 January 1561 – 9 April 1626), also known as Lord Verulam, was an English philosopher and statesman who served as Attorney General and Lord Chancellor of England. Bacon led the advancement of both ...
discussed a system whereby letters of the alphabet could be reduced to sequences of binary digits, which could then be encoded as scarcely visible variations in the font in any random text. Importantly for the general theory of binary encoding, he added that this method could be used with any objects at all: "provided those objects be capable of a twofold difference only; as by Bells, by Trumpets, by Lights and Torches, by the report of Muskets, and any instruments of like nature".
(See Bacon's cipher
Bacon's cipher or the Baconian cipher is a method of steganographic message encoding devised by Francis Bacon in 1605. A message is concealed in the presentation of text, rather than its content.
Cipher details
To encode a message, each letter of ...
.)
John Napier
John Napier of Merchiston (; 1 February 1550 – 4 April 1617), nicknamed Marvellous Merchiston, was a Scottish landowner known as a mathematician, physicist, and astronomer. He was the 8th Laird of Merchiston. His Latinized name was Ioa ...
in 1617 described a system he called location arithmetic
Location arithmetic (Latin ''arithmeticae localis'') is the additive (non-positional) binary numeral systems, which John Napier explored as a computation technique in his treatise '' Rabdology'' (1617), both symbolically and on a chessboard-like ...
for doing binary calculations using a non-positional representation by letters.
Thomas Harriot
Thomas Harriot (; – 2 July 1621), also spelled Harriott, Hariot or Heriot, was an English astronomer, mathematician, ethnographer and translator to whom the theory of refraction is attributed. Thomas Harriot was also recognized for his co ...
investigated several positional numbering systems, including binary, but did not publish his results; they were found later among his papers.
Possibly the first publication of the system in Europe was by Juan Caramuel y Lobkowitz
Juan Caramuel y Lobkowitz (Juan Caramuel de Lobkowitz, 23 May 1606 in Madrid — 7 or 8 September 1682 in Vigevano) was a Spanish Catholic scholastic philosopher, ecclesiastic, mathematician and writer. He is believed to be a great-grandson of J ...
, in 1700.
Leibniz and the ''I Ching''
 Leibniz studied binary numbering in 1679; his work appears in his article ''Explication de l'Arithmétique Binaire'' (published in 1703).
The full title of Leibniz's article is translated into English as the ''"Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of
Leibniz studied binary numbering in 1679; his work appears in his article ''Explication de l'Arithmétique Binaire'' (published in 1703).
The full title of Leibniz's article is translated into English as the ''"Explanation of Binary Arithmetic, which uses only the characters 1 and 0, with some remarks on its usefulness, and on the light it throws on the ancient Chinese figures of Fu Xi
Fuxi or Fu Hsi (伏羲 ~ 伏犧 ~ 伏戲) is a culture hero in Chinese legend and mythology, credited along with his sister and wife Nüwa with creating humanity and the invention of music, hunting, fishing, domestication, and cooking as well ...
"''.Leibniz G., Explication de l'Arithmétique Binaire, Die Mathematische Schriften, ed. C. Gerhardt, Berlin 1879, vol.7, p.223; Engl. trans/ref> Leibniz's system uses 0 and 1, like the modern binary numeral system. An example of Leibniz's binary numeral system is as follows: : 0 0 0 1 numerical value 20 : 0 0 1 0 numerical value 21 : 0 1 0 0 numerical value 22 : 1 0 0 0 numerical value 23 Leibniz interpreted the hexagrams of the ''I Ching'' as evidence of binary calculus. As a
Sinophile
A Sinophile is a person who demonstrates a strong interest for China, Chinese culture, Chinese language, Chinese history, and/or Chinese people.
Those with professional training and practice in the study of China are referred to as Sinolog ...
, Leibniz was aware of the ''I Ching'', noted with fascination how its hexagrams correspond to the binary numbers from 0 to 111111, and concluded that this mapping was evidence of major Chinese accomplishments in the sort of philosophical mathematics he admired. The relation was a central idea to his universal concept of a language or characteristica universalis
The Latin term ''characteristica universalis'', commonly interpreted as ''universal characteristic'', or ''universal character'' in English, is a universal and formal language imagined by Gottfried Leibniz able to express mathematical, scienti ...
, a popular idea that would be followed closely by his successors such as Gottlob Frege
Friedrich Ludwig Gottlob Frege (; ; 8 November 1848 – 26 July 1925) was a German philosopher, logician, and mathematician. He was a mathematics professor at the University of Jena, and is understood by many to be the father of analytic ph ...
and George Boole
George Boole (; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher, and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in ...
in forming modern symbolic logic.
Leibniz was first introduced to the ''I Ching
The ''I Ching'' or ''Yi Jing'' (, ), usually translated ''Book of Changes'' or ''Classic of Changes'', is an ancient Chinese divination text that is among the oldest of the Chinese classics. Originally a divination manual in the Western Zh ...
'' through his contact with the French Jesuit Joachim Bouvet
Joachim Bouvet (, courtesy name: 明远) (July 18, 1656, in Le Mans – June 28, 1730, in Peking) was a French Jesuit who worked in China, and the leading member of the Figurist movement.
China
Bouvet came to China in 1687, as one of six Jesui ...
, who visited China in 1685 as a missionary. Leibniz saw the ''I Ching'' hexagrams as an affirmation of the universality of his own religious beliefs as a Christian. Binary numerals were central to Leibniz's theology. He believed that binary numbers were symbolic of the Christian idea of ''creatio ex nihilo
(Latin for "creation out of nothing") is the doctrine that matter is not eternal but had to be created by some divine creative act. It is a theistic answer to the question of how the universe comes to exist. It is in contrast to ''Ex nihilo n ...
'' or creation out of nothing.
Later developments
 In 1854, British mathematician
In 1854, British mathematician George Boole
George Boole (; 2 November 1815 – 8 December 1864) was a largely self-taught English mathematician, philosopher, and logician, most of whose short career was spent as the first professor of mathematics at Queen's College, Cork in ...
published a landmark paper detailing an algebra
Algebra () is one of the areas of mathematics, broad areas of mathematics. Roughly speaking, algebra is the study of mathematical symbols and the rules for manipulating these symbols in formulas; it is a unifying thread of almost all of mathem ...
ic system of logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premis ...
that would become known as Boolean algebra
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas ...
. His logical calculus was to become instrumental in the design of digital electronic circuitry.
In 1937, Claude Shannon
Claude Elwood Shannon (April 30, 1916 – February 24, 2001) was an American mathematician, electrical engineer, and cryptographer known as a "father of information theory".
As a 21-year-old master's degree student at the Massachusetts In ...
produced his master's thesis at MIT
The Massachusetts Institute of Technology (MIT) is a private land-grant research university in Cambridge, Massachusetts. Established in 1861, MIT has played a key role in the development of modern technology and science, and is one of the ...
that implemented Boolean algebra and binary arithmetic using electronic relays and switches for the first time in history. Entitled ''A Symbolic Analysis of Relay and Switching Circuits
"A Symbolic Analysis of Relay and Switching Circuits" is the title of a master's thesis written by computer science pioneer Claude E. Shannon while attending the Massachusetts Institute of Technology (MIT) in 1937. In his thesis, Shannon, a dua ...
'', Shannon's thesis essentially founded practical digital circuit In theoretical computer science, a circuit is a model of computation in which input values proceed through a sequence of gates, each of which computes a function. Circuits of this kind provide a generalization of Boolean circuits and a mathematica ...
design.
In November 1937, George Stibitz
George Robert Stibitz (April 30, 1904 – January 31, 1995) was a Bell Labs researcher internationally recognized as one of the fathers of the modern digital computer. He was known for his work in the 1930s and 1940s on the realization of Boolea ...
, then working at Bell Labs
Nokia Bell Labs, originally named Bell Telephone Laboratories (1925–1984),
then AT&T Bell Laboratories (1984–1996)
and Bell Labs Innovations (1996–2007),
is an American industrial research and scientific development company owned by mult ...
, completed a relay-based computer he dubbed the "Model K" (for "Kitchen", where he had assembled it), which calculated using binary addition. Bell Labs authorized a full research program in late 1938 with Stibitz at the helm. Their Complex Number Computer, completed 8 January 1940, was able to calculate complex numbers
In mathematics, a complex number is an element of a number system that extends the real numbers with a specific element denoted , called the imaginary unit and satisfying the equation i^= -1; every complex number can be expressed in the for ...
. In a demonstration to the American Mathematical Society
The American Mathematical Society (AMS) is an association of professional mathematicians dedicated to the interests of mathematical research and scholarship, and serves the national and international community through its publications, meetings ...
conference at Dartmouth College
Dartmouth College (; ) is a private research university in Hanover, New Hampshire. Established in 1769 by Eleazar Wheelock, it is one of the nine colonial colleges chartered before the American Revolution. Although founded to educate Native ...
on 11 September 1940, Stibitz was able to send the Complex Number Calculator remote commands over telephone lines by a teletype
A teleprinter (teletypewriter, teletype or TTY) is an electromechanical device that can be used to send and receive typed messages through various communications channels, in both point-to-point and point-to-multipoint configurations. Init ...
. It was the first computing machine ever used remotely over a phone line. Some participants of the conference who witnessed the demonstration were John von Neumann
John von Neumann (; hu, Neumann János Lajos, ; December 28, 1903 – February 8, 1957) was a Hungarian-American mathematician, physicist, computer scientist, engineer and polymath. He was regarded as having perhaps the widest cove ...
, John Mauchly
John William Mauchly (August 30, 1907 – January 8, 1980) was an American physicist who, along with J. Presper Eckert, designed ENIAC, the first general-purpose electronic digital computer, as well as EDVAC, BINAC and UNIVAC I, the first ...
and Norbert Wiener
Norbert Wiener (November 26, 1894 – March 18, 1964) was an American mathematician and philosopher. He was a professor of mathematics at the Massachusetts Institute of Technology (MIT). A child prodigy, Wiener later became an early researcher ...
, who wrote about it in his memoirs.
The Z1 computer, which was designed and built by Konrad Zuse
Konrad Ernst Otto Zuse (; 22 June 1910 – 18 December 1995) was a German civil engineer, pioneering computer scientist, inventor and businessman. His greatest achievement was the world's first programmable computer; the functional program- ...
between 1935 and 1938, used Boolean logic
In mathematics and mathematical logic, Boolean algebra is a branch of algebra. It differs from elementary algebra in two ways. First, the values of the variables are the truth values ''true'' and ''false'', usually denoted 1 and 0, whereas in ...
and binary floating point number
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be r ...
s. (12 pages)
Representation
Any number can be represented by a sequence ofbit
The bit is the most basic unit of information in computing and digital communications. The name is a portmanteau of binary digit. The bit represents a logical state with one of two possible values. These values are most commonly represented a ...
s (binary digits), which in turn may be represented by any mechanism capable of being in two mutually exclusive states. Any of the following rows of symbols can be interpreted as the binary numeric value of 667:
The numeric value represented in each case is dependent upon the value assigned to each symbol. In the earlier days of computing, switches, punched holes and punched paper tapes were used to represent binary values. In a modern computer, the numeric values may be represented by two different voltage
Voltage, also known as electric pressure, electric tension, or (electric) potential difference, is the difference in electric potential between two points. In a static electric field, it corresponds to the work needed per unit of charge t ...
s; on a magnetic
Magnetism is the class of physical attributes that are mediated by a magnetic field, which refers to the capacity to induce attractive and repulsive phenomena in other entities. Electric currents and the magnetic moments of elementary particles ...
disk, magnetic polarities may be used. A "positive", " yes", or "on" state is not necessarily equivalent to the numerical value of one; it depends on the architecture in use.
In keeping with customary representation of numerals using Arabic numerals
Arabic numerals are the ten numerical digits: , , , , , , , , and . They are the most commonly used symbols to write decimal numbers. They are also used for writing numbers in other systems such as octal, and for writing identifiers such as ...
, binary numbers are commonly written using the symbols 0 and 1. When written, binary numerals are often subscripted, prefixed or suffixed in order to indicate their base, or radix. The following notations are equivalent:
* 100101 binary (explicit statement of format)
* 100101b (a suffix indicating binary format; also known as Intel convention
In computing, endianness, also known as byte sex, is the order or sequence of bytes of a word of digital data in computer memory. Endianness is primarily expressed as big-endian (BE) or little-endian (LE). A big-endian system stores the most sig ...
)
* 100101B (a suffix indicating binary format)
* bin 100101 (a prefix indicating binary format)
* 1001012 (a subscript indicating base-2 (binary) notation)
* %100101 (a prefix indicating binary format; also known as Motorola convention
In computing, endianness, also known as byte sex, is the order or sequence of bytes of a word of digital data in computer memory. Endianness is primarily expressed as big-endian (BE) or little-endian (LE). A big-endian system stores the most sig ...
)
* 0b100101 (a prefix indicating binary format, common in programming languages)
* 6b100101 (a prefix indicating number of bits in binary format, common in programming languages)
* #b100101 (a prefix indicating binary format, common in Lisp programming languages)
When spoken, binary numerals are usually read digit-by-digit, in order to distinguish them from decimal numerals. For example, the binary numeral 100 is pronounced ''one zero zero'', rather than ''one hundred'', to make its binary nature explicit, and for purposes of correctness. Since the binary numeral 100 represents the value four, it would be confusing to refer to the numeral as ''one hundred'' (a word that represents a completely different value, or amount). Alternatively, the binary numeral 100 can be read out as "four" (the correct ''value''), but this does not make its binary nature explicit.
Counting in binary
Counting in binary is similar to counting in any other number system. Beginning with a single digit, counting proceeds through each symbol, in increasing order. Before examining binary counting, it is useful to briefly discuss the more familiar decimal counting system as a frame of reference.Decimal counting
Decimal counting uses the ten symbols ''0'' through ''9''. Counting begins with the incremental substitution of the least significant digit (rightmost digit) which is often called the ''first digit''. When the available symbols for this position are exhausted, the least significant digit is reset to ''0'', and the next digit of higher significance (one position to the left) is incremented (''overflow''), and incremental substitution of the low-order digit resumes. This method of reset and overflow is repeated for each digit of significance. Counting progresses as follows: :000, 001, 002, ... 007, 008, 009, (rightmost digit is reset to zero, and the digit to its left is incremented) :010, 011, 012, ... : ... :090, 091, 092, ... 097, 098, 099, (rightmost two digits are reset to zeroes, and next digit is incremented) :100, 101, 102, ...Binary counting

Fractions
Fractions in binary arithmetic terminate only if 2 is the onlyprime factor
A prime number (or a prime) is a natural number greater than 1 that is not a product of two smaller natural numbers. A natural number greater than 1 that is not prime is called a composite number. For example, 5 is prime because the only ways ...
in the denominator
A fraction (from la, fractus, "broken") represents a part of a whole or, more generally, any number of equal parts. When spoken in everyday English, a fraction describes how many parts of a certain size there are, for example, one-half, eight ...
. As a result, 1/10 does not have a finite binary representation (10 has prime factors 2 and 5). This causes 10 × 0.1 not to precisely equal 1 in floating-point arithmetic
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can b ...
. As an example, to interpret the binary expression for 1/3 = .010101..., this means: 1/3 = 0 × 2−1 + 1 × 2−2 + 0 × 2−3 + 1 × 2−4 + ... = 0.3125 + ... An exact value cannot be found with a sum of a finite number of inverse powers of two, the zeros and ones in the binary representation of 1/3 alternate forever.
Binary arithmetic
Arithmetic
Arithmetic () is an elementary part of mathematics that consists of the study of the properties of the traditional operations on numbers—addition, subtraction, multiplication, division, exponentiation, and extraction of roots. In the 19th c ...
in binary is much like arithmetic in other numeral systems. Addition, subtraction, multiplication, and division can be performed on binary numerals.
Addition
The simplest arithmetic operation in binary is addition. Adding two single-digit binary numbers is relatively simple, using a form of carrying: :0 + 0 → 0 :0 + 1 → 1 :1 + 0 → 1 :1 + 1 → 0, carry 1 (since 1 + 1 = 2 = 0 + (1 × 21) ) Adding two "1" digits produces a digit "0", while 1 will have to be added to the next column. This is similar to what happens in decimal when certain single-digit numbers are added together; if the result equals or exceeds the value of the radix (10), the digit to the left is incremented: :5 + 5 → 0, carry 1 (since 5 + 5 = 10 = 0 + (1 × 101) ) :7 + 9 → 6, carry 1 (since 7 + 9 = 16 = 6 + (1 × 101) ) This is known as ''carrying''. When the result of an addition exceeds the value of a digit, the procedure is to "carry" the excess amount divided by the radix (that is, 10/10) to the left, adding it to the next positional value. This is correct since the next position has a weight that is higher by a factor equal to the radix. Carrying works the same way in binary: 0 1 1 0 1 + 1 0 1 1 1 ------------- = 1 0 0 1 0 0 = 36 In this example, two numerals are being added together: 011012 (1310) and 101112 (2310). The top row shows the carry bits used. Starting in the rightmost column, 1 + 1 = 102. The 1 is carried to the left, and the 0 is written at the bottom of the rightmost column. The second column from the right is added: 1 + 0 + 1 = 102 again; the 1 is carried, and 0 is written at the bottom. The third column: 1 + 1 + 1 = 112. This time, a 1 is carried, and a 1 is written in the bottom row. Proceeding like this gives the final answer 1001002 (3610). When computers must add two numbers, the rule that: xxor
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , , ...
y = (x + y) mod 2
for any two bits x and y allows for very fast calculation, as well.
Long carry method
A simplification for many binary addition problems is the "long carry method" or "Brookhouse Method of Binary Addition". This method is particularly when one of the numbers contains a long stretch of ones. It is based on the simple premise that under the binary system, when given a stretch of digits composed entirely of ones (where is any integer length), adding 1 will result in the number 1 followed by a string of zeros. That concept follows, logically, just as in the decimal system, where adding 1 to a string of 9s will result in the number 1 followed by a string of 0s: Binary Decimal 1 1 1 1 1 likewise 9 9 9 9 9 + 1 + 1 ——————————— ——————————— 1 0 0 0 0 0 1 0 0 0 0 0 Such long strings are quite common in the binary system. From that one finds that large binary numbers can be added using two simple steps, without excessive carry operations. In the following example, two numerals are being added together: 1 1 1 0 1 1 1 1 1 02 (95810) and 1 0 1 0 1 1 0 0 1 12 (69110), using the traditional carry method on the left, and the long carry method on the right: Traditional Carry Method Long Carry Method vs. carry the 1 until it is one digit past the "string" below 1 1 1 0 1 1 1 1 1 0Addition table
The binary addition table is similar, but not the same, as thetruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra (logic), Boolean algebra, boolean functions, and propositional calculus—which sets out the functional values of logical expression (mathematics) ...
of the logical disjunction
In logic, disjunction is a logical connective typically notated as \lor and read aloud as "or". For instance, the English language sentence "it is raining or it is snowing" can be represented in logic using the disjunctive formula R \lor ...
operation . The difference is that , while .
Subtraction
Subtraction
Subtraction is an arithmetic operation that represents the operation of removing objects from a collection. Subtraction is signified by the minus sign, . For example, in the adjacent picture, there are peaches—meaning 5 peaches with 2 taken ...
works in much the same way:
:0 − 0 → 0
:0 − 1 → 1, borrow 1
:1 − 0 → 1
:1 − 1 → 0
Subtracting a "1" digit from a "0" digit produces the digit "1", while 1 will have to be subtracted from the next column. This is known as ''borrowing''. The principle is the same as for carrying. When the result of a subtraction is less than 0, the least possible value of a digit, the procedure is to "borrow" the deficit divided by the radix (that is, 10/10) from the left, subtracting it from the next positional value.
* * * * (starred columns are borrowed from)
1 1 0 1 1 1 0
− 1 0 1 1 1
----------------
= 1 0 1 0 1 1 1
* (starred columns are borrowed from)
1 0 1 1 1 1 1
- 1 0 1 0 1 1
----------------
= 0 1 1 0 1 0 0
Subtracting a positive number is equivalent to ''adding'' a negative number
In mathematics, a negative number represents an opposite. In the real number system, a negative number is a number that is inequality (mathematics), less than 0 (number), zero. Negative numbers are often used to represent the magnitude of a loss ...
of equal absolute value. Computers use signed number representations
In computing, signed number representations are required to encode negative numbers in binary number systems.
In mathematics, negative numbers in any base are represented by prefixing them with a minus sign ("−"). However, in RAM or CPU regi ...
to handle negative numbers—most commonly the two's complement
Two's complement is a mathematical operation to reversibly convert a positive binary number into a negative binary number with equivalent (but negative) value, using the binary digit with the greatest place value (the leftmost bit in big- endian ...
notation. Such representations eliminate the need for a separate "subtract" operation. Using two's complement notation subtraction can be summarized by the following formula:
:
Multiplication
Multiplication
Multiplication (often denoted by the cross symbol , by the mid-line dot operator , by juxtaposition, or, on computers, by an asterisk ) is one of the four elementary mathematical operations of arithmetic, with the other ones being ad ...
in binary is similar to its decimal counterpart. Two numbers and can be multiplied by partial products: for each digit in , the product of that digit in is calculated and written on a new line, shifted leftward so that its rightmost digit lines up with the digit in that was used. The sum of all these partial products gives the final result.
Since there are only two digits in binary, there are only two possible outcomes of each partial multiplication:
* If the digit in is 0, the partial product is also 0
* If the digit in is 1, the partial product is equal to
For example, the binary numbers 1011 and 1010 are multiplied as follows:
1 0 1 1 ()
× 1 0 1 0 ()
---------
0 0 0 0 ← Corresponds to the rightmost 'zero' in
+ 1 0 1 1 ← Corresponds to the next 'one' in
+ 0 0 0 0
+ 1 0 1 1
---------------
= 1 1 0 1 1 1 0
Binary numbers can also be multiplied with bits after a binary point
A decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form (e.g., "." in 12.45). Different countries officially designate different symbols for use as the separator. The cho ...
:
1 0 1 . 1 0 1 (5.625 in decimal)
× 1 1 0 . 0 1 (6.25 in decimal)
-------------------
1 . 0 1 1 0 1 ← Corresponds to a 'one' in
+ 0 0 . 0 0 0 0 ← Corresponds to a 'zero' in
+ 0 0 0 . 0 0 0
+ 1 0 1 1 . 0 1
+ 1 0 1 1 0 . 1
---------------------------
= 1 0 0 0 1 1 . 0 0 1 0 1 (35.15625 in decimal)
See also Booth's multiplication algorithm
Booth's multiplication algorithm is a multiplication algorithm that multiplies two signed binary numbers in two's complement notation. The algorithm was invented by Andrew Donald Booth in 1950 while doing research on crystallography at Birkbeck Co ...
.
Multiplication table
The binary multiplication table is the same as thetruth table
A truth table is a mathematical table used in logic—specifically in connection with Boolean algebra (logic), Boolean algebra, boolean functions, and propositional calculus—which sets out the functional values of logical expression (mathematics) ...
of the logical conjunction
In logic, mathematics and linguistics, And (\wedge) is the truth-functional operator of logical conjunction; the ''and'' of a set of operands is true if and only if ''all'' of its operands are true. The logical connective that represents thi ...
operation .
Division
Long division
In arithmetic, long division is a standard division algorithm suitable for dividing multi-digit Hindu-Arabic numerals ( Positional notation) that is simple enough to perform by hand. It breaks down a division problem into a series of easier steps ...
in binary is again similar to its decimal counterpart.
In the example below, the divisor
In mathematics, a divisor of an integer n, also called a factor of n, is an integer m that may be multiplied by some integer to produce n. In this case, one also says that n is a multiple of m. An integer n is divisible or evenly divisible by ...
is 1012, or 5 in decimal, while the dividend
A dividend is a distribution of profits by a corporation to its shareholders. When a corporation earns a profit or surplus, it is able to pay a portion of the profit as a dividend to shareholders. Any amount not distributed is taken to be re-inv ...
is 110112, or 27 in decimal. The procedure is the same as that of decimal long division
In arithmetic, long division is a standard division algorithm suitable for dividing multi-digit Hindu-Arabic numerals ( Positional notation) that is simple enough to perform by hand. It breaks down a division problem into a series of easier steps ...
; here, the divisor 1012 goes into the first three digits 1102 of the dividend one time, so a "1" is written on the top line. This result is multiplied by the divisor, and subtracted from the first three digits of the dividend; the next digit (a "1") is included to obtain a new three-digit sequence:
1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
0 0 1
The procedure is then repeated with the new sequence, continuing until the digits in the dividend have been exhausted:
1 0 1
___________
1 0 1 ) 1 1 0 1 1
− 1 0 1
-----
1 1 1
− 1 0 1
-----
0 1 0
Thus, the quotient
In arithmetic, a quotient (from lat, quotiens 'how many times', pronounced ) is a quantity produced by the division of two numbers. The quotient has widespread use throughout mathematics, and is commonly referred to as the integer part of a ...
of 110112 divided by 1012 is 1012, as shown on the top line, while the remainder, shown on the bottom line, is 102. In decimal, this corresponds to the fact that 27 divided by 5 is 5, with a remainder of 2.
Aside from long division, one can also devise the procedure so as to allow for over-subtracting from the partial remainder at each iteration, thereby leading to alternative methods which are less systematic, but more flexible as a result.
Square root
The process of taking a binary square root digit by digit is the same as for a decimal square root and is explainedhere
Here is an adverb that means "in, on, or at this place". It may also refer to:
Software
* Here Technologies, a mapping company
* Here WeGo (formerly Here Maps), a mobile app and map website by Here
Television
* Here TV (formerly "here!"), a ...
. An example is:
1 0 0 1
---------
√ 1010001
1
---------
101 01
0
--------
1001 100
0
--------
10001 10001
10001
-------
0
Bitwise operations
Though not directly related to the numerical interpretation of binary symbols, sequences of bits may be manipulated using Boolean logical operators. When a string of binary symbols is manipulated in this way, it is called abitwise operation
In computer programming, a bitwise operation operates on a bit string, a bit array or a binary numeral (considered as a bit string) at the level of its individual bits. It is a fast and simple action, basic to the higher-level arithmetic ope ...
; the logical operators AND
or AND may refer to:
Logic, grammar, and computing
* Conjunction (grammar), connecting two words, phrases, or clauses
* Logical conjunction in mathematical logic, notated as "∧", "⋅", "&", or simple juxtaposition
* Bitwise AND, a bool ...
, OR, and XOR
Exclusive or or exclusive disjunction is a logical operation that is true if and only if its arguments differ (one is true, the other is false).
It is symbolized by the prefix operator J and by the infix operators XOR ( or ), EOR, EXOR, , , ...
may be performed on corresponding bits in two binary numerals provided as input. The logical NOT operation may be performed on individual bits in a single binary numeral provided as input. Sometimes, such operations may be used as arithmetic short-cuts, and may have other computational benefits as well. For example, an arithmetic shift
In computer programming, an arithmetic shift is a shift operator, sometimes termed a signed shift (though it is not restricted to signed operands). The two basic types are the arithmetic left shift and the arithmetic right shift. For binary ...
left of a binary number is the equivalent of multiplication by a (positive, integral) power of 2.
Conversion to and from other numeral systems
Decimal to Binary
 To convert from a base-10
To convert from a base-10 integer
An integer is the number zero (), a positive natural number (, , , etc.) or a negative integer with a minus sign ( −1, −2, −3, etc.). The negative numbers are the additive inverses of the corresponding positive numbers. In the language ...
to its base-2 (binary) equivalent, the number is divided by two. The remainder is the least-significant bit
In computing, bit numbering is the convention used to identify the bit positions in a binary number.
Bit significance and indexing
In computing, the least significant bit (LSB) is the bit position in a binary integer representing the binary ...
. The quotient is again divided by two; its remainder becomes the next least significant bit. This process repeats until a quotient of one is reached. The sequence of remainders (including the final quotient of one) forms the binary value, as each remainder must be either zero or one when dividing by two. For example, (357)10 is expressed as (101100101)2.
Binary to Decimal
Conversion from base-2 to base-10 simply inverts the preceding algorithm. The bits of the binary number are used one by one, starting with the most significant (leftmost) bit. Beginning with the value 0, the prior value is doubled, and the next bit is then added to produce the next value. This can be organized in a multi-column table. For example, to convert 100101011012 to decimal: The result is 119710. The first Prior Value of 0 is simply an initial decimal value. This method is an application of theHorner scheme
In mathematics and computer science, Horner's method (or Horner's scheme) is an algorithm for polynomial evaluation. Although named after William George Horner, this method is much older, as it has been attributed to Joseph-Louis Lagrange by Hor ...
.
The fractional parts of a number are converted with similar methods. They are again based on the equivalence of shifting with doubling or halving.
In a fractional binary number such as 0.110101101012, the first digit is , the second , etc. So if there is a 1 in the first place after the decimal, then the number is at least , and vice versa. Double that number is at least 1. This suggests the algorithm: Repeatedly double the number to be converted, record if the result is at least 1, and then throw away the integer part.
For example, , in binary, is:
Thus the repeating decimal fraction 0.... is equivalent to the repeating binary fraction 0.... .
Or for example, 0.110, in binary, is:
This is also a repeating binary fraction 0.0... . It may come as a surprise that terminating decimal fractions can have repeating expansions in binary. It is for this reason that many are surprised to discover that 0.1 + ... + 0.1, (10 additions) differs from 1 in floating point arithmetic
In computing, floating-point arithmetic (FP) is arithmetic that represents real numbers approximately, using an integer with a fixed precision, called the significand, scaled by an integer exponent of a fixed base. For example, 12.345 can be r ...
. In fact, the only binary fractions with terminating expansions are of the form of an integer divided by a power of 2, which 1/10 is not.
The final conversion is from binary to decimal fractions. The only difficulty arises with repeating fractions, but otherwise the method is to shift the fraction to an integer, convert it as above, and then divide by the appropriate power of two in the decimal base. For example:
Another way of converting from binary to decimal, often quicker for a person familiar with hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, h ...
, is to do so indirectly—first converting ( in binary) into ( in hexadecimal) and then converting ( in hexadecimal) into ( in decimal).
For very large numbers, these simple methods are inefficient because they perform a large number of multiplications or divisions where one operand is very large. A simple divide-and-conquer algorithm is more effective asymptotically: given a binary number, it is divided by 10''k'', where ''k'' is chosen so that the quotient roughly equals the remainder; then each of these pieces is converted to decimal and the two are concatenated
In formal language theory and computer programming, string concatenation is the operation of joining character strings end-to-end. For example, the concatenation of "snow" and "ball" is "snowball". In certain formalisations of concatenatio ...
. Given a decimal number, it can be split into two pieces of about the same size, each of which is converted to binary, whereupon the first converted piece is multiplied by 10''k'' and added to the second converted piece, where ''k'' is the number of decimal digits in the second, least-significant piece before conversion.
Hexadecimal
Binary may be converted to and from hexadecimal more easily. This is because the radix of the hexadecimal system (16) is a power of the radix of the binary system (2). More specifically, 16 = 24, so it takes four digits of binary to represent one digit of hexadecimal, as shown in the adjacent table. To convert a hexadecimal number into its binary equivalent, simply substitute the corresponding binary digits: :3A16 = 0011 10102 :E716 = 1110 01112 To convert a binary number into its hexadecimal equivalent, divide it into groups of four bits. If the number of bits isn't a multiple of four, simply insert extra 0 bits at the left (calledpadding
Padding is thin cushioned material sometimes added to clothes. Padding may also be referred to as batting when used as a layer in lining quilts or as a packaging or stuffing material. When padding is used in clothes, it is often done in an attempt ...
). For example:
:10100102 = 0101 0010 grouped with padding = 5216
:110111012 = 1101 1101 grouped = DD16
To convert a hexadecimal number into its decimal equivalent, multiply the decimal equivalent of each hexadecimal digit by the corresponding power of 16 and add the resulting values:
:C0E716 = (12 × 163) + (0 × 162) + (14 × 161) + (7 × 160) = (12 × 4096) + (0 × 256) + (14 × 16) + (7 × 1) = 49,38310
Octal
Binary is also easily converted to theoctal
The octal numeral system, or oct for short, is the radix, base-8 number system, and uses the Numerical digit, digits 0 to 7. This is to say that 10octal represents eight and 100octal represents sixty-four. However, English, like most languages, ...
numeral system, since octal uses a radix of 8, which is a power of two
A power of two is a number of the form where is an integer, that is, the result of exponentiation with number two as the base and integer as the exponent.
In a context where only integers are considered, is restricted to non-negati ...
(namely, 23, so it takes exactly three binary digits to represent an octal digit). The correspondence between octal and binary numerals is the same as for the first eight digits of hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, h ...
in the table above. Binary 000 is equivalent to the octal digit 0, binary 111 is equivalent to octal 7, and so forth.
Converting from octal to binary proceeds in the same fashion as it does for hexadecimal
In mathematics and computing, the hexadecimal (also base-16 or simply hex) numeral system is a positional numeral system that represents numbers using a radix (base) of 16. Unlike the decimal system representing numbers using 10 symbols, h ...
:
:658 = 110 1012
:178 = 001 1112
And from binary to octal:
:1011002 = 101 1002 grouped = 548
:100112 = 010 0112 grouped with padding = 238
And from octal to decimal:
:658 = (6 × 81) + (5 × 80) = (6 × 8) + (5 × 1) = 5310
:1278 = (1 × 82) + (2 × 81) + (7 × 80) = (1 × 64) + (2 × 8) + (7 × 1) = 8710
Representing real numbers
Non-integers can be represented by using negative powers, which are set off from the other digits by means of aradix point
A decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form (e.g., "." in 12.45). Different countries officially designate different symbols for use as the separator. The cho ...
(called a decimal point
A decimal separator is a symbol used to separate the integer part from the fractional part of a number written in decimal form (e.g., "." in 12.45). Different countries officially designate different symbols for use as the separator. The ch ...
in the decimal system). For example, the binary number 11.012 means:
For a total of 3.25 decimal.
All dyadic rational numbers have a ''terminating'' binary numeral—the binary representation has a finite number of terms after the radix point. Other rational numbers
In mathematics, a rational number is a number that can be expressed as the quotient or fraction of two integers, a numerator and a non-zero denominator . For example, is a rational number, as is every integer (e.g. ). The set of all r ...
have binary representation, but instead of terminating, they ''recur'', with a finite sequence of digits repeating indefinitely. For instance
The phenomenon that the binary representation of any rational is either terminating or recurring also occurs in other radix-based numeral systems. See, for instance, the explanation in decimal. Another similarity is the existence of alternative representations for any terminating representation, relying on the fact that 0.111111... is the sum of the geometric series
In mathematics, a geometric series is the sum of an infinite number of terms that have a constant ratio between successive terms. For example, the series
:\frac \,+\, \frac \,+\, \frac \,+\, \frac \,+\, \cdots
is geometric, because each su ...
2−1 + 2−2 + 2−3 + ... which is 1.
Binary numerals which neither terminate nor recur represent irrational number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two inte ...
s. For instance,
* 0.10100100010000100000100... does have a pattern, but it is not a fixed-length recurring pattern, so the number is irrational
* 1.0110101000001001111001100110011111110... is the binary representation of , the square root of 2
The square root of 2 (approximately 1.4142) is a positive real number that, when multiplied by itself, equals the number 2. It may be written in mathematics as \sqrt or 2^, and is an algebraic number. Technically, it should be called the princi ...
, another irrational. It has no discernible pattern.
See also
*Balanced ternary
Balanced ternary is a ternary numeral system (i.e. base 3 with three digits) that uses a balanced signed-digit representation of the integers in which the digits have the values −1, 0, and 1. This stands in contrast to the standard (unbalanc ...
* Binary code
A binary code represents text, computer processor instructions, or any other data using a two-symbol system. The two-symbol system used is often "0" and "1" from the binary number system. The binary code assigns a pattern of binary digits, als ...
* Binary-coded decimal
In computing and electronic systems, binary-coded decimal (BCD) is a class of binary encodings of decimal numbers where each digit is represented by a fixed number of bits, usually four or eight. Sometimes, special bit patterns are used fo ...
* Finger binary
Finger binary is a system for counting and displaying binary numbers on the fingers of either or both hands. Each finger represents one binary digit or bit. This allows counting from zero to 31 using the fingers of one hand, or 1023 using both: t ...
* Gray code
The reflected binary code (RBC), also known as reflected binary (RB) or Gray code after Frank Gray, is an ordering of the binary numeral system such that two successive values differ in only one bit (binary digit).
For example, the representat ...
* IEEE 754
The IEEE Standard for Floating-Point Arithmetic (IEEE 754) is a technical standard for floating-point arithmetic established in 1985 by the Institute of Electrical and Electronics Engineers (IEEE). The standard addressed many problems found i ...
* Linear-feedback shift register
In computing, a linear-feedback shift register (LFSR) is a shift register whose input bit is a linear function of its previous state.
The most commonly used linear function of single bits is exclusive-or (XOR). Thus, an LFSR is most often a ...
* Offset binary
Offset binary, also referred to as excess-K, excess-''N'', excess-e, excess code or biased representation, is a method for signed number representation where a signed number n is represented by the bit pattern corresponding to the unsigned numbe ...
* Quibinary
Bi-quinary coded decimal is a numeral encoding scheme used in many abacuses and in some early computers, including the Colossus. The term ''bi-quinary'' indicates that the code comprises both a two-state (''bi'') and a five-state (''quin''ary) ...
* Reduction of summands
Reduction of summands is an algorithm for fast binary multiplication of non-signed binary integers. It is performed in three steps: production of summands, reduction of summands, and summation.
Steps Production of summands
In binary multiplicatio ...
* Redundant binary representation A redundant binary representation (RBR) is a numeral system that uses more bits than needed to represent a single binary digit so that most numbers have several representations. An RBR is unlike usual binary numeral systems, including two's complem ...
* Repeating decimal
A repeating decimal or recurring decimal is decimal representation of a number whose digits are periodic (repeating its values at regular intervals) and the infinitely repeated portion is not zero. It can be shown that a number is rational i ...
* Two's complement
Two's complement is a mathematical operation to reversibly convert a positive binary number into a negative binary number with equivalent (but negative) value, using the binary digit with the greatest place value (the leftmost bit in big- endian ...
References
External links
Binary System
at cut-the-knot
Conversion of Fractions
at cut-the-knot
Sir Francis Bacon's BiLiteral Cypher system
predates binary number system. {{Authority control Binary arithmetic Computer arithmetic Elementary arithmetic Gottfried Wilhelm Leibniz Power-of-two numeral systems