|
Pingala
Acharya Pingala (; c. 3rd2nd century BCE) was an ancient Indian poet and mathematician, and the author of the ' (), also called the ''Pingala-sutras'' (), the earliest known treatise on Sanskrit prosody. The ' is a work of eight chapters in the late Sūtra style, not fully comprehensible without a commentary. It has been dated to the last few centuries BCE. In the 10th century CE, Halayudha wrote a commentary elaborating on the '. According to some historians Maharshi Pingala was the brother of Pāṇini, the famous Sanskrit grammarian, considered the first descriptive linguist''. François & Ponsonnet (2013: 184).'' Another think tank identifies him as Patanjali, the 2nd century CE scholar who authored Mahabhashya. Combinatorics The ' presents a formula to generate systematic enumerations of metres, of all possible combinations of light (''laghu'') and heavy (''guru'') syllables, for a word of ''n'' syllables, using a recursive formula, that results in a partially ordered ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chandas
Sanskrit prosody or Chandas refers to one of the six Vedangas, or limbs of Vedic studies.James Lochtefeld (2002), "Chandas" in The Illustrated Encyclopedia of Hinduism, Vol. 1: A-M, Rosen Publishing, , page 140 It is the study of poetic metres and verse in Sanskrit. This field of study was central to the composition of the Vedas, the scriptural canons of Hinduism; in fact, so central that some later Hindu and Buddhist texts refer to the Vedas as ''Chandas''. The Chandas, as developed by the Vedic schools, were organized around seven major metres, each with its own rhythm, movements and aesthetics. Sanskrit metres include those based on a fixed number of syllables per verse, and those based on fixed number of morae per verse. Extant ancient manuals on Chandas include Pingala's ''Chandah Sutra'', while an example of a medieval Sanskrit prosody manual is Kedara Bhatta's ''Vrittaratnakara''. The most exhaustive compilations of Sanskrit prosody describe over 600 metres. This is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sanskrit Prosody
Sanskrit prosody or Chandas refers to one of the six Vedangas, or limbs of Vedic studies.James Lochtefeld (2002), "Chandas" in The Illustrated Encyclopedia of Hinduism, Vol. 1: A-M, Rosen Publishing, , page 140 It is the study of poetic metres and verse in Sanskrit. This field of study was central to the composition of the Vedas, the scriptural canons of Hinduism; in fact, so central that some later Hindu and Buddhist texts refer to the Vedas as ''Chandas''. The Chandas, as developed by the Vedic schools, were organized around seven major metres, each with its own rhythm, movements and aesthetics. Sanskrit metres include those based on a fixed number of syllables per verse, and those based on fixed number of morae per verse. Extant ancient manuals on Chandas include Pingala's ''Chandah Sutra'', while an example of a medieval Sanskrit prosody manual is Kedara Bhatta's ''Vrittaratnakara''. The most exhaustive compilations of Sanskrit prosody describe over 600 metres. This i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Number
In mathematics, the Fibonacci sequence is a Integer sequence, sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 and some (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the sequence begins : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The Fibonacci numbers were first described in Indian mathematics as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book . Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the ''Fibonacci Quarterly''. Appli ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fibonacci Numbers
In mathematics, the Fibonacci sequence is a sequence in which each element is the sum of the two elements that precede it. Numbers that are part of the Fibonacci sequence are known as Fibonacci numbers, commonly denoted . Many writers begin the sequence with 0 and 1, although some authors start it from 1 and 1 and some (as did Fibonacci) from 1 and 2. Starting from 0 and 1, the sequence begins : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, ... The Fibonacci numbers were first described in Indian mathematics as early as 200 BC in work by Pingala on enumerating possible patterns of Sanskrit poetry formed from syllables of two lengths. They are named after the Italian mathematician Leonardo of Pisa, also known as Fibonacci, who introduced the sequence to Western European mathematics in his 1202 book . Fibonacci numbers appear unexpectedly often in mathematics, so much so that there is an entire journal dedicated to their study, the '' Fibonacci Quarterly''. Applications of Fibon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indian Mathematics
Indian mathematics emerged in the Indian subcontinent from 1200 BCE until the end of the 18th century. In the classical period of Indian mathematics (400 CE to 1200 CE), important contributions were made by scholars like Aryabhata, Brahmagupta, Bhaskara II, Varāhamihira, and Madhava of Sangamagrama, Madhava. The Decimal, decimal number system in use today: "The measure of the genius of Indian civilisation, to which we owe our modern (number) system, is all the greater in that it was the only one in all history to have achieved this triumph. Some cultures succeeded, earlier than the Indian, in discovering one or at best two of the characteristics of this intellectual feat. But none of them managed to bring together into a complete and coherent system the necessary and sufficient conditions for a number-system with the same potential as our own." was first recorded in Indian mathematics. Indian mathematicians made early contributions to the study of the concept of 0 (number), ze ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
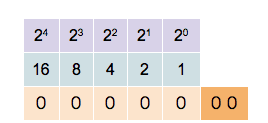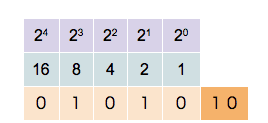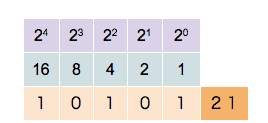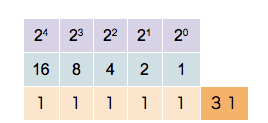
Binary Number
A binary number is a number expressed in the Radix, base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computer, computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thoma ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Numbers
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" (zero) and "1" (one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harriot, an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binary Numeral System
A binary number is a number expressed in the base-2 numeral system or binary numeral system, a method for representing numbers that uses only two symbols for the natural numbers: typically "0" ( zero) and "1" ( one). A ''binary number'' may also refer to a rational number that has a finite representation in the binary numeral system, that is, the quotient of an integer by a power of two. The base-2 numeral system is a positional notation with a radix of 2. Each digit is referred to as a bit, or binary digit. Because of its straightforward implementation in digital electronic circuitry using logic gates, the binary system is used by almost all modern computers and computer-based devices, as a preferred system of use, over various other human techniques of communication, because of the simplicity of the language and the noise immunity in physical implementation. History The modern binary number system was studied in Europe in the 16th and 17th centuries by Thomas Harrio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Binomial Theorem
In elementary algebra, the binomial theorem (or binomial expansion) describes the algebraic expansion of powers of a binomial. According to the theorem, the power expands into a polynomial with terms of the form , where the exponents and are nonnegative integers satisfying and the coefficient of each term is a specific positive integer depending on and . For example, for , (x+y)^4 = x^4 + 4 x^3y + 6 x^2 y^2 + 4 x y^3 + y^4. The coefficient in each term is known as the binomial coefficient or (the two have the same value). These coefficients for varying and can be arranged to form Pascal's triangle. These numbers also occur in combinatorics, where gives the number of different combinations (i.e. subsets) of elements that can be chosen from an -element set. Therefore is usually pronounced as " choose ". Statement According to the theorem, the expansion of any nonnegative integer power of the binomial is a sum of the form (x+y)^n = x^n y^0 + x^ y^1 + x^ y^ ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pāṇini
(; , ) was a Sanskrit grammarian, logician, philologist, and revered scholar in ancient India during the mid-1st millennium BCE, dated variously by most scholars between the 6th–5th and 4th century BCE. The historical facts of his life are unknown, except only what can be inferred from his works, and legends recorded long after. His most notable work, the ''Aṣṭādhyāyī,'' is conventionally taken to mark the start of Classical Sanskrit. His work formally codified Classical Sanskrit as a refined and standardized language, making use of a technical metalanguage consisting of a syntax, morphology, and lexicon, organised according to a series of meta-rules. Since the exposure of European scholars to his ''Aṣṭādhyāyī'' in the nineteenth century, Pāṇini has been considered the "first Descriptive linguistics, descriptive linguist",#FPencyclo, François & Ponsonnet (2013: 184). and even labelled as "the father of linguistics". His approach to grammar influenced such ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Halayudha
Halāyudha (Sanskrit: हलायुध) wrote the ', a commentary on Pingala's ''Chandaḥśāstra'', was an Indian Mathematician and poet who lived and worked in the 10th century. The '' Chandaḥśāstra'' by the Indian lyricist Piṅgala (3rd or 2nd century BC) somewhat crypically describes a method of arranging two types of syllables to form metres of various lengths and counting them; as interpreted and elaborated by Halāyudha his "method of pyramidal expansion" (''meru-prastāra'') for counting metres is equivalent to Pascal's triangle. Biography Halayudha originally resided at the Rashtrakuta capital Manyakheta, where he wrote under the patronage of emperor Krishna III. His ''Kavi-Rahasya'' eulogizes Krishna III. Later, he migrated to Ujjain in the Paramara kingdom. There, he composed ''Mṛta-Sañjīvanī'' in honour of the Paramara king Munja. Works Halayudha composed the following works: * ''Kavi-Rahasya'', a book on poetics * ''Mṛta-Sañjīvanī'', ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Indian Mathematicians
Indian mathematicians have made a number of contributions to mathematics that have significantly influenced scientists and mathematicians in the modern era. One of such works is Hindu numeral system which is predominantly used today and is likely to be used in the future. Ancient (Before 320 CE) *Shulba sutras (around 1st millenium BCE) * Baudhayana sutras (fl. c. 900 BCE) *Yajnavalkya (700 BCE) *Manava (fl. 750–650 BCE) *Apastamba Dharmasutra (c. 600 BCE) *''Pāṇini'' (c. 520–460 BCE) * Kātyāyana (fl. c. 300 BCE) *Nyāya Sūtras, Akṣapada Gautama(c. 600 BCE–200 CE) *Bharata Muni (200 BCE-200 CE) *Pingala (c. 3rd/2nd century BCE) * Bhadrabahu (367 – 298 BCE) * Umasvati (c. 200 CE) * Yavaneśvara, Yavaneśvara (2nd century) * Vasishtha Siddhanta, 4th century CE Classical (320 CE–520 CE) *Vasishtha Siddhanta, 4th century CE * Aryabhata (476–550 CE) * Yativrsabha (500–570) * Varahamihira (505–587 CE) * Yativṛṣabha, (6th-century CE) * Virahanka (6th cent ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |