Binary Octahedral Group

In mathematics, the binary octahedral group, name as 2O or Coxeter&Moser: Generators and Relations for discrete groups: : R^l = S^m = Tⁿ = RST is a certain nonabelian group of order 48. It is an extension of the chiral octahedral group ''O'' or (2,3,4) of order 24 by a cyclic group of order 2, and is the preimage of the octahedral group under the 2:1 covering homomorphism $\operatorname(3) \to \operatorname(3)$ of the special orthogonal group by the spin group. It follows that the binary octahedral group is a discrete subgroup of Spin(3) of order 48.

The binary octahedral group is most easily described concretely as a discrete subgroup of the unit quaternions, under the isomorphism $\operatorname(3) \cong \operatorname(1)$ where Sp(1) is the multiplicative group of unit quaternions. (For a description of this homomorphism see the article on quaternions and spatial rotations.)

Elements

Explicitly, the binary octahedral group is given as the union of the 24 Hurwitz units
:$\$
with all 24 quaternions obtained from
:$\tfrac(\pm 1 \pm 1i + 0j + 0k)$
by a permutation of coordinates and all possible sign combinations. All 48 elements have absolute value 1 and therefore lie in the unit quaternion group Sp(1).

Properties

The binary octahedral group, denoted by 2''O'', fits into the short exact sequence
:$1\to\\to 2O\to O \to 1.\,$
This sequence does not split, meaning that 2''O'' is ''not'' a semidirect product of by ''O''. In fact, there is no subgroup of 2''O'' isomorphic to ''O''.

The center of 2''O'' is the subgroup , so that the inner automorphism group is isomorphic to ''O''. The full automorphism group is isomorphic to ''O'' × Z₂.

Presentation

The group 2''O'' has a presentation given by
:$\langle r,s,t \mid r^2 = s^3 = t^4 = rst \rangle$
or equivalently,
:$\langle s,t \mid (st)^2 = s^3 = t^4 \rangle.$
Quaternion generators with these relations are given by
:$r = \tfrac(i+j) \qquad s = \tfrac(1+i+j+k) \qquad t = \tfrac(1+i),$

with $r^2 = s^3 = t^4 = rst = -1.$

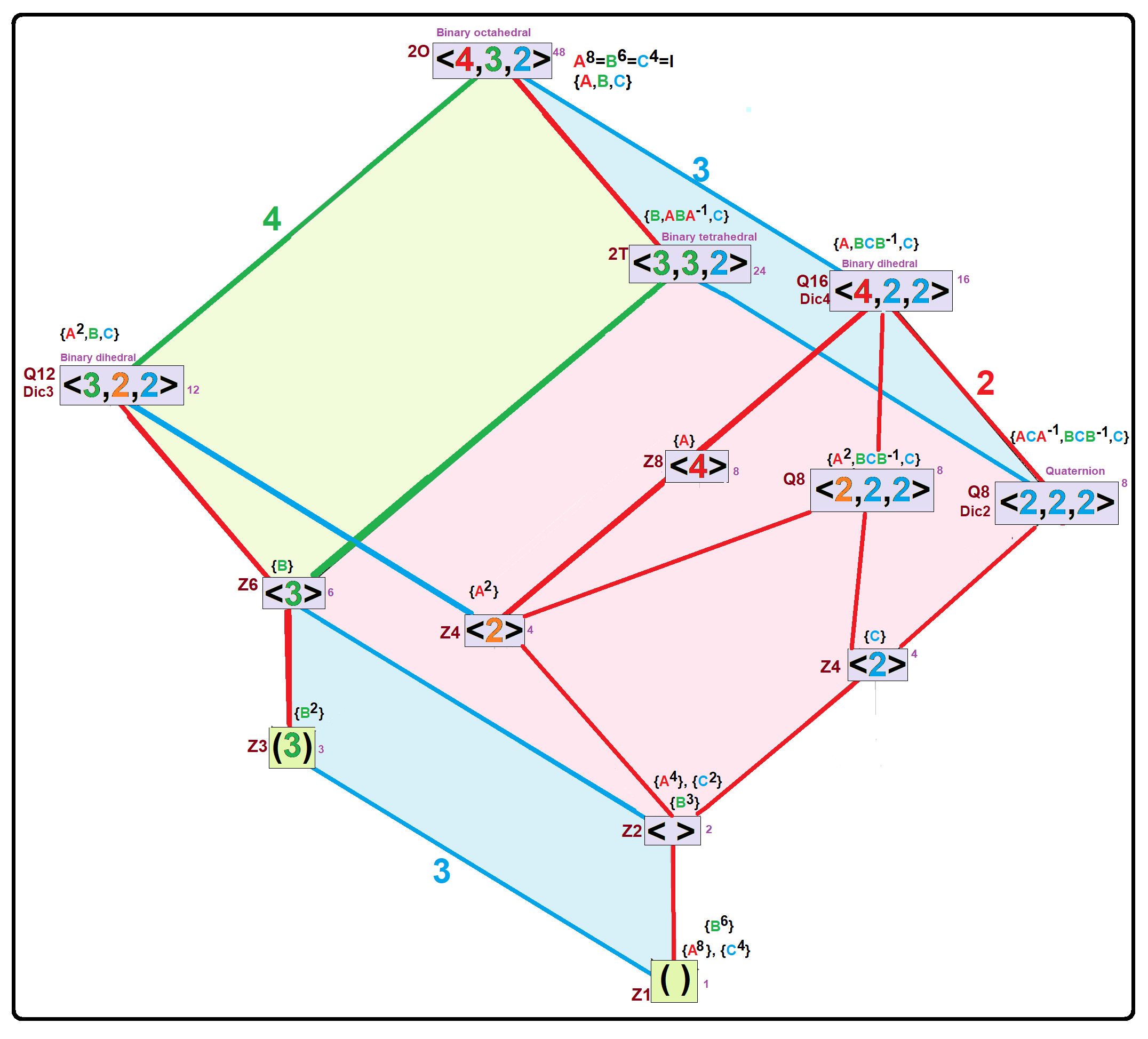
Subgroups

The binary tetrahedral group, 2''T'', consisting of the 24 Hurwitz units, forms a normal subgroup of index 2. The quaternion group, ''Q''8, consisting of the 8 Lipschitz units forms a normal subgroup of 2''O'' of index 6. The quotient group is isomorphic to ''S''₃ (the symmetric group on 3 letters). These two groups, together with the center , are the only nontrivial normal subgroups of 2''O''.

The generalized quaternion group, ''Q''16, also forms a subgroup of 2''O'', index 3. This subgroup is self-normalizing so its conjugacy class has 3 members. There are also isomorphic copies of the binary dihedral groups ''Q''8 and ''Q''12 in 2''O''.

All other subgroups are cyclic groups generated by the various elements (with orders 3, 4, 6, and 8).Binary octahedral group = $CSU_2(\mathbb F_3)$ o
GroupNames
/ref>

Higher dimensions

The ''binary octahedral group'' generalizes to higher dimensions: just as the octahedron generalizes to the orthoplex, the octahedral group in SO(3) generalizes to the hyperoctahedral group in SO(''n''), which has a binary cover under the map $\operatorname(n) \to SO(n).$

See also

* Binary polyhedral group
* binary cyclic group, ⟨''n''⟩, index 2''n''
* binary dihedral group, ⟨2,2,''n''⟩, index 4''n''
*binary tetrahedral group, 2T=⟨2,3,3⟩, index 24
*binary icosahedral group, 2I=⟨2,3,5⟩, index 120

References

*
*

Notes

{{reflist

Octahedral