5-simplex T01234 on:
[Wikipedia]
[Google]
[Amazon]
In
3,2,3, order 72. It represents joining of 2 orthogonal triangles, orthogonally offset, with all pairs of vertices connected between.
The form ∨∨ has symmetry [2,2,2, order 48.
These are seen in the
3,3,3,3 symmetry, order 1440. The intersection of these two 5-simplexes is a uniform 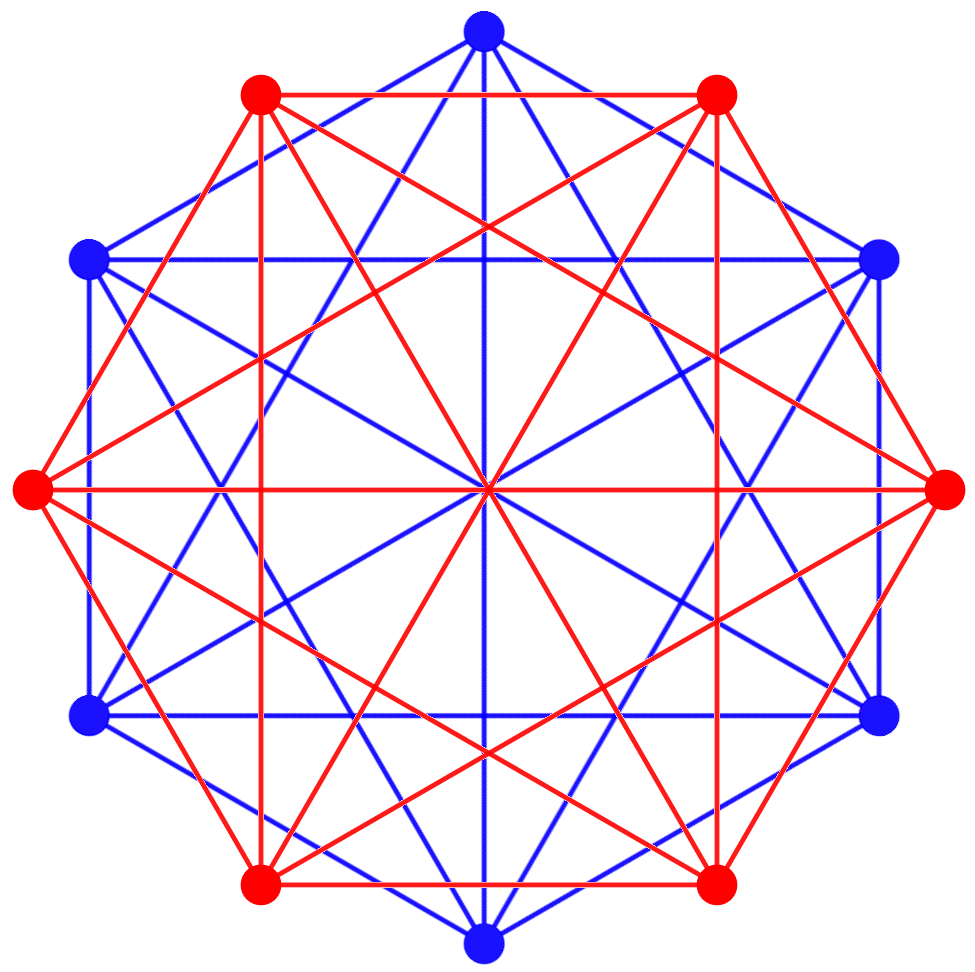
Polytopes of Various Dimensions
Jonathan Bowers
{{Polytopes 5-polytopes
five-dimensional
A five-dimensional space is a space with five dimensions. In mathematics, a sequence of ''N'' numbers can represent a location in an ''N''-dimensional space. If interpreted physically, that is one more than the usual three spatial dimensions a ...
geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is c ...
, a 5-simplex
In geometry, a simplex (plural: simplexes or simplices) is a generalization of the notion of a triangle or tetrahedron to arbitrary dimensions. The simplex is so-named because it represents the simplest possible polytope in any given dimension. ...
is a self-dual regular 5-polytope
In geometry, a five-dimensional polytope (or 5-polytope) is a polytope in five-dimensional space, bounded by (4-polytope) facets, pairs of which share a polyhedral cell.
Definition
A 5-polytope is a closed five-dimensional figure with vertices ...
. It has six vertices, 15 edges, 20 triangle faces, 15 tetrahedral cells
Cell most often refers to:
* Cell (biology), the functional basic unit of life
Cell may also refer to:
Locations
* Monastic cell, a small room, hut, or cave in which a religious recluse lives, alternatively the small precursor of a monastery w ...
, and 6 5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
facets. It has a dihedral angle of cos−1(), or approximately 78.46°.
The 5-simplex is a solution to the problem: ''Make 20 equilateral triangles using 15 matchsticks, where each side of every triangle is exactly one matchstick.''
Alternate names
It can also be called a hexateron, or hexa-5-tope, as a 6- facetted polytope in 5-dimensions. Thename
A name is a term used for identification by an external observer. They can identify a class or category of things, or a single thing, either uniquely, or within a given context. The entity identified by a name is called its referent. A personal ...
''hexateron'' is derived from ''hexa-'' for having six facets and '' teron'' (with ''ter-'' being a corruption of ''tetra-
Numeral or number prefixes are prefixes derived from numerals or occasionally other numbers. In English and many other languages, they are used to coin numerous series of words. For example:
* unicycle, bicycle, tricycle (1-cycle, 2-cycle, 3-cyc ...
'') for having four-dimensional facets.
By Jonathan Bowers, a hexateron is given the acronym hix.
As a configuration
This configuration matrix represents the 5-simplex. The rows and columns correspond to vertices, edges, faces, cells and 4-faces. The diagonal numbers say how many of each element occur in the whole 5-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.Regular hexateron cartesian coordinates
The ''hexateron'' can be constructed from a5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
by adding a 6th vertex such that it is equidistant from all the other vertices of the 5-cell.
The Cartesian coordinates
A Cartesian coordinate system (, ) in a plane is a coordinate system that specifies each point uniquely by a pair of numerical coordinates, which are the signed distances to the point from two fixed perpendicular oriented lines, measured in t ...
for the vertices of an origin-centered regular hexateron having edge length 2 are:
:
The vertices of the ''5-simplex'' can be more simply positioned on a hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
in 6-space as permutations of (0,0,0,0,0,1) ''or'' (0,1,1,1,1,1). These construction can be seen as facets of the 6-orthoplex or rectified 6-cube respectively.
Projected images
Lower symmetry forms
A lower symmetry form is a ''5-cell pyramid'' ( )v, with ,3,3symmetry order 120, constructed as a5-cell
In geometry, the 5-cell is the convex 4-polytope with Schläfli symbol . It is a 5-vertex four-dimensional object bounded by five tetrahedral cells. It is also known as a C5, pentachoron, pentatope, pentahedroid, or tetrahedral pyramid. It i ...
base in a 4-space hyperplane
In geometry, a hyperplane is a subspace whose dimension is one less than that of its ''ambient space''. For example, if a space is 3-dimensional then its hyperplanes are the 2-dimensional planes, while if the space is 2-dimensional, its hyper ...
, and an apex point ''above'' the hyperplane. The five ''sides'' of the pyramid are made of 5-cell cells. These are seen as vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s of truncated regular 6-polytope
In six-dimensional geometry, a six-dimensional polytope or 6-polytope is a polytope, bounded by 5-polytope facets.
Definition
A 6-polytope is a closed six-dimensional figure with vertices, edges, faces, cells (3-faces), 4-faces, and 5-faces. A ...
s, like a truncated 6-cube
In six-dimensional geometry, a truncated 6-cube (or truncated hexeract) is a convex uniform 6-polytope, being a truncation of the regular 6-cube.
There are 5 truncations for the 6-cube. Vertices of the truncated 6-cube are located as pairs on the ...
.
Another form is ∨, with ,3,3symmetry order 48, the joining of an orthogonal digon and a tetrahedron, orthogonally offset, with all pairs of vertices connected between. Another form is ∨, with ,2,3
The comma is a punctuation mark that appears in several variants in different languages. It has the same shape as an apostrophe or single closing quotation mark () in many typefaces, but it differs from them in being placed on the baseline ...
symmetry order 36, and extended symmetry vertex figure
In geometry, a vertex figure, broadly speaking, is the figure exposed when a corner of a polyhedron or polytope is sliced off.
Definitions
Take some corner or Vertex (geometry), vertex of a polyhedron. Mark a point somewhere along each connect ...
s of bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube">Bitruncation">bitruncated and tritruncated regular 6-polytopes, like a bitruncated 6-cube and a tritruncated 6-simplex. The edge labels here represent the types of face along that direction, and thus represent different edge lengths.
The vertex figure of the omnitruncated 5-simplex honeycomb, , is a 5-simplx with a petrie polygon cycle of 5 long edges.
Compound
The compound of two 5-simplexes in dual configurations can be seen in this A6 Coxeter plane projection, with a red and blue 5-simplex vertices and edges. This compound hasbirectified 5-simplex
In five-dimensional geometry, a rectified 5-simplex is a convex uniform 5-polytope, being a Rectification (geometry), rectification of the regular 5-simplex.
There are three unique degrees of rectifications, including the zeroth, the 5-simplex its ...
. = ∩ .
:
Related uniform 5-polytopes
It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 13k series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedralhosohedron
In spherical geometry, an -gonal hosohedron is a tessellation of lunes on a spherical surface, such that each lune shares the same two polar opposite vertices.
A regular -gonal hosohedron has Schläfli symbol with each spherical lune havin ...
.
It is first in a dimensional series of uniform polytopes and honeycombs, expressed by Coxeter as 3k1 series. A degenerate 4-dimensional case exists as 3-sphere tiling, a tetrahedral dihedron
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of ''n'' edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat ...
.
The 5-simplex, as 220 polytope is first in dimensional series 22k.
The regular 5-simplex is one of 19 uniform polytera based on the ,3,3,3 Coxeter group, all shown here in A5 Coxeter plane orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Two-dimensional space, two dimensions. Orthographic projection is a form of parallel projection in ...
s. (Vertices are colored by projection overlap order, red, orange, yellow, green, cyan, blue, purple having progressively more vertices)
See also
*11-cell
In mathematics, the 11-cell (or hendecachoron) is a self-dual abstract regular 4-polytope ( four-dimensional polytope). Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. It has Schläfli symbol , with 3 hemi-icosahedr ...
Notes
References
* * Coxeter, H.S.M.: ** ** *** (Paper 22) *** (Paper 23) *** (Paper 24) * * **External links
*Polytopes of Various Dimensions
Jonathan Bowers
{{Polytopes 5-polytopes