|
Vector Optimization
Vector optimization is a subarea of mathematical optimization where Optimization problem, optimization problems with a vector-valued objective functions are optimized with respect to a given partial ordering and subject to certain constraints. A multi-objective optimization problem is a special case of a vector optimization problem: The objective space is the finite dimensional Euclidean space partially ordered by the component-wise "less than or equal to" ordering. Problem formulation In mathematical terms, a vector optimization problem can be written as: :C\operatorname\min_ f(x) where f: X \to Z for a partially ordered vector space Z. The partial ordering is induced by a cone C \subseteq Z. X is an arbitrary set and S \subseteq X is called the feasible set. Solution concepts There are different minimality notions, among them: * \bar \in S is a ''weakly efficient point'' (weak minimizer) if for every x \in S one has f(x) - f(\bar) \not\in -\operatorname C. * \bar \in S is an ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematical Optimization
Mathematical optimization (alternatively spelled ''optimisation'') or mathematical programming is the selection of a best element, with regard to some criterion, from some set of available alternatives. It is generally divided into two subfields: discrete optimization and continuous optimization. Optimization problems of sorts arise in all quantitative disciplines from computer science and engineering to operations research and economics, and the development of solution methods has been of interest in mathematics for centuries. In the more general approach, an optimization problem consists of maxima and minima, maximizing or minimizing a Function of a real variable, real function by systematically choosing Argument of a function, input values from within an allowed set and computing the Value (mathematics), value of the function. The generalization of optimization theory and techniques to other formulations constitutes a large area of applied mathematics. More generally, opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Optimization Problem
In mathematics, computer science and economics, an optimization problem is the problem of finding the ''best'' solution from all feasible solutions. Optimization problems can be divided into two categories, depending on whether the variables are continuous or discrete: * An optimization problem with discrete variables is known as a ''discrete optimization'', in which an object such as an integer, permutation or graph must be found from a countable set. * A problem with continuous variables is known as a ''continuous optimization'', in which an optimal value from a continuous function must be found. They can include constrained problems and multimodal problems. Continuous optimization problem The '' standard form'' of a continuous optimization problem is \begin &\underset& & f(x) \\ &\operatorname & &g_i(x) \leq 0, \quad i = 1,\dots,m \\ &&&h_j(x) = 0, \quad j = 1, \dots,p \end where * is the objective function to be minimized over the -variable vector , * are called ine ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
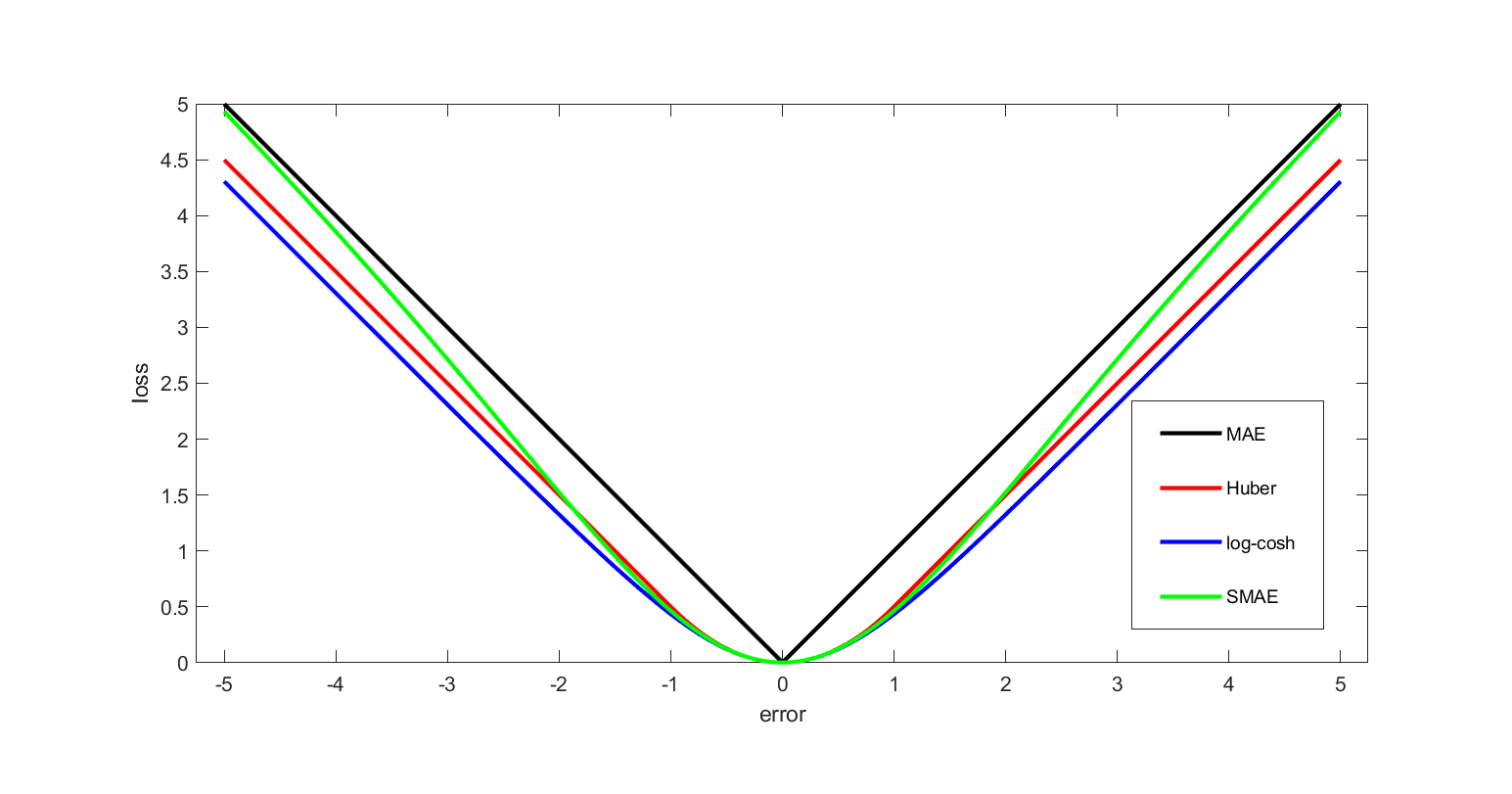
Objective Function
In mathematical optimization and decision theory, a loss function or cost function (sometimes also called an error function) is a function that maps an event or values of one or more variables onto a real number intuitively representing some "cost" associated with the event. An optimization problem seeks to minimize a loss function. An objective function is either a loss function or its opposite (in specific domains, variously called a reward function, a profit function, a utility function, a fitness function, etc.), in which case it is to be maximized. The loss function could include terms from several levels of the hierarchy. In statistics, typically a loss function is used for parameter estimation, and the event in question is some function of the difference between estimated and true values for an instance of data. The concept, as old as Laplace, was reintroduced in statistics by Abraham Wald in the middle of the 20th century. In the context of economics, for example, this ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Ordering
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''incompara ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Multi-objective Optimization
Multi-objective optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, multiattribute optimization or Pareto optimization) is an area of multiple criteria decision making that is concerned with mathematical optimization problems involving more than one objective function to be optimized simultaneously. Multi-objective optimization has been applied in many fields of science, including engineering, economics and logistics where optimal decisions need to be taken in the presence of trade-offs between two or more conflicting objectives. Minimizing cost while maximizing comfort while buying a car, and maximizing performance whilst minimizing fuel consumption and emission of pollutants of a vehicle are examples of multi-objective optimization problems involving two and three objectives, respectively. In practical problems, there can be more than three objectives. For a nontrivial multi-objective optimization problem, no single solutio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Vector Space
In mathematics and physics, a vector space (also called a linear space) is a set whose elements, often called ''vectors'', may be added together and multiplied ("scaled") by numbers called '' scalars''. Scalars are often real numbers, but can be complex numbers or, more generally, elements of any field. The operations of vector addition and scalar multiplication must satisfy certain requirements, called ''vector axioms''. The terms real vector space and complex vector space are often used to specify the nature of the scalars: real coordinate space or complex coordinate space. Vector spaces generalize Euclidean vectors, which allow modeling of physical quantities, such as forces and velocity, that have not only a magnitude, but also a direction. The concept of vector spaces is fundamental for linear algebra, together with the concept of matrix, which allows computing in vector spaces. This provides a concise and synthetic way for manipulating and studying systems of linear eq ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Closure (mathematics)
In mathematics, a subset of a given set is closed under an operation of the larger set if performing that operation on members of the subset always produces a member of that subset. For example, the natural numbers are closed under addition, but not under subtraction: is not a natural number, although both 1 and 2 are. Similarly, a subset is said to be closed under a ''collection'' of operations if it is closed under each of the operations individually. The closure of a subset is the result of a closure operator applied to the subset. The ''closure'' of a subset under some operations is the smallest subset that is closed under these operations. It is often called the ''span'' (for example linear span) or the ''generated set''. Definitions Let be a set equipped with one or several methods for producing elements of from other elements of . Operations and (partial) multivariate function are examples of such methods. If is a topological space, the limit of a sequence of element ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Convex Cone
In linear algebra, a ''cone''—sometimes called a linear cone for distinguishing it from other sorts of cones—is a subset of a vector space that is closed under scalar multiplication; that is, is a cone if x\in C implies sx\in C for every . When the scalars are real numbers, or belong to an ordered field, one generally calls a cone a subset of a vector space that is closed under multiplication by a ''positive scalar''. In this context, a convex cone is a cone that is closed under addition, or, equivalently, a subset of a vector space that is closed under linear combinations with positive coefficients. It follows that convex cones are convex sets. In this article, only the case of scalars in an ordered field is considered. Definition A subset ''C'' of a vector space ''V'' over an ordered field ''F'' is a cone (or sometimes called a linear cone) if for each ''x'' in ''C'' and positive scalar ''α'' in ''F'', the product ''αx'' is in ''C''. Note that some authors define co ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Infimum
In mathematics, the infimum (abbreviated inf; plural infima) of a subset S of a partially ordered set P is a greatest element in P that is less than or equal to each element of S, if such an element exists. Consequently, the term ''greatest lower bound'' (abbreviated as ) is also commonly used. The supremum (abbreviated sup; plural suprema) of a subset S of a partially ordered set P is the least element in P that is greater than or equal to each element of S, if such an element exists. Consequently, the supremum is also referred to as the ''least upper bound'' (or ). The infimum is in a precise sense dual to the concept of a supremum. Infima and suprema of real numbers are common special cases that are important in analysis, and especially in Lebesgue integration. However, the general definitions remain valid in the more abstract setting of order theory where arbitrary partially ordered sets are considered. The concepts of infimum and supremum are close to minimum and maxim ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Benson's Algorithm
Benson's algorithm, named after Harold Benson, is a method for solving multi-objective linear programming problems and vector linear programs. This works by finding the "efficient extreme points in the outcome set". The primary concept in Benson's algorithm is to evaluate the upper image of the vector optimization problem by cutting planes. Idea of algorithm Consider a vector linear program :\min_C Px \; \text A x \geq b for P \in \mathbb^, A \in \mathbb^, b \in \mathbb^m and a polyhedral convex ordering cone C having nonempty interior and containing no lines. The feasible set is S=\. In particular, Benson's algorithm finds the extreme points of the set P + C, which is called upper image. In case of C=\mathbb^q_+:=\, one obtains the special case of a multi-objective linear program (multiobjective optimization Multi-objective optimization (also known as multi-objective programming, vector optimization, multicriteria optimization, multiattribute optimization or Pareto opti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthant
In geometry, an orthant or hyperoctant is the analogue in ''n''-dimensional Euclidean space of a quadrant in the plane or an octant in three dimensions. In general an orthant in ''n''-dimensions can be considered the intersection of ''n'' mutually orthogonal half-spaces. By independent selections of half-space signs, there are 2''n'' orthants in ''n''-dimensional space. More specifically, a closed orthant in R''n'' is a subset defined by constraining each Cartesian coordinate to be nonnegative or nonpositive. Such a subset is defined by a system of inequalities: :ε1''x''1 ≥ 0 ε2''x''2 ≥ 0 · · · ε''n''''x''''n'' ≥ 0, where each ε''i'' is +1 or −1. Similarly, an open orthant in R''n'' is a subset defined by a system of strict inequalities :ε1''x''1 > 0 ε2''x''2 > 0 · ·&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
