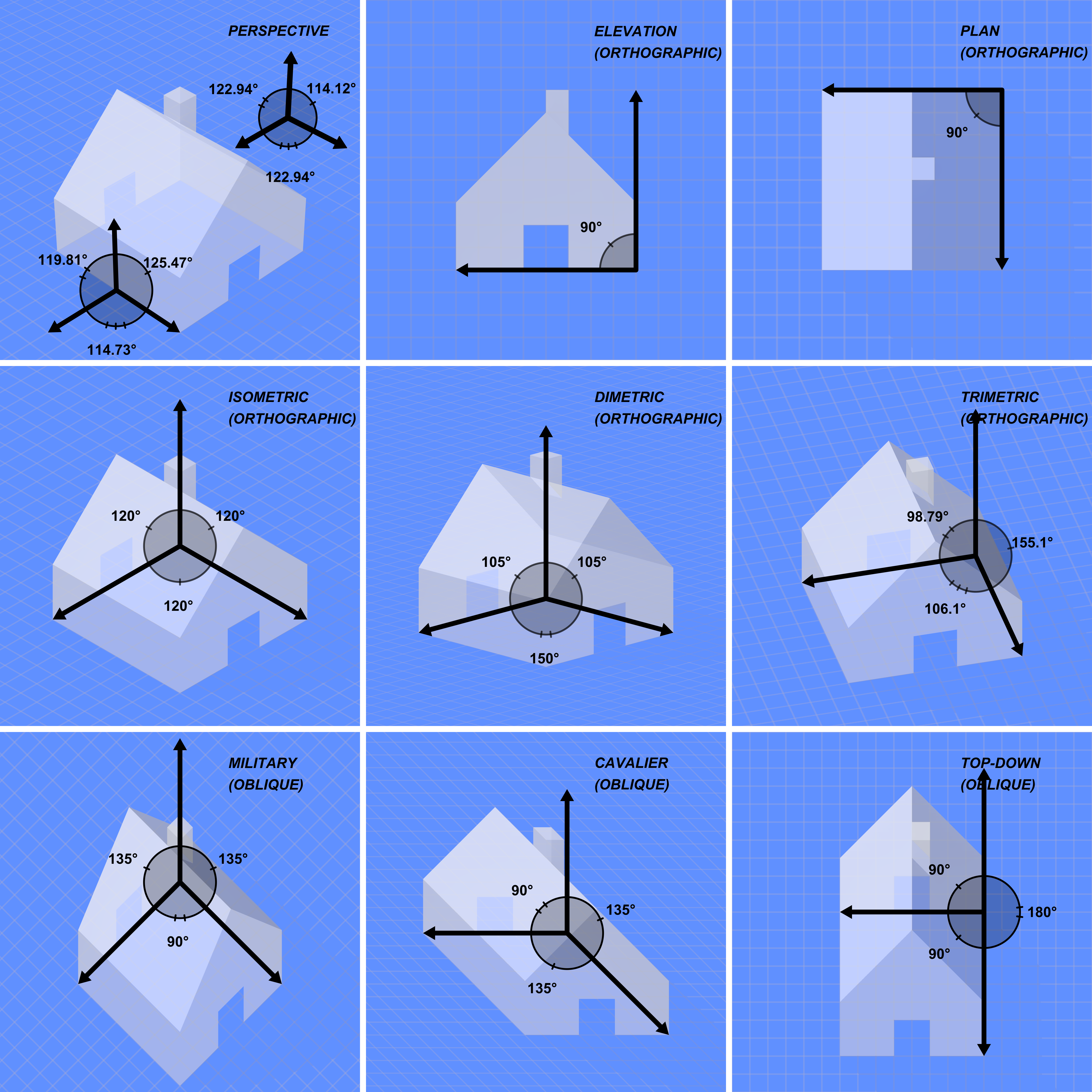
|
True Length
In geometry, true length is any distance between points that is not foreshortened by the view type.Manual of Engineering Drawing 2009, , pp. 81–85 In a three-dimensional Euclidean space, lines with true length are parallel to the projection plane. For example, in a top view of a pyramid, which is an orthographic projection, the base edges (which are parallel to the projection plane) have true length, whereas the remaining edges in this view are not true lengths. The same is true with an orthographic side view of a pyramid. If any face of a pyramid was parallel to the projection plane A projection plane, or plane of projection, is a type of view in which graphical projections from an object intersect.Gary R. Bertoline et al. (2002) ''Technical Graphics Communication''. McGraw–Hill Professional, 2002. , p. 330. Projection plane ... (for a particular view), all edges would demonstrate true length. Examples of views in which all edges have true length are nets. References ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Dodecahedron Flat
In geometry, a dodecahedron (Greek , from ''dōdeka'' "twelve" + ''hédra'' "base", "seat" or "face") or duodecahedron is any polyhedron with twelve flat faces. The most familiar dodecahedron is the regular dodecahedron with regular pentagons as faces, which is a Platonic solid. There are also three regular star dodecahedra, which are constructed as stellations of the convex form. All of these have icosahedral symmetry, order 120. Some dodecahedra have the same combinatorial structure as the regular dodecahedron (in terms of the graph formed by its vertices and edges), but their pentagonal faces are not regular: The pyritohedron, a common crystal form in pyrite, has pyritohedral symmetry, while the tetartoid has tetrahedral symmetry. The rhombic dodecahedron can be seen as a limiting case of the pyritohedron, and it has octahedral symmetry. The elongated dodecahedron and trapezo-rhombic dodecahedron variations, along with the rhombic dodecahedra, are space-filling. There a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Geometry
Geometry (; ) is, with arithmetic, one of the oldest branches of mathematics. It is concerned with properties of space such as the distance, shape, size, and relative position of figures. A mathematician who works in the field of geometry is called a ''geometer''. Until the 19th century, geometry was almost exclusively devoted to Euclidean geometry, which includes the notions of point, line, plane, distance, angle, surface, and curve, as fundamental concepts. During the 19th century several discoveries enlarged dramatically the scope of geometry. One of the oldest such discoveries is Carl Friedrich Gauss' ("remarkable theorem") that asserts roughly that the Gaussian curvature of a surface is independent from any specific embedding in a Euclidean space. This implies that surfaces can be studied ''intrinsically'', that is, as stand-alone spaces, and has been expanded into the theory of manifolds and Riemannian geometry. Later in the 19th century, it appeared that geometries ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Parallel (geometry)
In geometry, parallel lines are coplanar straight lines that do not intersect at any point. Parallel planes are planes in the same three-dimensional space that never meet. ''Parallel curves'' are curves that do not touch each other or intersect and keep a fixed minimum distance. In three-dimensional Euclidean space, a line and a plane that do not share a point are also said to be parallel. However, two noncoplanar lines are called ''skew lines''. Parallel lines are the subject of Euclid's parallel postulate. Parallelism is primarily a property of affine geometries and Euclidean geometry is a special instance of this type of geometry. In some other geometries, such as hyperbolic geometry, lines can have analogous properties that are referred to as parallelism. Symbol The parallel symbol is \parallel. For example, AB \parallel CD indicates that line ''AB'' is parallel to line ''CD''. In the Unicode character set, the "parallel" and "not parallel" signs have codepoint ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projection Plane
A projection plane, or plane of projection, is a type of view in which graphical projections from an object intersect.Gary R. Bertoline et al. (2002) ''Technical Graphics Communication''. McGraw–Hill Professional, 2002. , p. 330. Projection planes are used often in descriptive geometry and graphical representation. A picture plane in perspective drawing is a type of projection plane. With perspective drawing, the lines of sight, or projection lines, between an object and a picture plane return to a vanishing point and are not parallel. With parallel projection the lines of sight from the object to the projection plane are parallel. File:Perspective projection of triangle ABC on plane Πfrom point S.svg , Perspective projection of triangle ABC on plane Πfrom point S. File:Axonometric_projection.svg , Axonometric projection on projection plane ΠFile:Perspectiva-1.svg , A cube in two-point perspective File:Perspectiva-2.svg , Simulated rays of light travel from the object, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pyramid (geometry)
In geometry, a pyramid () is a polyhedron formed by connecting a polygonal base and a point, called the apex. Each base edge and apex form a triangle, called a ''lateral face''. It is a conic solid with polygonal base. A pyramid with an base has vertices, faces, and edges. All pyramids are self-dual. A right pyramid has its apex directly above the centroid of its base. Nonright pyramids are called oblique pyramids. A regular pyramid has a regular polygon base and is usually implied to be a ''right pyramid''. When unspecified, a pyramid is usually assumed to be a ''regular'' square pyramid, like the physical pyramid structures. A triangle-based pyramid is more often called a tetrahedron. Among oblique pyramids, like acute and obtuse triangles, a pyramid can be called ''acute'' if its apex is above the interior of the base and ''obtuse'' if its apex is above the exterior of the base. A right-angled pyramid has its apex above an edge or vertex of the base. In a tetrahedro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection (geometry)
Orthographic projection (also orthogonal projection and analemma) is a means of representing three-dimensional objects in two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Axonometric projection'' is synonymous with ''par ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Base (geometry)
In geometry, a base is a side of a polygon or a face of a polyhedron, particularly one oriented perpendicular to the direction in which height is measured, or on what is considered to be the "bottom" of the figure. This term is commonly applied to triangles, parallelograms, trapezoids, cylinders, cones, pyramids, parallelepipeds and frustums. Role in area and volume calculation Bases are commonly used (together with heights) to calculate the areas and volumes of figures. In speaking about these processes, the measure (length or area) of a figure's base is often referred to as its "base." By this usage, the area of a parallelogram or the volume of a prism or cylinder can be calculated by multiplying its "base" by its height; likewise, the areas of triangles and the volumes of cones and pyramids are fractions of the products of their bases and heights. Some figures have two parallel bases (such as trapezoids and frustums), both of which are used to calculate the extent of the figu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edge (geometry)
In geometry, an edge is a particular type of line segment joining two vertices in a polygon, polyhedron, or higher-dimensional polytope. In a polygon, an edge is a line segment on the boundary, and is often called a polygon side. In a polyhedron or more generally a polytope, an edge is a line segment where two faces (or polyhedron sides) meet. A segment joining two vertices while passing through the interior or exterior is not an edge but instead is called a diagonal. Relation to edges in graphs In graph theory, an edge is an abstract object connecting two graph vertices, unlike polygon and polyhedron edges which have a concrete geometric representation as a line segment. However, any polyhedron can be represented by its skeleton or edge-skeleton, a graph whose vertices are the geometric vertices of the polyhedron and whose edges correspond to the geometric edges. Conversely, the graphs that are skeletons of three-dimensional polyhedra can be characterized by Steinitz's theore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Side View
Side or Sides may refer to: Geometry * Edge (geometry) of a polygon (two-dimensional shape) * Face (geometry) of a polyhedron (three-dimensional shape) Places * Side (Ainis), a town of Ainis, ancient Thessaly, Greece * Side (Caria), a town of ancient Caria, Anatolia * Side (Laconia), a town of ancient Laconia, Greece * Side (Pontus), a town of ancient Pontus, Anatolia * Side, Turkey, a city in Turkey * Side, Iran, a village in Iran * Side, Gloucestershire, or Syde, a village in England Music * Side (recording), the A-side or B-side of a record * The Side, a Scottish rock band * ''Sides'' (album), a 1979 album by Anthony Phillips * ''Sides'', a 2020 album by Emily King * "Side" (song), a 2001 song by Travis * "Sides", a song by Flobots from the album ''The Circle in the Square'', 2012 * "Sides", a song by Allday from the album ''Speeding'', 2017 Teams * Side (cue sports technique) * Side, a team, in particular: ** Sports team Other uses * Side (mythology), one of three m ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Net (polyhedron)
In geometry, a net of a polyhedron is an arrangement of non-overlapping edge-joined polygons in the plane which can be folded (along edges) to become the faces of the polyhedron. Polyhedral nets are a useful aid to the study of polyhedra and solid geometry in general, as they allow for physical models of polyhedra to be constructed from material such as thin cardboard. An early instance of polyhedral nets appears in the works of Albrecht DĂĽrer, whose 1525 book ''A Course in the Art of Measurement with Compass and Ruler'' (''Unterweysung der Messung mit dem Zyrkel und Rychtscheyd '') included nets for the Platonic solids and several of the Archimedean solids. These constructions were first called nets in 1543 by Augustin Hirschvogel. Existence and uniqueness Many different nets can exist for a given polyhedron, depending on the choices of which edges are joined and which are separated. The edges that are cut from a convex polyhedron to form a net must form a spanning tree of t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descriptive Geometry
Descriptive geometry is the branch of geometry which allows the representation of three-dimensional objects in two dimensions by using a specific set of procedures. The resulting techniques are important for engineering, architecture, design and in art. The theoretical basis for descriptive geometry is provided by planar geometric projections. The earliest known publication on the technique was "Underweysung der Messung mit dem Zirckel und Richtscheyt", published in Linien, Nuremberg: 1525, by Albrecht Dürer. Italian architect Guarino Guarini was also a pioneer of projective and descriptive geometry, as is clear from his ''Placita Philosophica'' (1665), ''Euclides Adauctus'' (1671) and ''Architettura Civile'' (1686—not published until 1737), anticipating the work of Gaspard Monge (1746–1818), who is usually credited with the invention of descriptive geometry. Gaspard Monge is usually considered the "father of descriptive geometry" due to his developments in geometric pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |


.png)