|
Descriptive Geometry
Descriptive geometry is the branch of geometry which allows the representation of three-dimensional objects in two dimensions by using a specific set of procedures. The resulting techniques are important for engineering, architecture, design and in art. The theoretical basis for descriptive geometry is provided by graphical projection, planar geometric projections. The earliest known publication on the technique was "Underweysung der Messung mit dem Zirckel und Richtscheyt" (''Observation of the measurement with the compass and spirit level''), published in Linien, Nuremberg: 1525, by Albrecht Dürer. Italian architect Guarino Guarini was also a pioneer of projective and descriptive geometry, as is clear from his ''Placita Philosophica'' (1665), ''Euclides Adauctus'' (1671) and ''Architettura Civile'' (1686—not published until 1737), anticipating the work of Gaspard Monge (1746–1818), who is usually credited with the invention of descriptive geometry. Gaspard Monge is usu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ACM Computing Surveys
''ACM Computing Surveys'' is peer-reviewed quarterly scientific journal and is published by the Association for Computing Machinery. It publishes survey articles and tutorials related to computer science and computing. The journal was established in 1969 with William S. Dorn as founding editor-in-chief. According to the ''Journal Citation Reports'', the journal has a 2023 impact factor The impact factor (IF) or journal impact factor (JIF) of an academic journal is a type of journal ranking. Journals with higher impact factor values are considered more prestigious or important within their field. The Impact Factor of a journa ... of 23.8. In a 2008 ranking of computer science journals, ''ACM Computing Surveys'' received the highest rank "A*". See also *'' ACM Computing Reviews'' References External links * Computer science journals Information systems journals Computing Surveys Academic journals established in 1969 Review journals {{compu-journal-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
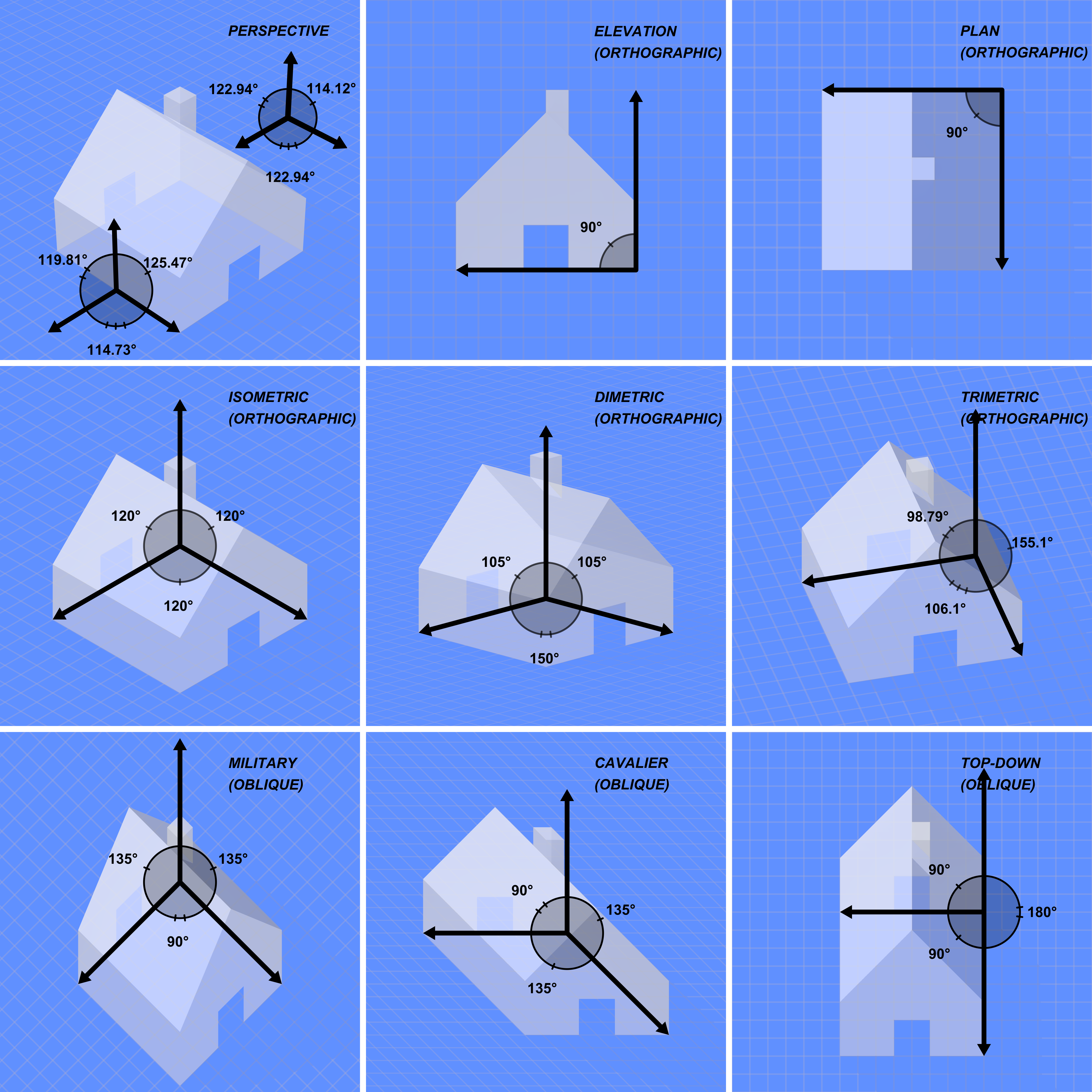
Trimetric Projection
Axonometric projection is a type of orthographic projection used for creating a pictorial drawing of an object, where the object is rotated around one or more of its axes to reveal multiple sides.Gary R. Bertoline et al. (2002) ''Technical Graphics Communication''. McGraw–Hill Professional, 2002. , p. 330. Overview "Axonometry" means "to measure along the axes". In German literature, axonometry is based on Pohlke's theorem, such that the scope of axonometric projection could encompass ''every'' type of parallel projection, including not only orthographic projection (and multiview projection), but also oblique projection. However, outside of German literature, the term "axonometric" is sometimes used only to distinguish between orthographic views where the principal axes of an object are ''not'' orthogonal to the projection plane, and orthographic views in which the principal axes of the object ''are'' orthogonal to the projection plane. (In multiview projection thes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isometric Projection
Isometric projection is a method for visually representing three-dimensional objects in two dimensions in technical and engineering drawings. It is an axonometric projection in which the three coordinate axes appear equally foreshortened and the angle between any two of them is 120 degrees. Overview The term "isometric" comes from the Greek for "equal measure", reflecting that the scale along each axis of the projection is the same (unlike some other forms of graphical projection). An isometric view of an object can be obtained by choosing the viewing direction such that the angles between the projections of the ''x'', ''y'', and ''z'' axes are all the same, or 120°. For example, with a cube, this is done by first looking straight towards one face. Next, the cube is rotated ±45° about the vertical axis, followed by a rotation of approximately 35.264° (precisely arcsin or arctan , which is related to the Magic angle) about the horizontal axis. Note that with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Axonometric Projection
Axonometric projection is a type of orthographic projection used for creating a pictorial drawing of an object, where the object is rotated around one or more of its axes to reveal multiple sides.Gary R. Bertoline et al. (2002) ''Technical Graphics Communication''. McGraw–Hill Professional, 2002. , p. 330. Overview "Axonometry" means "to measure along the axes". In German literature, axonometry is based on Pohlke's theorem, such that the scope of axonometric projection could encompass ''every'' type of parallel projection, including not only orthographic projection (and multiview projection), but also oblique projection. However, outside of German literature, the term "axonometric" is sometimes used only to distinguish between orthographic views where the principal axes of an object are ''not'' orthogonal to the projection plane, and orthographic views in which the principal axes of the object ''are'' orthogonal to the projection plane. (In multiview projection thes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Orthographic Projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in which all the projection lines are orthogonal to the projection plane, resulting in every plane of the scene appearing in affine transformation on the viewing surface. The obverse of an orthographic projection is an oblique projection, which is a parallel projection in which the projection lines are ''not'' orthogonal to the projection plane. The term ''orthographic'' sometimes means a technique in multiview projection in which principal axes or the planes of the subject are also parallel with the projection plane to create the ''primary views''. If the principal planes or axes of an object in an orthographic projection are ''not'' parallel with the projection plane, the depiction is called ''axonometric'' or an ''auxiliary views''. (''Ax ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Graphical Projection
A 3D projection (or graphical projection) is a design technique used to display a three-dimensional (3D) object on a two-dimensional (2D) surface. These projections rely on visual perspective and aspect analysis to project a complex object for viewing capability on a simpler plane. 3D projections use the primary qualities of an object's basic shape to create a map of points, that are then connected to one another to create a visual element. The result is a graphic that contains conceptual properties to interpret the figure or image as not actually flat (2D), but rather, as a solid object (3D) being viewed on a 2D display. 3D objects are largely displayed on two-dimensional mediums (such as paper and computer monitors). As such, graphical projections are a commonly used design element; notably, in engineering drawing, drafting, and computer graphics. Projections can be calculated through employment of mathematical analysis and formulae, or by using various geometric and op ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Projective Geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''projective space'') and a selective set of basic geometric concepts. The basic intuitions are that projective space has more points than Euclidean space, for a given dimension, and that geometric transformations are permitted that transform the extra points (called "Point at infinity, points at infinity") to Euclidean points, and vice versa. Properties meaningful for projective geometry are respected by this new idea of transformation, which is more radical in its effects than can be expressed by a transformation matrix and translation (geometry), translations (the affine transformations). The first issue for geometers is what kind of geometry is adequate for a novel situation. Unlike in Euclidean geometry, the concept of an angle does not ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Descriptive Geometry - Skew Lines Appear In Specified Length Ratio
In the study of language, description or descriptive linguistics is the work of objectively analyzing and describing how language is actually used (or how it was used in the past) by a speech community. François & Ponsonnet (2013). All academic research in linguistics is descriptive; like all other scientific disciplines, it aims to describe reality, without the bias of preconceived ideas about how it ought to be. Modern descriptive linguistics is based on a structural approach to language, as exemplified in the work of Leonard Bloomfield and others. This type of linguistics utilizes different methods in order to describe a language such as basic data collection, and different types of elicitation methods. Descriptive versus prescriptive linguistics Linguistic description, as used in academic and professional linguistics, is often contrasted with linguistic prescription, — entry for "Descriptivism and prescriptivism" quotation: "Contrasting terms in linguistics." (p.286) ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |