Descriptive geometry on:
[Wikipedia]
[Google]
[Amazon]
 Descriptive geometry is the branch of
Descriptive geometry is the branch of
 Given the X, Y and Z coordinates of P, R, S and U, projections 1 and 2 are drawn to scale on the X-Y and X-Z planes, respectively. Projections 1 and 2 are delineated by hinge line H1,2, and aligned such that each point projects perpendicularly across the hinge line (P1:P2, R1:R2, S1:S2, U1:U2).
To get a true view (length in the projection is equal to length in 3D space) of one of the lines: SU in this example, the projection 3 view is chosen perpendicular to S2U2 by drawing a hinge line H2,3 parallel to S2U2. To get an end view of SU, the projection 4 view is chosen is perpendicular to the true view of line S3U3 by drawing a hinge line H3,4 perpendicular to S3U3. The perpendicular QT is the true length of the connector and its distance ''d'' gives the shortest distance between PR and SU.
To locate points Q and T on these lines giving this shortest distance, projection 5 is drawn with hinge line H4,5 perpendicular to QT and parallel to P4R4, making both P5R5 and S5U5 true views (any projection of an end view is a true view). Projecting the intersection of these lines, Q5 and T5 back to projection 1 (magenta lines and labels) allows their coordinates to be read off the X, Y and Z axes.
Given the X, Y and Z coordinates of P, R, S and U, projections 1 and 2 are drawn to scale on the X-Y and X-Z planes, respectively. Projections 1 and 2 are delineated by hinge line H1,2, and aligned such that each point projects perpendicularly across the hinge line (P1:P2, R1:R2, S1:S2, U1:U2).
To get a true view (length in the projection is equal to length in 3D space) of one of the lines: SU in this example, the projection 3 view is chosen perpendicular to S2U2 by drawing a hinge line H2,3 parallel to S2U2. To get an end view of SU, the projection 4 view is chosen is perpendicular to the true view of line S3U3 by drawing a hinge line H3,4 perpendicular to S3U3. The perpendicular QT is the true length of the connector and its distance ''d'' gives the shortest distance between PR and SU.
To locate points Q and T on these lines giving this shortest distance, projection 5 is drawn with hinge line H4,5 perpendicular to QT and parallel to P4R4, making both P5R5 and S5U5 true views (any projection of an end view is a true view). Projecting the intersection of these lines, Q5 and T5 back to projection 1 (magenta lines and labels) allows their coordinates to be read off the X, Y and Z axes.

''Figure 1: Descriptive geometry - skew lines appearing perpendicular''

''Figure 2: Descriptive geometry - skew lines appear equal length''
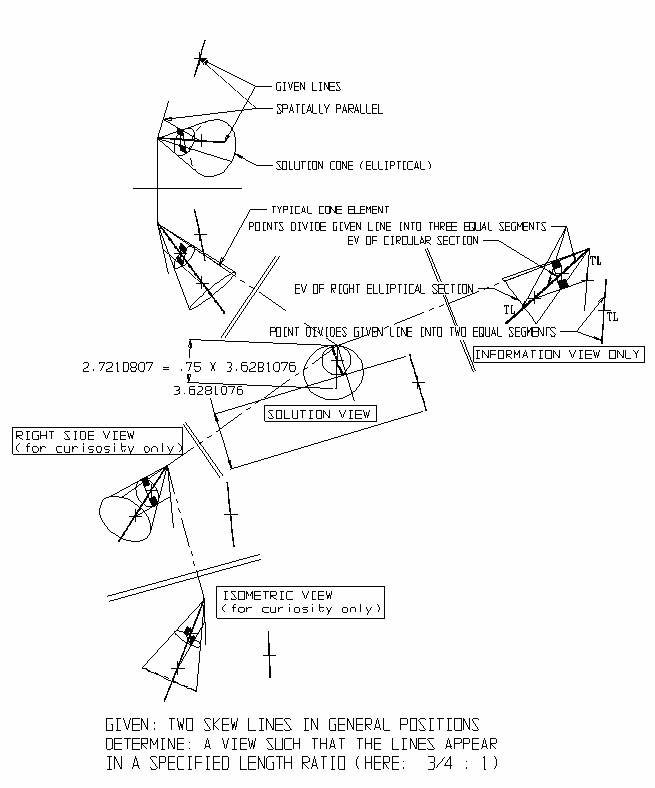
''Figure 3: Descriptive geometry - skew lines appear in specified length ratio''
geometry
Geometry (; ) is a branch of mathematics concerned with properties of space such as the distance, shape, size, and relative position of figures. Geometry is, along with arithmetic, one of the oldest branches of mathematics. A mathematician w ...
which allows the representation of three-dimensional objects in two dimensions by using a specific set of procedures. The resulting techniques are important for engineering
Engineering is the practice of using natural science, mathematics, and the engineering design process to Problem solving#Engineering, solve problems within technology, increase efficiency and productivity, and improve Systems engineering, s ...
, architecture
Architecture is the art and technique of designing and building, as distinguished from the skills associated with construction. It is both the process and the product of sketching, conceiving, planning, designing, and construction, constructi ...
, design
A design is the concept or proposal for an object, process, or system. The word ''design'' refers to something that is or has been intentionally created by a thinking agent, and is sometimes used to refer to the inherent nature of something ...
and in art. The theoretical basis for descriptive geometry is provided by planar geometric projections. The earliest known publication on the technique was "Underweysung der Messung mit dem Zirckel und Richtscheyt" (''Observation of the measurement with the compass and spirit level''), published in Linien, Nuremberg: 1525, by Albrecht Dürer
Albrecht Dürer ( , ;; 21 May 1471 – 6 April 1528),Müller, Peter O. (1993) ''Substantiv-Derivation in Den Schriften Albrecht Dürers'', Walter de Gruyter. . sometimes spelled in English as Durer or Duerer, was a German painter, Old master prin ...
. Italian architect Guarino Guarini
Camillo Guarino Guarini (17 January 16246 March 1683) was an Italian architect of the Piedmontese Baroque architecture, Baroque, active in Turin as well as Sicily, Kingdom of France, France and Kingdom of Portugal, Portugal. He was a Theatines, ...
was also a pioneer of projective and descriptive geometry, as is clear from his ''Placita Philosophica'' (1665), ''Euclides Adauctus'' (1671) and ''Architettura Civile'' (1686—not published until 1737), anticipating the work of Gaspard Monge
Gaspard Monge, Comte de Péluse (; 9 May 1746 – 28 July 1818) was a French mathematician, commonly presented as the inventor of descriptive geometry, (the mathematical basis of) technical drawing, and the father of differential geometry. Dur ...
(1746–1818), who is usually credited with the invention of descriptive geometry. Gaspard Monge is usually considered the "father of descriptive geometry" due to his developments in geometric problem solving. His first discoveries were in 1765 while he was working as a draftsman for military fortifications, although his findings were published later on.
Monge's protocols allow an imaginary object to be drawn in such a way that it may be modeled in three dimensions. All geometric aspects of the imaginary object are accounted for in true size/to-scale and shape, and can be imaged as seen from any position in space. All images are represented on a two-dimensional surface.
Descriptive geometry uses the image-creating technique of imaginary, parallel projectors emanating from an imaginary object and intersecting an imaginary plane of projection at right angles. The cumulative points of intersections create the desired image.
Protocols
*Project two images of an object into mutually perpendicular, arbitrary directions. Each image view accommodates three dimensions of space, two dimensions displayed as full-scale, mutually-perpendicular axes and one as an invisible (point view) axis receding into the image space (depth). Each of the two adjacent image views shares a full-scale view of one of the three dimensions of space. * Either of these images may serve as the beginning point for a third projected view. The third view may begin a fourth projection, and on ad infinitum. These sequential projections each represent a circuitous, 90° turn in space in order to view the object from a different direction. * Each new projection utilizes a dimension in full scale that appears as point-view dimension in the previous view. To achieve the full-scale view of this dimension and accommodate it within the new view requires one to ignore the previous view and proceed to the second previous view where this dimension appears in full-scale. * Each new view may be created by projecting into any of an infinite number of directions, perpendicular to the previous direction of projection. (Envision the many directions of the spokes of a wagon wheel each perpendicular to the direction of the axle.) The result is one of stepping circuitously about an object in 90° turns and viewing the object from each step. Each new view is added as an additional view to anorthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in ...
layout display and appears in an "unfolding of the glass box model".
Aside from the orthographic, six standard principal views (front; right side; left side; top; bottom; rear), descriptive geometry strives to yield four basic solution views: the true length of a line (i.e., full size, not foreshortened), the point view (end view) of a line, the true shape of a plane (i.e., full size to scale, or not foreshortened), and the edge view of a plane (i.e., view of a plane with the line of sight perpendicular to the line of sight associated with the line of sight for producing the true shape of a plane). These often serve to determine the direction of projection for the subsequent view. By the 90° circuitous stepping process, projecting in any direction from the point view of a line yields its true length view; projecting in a direction parallel to a true length line view yields its point view, projecting the point view of any line on a plane yields the plane's edge view; projecting in a direction perpendicular to the edge view of a plane will yield the true shape (to scale) view. These various views may be called upon to help solve engineering problems posed by solid-geometry principles
Heuristics
There is heuristic value to studying descriptive geometry. It promotes visualization and spatial analytical abilities, as well as the intuitive ability to recognize the direction of viewing for best presenting a geometric problem for solution. Representative examples:The best direction to view
* Twoskew lines
In three-dimensional geometry, skew lines are two Line (geometry), lines that do not Line-line intersection, intersect and are not Parallel (geometry), parallel. A simple example of a pair of skew lines is the pair of lines through opposite edges ...
(pipes, perhaps) in general positions in order to determine the location of their shortest connector (common perpendicular)
* Two skew lines (pipes) in general positions such that their shortest connector is seen in full scale
* Two skew lines in general positions such the shortest connector parallel to a given plane is seen in full scale (say, to determine the position and the dimension of the shortest connector at a constant distance from a radiating surface)
* A plane surface such that a hole drilled perpendicular is seen in full scale, as if looking through the hole (say, to test for clearances with other drilled holes)
* A plane equidistant from two skew lines in general positions (say, to confirm safe radiation distance?)
* The shortest distance from a point to a plane (say, to locate the most economical position for bracing)
* The line of intersection between two surfaces, including curved surfaces (say, for the most economical sizing of sections?)
* The true size of the angle between two planes
A standard for presenting computer-modeling views analogous to orthographic, sequential projections has not yet been adopted. One candidate for such is presented in the illustrations below. The images in the illustrations were created using three-dimensional, engineering computer graphics.
Three-dimensional computer modeling produces virtual space ''behind the screen'' and may produce any view of a model from any direction within this virtual space. It does so without the need for adjacent orthographic views and therefore may seem to render the circuitous, stepping protocol of descriptive geometry obsolete. However, since descriptive geometry is the science of the legitimate or allowable imaging of three or ''more'' dimensional space, on a flat plane, it is an indispensable study, to enhance computer modeling possibilities.
Examples
Finding the shortest connector line QT between two given skew lines PR and SU
General solutions
General solutions are a class of solutions within descriptive geometry that contain all possible solutions to a problem. The general solution is represented by a single, three-dimensional object, usually a cone, the directions of the elements of which are the desired direction of viewing (projection) for any of an infinite number of solution views. For example: To find the general solution such that two, unequal length, skew lines in general positions (say, rockets in flight?) appear: * Equal length * Equal length and parallel * Equal length and perpendicular (say, for ideal targeting of at least one) * Equal to lengths of a specified ratio * others. In the examples, the general solution for each desired characteristic solution is a cone, each element of which produces one of an infinite number of solution views. When two or more characteristics of, say those listed above, are desired (and for which a solution exists) projecting in the direction of either of the two elements of intersections (one element, if cones are tangent) between the two cones produces the desired solution view. If the cones do not intersect a solution does not exist. The examples below are annotated to show the descriptive geometric principles used in the solutions. TL = True-Length; EV = Edge View. Figs. 1-3 below demonstrate (1) Descriptive geometry, general solutions and (2) simultaneously, a potential standard for presenting such solutions in orthographic, multiview, layout formats. The potential standard employs two adjacent, standard, orthographic views (here, Front and Top) with a standard "folding line" between. As there is no subsequent need to 'circuitously step' 90° around the object, in standard, two-step sequences in order to arrive at a solution view (it is possible to go directly to the solution view), this shorter protocol is accounted for in the layout. Where the one step protocol replaces the two-step protocol, "double folding" lines are used. In other words, when one crosses the double lines he is not making a circuitous 90° turn but a non-orthodirectional turn directly to the solution view. As most engineering computer graphics packages automatically generates the six principal views of the glass box model, as well as an isometric view, these views are sometimes added out of heuristic curiosity.
''Figure 1: Descriptive geometry - skew lines appearing perpendicular''

''Figure 2: Descriptive geometry - skew lines appear equal length''

''Figure 3: Descriptive geometry - skew lines appear in specified length ratio''
See also
*Projective geometry
In mathematics, projective geometry is the study of geometric properties that are invariant with respect to projective transformations. This means that, compared to elementary Euclidean geometry, projective geometry has a different setting (''p ...
* Graphical projection
**Orthographic projection
Orthographic projection (also orthogonal projection and analemma) is a means of representing Three-dimensional space, three-dimensional objects in Plane (mathematics), two dimensions. Orthographic projection is a form of parallel projection in ...
** Axonometric projection
***Isometric projection
Isometric projection is a method for visually representing three-dimensional objects in two dimensions in technical and engineering drawings. It is an axonometric projection in which the three coordinate axes appear equally foreshortened and ...
*** Dimetric projection
*** Trimetric projection
** Orthogonal projection
** Oblique projection
** Perspective projection, Perspective (graphical)
Linear or point-projection perspective () is one of two types of graphical projection perspective in the graphic arts; the other is parallel projection. Linear perspective is an approximate representation, generally on a flat surface, of ...
* Stereotomy (descriptive geometry)
*Technical drawing
Technical drawing, drafting or drawing, is the act and discipline of composing drawings that visually communicate how something functions or is constructed.
Technical drawing is essential for communicating ideas in industry and engineering. ...
*Engineering drawing
An engineering drawing is a type of technical drawing that is used to convey information about an object. A common use is to specify the geometry necessary for the construction of a component and is called a detail drawing. Usually, a number of ...
References
Sources
* {{Authority control