|
Triplet State
In quantum mechanics, a triplet is a quantum state of a system with a spin of quantum number =1, such that there are three allowed values of the spin component, = −1, 0, and +1. Spin, in the context of quantum mechanics, is not a mechanical rotation but a more abstract concept that characterizes a particle's intrinsic angular momentum. It is particularly important for systems at atomic length scales, such as individual atoms, protons, or electrons. Almost all molecules encountered in daily life exist in a singlet state, but molecular oxygen is an exception. At room temperature, O2 exists in a triplet state, which can only undergo a chemical reaction by making the forbidden transition into a singlet state. This makes it kinetically nonreactive despite being thermodynamically one of the strongest oxidants. Photochemical or thermal activation can bring it into the singlet state, which makes it kinetically as well as thermodynamically a very strong oxidant. __TOC__ Two spin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Multiplicity Diagram
Spin or spinning most often refers to: * Spinning (textiles), the creation of yarn or thread by twisting fibers together, traditionally by hand spinning * Spin, the rotation of an object around a central axis * Spin (propaganda), an intentionally biased portrayal of something Spin, spinning or spinnin may also refer to: Physics and mathematics * Spin, the rotation of an object around a central axis * Spin (physics) or particle spin, a fundamental property of elementary particles * Spin group, a particular double cover of the special orthogonal group SO(''n'') * Spin tensor, a tensor quantity for describing spinning motion in special relativity and general relativity * Spin (aerodynamics), autorotation of an aerodynamically stalled aeroplane * SPIN bibliographic database, an indexing and abstracting service focusing on physics research Textile arts * Spinning (polymers), a process for creating polymer fibres * Spinning (textiles), the creation of yarn or thread by twisting fib ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Singlet State
In quantum mechanics, a singlet state usually refers to a system in which all electrons are paired. The term 'singlet' originally meant a linked set of particles whose net angular momentum is zero, that is, whose overall spin quantum number s=0. As a result, there is only one spectral line of a singlet state. In contrast, a doublet state contains one unpaired electron and shows splitting of spectral lines into a doublet; and a triplet state has two unpaired electrons and shows threefold splitting of spectral lines. History Singlets and the related spin concepts of doublets and triplets occur frequently in atomic physics and nuclear physics, where one often needs to determine the total spin of a collection of particles. Since the only observed fundamental particle with zero spin is the extremely inaccessible Higgs boson, singlets in everyday physics are necessarily composed of sets of particles whose individual spins are non-zero, e.g. or 1. The origin of the term "singlet" ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Mechanics
Quantum mechanics is a fundamental theory in physics that provides a description of the physical properties of nature at the scale of atoms and subatomic particles. It is the foundation of all quantum physics including quantum chemistry, quantum field theory, quantum technology, and quantum information science. Classical physics, the collection of theories that existed before the advent of quantum mechanics, describes many aspects of nature at an ordinary ( macroscopic) scale, but is not sufficient for describing them at small (atomic and subatomic) scales. Most theories in classical physics can be derived from quantum mechanics as an approximation valid at large (macroscopic) scale. Quantum mechanics differs from classical physics in that energy, momentum, angular momentum, and other quantities of a bound system are restricted to discrete values ( quantization); objects have characteristics of both particles and waves (wave–particle duality); and there are limit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Prentice Hall
Prentice Hall was an American major educational publisher owned by Savvas Learning Company. Prentice Hall publishes print and digital content for the 6–12 and higher-education market, and distributes its technical titles through the Safari Books Online e-reference service. History On October 13, 1913, law professor Charles Gerstenberg and his student Richard Ettinger founded Prentice Hall. Gerstenberg and Ettinger took their mothers' maiden names, Prentice and Hall, to name their new company. Prentice Hall became known as a publisher of trade books by authors such as Norman Vincent Peale; elementary, secondary, and college textbooks; loose-leaf information services; and professional books. Prentice Hall acquired the training provider Deltak in 1979. Prentice Hall was acquired by Gulf+Western in 1984, and became part of that company's publishing division Simon & Schuster. S&S sold several Prentice Hall subsidiaries: Deltak and Resource Systems were sold to National Education ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
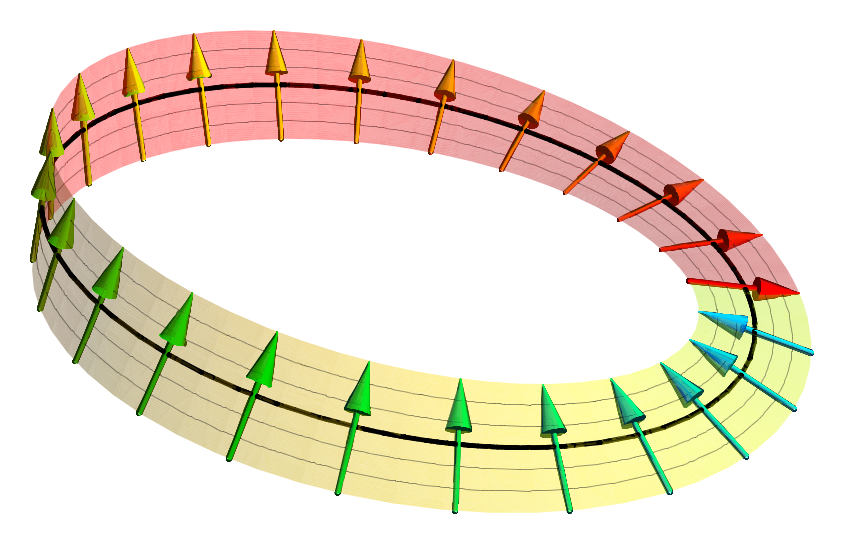
Spinor
In geometry and physics, spinors are elements of a complex vector space that can be associated with Euclidean space. Like geometric vectors and more general tensors, spinors transform linearly when the Euclidean space is subjected to a slight ( infinitesimal) rotation. Unlike vectors and tensors, a spinor transforms to its negative when the space is continuously rotated through a complete turn from 0° to 360° (see picture). This property characterizes spinors: spinors can be viewed as the "square roots" of vectors (although this is inaccurate and may be misleading; they are better viewed as "square roots" of sections of vector bundles – in the case of the exterior algebra bundle of the cotangent bundle, they thus become "square roots" of differential forms). It is also possible to associate a substantially similar notion of spinor to Minkowski space, in which case the Lorentz transformations of special relativity play the role of rotations. Spinors were introduced in ge ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Tensor
In mathematics, mathematical physics, and theoretical physics, the spin tensor is a quantity used to describe the rotational motion of particles in spacetime. The tensor has application in general relativity and special relativity, as well as quantum mechanics, relativistic quantum mechanics, and quantum field theory. The special Euclidean group SE(''d'') of direct isometries is generated by translations and rotations. Its Lie algebra is written \mathfrak(d). This article uses Cartesian coordinates and tensor index notation. Background on Noether currents The Noether current for translations in space is momentum, while the current for increments in time is energy. These two statements combine into one in spacetime: translations in spacetime, i.e. a displacement between two events, is generated by the four-momentum ''P''. Conservation of four-momentum is given by the continuity equation: :\partial_\nu T^ = 0\,, where T^ \, is the stress–energy tensor, and ∂ are partial ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin-1/2
In quantum mechanics, spin is an intrinsic property of all elementary particles. All known fermions, the particles that constitute ordinary matter, have a spin of . The spin number describes how many symmetrical facets a particle has in one full rotation; a spin of means that the particle must be rotated by two full turns (through 720°) before it has the same configuration as when it started. Particles having net spin include the proton, neutron, electron, neutrino, and quarks. The dynamics of spin- objects cannot be accurately described using classical physics; they are among the simplest systems which require quantum mechanics to describe them. As such, the study of the behavior of spin- systems forms a central part of quantum mechanics. Stern–Gerlach experiment The necessity of introducing half-integer spin goes back experimentally to the results of the Stern–Gerlach experiment. A beam of atoms is run through a strong heterogeneous magnetic field, which then ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Quantum Number
In atomic physics, the spin quantum number is a quantum number (designated ) which describes the intrinsic angular momentum (or spin angular momentum, or simply spin) of an electron or other particle. The phrase was originally used to describe the fourth of a set of quantum numbers (the principal quantum number , the azimuthal quantum number , the magnetic quantum number , and the spin quantum number ), which completely describe the quantum state of an electron in an atom. The name comes from a physical spinning of the electron about an axis, as proposed by Uhlenbeck and Goudsmit. The value of is the component of spin angular momentum parallel to a given direction (the –axis), which can be either +1/2 or –1/2 (in units of the reduced Planck constant). However this simplistic picture was quickly realized to be physically impossible because it would require the electrons to rotate faster than the speed of light. It was therefore replaced by a more abstract quantum-me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Spin Multiplicity
Spin is a conserved quantity carried by elementary particles, and thus by composite particles (hadrons) and atomic nuclei. Spin is one of two types of angular momentum in quantum mechanics, the other being ''orbital angular momentum''. The orbital angular momentum operator is the quantum-mechanical counterpart to the classical angular momentum of orbital revolution and appears when there is periodic structure to its wavefunction as the angle varies. For photons, spin is the quantum-mechanical counterpart of the polarization of light; for electrons, the spin has no classical counterpart. The existence of electron spin angular momentum is inferred from experiments, such as the Stern–Gerlach experiment, in which silver atoms were observed to possess two possible discrete angular momenta despite having no orbital angular momentum. The existence of the electron spin can also be inferred theoretically from the spin–statistics theorem and from the Pauli exclusion principle—and v ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pauli Matrices
In mathematical physics and mathematics, the Pauli matrices are a set of three complex matrices which are Hermitian, involutory and unitary. Usually indicated by the Greek letter sigma (), they are occasionally denoted by tau () when used in connection with isospin symmetries. \begin \sigma_1 = \sigma_\mathrm &= \begin 0&1\\ 1&0 \end \\ \sigma_2 = \sigma_\mathrm &= \begin 0& -i \\ i&0 \end \\ \sigma_3 = \sigma_\mathrm &= \begin 1&0\\ 0&-1 \end \\ \end These matrices are named after the physicist Wolfgang Pauli. In quantum mechanics, they occur in the Pauli equation which takes into account the interaction of the spin of a particle with an external electromagnetic field. They also represent the interaction states of two polarization filters for horizontal/vertical polarization, 45 degree polarization (right/left), and circular polarization (right/left). Each Pauli matrix is Hermitian, and together with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Angular Momentum
In physics, angular momentum (rarely, moment of momentum or rotational momentum) is the rotational analog of linear momentum. It is an important physical quantity because it is a conserved quantity—the total angular momentum of a closed system remains constant. Angular momentum has both a direction and a magnitude, and both are conserved. Bicycles and motorcycles, frisbees, rifled bullets, and gyroscopes owe their useful properties to conservation of angular momentum. Conservation of angular momentum is also why hurricanes form spirals and neutron stars have high rotational rates. In general, conservation limits the possible motion of a system, but it does not uniquely determine it. The three-dimensional angular momentum for a point particle is classically represented as a pseudovector , the cross product of the particle's position vector (relative to some origin) and its momentum vector; the latter is in Newtonian mechanics. Unlike linear momentum, angular mome ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diradical
In chemistry, a diradical is a molecular species with two electrons occupying molecular orbitals (MOs) which are degenerate. The term "diradical" is mainly used to describe organic compounds, where most diradicals are extremely reactive and in fact rarely isolated. Diradicals are even-electron molecules but have one fewer bond than the number permitted by the octet rule. Examples of diradical species can also be found in coordination chemistry, for example among bis(1,2-dithiolene) metal complexes. Spin states Diradicals are usually triplets. The phrases ''singlet'' and ''triplet'' are derived from the multiplicity of states of diradicals in electron spin resonance: a singlet diradical has one state (S = 0, Ms = 2*0+1 = 1, ms = 0) and exhibits no signal in EPR and a triplet diradical has 3 states (S = 1, Ms = 2*1+1 = 3, ms = -1; 0; 1) and shows in EPR 2 peaks (if no hyperfine splitting). The triplet state has total spin quantum number S = 1 and is paramagnetic. Therefore ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |

.gif)


