|
Time-invariant
In control theory, a time-invariant (TI) system has a time-dependent system function that is not a direct function of time. Such systems are regarded as a class of systems in the field of system analysis. The time-dependent system function is a function of the time-dependent input function. If this function depends ''only'' indirectly on the time-domain (via the input function, for example), then that is a system that would be considered time-invariant. Conversely, any direct dependence on the time-domain of the system function could be considered as a "time-varying system". Mathematically speaking, "time-invariance" of a system is the following property: :''Given a system with a time-dependent output function , and a time-dependent input function , the system will be considered time-invariant if a time-delay on the input directly equates to a time-delay of the output function. For example, if time is "elapsed time", then "time-invariance" implies that the relationship betw ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
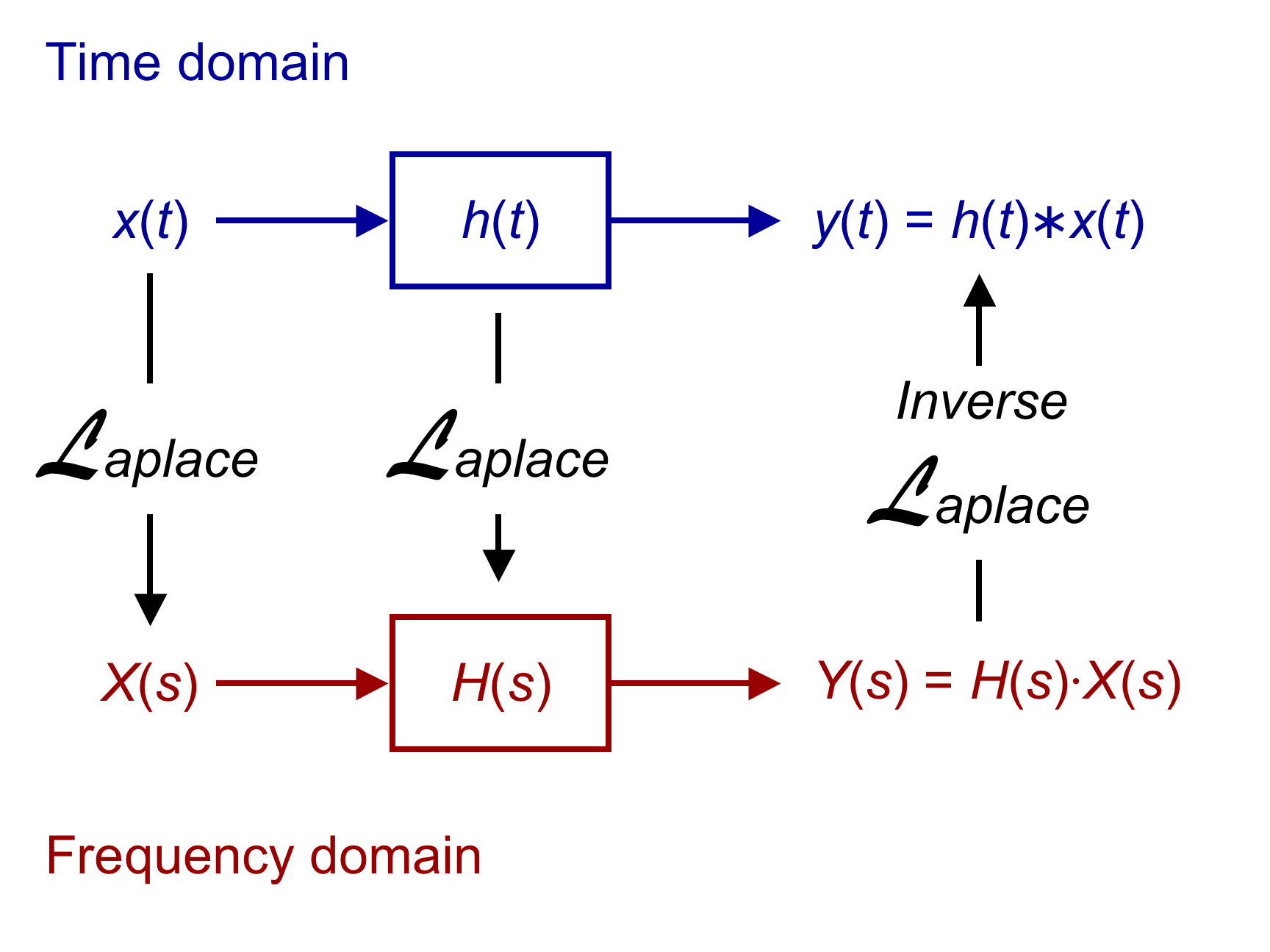
LTI System Theory
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined in the overview below. These properties apply (exactly or approximately) to many important physical systems, in which case the response of the system to an arbitrary input can be found directly using convolution: where is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication). What's more, there are systematic methods for solving any such system (determining ), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers. Linear time-invariant system theory is also used in image processing, where the s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
State Space (controls)
In control engineering and system identification, a state-space representation is a mathematical model of a physical system that uses state variables to track how inputs shape system behavior over time through first-order differential equations or difference equations. These state variables change based on their current values and inputs, while outputs depend on the states and sometimes the inputs too. The state space (also called time-domain approach and equivalent to phase space in certain dynamical systems) is a geometric space where the axes are these state variables, and the system’s state is represented by a state vector. For linear, time-invariant, and finite-dimensional systems, the equations can be written in matrix form, offering a compact alternative to the frequency domain’s Laplace transforms for multiple-input and multiple-output (MIMO) systems. Unlike the frequency domain approach, it works for systems beyond just linear ones with zero initial condi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Linear Time-invariant Theory
In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces an output signal from any input signal subject to the constraints of linearity and time-invariance; these terms are briefly defined in the overview below. These properties apply (exactly or approximately) to many important physical systems, in which case the response of the system to an arbitrary input can be found directly using convolution: where is called the system's impulse response and ∗ represents convolution (not to be confused with multiplication). What's more, there are systematic methods for solving any such system (determining ), whereas systems not meeting both properties are generally more difficult (or impossible) to solve analytically. A good example of an LTI system is any electrical circuit consisting of resistors, capacitors, inductors and linear amplifiers. Linear time-invariant system theory is also used in image processing, where the system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time-variant System
A time-variant system is a system whose output response depends on moment of observation as well as moment of input signal application. In other words, a time delay or time advance of input not only shifts the output signal in time but also changes other parameters and behavior. Time variant systems respond differently to the same input at different times. The opposite is true for time invariant systems (TIV). Overview There are many well developed techniques for dealing with the response of linear time invariant systems, such as Laplace and Fourier transforms. However, these techniques are not strictly valid for time-varying systems. A system undergoing slow time variation in comparison to its time constants can usually be considered to be time invariant: they are close to time invariant on a small scale. An example of this is the aging and wear of electronic components, which happens on a scale of years, and thus does not result in any behaviour qualitatively different from ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Time Invariance Block Diagram For A SISO System
Time is the continuous progression of existence that occurs in an apparently irreversible process, irreversible succession from the past, through the present, and into the future. It is a component quantity of various measurements used to sequence events, to compare the duration of events (or the intervals between them), and to quantify rates of change of quantities in material reality or in the qualia, conscious experience. Time is often referred to as a fourth dimension, along with Three-dimensional space, three spatial dimensions. Time is one of the seven fundamental physical quantities in both the International System of Units (SI) and International System of Quantities. The SI base unit of time is the second, which is defined by measuring the electronic transition frequency of caesium atoms. General relativity is the primary framework for understanding how spacetime works. Through advances in both theoretical and experimental investigations of spacetime, it has been shown ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Shift-invariant System
In signal processing, a shift invariant system is the discrete equivalent of a time-invariant system, defined such that if y(n) is the response of the system to x(n), then y(n-k) is the response of the system to x(n-k).Oppenheim, Schafer, 12 That is, in a shift-invariant system, the contemporaneous response of the output variable to a given value of the input variable does not depend on when the input occurs; time shifts are irrelevant in this regard. Applications Because digital systems need not be causal, some operations can be implemented in the digital domain that cannot be implemented using discrete analog components. Digital filters that require finite numbers of future values can be implemented while the analog counterparts cannot. Notes References * Oppenheim, Schafer, ''Digital Signal Processing'', Prentice Hall, 1975, See also * LTI system theory In system analysis, among other fields of study, a linear time-invariant (LTI) system is a system that produces a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Autonomous System (mathematics)
In mathematics, an autonomous system or autonomous differential equation is a simultaneous equations, system of ordinary differential equations which does not explicitly depend on the independent variable. When the variable is time, they are also called time-invariant systems. Many laws in physics, where the independent variable is usually assumed to be time, are expressed as autonomous systems because it is assumed the Physical law, laws of nature which hold now are identical to those for any point in the past or future. Definition An autonomous system is a system of ordinary differential equations of the form \fracx(t)=f(x(t)) where takes values in -dimensional Euclidean space; is often interpreted as time. It is distinguished from systems of differential equations of the form \fracx(t)=g(x(t),t) in which the law governing the evolution of the system does not depend solely on the system's current state but also the parameter , again often interpreted as time; such system ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Signal-flow Graph
A signal-flow graph or signal-flowgraph (SFG), invented by Claude Shannon, but often called a Mason graph after Samuel Jefferson Mason who coined the term, is a specialized Flow graph (mathematics), flow graph, a directed graph in which nodes represent system variables, and branches (edges, arcs, or arrows) represent functional connections between pairs of nodes. Thus, signal-flow graph theory builds on that of directed graphs (also called Digraph (mathematics), digraphs), which includes as well that of Orientation (graph theory)#Oriented graphs, oriented graphs. This mathematical theory of digraphs exists, of course, quite apart from its applications. i SFGs are most commonly used to represent signal flow in a physical systems, physical system and its controller(s), forming a cyber-physical system. Among their other uses are the representation of signal flow in various electronic networks and amplifiers, digital filters, state-variable filters and some other types of analog f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sheffer Sequence
In mathematics, a Sheffer sequence or poweroid is a polynomial sequence, i.e., a sequence of polynomials in which the index of each polynomial equals its degree, satisfying conditions related to the umbral calculus in combinatorics. They are named for Isador M. Sheffer. Definition Fix a polynomial sequence (''p''''n''). Define a linear operator ''Q'' on polynomials in ''x'' by Qp_n(x) = np_(x)\, . This determines ''Q'' on all polynomials. The polynomial sequence ''p''''n'' is a ''Sheffer sequence'' if the linear operator ''Q'' just defined is ''shift-equivariant''; such a ''Q'' is then a delta operator. Here, we define a linear operator ''Q'' on polynomials to be ''shift-equivariant'' if, whenever ''f''(''x'') = ''g''(''x'' + ''a'') = ''T''''a'' ''g''(''x'') is a "shift" of ''g''(''x''), then (''Qf'')(''x'') = (''Qg'')(''x'' + ''a''); i.e., ''Q'' commutes with every shift operator: ''T''''a''''Q'' = ''QT''''a''. Properties The set of all Sheffer sequences is a group unde ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Finite Impulse Response
In signal processing, a finite impulse response (FIR) filter is a filter whose impulse response (or response to any finite length input) is of ''finite'' duration, because it settles to zero in finite time. This is in contrast to infinite impulse response (IIR) filters, which may have internal feedback and may continue to respond indefinitely (usually decaying). The impulse response (that is, the output in response to a Kronecker delta input) of an Nth-order discrete-time FIR filter lasts exactly N+1 samples (from first nonzero element through last nonzero element) before it then settles to zero. FIR filters can be discrete-time or continuous-time, and digital or analog. Definition For a causal discrete-time FIR filter of order ''N'', each value of the output sequence is a weighted sum of the most recent input values: :\begin y &= b_0 x + b_1 x -1+ \cdots + b_N x -N\\ &= \sum_^N b_i\cdot x -i \end where: * x /math> is the input signal, * y /math> is the outpu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Commutative Operation
In mathematics, a binary operation is commutative if changing the order of the operands does not change the result. It is a fundamental property of many binary operations, and many mathematical proofs depend on it. Perhaps most familiar as a property of arithmetic, e.g. or , the property can also be used in more advanced settings. The name is needed because there are operations, such as division and subtraction, that do not have it (for example, ); such operations are ''not'' commutative, and so are referred to as noncommutative operations. The idea that simple operations, such as the multiplication and addition of numbers, are commutative was for many centuries implicitly assumed. Thus, this property was not named until the 19th century, when new algebraic structures started to be studied. Definition A binary operation * on a set ''S'' is ''commutative'' if x * y = y * x for all x,y \in S. An operation that is not commutative is said to be ''noncommutative''. One says ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Operator (mathematics)
In mathematics, an operator is generally a Map (mathematics), mapping or function (mathematics), function that acts on elements of a space (mathematics), space to produce elements of another space (possibly and sometimes required to be the same space). There is no general definition of an ''operator'', but the term is often used in place of ''function'' when the domain of a function, domain is a set of functions or other structured objects. Also, the domain of an operator is often difficult to characterize explicitly (for example in the case of an integral operator), and may be extended so as to act on related objects (an operator that acts on functions may act also on differential equations whose solutions are functions that satisfy the equation). (see Operator (physics) for other examples) The most basic operators are linear maps, which act on vector spaces. Linear operators refer to linear maps whose domain and range are the same space, for example from \mathbb^n to \mathbb^n ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |