|
Tetrakis Triphenylphosphine Palladium
Tetrakis(triphenylphosphine)palladium(0) (sometimes called quatrotriphenylphosphine palladium) is the chemical compound d(P(C6H5)3)4 often abbreviated Pd( PPh3)4, or rarely PdP4. It is a bright yellow crystalline solid that becomes brown upon decomposition in air. Structure and properties The four phosphorus atoms are at the corners of a tetrahedron surrounding the palladium(0) center. This structure is typical for four-coordinate 18 e− complexes. The corresponding complexes Ni(PPh3)4 and Pt(PPh3)4 are also well known. Such complexes reversibly dissociate PPh3 ligands in solution, so reactions attributed to Pd(PPh3)4 often in fact arise from Pd(PPh3)3 or even Pd(PPh3)2. Preparation Tetrakis(triphenylphosphine)palladium(0) was first prepared by Lamberto Malatesta et al. in the 1950s by reduction of sodium chloropalladate with hydrazine in the presence of the phosphine. It is commercially available, but can be prepared in two steps from Pd(II) precursors: :PdCl2 + 2 PPh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tetrahedral
In geometry, a tetrahedron (plural: tetrahedra or tetrahedrons), also known as a triangular pyramid, is a polyhedron composed of four triangular faces, six straight edges, and four vertex corners. The tetrahedron is the simplest of all the ordinary convex polyhedra and the only one that has fewer than 5 faces. The tetrahedron is the three-dimensional case of the more general concept of a Euclidean simplex, and may thus also be called a 3-simplex. The tetrahedron is one kind of pyramid, which is a polyhedron with a flat polygon base and triangular faces connecting the base to a common point. In the case of a tetrahedron the base is a triangle (any of the four faces can be considered the base), so a tetrahedron is also known as a "triangular pyramid". Like all convex polyhedra, a tetrahedron can be folded from a single sheet of paper. It has two such nets. For any tetrahedron there exists a sphere (called the circumsphere) on which all four vertices lie, and another ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Ligand
In coordination chemistry, a ligand is an ion or molecule ( functional group) that binds to a central metal atom to form a coordination complex. The bonding with the metal generally involves formal donation of one or more of the ligand's electron pairs, often through Lewis bases. The nature of metal–ligand bonding can range from covalent to ionic. Furthermore, the metal–ligand bond order can range from one to three. Ligands are viewed as Lewis bases, although rare cases are known to involve Lewis acidic "ligands". Metals and metalloids are bound to ligands in almost all circumstances, although gaseous "naked" metal ions can be generated in a high vacuum. Ligands in a complex dictate the reactivity of the central atom, including ligand substitution rates, the reactivity of the ligands themselves, and redox. Ligand selection requires critical consideration in many practical areas, including bioinorganic and medicinal chemistry, homogeneous catalysis, and environm ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Suzuki Coupling
The Suzuki reaction is an organic reaction, classified as a cross-coupling reaction, where the coupling partners are a boronic acid and an organohalide and the catalyst is a palladium(0) complex. It was first published in 1979 by Akira Suzuki, and he shared the 2010 Nobel Prize in Chemistry with Richard F. Heck and Ei-ichi Negishi for their contribution to the discovery and development of palladium-catalyzed cross-couplings in organic synthesis. This reaction is also known as the Suzuki–Miyaura reaction or simply as the Suzuki coupling. It is widely used to synthesize polyolefins, styrenes, and substituted biphenyls. Several reviews have been published describing advancements and the development of the Suzuki reaction. The general scheme for the Suzuki reaction is shown below, where a carbon-carbon single bond is formed by coupling a halide (R1-X) with an organoboron species (R2-BY2) using a palladium catalyst and a base. Reaction mechanism The mechanism of the Suzuki ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Heck Reaction
The Heck reaction (also called the Mizoroki–Heck reaction) is the chemical reaction of an unsaturated halide (or triflate) with an alkene in the presence of a base and a palladium catalyst (or palladium nanomaterial-based catalyst) to form a substituted alkene. It is named after Tsutomu Mizoroki and Richard F. Heck. Heck was awarded the 2010 Nobel Prize in Chemistry, which he shared with Ei-ichi Negishi and Akira Suzuki, for the discovery and development of this reaction. This reaction was the first example of a carbon-carbon bond-forming reaction that followed a Pd(0)/Pd(II) catalytic cycle, the same catalytic cycle that is seen in other Pd(0)-catalyzed cross-coupling reactions. The Heck reaction is a way to substitute alkenes. History The original reaction by Tsutomu Mizoroki (1971) describes the coupling between iodobenzene and styrene in methanol to form stilbene at 120 °C (autoclave) with potassium acetate base and palladium chloride catalysis. This work was a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
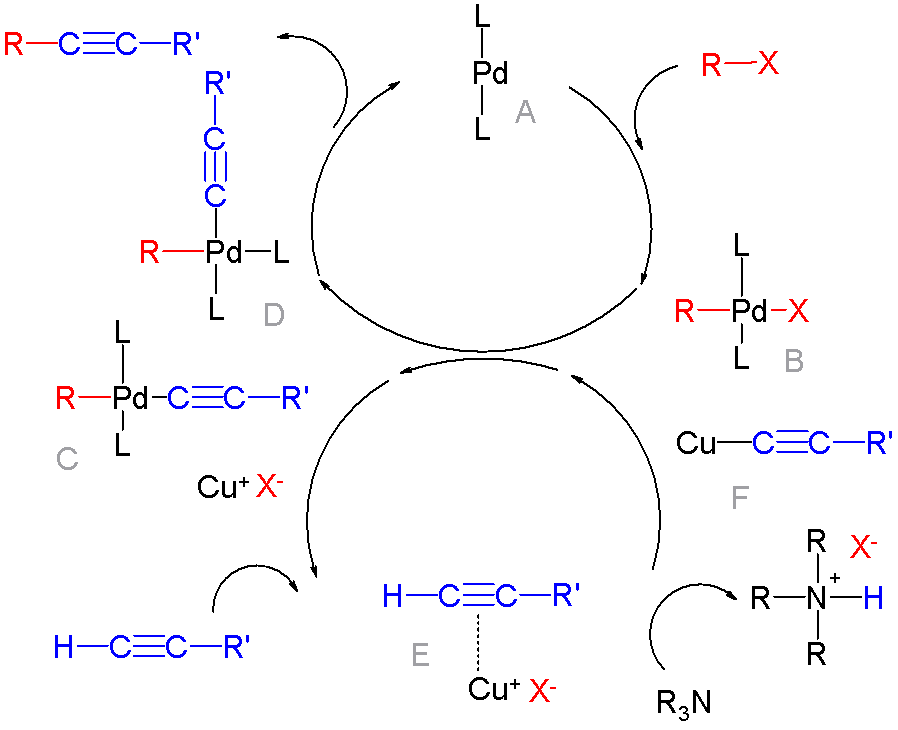
Palladium-catalyzed Coupling Reaction
In organic chemistry, a cross-coupling reaction is a reaction where two fragments are joined together with the aid of a metal catalyst. In one important reaction type, a main group organometallic compound of the type R-M (R = organic fragment, M = main group center) reacts with an organic halide of the type R'-X with formation of a new carbon–carbon bond in the product R-R'. Cross-coupling reaction are a subset of coupling reactions. It is often used in arylations. Richard F. Heck, Ei-ichi Negishi, and Akira Suzuki were awarded the 2010 Nobel Prize in Chemistry for developing palladium-catalyzed coupling reactions. Mechanism The mechanism generally involves reductive elimination of the organic substituents R and R' on a metal complex of the type LnMR(R') (where L is some arbitrary spectator ligand). The crucial intermediate LnMR(R') is formed in a two step process from a low valence precursor Ln. The oxidative addition of an organic halide (RX) to LnM gives LnMR(X). Subse ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Catalyst
Catalysis () is the process of increasing the rate of a chemical reaction by adding a substance known as a catalyst (). Catalysts are not consumed in the reaction and remain unchanged after it. If the reaction is rapid and the catalyst recycles quickly, very small amounts of catalyst often suffice; mixing, surface area, and temperature are important factors in reaction rate. Catalysts generally react with one or more reactants to form intermediates that subsequently give the final reaction product, in the process of regenerating the catalyst. Catalysis may be classified as either homogeneous, whose components are dispersed in the same phase (usually gaseous or liquid) as the reactant, or heterogeneous, whose components are not in the same phase. Enzymes and other biocatalysts are often considered as a third category. Catalysis is ubiquitous in chemical industry of all kinds. Estimates are that 90% of all commercially produced chemical products involve catalysts at some sta ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Argon
Argon is a chemical element with the symbol Ar and atomic number 18. It is in group 18 of the periodic table and is a noble gas. Argon is the third-most abundant gas in Earth's atmosphere, at 0.934% (9340 ppmv). It is more than twice as abundant as water vapor (which averages about 4000 ppmv, but varies greatly), 23 times as abundant as carbon dioxide (400 ppmv), and more than 500 times as abundant as neon (18 ppmv). Argon is the most abundant noble gas in Earth's crust, comprising 0.00015% of the crust. Nearly all of the argon in Earth's atmosphere is radiogenic argon-40, derived from the decay of potassium-40 in Earth's crust. In the universe, argon-36 is by far the most common argon isotope, as it is the most easily produced by stellar nucleosynthesis in supernovas. The name "argon" is derived from the Greek word , neuter singular form of meaning 'lazy' or 'inactive', as a reference to the fact that the element undergoes almost no chemical reactions. The comp ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Methanol
Methanol (also called methyl alcohol and wood spirit, amongst other names) is an organic chemical and the simplest aliphatic alcohol, with the formula C H3 O H (a methyl group linked to a hydroxyl group, often abbreviated as MeOH). It is a light, volatile, colourless, flammable liquid with a distinctive alcoholic odour similar to that of ethanol (potable alcohol). A polar solvent, methanol acquired the name wood alcohol because it was once produced chiefly by the destructive distillation of wood. Today, methanol is mainly produced industrially by hydrogenation of carbon monoxide. Methanol consists of a methyl group linked to a polar hydroxyl group. With more than 20 million tons produced annually, it is used as a precursor to other commodity chemicals, including formaldehyde, acetic acid, methyl tert-butyl ether, methyl benzoate, anisole, peroxyacids, as well as a host of more specialised chemicals. Occurrence Small amounts of methanol are present in normal, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Reductant
In chemistry, a reducing agent (also known as a reductant, reducer, or electron donor) is a chemical species that "donates" an electron to an (called the , , , or ). Examples of substances that are commonly reducing agents include the Earth metals, formic acid, oxalic acid, and sulfite compounds. In their pre-reaction states, reducers have extra electrons (that is, they are by themselves reduced) and oxidizers lack electrons (that is, they are by themselves oxidized). This is commonly expressed in terms of their oxidation states. An agent's oxidation state describes its degree of loss of electrons, where the higher the oxidation state then the fewer electrons it has. So initially, prior to the reaction, a reducing agent is typically in one of its lower possible oxidation states; its oxidation state increases during the reaction while that of the oxidizer decreases. Thus in a redox reaction, the agent whose oxidation state increases, that "loses/ donates electrons", that "is oxi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
One-pot Reaction
In chemistry a one-pot synthesis is a strategy to improve the efficiency of a chemical reaction whereby a reactant is subjected to successive chemical reactions in just one reactor. This is much desired by chemists because avoiding a lengthy separation process and purification of the intermediate chemical compounds can save time and resources while increasing chemical yield. An example of a one-pot synthesis is the total synthesis of tropinone or the Gassman indole synthesis. Sequential one-pot syntheses can be used to generate even complex targets with multiple stereocentres, such as oseltamivir, which may significantly shorten the number of steps required overall and have important commercial implications. A sequential one-pot synthesis with reagents added to a reactor one at a time and without work-up is also called a telescoping synthesis. In one such procedure the reaction of 3-N-tosylaminophenol I with acrolein II affords a hydroxyl substituted quinoline III through 4 se ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrazine
Hydrazine is an inorganic compound with the chemical formula . It is a simple pnictogen hydride, and is a colourless flammable liquid with an ammonia-like odour. Hydrazine is highly toxic unless handled in solution as, for example, hydrazine hydrate (). Hydrazine is mainly used as a foaming agent in preparing polymer foams, but applications also include its uses as a precursor to polymerization catalysts, pharmaceuticals, and agrochemicals, as well as a long-term storable propellant for in- space spacecraft propulsion. Additionally, hydrazine is used in various rocket fuels and to prepare the gas precursors used in air bags. Hydrazine is used within both nuclear and conventional electrical power plant steam cycles as an oxygen scavenger to control concentrations of dissolved oxygen in an effort to reduce corrosion. the world hydrazine hydrate market amounted to $350 million. About two million tons of hydrazine hydrate were used in foam blowing agents in 2015. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.jpg "Click for more on -> Tetrahedral")
4-3D-balls.png "Click for more on -> Ligand")
