|
Single-parameter Utility
In mechanism design, an agent is said to have single-parameter utility if his valuation of the possible outcomes can be represented by a single number. For example, in an auction for a single item, the utilities of all agents are single-parametric, since they can be represented by their monetary evaluation of the item. In contrast, in a combinatorial auction for two or more related items, the utilities are usually not single-parametric, since they are usually represented by their evaluations to all possible bundles of items. Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. In general, each agent can assign a different and unrelated value to every outcome in X. In the special case of single-parameter utility, each agent i has a publicly known outcome proper subset W_i \subset X which are the "winning outcomes" for agent i (e.g., in a single-item auction, W_i contains the outcome in which agent i wins the item). ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mechanism Design
Mechanism design is a field in economics and game theory that takes an objectives-first approach to designing economic mechanisms or incentives, toward desired objectives, in strategic settings, where players act rationally. Because it starts at the end of the game, then goes backwards, it is also called reverse game theory. It has broad applications, from economics and politics in such fields as market design, auction theory and social choice theory to networked-systems (internet interdomain routing, sponsored search auctions). Mechanism design studies solution concepts for a class of private-information games. Leonid Hurwicz explains that 'in a design problem, the goal function is the main "given", while the mechanism is the unknown. Therefore, the design problem is the "inverse" of traditional economic theory, which is typically devoted to the analysis of the performance of a given mechanism.' So, two distinguishing features of these games are: * that a game "designer" choos ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Auction
An auction is usually a process of buying and selling goods or services by offering them up for bids, taking bids, and then selling the item to the highest bidder or buying the item from the lowest bidder. Some exceptions to this definition exist and are described in the section about different types. The branch of economic theory dealing with auction types and participants' behavior in auctions is called auction theory. The open ascending price auction is arguably the most common form of auction and has been used throughout history. Participants bid openly against one another, with each subsequent bid being higher than the previous bid. An auctioneer may announce prices, while bidders submit bids vocally or electronically. Auctions are applied for trade in diverse contexts. These contexts include antiques, paintings, rare collectibles, expensive wines, commodities, livestock, radio spectrum, used cars, real estate, online advertising, vacation packages, emission trading, a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Combinatorial Auction
A combinatorial auction is a type of smart market in which participants can place bids on combinations of discrete heterogeneous items, or “packages”, rather than individual items or continuous quantities. These packages can be also called lots and the whole auction a multi-lot auction. Combinatorial auctions are applicable when bidders have non-additive valuations on bundles of items, that is, they value combinations of items more or less than the sum of the valuations of individual elements of the combination. Simple combinatorial auctions have been used for many years in estate auctions, where a common procedure is to accept bids for packages of items. They have been used recently for truckload transportation, bus routes, industrial procurement, and in the allocation of radio spectrum for wireless communications. In recent years, procurement teams have applied reverse combinatorial auctions in the procurement of goods and services. This application is often referred to as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Subset
In mathematics, Set (mathematics), set ''A'' is a subset of a set ''B'' if all Element (mathematics), elements of ''A'' are also elements of ''B''; ''B'' is then a superset of ''A''. It is possible for ''A'' and ''B'' to be equal; if they are unequal, then ''A'' is a proper subset of ''B''. The relationship of one set being a subset of another is called inclusion (or sometimes containment). ''A'' is a subset of ''B'' may also be expressed as ''B'' includes (or contains) ''A'' or ''A'' is included (or contained) in ''B''. A ''k''-subset is a subset with ''k'' elements. The subset relation defines a partial order on sets. In fact, the subsets of a given set form a Boolean algebra (structure), Boolean algebra under the subset relation, in which the join and meet are given by Intersection (set theory), intersection and Union (set theory), union, and the subset relation itself is the Inclusion (Boolean algebra), Boolean inclusion relation. Definition If ''A'' and ''B'' are sets and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Social Choice
Social choice theory or social choice is a theoretical framework for analysis of combining individual opinions, preferences, interests, or welfares to reach a ''collective decision'' or ''social welfare'' in some sense.Amartya Sen (2008). "Social Choice,". ''The New Palgrave Dictionary of Economics'', 2nd EditionAbstract & TOC./ref> Whereas choice theory is concerned with individuals making choices based on their preferences, social choice theory is concerned with how to translate the preferences of individuals into the preferences of a group. A non-theoretical example of a collective decision is enacting a law or set of laws under a constitution. Another example is voting, where individual preferences over candidates are collected to elect a person that best represents the group's preferences. Social choice blends elements of welfare economics and public choice theory. It is methodologically individualistic, in that it aggregates preferences and behaviors of individual member ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Monotonicity (mechanism Design)
In mechanism design, monotonicity is a property of a social choice function. It is a necessary condition for being able to implement the function using a strategyproof mechanism. Its verbal description is: In other words: Notation There is a set X of possible outcomes. There are n agents which have different valuations for each outcome. The valuation of agent i is represented as a function: v_i : X \longrightarrow R_+ which expresses the value it assigns to each alternative. The vector of all value-functions is denoted by v. For every agent i, the vector of all value-functions of the ''other'' agents is denoted by v_. So v \equiv (v_i,v_). A social choice function is a function that takes as input the value-vector v and returns an outcome x\in X. It is denoted by \text(v) or \text(v_i,v_). In mechanisms without money A social choice function satisfies the strong monotonicity property (SMON) if for every agent i and every v_i,v_i',v_, if: x = \text(v_i, v_) x' = \text ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second-price Auction
A Vickrey auction or sealed-bid second-price auction (SBSPA) is a type of sealed-bid auction. Bidders submit written bids without knowing the bid of the other people in the auction. The highest bidder wins but the price paid is the second-highest bid. This type of auction is strategically similar to an English auction and gives bidders an incentive to bid their true value. The auction was first described academically by Columbia University professor William Vickrey in 1961 though it had been used by stamp collectors since 1893. In 1797 Johann Wolfgang von Goethe sold a manuscript using a sealed-bid, second-price auction. Vickrey's original paper mainly considered auctions where only a single, indivisible good is being sold. The terms ''Vickrey auction'' and ''second-price sealed-bid auction'' are, in this case only, equivalent and used interchangeably. In the case of multiple identical goods, the bidders submit inverse demand curves and pay the opportunity cost. Vickrey auctions ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truthful Mechanism
In game theory, an asymmetric game where players have private information is said to be strategy-proof or strategyproof (SP) if it is a weakly-dominant strategy for every player to reveal his/her private information, i.e. given no information about what the others do, you fare best or at least not worse by being truthful. SP is also called truthful or dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. An SP game is not always immune to collusion, but its robust variants are; with group strategyproofness no group of people can collude to misreport their preferences in a way that makes every member better off, and with strong group strategyproofness no group of people can collude to misreport their preferences in a way that makes at least one member of the group better off without making any of the remaining members worse off. Examples Typical examples of SP mechanisms are majority voting between two alternatives, second- ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Expected Value
In probability theory, the expected value (also called expectation, expectancy, mathematical expectation, mean, average, or first moment) is a generalization of the weighted average. Informally, the expected value is the arithmetic mean of a large number of independently selected outcomes of a random variable. The expected value of a random variable with a finite number of outcomes is a weighted average of all possible outcomes. In the case of a continuum of possible outcomes, the expectation is defined by integration. In the axiomatic foundation for probability provided by measure theory, the expectation is given by Lebesgue integration. The expected value of a random variable is often denoted by , , or , with also often stylized as or \mathbb. History The idea of the expected value originated in the middle of the 17th century from the study of the so-called problem of points, which seeks to divide the stakes ''in a fair way'' between two players, who have to end th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
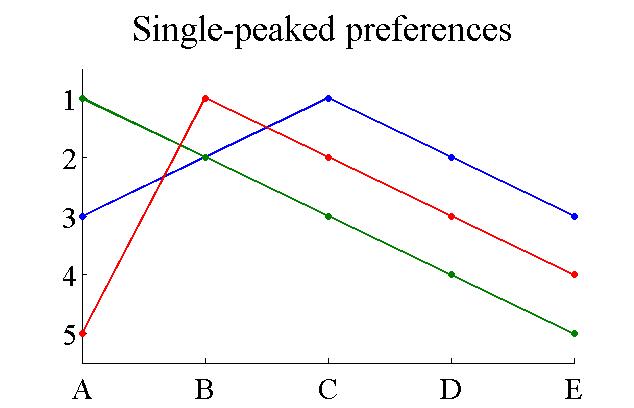
Single Peaked Preferences
Single-peaked preferences are a class of preference relations. A group of agents is said to have single-peaked preferences over a set of possible outcomes if the outcomes can be ordered along a line such that: # Each agent has a "best outcome" in the set, and - # For each agent, outcomes that are further from his or her best outcome are preferred less. Single-peaked preferences are typical of one-dimensional domains. A typical example is when several consumers have to decide on the amount of public good to purchase. The amount is a one-dimensional variable. Usually, each consumer decides on a certain quantity which is best for him or her, and if the actual quantity is more/less than that ideal quantity, the agent is then less satisfied. With single-peaked preferences, there is a simple truthful mechanism for selecting an outcome: it is to select the median quantity. See the median voter theorem. It is truthful because the median function satisfies the strong monotonicity proper ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |