|
Second Symmetric Derivative
In mathematics, the symmetric derivative is an operation generalizing the ordinary derivative. It is defined asThomson, p. 1. : \lim_ \frac. The expression under the limit is sometimes called the symmetric difference quotient. A function is said to be symmetrically differentiable at a point ''x'' if its symmetric derivative exists at that point. If a function is differentiable (in the usual sense) at a point, then it is also symmetrically differentiable, but the converse is not true. A well-known counterexample is the absolute value function , which is not differentiable at , but is symmetrically differentiable here with symmetric derivative 0. For differentiable functions, the symmetric difference quotient does provide a better numerical approximation of the derivative than the usual difference quotient. The symmetric derivative at a given point equals the arithmetic mean of the left and right derivatives at that point, if the latter two both exist. Neither Rolle's theorem nor ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Irrational Number
In mathematics, the irrational numbers (from in- prefix assimilated to ir- (negative prefix, privative) + rational) are all the real numbers that are not rational numbers. That is, irrational numbers cannot be expressed as the ratio of two integers. When the ratio of lengths of two line segments is an irrational number, the line segments are also described as being '' incommensurable'', meaning that they share no "measure" in common, that is, there is no length ("the measure"), no matter how short, that could be used to express the lengths of both of the two given segments as integer multiples of itself. Among irrational numbers are the ratio of a circle's circumference to its diameter, Euler's number ''e'', the golden ratio ''φ'', and the square root of two. In fact, all square roots of natural numbers, other than of perfect squares, are irrational. Like all real numbers, irrational numbers can be expressed in positional notation, notably as a decimal number. In the cas ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalizations Of The Derivative
In mathematics, the derivative is a fundamental construction of differential calculus and admits many possible generalizations within the fields of mathematical analysis, combinatorics, algebra, geometry, etc. Fréchet derivative The Fréchet derivative defines the derivative for general normed vector spaces V, W. Briefly, a function f : U \to W, U an open subset of V, is called ''Fréchet differentiable'' at x \in U if there exists a bounded linear operator A:V\to W such that \lim_ \frac = 0. Functions are defined as being differentiable in some open neighbourhood of x, rather than at individual points, as not doing so tends to lead to many pathological counterexamples. The Fréchet derivative is quite similar to the formula for the derivative found in elementary one-variable calculus, \lim_\frac = A, and simply moves ''A'' to the left hand side. However, the Fréchet derivative ''A'' denotes the function t \mapsto f'(x) \cdot t. In multivariable calculus, in the context ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Density Point
In mathematics, Lebesgue's density theorem states that for any Lebesgue measurable set A\subset \R^n, the "density" of ''A'' is 0 or 1 at almost every point in \R^n. Additionally, the "density" of ''A'' is 1 at almost every point in ''A''. Intuitively, this means that the "edge" of ''A'', the set of points in ''A'' whose "neighborhood" is partially in ''A'' and partially outside of ''A'', is negligible. Let μ be the Lebesgue measure on the Euclidean space R''n'' and ''A'' be a Lebesgue measurable subset of R''n''. Define the approximate density of ''A'' in a ε-neighborhood of a point ''x'' in R''n'' as : d_\varepsilon(x)=\frac where ''B''ε denotes the closed ball of radius ε centered at ''x''. Lebesgue's density theorem asserts that for almost every point ''x'' of ''A'' the density : d(x)=\lim_ d_(x) exists and is equal to 0 or 1. In other words, for every measurable set ''A'', the density of ''A'' is 0 or 1 almost everywhere in R''n''. However, if μ(''A'') >&nb ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
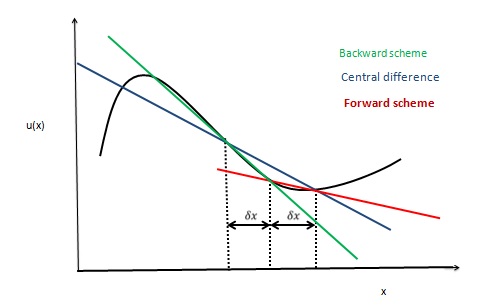
Central Differencing Scheme
In applied mathematics, the central differencing scheme is a finite difference method that optimizes the approximation for the differential operator in the central node of the considered patch and provides numerical solutions to differential equations. It is one of the schemes used to solve the integrated convection–diffusion equation and to calculate the transported property Φ at the e and w faces, where ''e'' and ''w'' are short for ''east'' and ''west'' (compass directions being customarily used to indicate directions on computational grids). The method's advantages are that it is easy to understand and implement, at least for simple material relations; and that its convergence rate is faster than some other finite differencing methods, such as forward and backward differencing. The right side of the convection-diffusion equation, which basically highlights the diffusion terms, can be represented using central difference approximation. To simplify the solution and analysis, li ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sign Function
In mathematics, the sign function or signum function (from '' signum'', Latin for "sign") is an odd mathematical function that extracts the sign of a real number. In mathematical expressions the sign function is often represented as . To avoid confusion with the sine function, this function is usually called the signum function. Definition The signum function of a real number is a piecewise function which is defined as follows: \sgn x :=\begin -1 & \text x 0. \end Properties Any real number can be expressed as the product of its absolute value and its sign function: x = , x, \sgn x. It follows that whenever is not equal to 0 we have \sgn x = \frac = \frac\,. Similarly, for ''any'' real number , , x, = x\sgn x. We can also ascertain that: \sgn x^n=(\sgn x)^n. The signum function is the derivative of the absolute value function, up to (but not including) the indeterminacy at zero. More formally, in integration theory it is a weak derivative, and in convex function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Second Derivative
In calculus, the second derivative, or the second order derivative, of a function is the derivative of the derivative of . Roughly speaking, the second derivative measures how the rate of change of a quantity is itself changing; for example, the second derivative of the position of an object with respect to time is the instantaneous acceleration of the object, or the rate at which the velocity of the object is changing with respect to time. In Leibniz notation: :\mathbf = \frac = \frac, where ''a'' is acceleration, ''v'' is velocity, ''t'' is time, ''x'' is position, and d is the instantaneous "delta" or change. The last expression \tfrac is the second derivative of position (x) with respect to time. On the graph of a function, the second derivative corresponds to the curvature or concavity of the graph. The graph of a function with a positive second derivative is upwardly concave, while the graph of a function with a negative second derivative curves in the opposite way. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Euclidean Space
Euclidean space is the fundamental space of geometry, intended to represent physical space. Originally, that is, in Euclid's Elements, Euclid's ''Elements'', it was the three-dimensional space of Euclidean geometry, but in modern mathematics there are Euclidean spaces of any positive integer dimension (mathematics), dimension, including the three-dimensional space and the ''Euclidean plane'' (dimension two). The qualifier "Euclidean" is used to distinguish Euclidean spaces from other spaces that were later considered in physics and modern mathematics. Ancient History of geometry#Greek geometry, Greek geometers introduced Euclidean space for modeling the physical space. Their work was collected by the Greek mathematics, ancient Greek mathematician Euclid in his ''Elements'', with the great innovation of ''mathematical proof, proving'' all properties of the space as theorems, by starting from a few fundamental properties, called ''postulates'', which either were considered as eviden ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Function
In mathematics, a continuous function is a function such that a continuous variation (that is a change without jump) of the argument induces a continuous variation of the value of the function. This means that there are no abrupt changes in value, known as '' discontinuities''. More precisely, a function is continuous if arbitrarily small changes in its value can be assured by restricting to sufficiently small changes of its argument. A discontinuous function is a function that is . Up until the 19th century, mathematicians largely relied on intuitive notions of continuity, and considered only continuous functions. The epsilon–delta definition of a limit was introduced to formalize the definition of continuity. Continuity is one of the core concepts of calculus and mathematical analysis, where arguments and values of functions are real and complex numbers. The concept has been generalized to functions between metric spaces and between topological spaces. The latter are the mo ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Darboux Property
In mathematics, Darboux's theorem is a theorem in real analysis, named after Jean Gaston Darboux. It states that every function that results from the differentiation of another function has the intermediate value property: the image of an interval is also an interval. When ''ƒ'' is continuously differentiable (''ƒ'' in ''C''1( 'a'',''b''), this is a consequence of the intermediate value theorem. But even when ''ƒ′'' is ''not'' continuous, Darboux's theorem places a severe restriction on what it can be. Darboux's theorem Let I be a closed interval, f\colon I\to \R be a real-valued differentiable function. Then f' has the intermediate value property: If a and b are points in I with a such that f'(x)=y.Apostol, Tom M.: Mathematical Analysis: A Modern Approach to Advanced Calculus, 2nd edition, Addison-Wesley Longman, Inc. (1974), page 112.Olsen, Lars: ''A New Proof of Darboux's Theorem'', Vol. 111, No. 8 (Oct., 2004) (pp. 713–715), The American Mathematical MonthlyRud ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Secant Line
Secant is a term in mathematics derived from the Latin ''secare'' ("to cut"). It may refer to: * a secant line, in geometry * the secant variety, in algebraic geometry * secant (trigonometry) (Latin: secans), the multiplicative inverse (or reciprocal) trigonometric function of the cosine * the secant method, a root-finding algorithm in numerical analysis, based on secant lines to graphs of functions * a secant ogive Secant is a term in mathematics derived from the Latin ''secare'' ("to cut"). It may refer to: * a secant line, in geometry * the secant variety, in algebraic geometry * secant (trigonometry) (Latin: secans), the multiplicative inverse (or reciproc ... in nose cone design {{mathdab sr:Секанс ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Open Interval
In mathematics, a (real) interval is a set of real numbers that contains all real numbers lying between any two numbers of the set. For example, the set of numbers satisfying is an interval which contains , , and all numbers in between. Other examples of intervals are the set of numbers such that , the set of all real numbers \R, the set of nonnegative real numbers, the set of positive real numbers, the empty set, and any singleton (set of one element). Real intervals play an important role in the theory of integration, because they are the simplest sets whose "length" (or "measure" or "size") is easy to define. The concept of measure can then be extended to more complicated sets of real numbers, leading to the Borel measure and eventually to the Lebesgue measure. Intervals are central to interval arithmetic, a general numerical computing technique that automatically provides guaranteed enclosures for arbitrary formulas, even in the presence of uncertainties, mathematical ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |