|
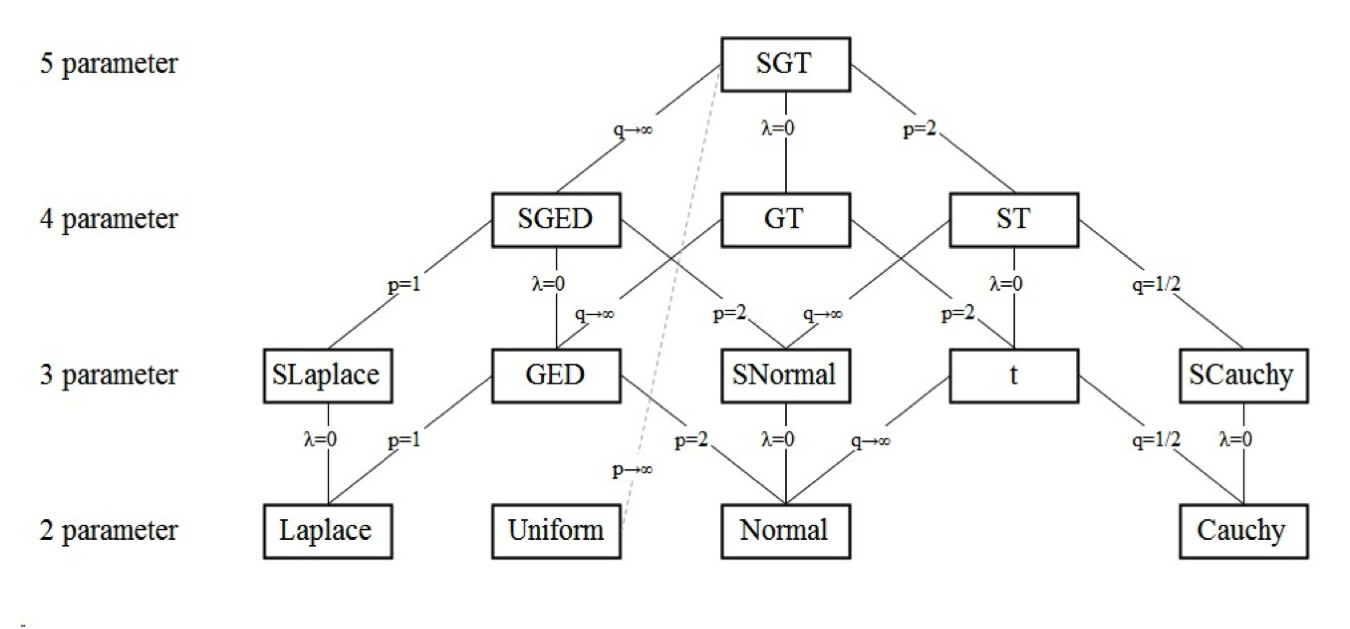
Skewed Generalized T Distribution
In probability and statistics, the skewed generalized "t" distribution is a family of continuous probability distributions. The distribution was first introduced by Panayiotis Theodossiou in 1998. The distribution has since been used in different applications. There are different parameterizations for the skewed generalized t distribution. Definition Probability density function f_\text(x; \mu, \sigma, \lambda, p, q) = \frac where B is the beta function, \mu is the location parameter, \sigma > 0 is the scale parameter, -1 0 are the parameters that control the kurtosis. m and v are not parameters, but functions of the other parameters that are used here to scale or shift the distribution appropriately to match the various parameterizations of this distribution. In the original parameterization of the skewed generalized t distribution, :m = \lambda v \sigma \frac and :v = \frac. These values for m and v yield a distribution with mean of \mu if pq > 1 and a variance of \s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probability
Probability is the branch of mathematics concerning numerical descriptions of how likely an Event (probability theory), event is to occur, or how likely it is that a proposition is true. The probability of an event is a number between 0 and 1, where, roughly speaking, 0 indicates impossibility of the event and 1 indicates certainty."Kendall's Advanced Theory of Statistics, Volume 1: Distribution Theory", Alan Stuart and Keith Ord, 6th Ed, (2009), .William Feller, ''An Introduction to Probability Theory and Its Applications'', (Vol 1), 3rd Ed, (1968), Wiley, . The higher the probability of an event, the more likely it is that the event will occur. A simple example is the tossing of a fair (unbiased) coin. Since the coin is fair, the two outcomes ("heads" and "tails") are both equally probable; the probability of "heads" equals the probability of "tails"; and since no other outcomes are possible, the probability of either "heads" or "tails" is 1/2 (which could also be written ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Skew Normal Distribution
In probability theory and statistics, the skew normal distribution is a continuous probability distribution that generalises the normal distribution to allow for non-zero skewness. Definition Let \phi(x) denote the standard normal probability density function :\phi(x)=\frace^ with the cumulative distribution function given by :\Phi(x) = \int_^ \phi(t)\ dt = \frac \left 1 + \operatorname \left(\frac\right)\right/math>, where "erf" is the error function. Then the probability density function (pdf) of the skew-normal distribution with parameter \alpha is given by :f(x) = 2\phi(x)\Phi(\alpha x). \, This distribution was first introduced by O'Hagan and Leonard (1976). Alternative forms to this distribution, with the corresponding quantile function, have been given by Ashour and Abdel-Hamid and by Mudholkar and Hutson. A stochastic process that underpins the distribution was described by Andel, Netuka and Zvara (1984). Both the distribution and its stochastic process underpinnings ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Normal Distribution
In statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is : f(x) = \frac e^ The parameter \mu is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma is its standard deviation. The variance of the distribution is \sigma^2. A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution converges to a normal dist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Continuous Distributions
Continuity or continuous may refer to: Mathematics * Continuity (mathematics), the opposing concept to discreteness; common examples include ** Continuous probability distribution or random variable in probability and statistics ** Continuous game, a generalization of games used in game theory ** Law of Continuity, a heuristic principle of Gottfried Leibniz * Continuous function, in particular: ** Continuity (topology), a generalization to functions between topological spaces ** Scott continuity, for functions between posets ** Continuity (set theory), for functions between ordinals ** Continuity (category theory), for functors ** Graph continuity, for payoff functions in game theory * Continuity theorem may refer to one of two results: ** Lévy's continuity theorem, on random variables ** Kolmogorov continuity theorem, on stochastic processes * In geometry: ** Parametric continuity, for parametrised curves ** Geometric continuity, a concept primarily applied to the coni ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Management Science (journal)
''For the theoretical and practical problem-solving subfield of Management, see Management Science.'' ''Management Science'' is a peer-reviewed academic journal that covers research on all aspects of management related to strategy, entrepreneurship, innovation, information technology, and organizations as well as all functional areas of business, such as accounting, finance, marketing, and operations. It is published by the Institute for Operations Research and the Management Sciences and was established in 1954 by the institute's precursor, the Institute of Management Sciences. C. West Churchman was the founding editor-in-chief. According to the ''Journal Citation Reports'', the journal has a 2018 impact factor of 4.219. Editors-in-chief The following persons are, or have been, editors-in-chief: *2018–2020: David Simchi-Levi *2014–2018: Teck-Hua Ho *2009–2014: Gérard Cachon *2003–2008: Wallace Hopp *1997–2002: Hau L. Lee *1993–1997: Gabriel R. Bitran *1983– ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Econometric Theory
''Econometric Theory'' is an economics journal specialising in econometrics, published by Cambridge Journals. Its current editor is Peter Phillips Peter Mark Andrew Phillips (born 15 November 1977) is a British businessman and the son of Anne, Princess Royal, and Captain Mark Phillips. He is the eldest nephew of King Charles III, and 17th in the line of succession to the British throne. .... It is one of the main econometrics journals. The journal was founded against a backdrop of strong growth in econometrics research in 1985. At the time of its foundation, a main goal was to support theoretical developments in econometrics. Whereas many early articles focused exclusively on theory, disregarding practical applications, it became standard practice to include empirical illustrations or simulations in recent decades. References * . Also published as University of Cyprus, Department of Economics Working Paper 01-10 External links Econometrics journals Publications e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Of Business And Economic Statistics
The ''Journal of Business & Economic Statistics'' is a quarterly peer-reviewed academic journal published by the American Statistical Association. The journal covers a broad range of applied problems in business and economic statistics, including forecasting, seasonal adjustment, applied demand and cost analysis, applied econometric modeling, empirical finance, analysis of survey and longitudinal data related to business and economic problems, the impact of discrimination on wages and productivity, the returns to education and training, the effects of unionization, and applications of stochastic control theory to business and economic problems. See also *List of scholarly journals in economics The following is a list of scholarly journals in economics containing most of the prominent academic journals in economics. Popular magazines or other publications related to economics, finance, or business are not listed. A *''Affilia'' *' ... References External links Journal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
International Economic Review
The ''International Economic Review'', (IER) is a quarterly peer-reviewed scientific journal in economics published by the Economics Department of the University of Pennsylvania and Osaka University. The journal's focus is wide and includes many areas of economics, including econometrics, economic theory, macroeconomics, and applied economics. IER was started in 1960 by Michio Morishima, at Osaka University's Institute of Social Economic Research (ISER), and Lawrence R. Klein, at the University of Pennsylvania's Wharton School and Department of Economics. The Kansai Economic Federation of Osaka materially and financially supported the IER at its initial stages. In the present, the IER is run as a non-profit joint academic venture between ISER and the Department of Economics at the University of Pennsylvania. The journal is currently edited by Harold L. Cole of the Pennsylvania Editorial Office and co-edited by Charles Yuji Horioka of the Osaka Editorial Office. The chair of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uniform Distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of symmetric probability distributions. The distribution describes an experiment where there is an arbitrary outcome that lies between certain bounds. The bounds are defined by the parameters, ''a'' and ''b'', which are the minimum and maximum values. The interval can either be closed (e.g. , b or open (e.g. (a, b)). Therefore, the distribution is often abbreviated ''U'' (''a'', ''b''), where U stands for uniform distribution. The difference between the bounds defines the interval length; all intervals of the same length on the distribution's support are equally probable. It is the maximum entropy probability distribution for a random variable ''X'' under no constraint other than that it is contained in the distribution's support. Definitions Probability density function The probability density function of the continuous uniform distribution is: : f(x)=\be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-distribution
In probability and statistics, Student's ''t''-distribution (or simply the ''t''-distribution) is any member of a family of continuous probability distributions that arise when estimating the mean of a normally distributed population in situations where the sample size is small and the population's standard deviation is unknown. It was developed by English statistician William Sealy Gosset under the pseudonym "Student". The ''t''-distribution plays a role in a number of widely used statistical analyses, including Student's ''t''-test for assessing the statistical significance of the difference between two sample means, the construction of confidence intervals for the difference between two population means, and in linear regression analysis. Student's ''t''-distribution also arises in the Bayesian analysis of data from a normal family. If we take a sample of n observations from a normal distribution, then the ''t''-distribution with \nu=n-1 degrees of freedom can be d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Normal Distribution
The generalized normal distribution or generalized Gaussian distribution (GGD) is either of two families of parametric continuous probability distributions on the real line. Both families add a shape parameter to the normal distribution. To distinguish the two families, they are referred to below as "symmetric" and "asymmetric"; however, this is not a standard nomenclature. Symmetric version The symmetric generalized normal distribution, also known as the exponential power distribution or the generalized error distribution, is a parametric family of symmetric distributions. It includes all normal and Laplace distributions, and as limiting cases it includes all continuous uniform distributions on bounded intervals of the real line. This family includes the normal distribution when \textstyle\beta=2 (with mean \textstyle\mu and variance \textstyle \frac) and it includes the Laplace distribution when \textstyle\beta=1. As \textstyle\beta\rightarrow\infty, the density con ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |