|
Size Functor
Given a size pair (M,f)\ where M\ is a manifold of dimension n\ and f\ is an arbitrary real continuous function defined on it, the i-th size functor, with i=0,\ldots,n\ , denoted by F_i\ , is the functor in Fun(\mathrm,\mathrm)\ , where \mathrm\ is the category of ordered real numbers, and \mathrm\ is the category of Abelian groups, defined in the following way. For x\le y\ , setting M_x=\\ , M_y=\\ , j_\ equal to the inclusion from M_x\ into M_y\ , and k_\ equal to the morphism in \mathrm\ from x\ to y\ , * for each x\in\R\ , F_i(x)=H_i(M_x);\ * F_i(k_)=H_i(j_).\ In other words, the size functor studies the process of the birth and death of homology classes as the lower level set changes. When M\ is smooth and compact and f\ is a Morse function, the functor F_0\ can be described by oriented trees, called H_0\ − trees. The concept of size functor was introduced as an extension to homology theory and category theory of the idea of size function. The mai ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Pair
In mathematics, size theory studies the properties of topological spaces endowed with \mathbb^k-valued functions, with respect to the change of these functions. More formally, the subject of size theory is the study of the natural pseudodistance between size pairs. A survey of size theory can be found in .Silvia Biasotti, Leila De Floriani, Bianca Falcidieno, Patrizio Frosini, Daniela Giorgi, Claudia Landi, Laura Papaleo, Michela Spagnuolo, Describing shapes by geometrical-topological properties of real functions, ACM Computing Surveys, vol. 40 (2008), n. 4, 12:1–12:87. History and applications The beginning of size theory is rooted in the concept of size function, introduced by Frosini.Patrizio Frosini, ''A distance for similarity classes of submanifolds of a Euclidean space'', Bulletin of the Australian Mathematical Society, 42(3):407–416, 1990. Size functions have been initially used as a mathematical tool for shape comparison in computer vision and pattern reco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
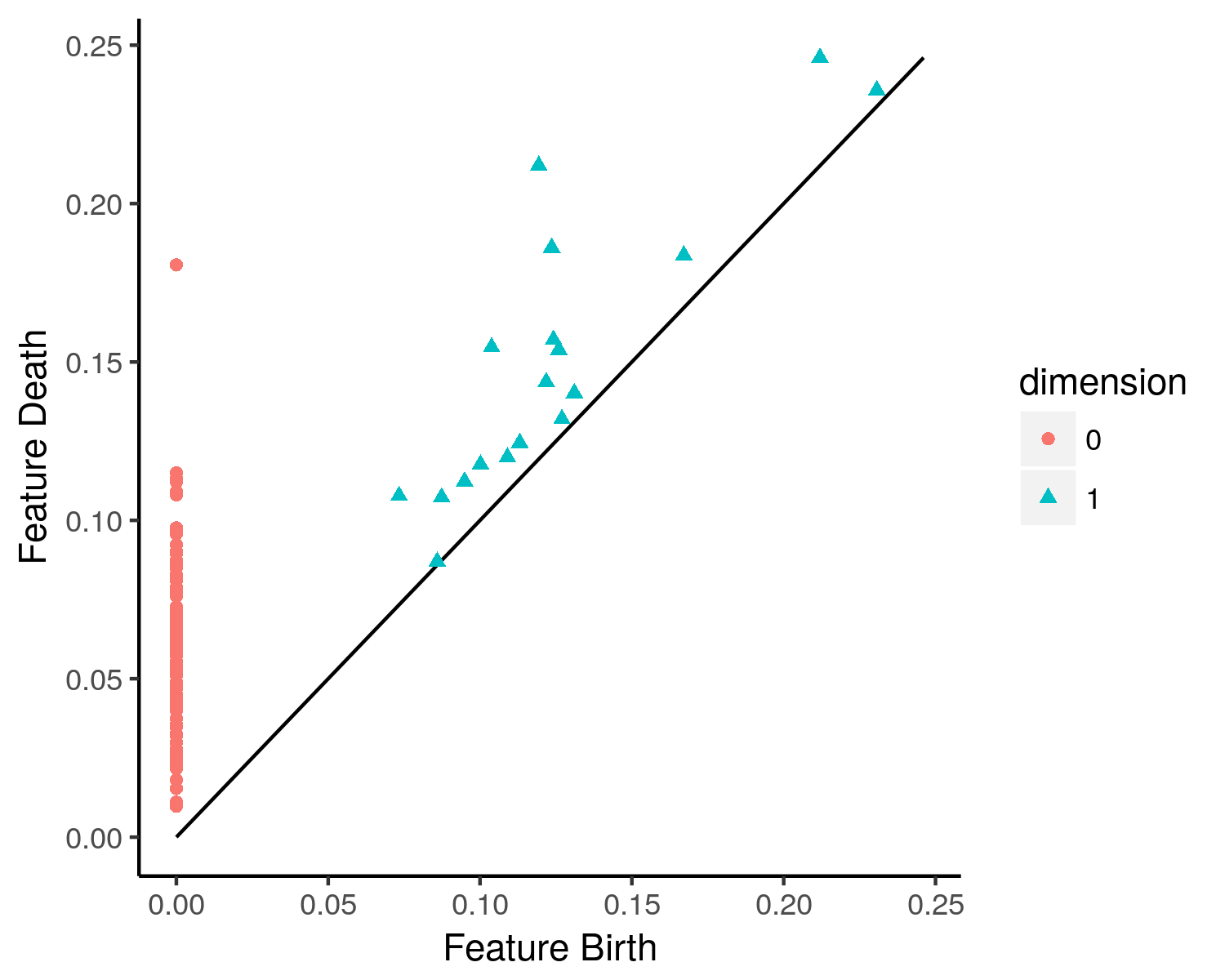
Persistent Homology Group
In persistent homology, a persistent homology group is a multiscale analog of a homology group that captures information about the evolution of topological features across a filtration of spaces. While the ordinary homology group represents nontrivial homology classes of an individual topological space, the persistent homology group tracks only those classes that remain nontrivial across multiple parameters in the underlying filtration. Analogous to the ordinary Betti number, the ranks of the persistent homology groups are known as the persistent Betti numbers. Persistent homology groups were first introduced by Herbert Edelsbrunner, David Letscher, and Afra Zomorodian in a 2002 paper ''Topological Persistence and Simplification'', one of the foundational papers in the fields of persistent homology and topological data analysis, based largely on the persistence barcodes and the persistence algorithm, that were first described by Serguei Barannikov in the 1994 paper. Since t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Pair
In mathematics, size theory studies the properties of topological spaces endowed with \mathbb^k-valued functions, with respect to the change of these functions. More formally, the subject of size theory is the study of the natural pseudodistance between size pairs. A survey of size theory can be found in .Silvia Biasotti, Leila De Floriani, Bianca Falcidieno, Patrizio Frosini, Daniela Giorgi, Claudia Landi, Laura Papaleo, Michela Spagnuolo, Describing shapes by geometrical-topological properties of real functions, ACM Computing Surveys, vol. 40 (2008), n. 4, 12:1–12:87. History and applications The beginning of size theory is rooted in the concept of size function, introduced by Frosini.Patrizio Frosini, ''A distance for similarity classes of submanifolds of a Euclidean space'', Bulletin of the Australian Mathematical Society, 42(3):407–416, 1990. Size functions have been initially used as a mathematical tool for shape comparison in computer vision and pattern reco ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Homotopy Group
The concept of size homotopy group is analogous in size theory of the classical concept of homotopy group. In order to give its definition, let us assume that a size pair (M,\varphi) is given, where M is a closed manifold of class C^0\ and \varphi:M\to \mathbb^k is a continuous function. Consider the lexicographical order \preceq on \mathbb^k defined by setting (x_1,\ldots,x_k)\preceq(y_1,\ldots,y_k)\ if and only if x_1 \le y_1,\ldots, x_k \le y_k. For every Y\in\mathbb^k set M_=\. Assume that P\in M_X\ and X\preceq Y\ . If \alpha\ , \beta\ are two paths from P\ to P\ and a homotopy from \alpha\ to \beta\ , based at P\ , exists in the topological space M_\ , then we write \alpha \approx_\beta\ . The first size homotopy group of the size pair (M,\varphi)\ computed at (X,Y)\ is defined to be the quotient set of the set of all paths from P\ to P\ in M_X\ with respect to the equivalence relation \approx_\ , endowed with the operation induced by the usual composition of base ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane x Formal definition In , the size function associated with the[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Theory
In mathematics, size theory studies the properties of topological spaces endowed with \mathbb^k-valued functions, with respect to the change of these functions. More formally, the subject of size theory is the study of the natural pseudodistance between size pairs. A survey of size theory can be found in .Silvia Biasotti, Leila De Floriani, Bianca Falcidieno, Patrizio Frosini, Daniela Giorgi, Claudia Landi, Laura Papaleo, Michela Spagnuolo, Describing shapes by geometrical-topological properties of real functions, ACM Computing Surveys, vol. 40 (2008), n. 4, 12:1–12:87. History and applications The beginning of size theory is rooted in the concept of size function, introduced by Frosini.Patrizio Frosini, ''A distance for similarity classes of submanifolds of a Euclidean space'', Bulletin of the Australian Mathematical Society, 42(3):407–416, 1990. Size functions have been initially used as a mathematical tool for shape comparison in computer vision and pattern recogn ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Homomorphism
In algebra, a homomorphism is a structure-preserving map between two algebraic structures of the same type (such as two groups, two rings, or two vector spaces). The word ''homomorphism'' comes from the Ancient Greek language: () meaning "same" and () meaning "form" or "shape". However, the word was apparently introduced to mathematics due to a (mis)translation of German meaning "similar" to meaning "same". The term "homomorphism" appeared as early as 1892, when it was attributed to the German mathematician Felix Klein (1849–1925). Homomorphisms of vector spaces are also called linear maps, and their study is the subject of linear algebra. The concept of homomorphism has been generalized, under the name of morphism, to many other structures that either do not have an underlying set, or are not algebraic. This generalization is the starting point of category theory. A homomorphism may also be an isomorphism, an endomorphism, an automorphism, etc. (see below). Eac ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Persistent Homology
:''See homology for an introduction to the notation.'' Persistent homology is a method for computing topological features of a space at different spatial resolutions. More persistent features are detected over a wide range of spatial scales and are deemed more likely to represent true features of the underlying space rather than artifacts of sampling, noise, or particular choice of parameters. To find the persistent homology of a space, the space must first be represented as a simplicial complex. A distance function on the underlying space corresponds to a filtration of the simplicial complex, that is a nested sequence of increasing subsets. Definition Formally, consider a real-valued function on a simplicial complex f:K \rightarrow \mathbb that is non-decreasing on increasing sequences of faces, so f(\sigma) \leq f(\tau) whenever \sigma is a face of \tau in K. Then for every a \in \mathbb the sublevel set K_a=f^((-\infty, a]) is a subcomplex of ''K'', and the ordering of the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Discrete & Computational Geometry
'' Discrete & Computational Geometry'' is a peer-reviewed mathematics journal published quarterly by Springer. Founded in 1986 by Jacob E. Goodman and Richard M. Pollack, the journal publishes articles on discrete geometry and computational geometry. Abstracting and indexing The journal is indexed in: * ''Mathematical Reviews'' * ''Zentralblatt MATH'' * ''Science Citation Index The Science Citation Index Expanded – previously entitled Science Citation Index – is a citation index originally produced by the Institute for Scientific Information (ISI) and created by Eugene Garfield. It was officially launched in 1964 ...'' * '' Current Contents''/Engineering, Computing and Technology Notable articles The articles by Gil Kalai with a proof of a subexponential upper bound on the diameter of a polyhedron and by Samuel Ferguson on the Kepler conjecture, both published in Discrete & Computational geometry, earned their author the Fulkerson Prize. References Externa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Size Function
Size functions are shape descriptors, in a geometrical/topological sense. They are functions from the half-plane x Formal definition In , the size function associated with the[...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Manifold
In mathematics, a manifold is a topological space that locally resembles Euclidean space near each point. More precisely, an n-dimensional manifold, or ''n-manifold'' for short, is a topological space with the property that each point has a neighborhood that is homeomorphic to an open subset of n-dimensional Euclidean space. One-dimensional manifolds include lines and circles, but not lemniscates. Two-dimensional manifolds are also called surfaces. Examples include the plane, the sphere, and the torus, and also the Klein bottle and real projective plane. The concept of a manifold is central to many parts of geometry and modern mathematical physics because it allows complicated structures to be described in terms of well-understood topological properties of simpler spaces. Manifolds naturally arise as solution sets of systems of equations and as graphs of functions. The concept has applications in computer-graphics given the need to associate pictures with coordinates ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Category Theory
Category theory is a general theory of mathematical structures and their relations that was introduced by Samuel Eilenberg and Saunders Mac Lane in the middle of the 20th century in their foundational work on algebraic topology. Nowadays, category theory is used in almost all areas of mathematics, and in some areas of computer science. In particular, many constructions of new mathematical objects from previous ones, that appear similarly in several contexts are conveniently expressed and unified in terms of categories. Examples include quotient spaces, direct products, completion, and duality. A category is formed by two sorts of objects: the objects of the category, and the morphisms, which relate two objects called the ''source'' and the ''target'' of the morphism. One often says that a morphism is an ''arrow'' that ''maps'' its source to its target. Morphisms can be ''composed'' if the target of the first morphism equals the source of the second one, and morphism com ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |