|
Probit
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables. Mathematically, the probit is the inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96 and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, generating a value of a standard normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probit Plot
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular Q–Q plot, exploratory statistical graphics and specialized probit model, regression modeling of binary response variables. Mathematically, the probit is the inverse function, inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96 and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Probit Model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to estimate the probability that an observation with particular characteristics will fall into a specific one of the categories; moreover, classifying observations based on their predicted probabilities is a type of binary classification model. A probit model is a popular specification for a binary response model. As such it treats the same set of problems as does logistic regression using similar techniques. When viewed in the generalized linear model framework, the probit model employs a probit link function. It is most often estimated using the maximum likelihood procedure, such an estimation being called a probit regression. Conceptual framework Suppose a response variable ''Y'' is ''binary'', that is it can have only two possible o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logistic Regression
In statistics, a logistic model (or logit model) is a statistical model that models the logit, log-odds of an event as a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) estimation theory, estimates the parameters of a logistic model (the coefficients in the linear or non linear combinations). In binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logit Model
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations. Mathematically, the logit is the inverse of the standard logistic function \sigma(x) = 1/(1+e^), so the logit is defined as : \operatorname p = \sigma^(p) = \ln \frac \quad \text \quad p \in (0,1). Because of this, the logit is also called the log-odds since it is equal to the logarithm of the odds \frac where is a probability. Thus, the logit is a type of function that maps probability values from (0, 1) to real numbers in (-\infty, +\infty), akin to the probit function. Definition If is a probability, then is the corresponding odds; the of the probability is the logarithm of the odds, i.e.: : \operatorname(p)=\ln\left( \frac \right) =\ln(p)-\ln(1-p)=-\ln\left( \frac-1\right)=2\operatorname(2p-1). The base of the logarithm function used is of little import ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Logit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in Data transformation (statistics), data transformations. Mathematically, the logit is the inverse function, inverse of the logistic function, standard logistic function \sigma(x) = 1/(1+e^), so the logit is defined as : \operatorname p = \sigma^(p) = \ln \frac \quad \text \quad p \in (0,1). Because of this, the logit is also called the log-odds since it is equal to the logarithm of the odds \frac where is a probability. Thus, the logit is a type of function that maps probability values from (0, 1) to real numbers in (-\infty, +\infty), akin to the probit, probit function. Definition If is a probability, then is the corresponding odds; the of the probability is the logarithm of the odds, i.e.: : \operatorname(p)=\ln\left( \frac \right) =\ln(p)-\ln(1-p)=-\ln\left( \frac-1\right)=2\operatornam ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quanti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
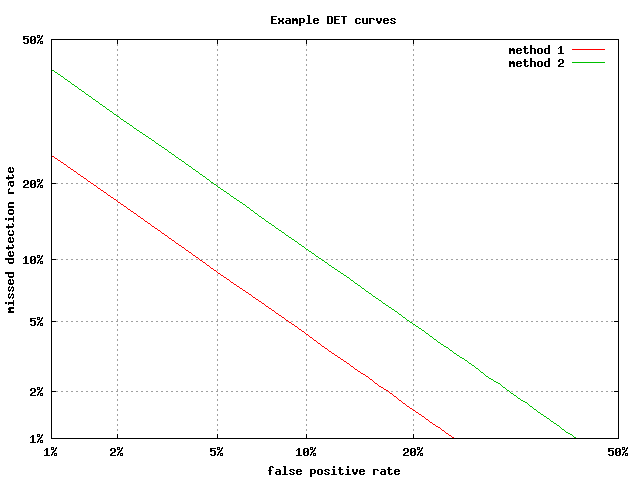
Detection Error Tradeoff
A detection error tradeoff (DET) graph is a graphical plot of error rates for binary classifier , binary classification systems, plotting the false rejection rate vs. false acceptance rate.A. Martin, A., G. Doddington, T. Kamm, M. Ordowski, and M. Przybocki.The DET Curve in Assessment of Detection Task Performance, Proc. Eurospeech '97, Rhodes, Greece, September 1997, Vol. 4, pp. 1895-1898. The x- and y-axes are scaled non-linearly by their standard normal deviates (or just by logarithmic transformation), yielding tradeoff curves that are more linear than Receiver operating characteristic , ROC curves, and use most of the image area to highlight the differences of importance in the critical operating region. Axis warping The normal deviate mapping (or normal quantile function, or inverse normal cumulative distribution) is given by the probit, probit function, so that the horizontal axis is ''x'' = probit(''Pfa'') and the vertical is ''y'' = probit(''Pfr''), where ''Pfa'' and ''Pf ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Chester Ittner Bliss
Chester Ittner Bliss (February 1, 1899 – March 14, 1979) was primarily a biologist, who is best known for his contributions to statistics. He was born in Springfield, Ohio in 1899 and died in 1979. He was the first secretary of the International Biometric Society. Academic qualifications *Bachelor of Arts in Entomology from Ohio State University, 1921 *Master of Arts from Columbia University, 1922 *PhD from Columbia University, 1926 Remarkably, his statistical knowledge was largely self-taught and developed according to the problems he wanted to solve (Cochran & Finney 1979). Nevertheless, in 1942 he was elected as a Fellow of the American Statistical Association. Major contributions The idea of the probit function was published by Bliss in a 1934 article in ''Science'' on how to treat data such as the percentage of a pest killed by a pesticide. Bliss proposed transforming the percentage killed into a "probability unit" (or "probit"). Arguably his most important contributi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Normal Distribution
In probability theory and statistics, a normal distribution or Gaussian distribution is a type of continuous probability distribution for a real-valued random variable. The general form of its probability density function is f(x) = \frac e^\,. The parameter is the mean or expectation of the distribution (and also its median and mode), while the parameter \sigma^2 is the variance. The standard deviation of the distribution is (sigma). A random variable with a Gaussian distribution is said to be normally distributed, and is called a normal deviate. Normal distributions are important in statistics and are often used in the natural and social sciences to represent real-valued random variables whose distributions are not known. Their importance is partly due to the central limit theorem. It states that, under some conditions, the average of many samples (observations) of a random variable with finite mean and variance is itself a random variable—whose distribution c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a function \mathrm: \mathbb \to \mathbb defined as: \operatorname z = \frac\int_0^z e^\,\mathrm dt. The integral here is a complex Contour integration, contour integral which is path-independent because \exp(-t^2) is Holomorphic function, holomorphic on the whole complex plane \mathbb. In many applications, the function argument is a real number, in which case the function value is also real. In some old texts, the error function is defined without the factor of \frac. This nonelementary integral is a sigmoid function, sigmoid function that occurs often in probability, statistics, and partial differential equations. In statistics, for non-negative real values of , the error function has the following interpretation: for a real random variable that is normal distribution, normally distributed with mean 0 and standard deviation \frac, is the probability that falls in the range . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Quantile Function
In probability and statistics, the quantile function is a function Q: ,1\mapsto \mathbb which maps some probability x \in ,1/math> of a random variable v to the value of the variable y such that P(v\leq y) = x according to its probability distribution. In other words, the function returns the value of the variable below which the specified cumulative probability is contained. For example, if the distribution is a standard normal distribution then Q(0.5) will return 0 as 0.5 of the probability mass is contained below 0. The quantile function is also called the percentile function (after the percentile), percent-point function, inverse cumulative distribution function (after the cumulative distribution function or c.d.f.) or inverse distribution function. Definition Strictly increasing distribution function With reference to a continuous and strictly increasing cumulative distribution function (c.d.f.) F_X\colon \mathbb \to ,1/math> of a random variable , the quantile function ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |