|
Power Sum
In mathematics and statistics, sums of powers occur in a number of contexts: * Sums of squares arise in many contexts. For example, in geometry, the Pythagorean theorem involves the sum of two squares; in number theory, there are Legendre's three-square theorem and Jacobi's four-square theorem; and in statistics, the analysis of variance involves summing the squares of quantities. *Faulhaber's formula expresses 1^k + 2^k + 3^k + \cdots + n^k as a polynomial in ''n'', or alternatively in term of a Bernoulli polynomial. *Fermat's right triangle theorem states that there is no solution in positive integers for a^2=b^4+c^4 and a^4=b^4+c^2. *Fermat's Last Theorem states that x^k+y^k=z^k is impossible in positive integers with ''k''>2. *The equation of a superellipse is , x/a, ^k+, y/b, ^k=1. The squircle is the case k=4, a=b. *Euler's sum of powers conjecture (disproved) concerns situations in which the sum of ''n'' integers, each a ''k''th power of an integer, equals another ''k''th po ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Beal's Conjecture
The Beal conjecture is the following conjecture in number theory: :If :: A^x +B^y = C^z, :where ''A'', ''B'', ''C'', ''x'', ''y'', and ''z'' are positive integers with ''x'', ''y'', ''z'' ≥ 3, then ''A'', ''B'', and ''C'' have a common prime factor. Equivalently, :The equation A^x + B^y = C^z has no solutions in positive integers and pairwise coprime integers ''A, B, C'' if ''x, y, z'' ≥ 3. The conjecture was formulated in 1993 by Andrew Beal, a banker and amateur mathematician, while investigating generalizations of Fermat's Last Theorem. Since 1997, Beal has offered a monetary prize for a peer-reviewed proof of this conjecture or a counterexample. The value of the prize has increased several times and is currently $1 million. In some publications, this conjecture has occasionally been referred to as a generalized Fermat equation, the Mauldin conjecture, and the Tijdeman-Zagier conjecture. Related examples To illustrate, the solution 3^3 + 6^3 = 3^5 has bases with a c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Erdős–Moser Equation
In number theory, the Erdős–Moser equation is :1^k+2^k+\cdots+m^k=(m+1)^k, where m and k are positive integers. The only known solution is 11 + 21 = 31, and Paul Erdős conjectured that no further solutions exist. Constraints on solutions Leo Moser in 1953 proved that, in any further solutions, 2 must divide ''k'' and that ''m'' ≥ 101,000,000. In 1966, it was shown that 6 ≤ ''k'' + 2 1.485 × 109,321,155. In 2002, it was shown that all primes between 200 and 1000 must divide ''k''. In 2009, it was shown that 2''k'' / (2''m'' – 3) must be a convergent (continued fraction), convergent of Natural logarithm of 2, ln(2); large-scale computation of ln(2) was then used to show that ''m'' > 2.7139 × 101,667,658,416. References {{DEFAULTSORT:Erdős-Moser equation Diophantine equations Paul Erdős, Moser equation Unsolved problems in number theory ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
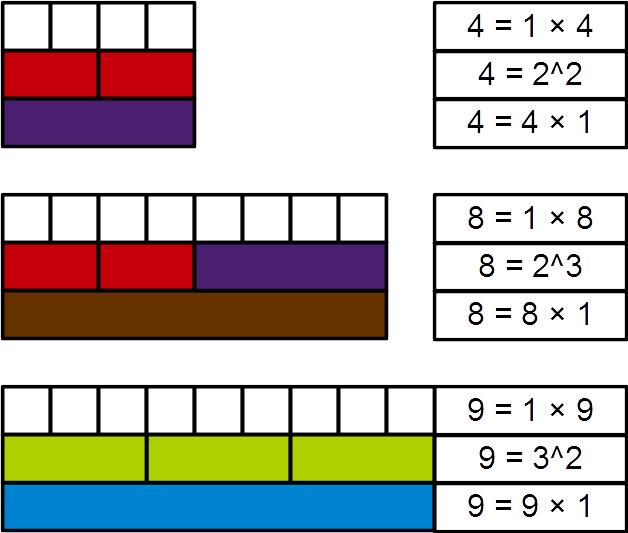
Perfect Power
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, ''n'' is a perfect power if there exist natural numbers ''m'' > 1, and ''k'' > 1 such that ''mk'' = ''n''. In this case, ''n'' may be called a perfect ''k''th power. If ''k'' = 2 or ''k'' = 3, then ''n'' is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0''k'' = 0 for any ''k'' > 0, 1''k'' = 1 for any ''k''). Examples and sums A sequence of perfect powers can be generated by iterating through the possible values for ''m'' and ''k''. The first few ascending perfect powers in numerical order (showing duplicate powers) are : : 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots The sum of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Power Sum Symmetric Polynomial
In mathematics, specifically in commutative algebra, the power sum symmetric polynomials are a type of basic building block for symmetric polynomials, in the sense that every symmetric polynomial with rational coefficients can be expressed as a sum and difference of products of power sum symmetric polynomials with rational coefficients. However, not every symmetric polynomial with integral coefficients is generated by integral combinations of products of power-sum polynomials: they are a generating set over the ''rationals,'' but not over the ''integers.'' Definition The power sum symmetric polynomial of degree ''k'' in n variables ''x''1, ..., ''x''''n'', written ''p''''k'' for ''k'' = 0, 1, 2, ..., is the sum of all ''k''th powers of the variables. Formally, : p_k (x_1, x_2, \dots,x_n) = \sum_^n x_i^k \, . The first few of these polynomials are :p_0 (x_1, x_2, \dots,x_n) = 1 + 1 + \cdots + 1 = n \, , :p_1 (x_1, x_2, \dots,x_n) = x_1 + x_2 + \cdots + x_n \, , :p_2 (x_1, x_2, \d ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fermat Cubic
In geometry, the Fermat cubic, named after Pierre de Fermat, is a surface defined by : x^3 + y^3 + z^3 = 1. \ Methods of algebraic geometry Algebraic geometry is a branch of mathematics, classically studying zeros of multivariate polynomials. Modern algebraic geometry is based on the use of abstract algebraic techniques, mainly from commutative algebra, for solving geometrical ... provide the following parameterization of Fermat's cubic: : x(s,t) = : y(s,t) = : z(s,t) = . In projective space the Fermat cubic is given by :w^3+x^3+y^3+z^3=0. The 27 lines lying on the Fermat cubic are easy to describe explicitly: they are the 9 lines of the form (''w'' : ''aw'' : ''y'' : ''by'') where ''a'' and ''b'' are fixed numbers with cube −1, and their 18 conjugates under permutations of coordinates. ::::''Real points of Fermat cubic surface.'' References * * Algebraic surfaces {{algebraic-geometry-stub ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cube (algebra)
In arithmetic and algebra, the cube of a number is its third power, that is, the result of multiplying three instances of together. The cube of a number or any other mathematical expression is denoted by a superscript 3, for example or . The cube is also the number multiplied by its square: :. The ''cube function'' is the function (often denoted ) that maps a number to its cube. It is an odd function, as :. The volume of a geometric cube is the cube of its side length, giving rise to the name. The inverse operation that consists of finding a number whose cube is is called extracting the cube root of . It determines the side of the cube of a given volume. It is also raised to the one-third power. The graph of the cube function is known as the cubic parabola. Because the cube function is an odd function, this curve has a center of symmetry at the origin, but no axis of symmetry. In integers A cube number, or a perfect cube, or sometimes just a cube, is a number wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Newton's Identities
In mathematics, Newton's identities, also known as the Girard–Newton formulae, give relations between two types of symmetric polynomials, namely between power sums and elementary symmetric polynomials. Evaluated at the roots of a monic polynomial ''P'' in one variable, they allow expressing the sums of the ''k''-th powers of all roots of ''P'' (counted with their multiplicity) in terms of the coefficients of ''P'', without actually finding those roots. These identities were found by Isaac Newton around 1666, apparently in ignorance of earlier work (1629) by Albert Girard. They have applications in many areas of mathematics, including Galois theory, invariant theory, group theory, combinatorics, as well as further applications outside mathematics, including general relativity. Mathematical statement Formulation in terms of symmetric polynomials Let ''x''1, ..., ''x''''n'' be variables, denote for ''k'' ≥ 1 by ''p''''k''(''x''1, ..., ''x''''n'') the ''k''-th power ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Golden Ratio
In mathematics, two quantities are in the golden ratio if their ratio is the same as the ratio of their sum to the larger of the two quantities. Expressed algebraically, for quantities a and b with a > b > 0, where the Greek letter phi ( or \phi) denotes the golden ratio. The constant \varphi satisfies the quadratic equation \varphi^2 = \varphi + 1 and is an irrational number with a value of The golden ratio was called the extreme and mean ratio by Euclid, and the divine proportion by Luca Pacioli, and also goes by several other names. Mathematicians have studied the golden ratio's properties since antiquity. It is the ratio of a regular pentagon's diagonal to its side and thus appears in the construction of the dodecahedron and icosahedron. A golden rectangle—that is, a rectangle with an aspect ratio of \varphi—may be cut into a square and a smaller rectangle with the same aspect ratio. The golden ratio has been used to analyze the proportions of natural object ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Waring's Problem
In number theory, Waring's problem asks whether each natural number ''k'' has an associated positive integer ''s'' such that every natural number is the sum of at most ''s'' natural numbers raised to the power ''k''. For example, every natural number is the sum of at most 4 squares, 9 cubes, or 19 fourth powers. Waring's problem was proposed in 1770 by Edward Waring, after whom it is named. Its affirmative answer, known as the Hilbert–Waring theorem, was provided by Hilbert in 1909. Waring's problem has its own Mathematics Subject Classification, 11P05, "Waring's problem and variants". Relationship with Lagrange's four-square theorem Long before Waring posed his problem, Diophantus had asked whether every positive integer could be represented as the sum of four perfect squares greater than or equal to zero. This question later became known as Bachet's conjecture, after the 1621 translation of Diophantus by Claude Gaspard Bachet de Méziriac, and it was solved by Joseph-Louis Lag ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Lander, Parkin, And Selfridge Conjecture
The Lander, Parkin, and Selfridge conjecture concerns the integer solutions of equations which contain sums of like powers. The equations are generalisations of those considered in Fermat's Last Theorem. The conjecture is that if the sum of some ''k''-th powers equals the sum of some other ''k''-th powers, then the total number of terms in both sums combined must be at least ''k''. Background Diophantine equations, such as the integer version of the equation ''a''2 + ''b''2 = ''c''2 that appears in the Pythagorean theorem, have been studied for their integer solution properties for centuries. Fermat's Last Theorem states that for powers greater than 2, the equation ''a''''k'' + ''b''''k'' = ''c''''k'' has no solutions in non-zero integers ''a'', ''b'', ''c''. Extending the number of terms on either or both sides, and allowing for higher powers than 2, led to Leonhard Euler to propose in 1769 that for all integers ''n'' and ''k'' greater than 1, if the sum of ''n'' ''k''th powe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Riemann Zeta Function
The Riemann zeta function or Euler–Riemann zeta function, denoted by the Greek letter (zeta), is a mathematical function of a complex variable defined as \zeta(s) = \sum_^\infty \frac = \frac + \frac + \frac + \cdots for \operatorname(s) > 1 and its analytic continuation elsewhere. The Riemann zeta function plays a pivotal role in analytic number theory, and has applications in physics, probability theory, and applied statistics. Leonhard Euler first introduced and studied the function over the reals in the first half of the eighteenth century. Bernhard Riemann's 1859 article "On the Number of Primes Less Than a Given Magnitude" extended the Euler definition to a complex variable, proved its meromorphic continuation and functional equation, and established a relation between its zeros and the distribution of prime numbers. This paper also contained the Riemann hypothesis, a conjecture about the distribution of complex zeros of the Riemann zeta function that is consid ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |