|
Porous Medium Equation
The porous medium equation, also called the nonlinear heat equation, is a nonlinear partial differential equation taking the form:where \Delta is the Laplace operator. It may also be put into its equivalent divergence form: = \nabla \cdot \left D(u)\nabla u \right/math>where D(u) = mu^ may be interpreted as a diffusion coefficient and \nabla\cdot(\cdot) is the divergence operator. Solutions Despite being a nonlinear equation, the porous medium equation may be solved exactly using separation of variables or a similarity solution. However, the separation of variables solution is known to blow up to infinity at a finite time. Barenblatt-Kompaneets-Zeldovich similarity solution The similarity approach to solving the porous medium equation was taken by Barenblatt and Kompaneets/Zeldovich, which for x \in \mathbb^ was to find a solution satisfying:u(t,x) = v\left( \right), \quad t > 0for some unknown function v and unknown constants \alpha,\beta. The final solution to the porous me ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinear Partial Differential Equation
In mathematics and physics, a nonlinear partial differential equation is a partial differential equation with nonlinear system, nonlinear terms. They describe many different physical systems, ranging from gravitation to fluid dynamics, and have been used in mathematics to solve problems such as the Poincaré conjecture and the Calabi conjecture. They are difficult to study: almost no general techniques exist that work for all such equations, and usually each individual equation has to be studied as a separate problem. The distinction between a linear and a nonlinear partial differential equation is usually made in terms of the properties of the Operator (mathematics), operator that defines the PDE itself. Methods for studying nonlinear partial differential equations Existence and uniqueness of solutions A fundamental question for any PDE is the existence and uniqueness of a solution for given boundary conditions. For nonlinear equations these questions are in general very hard: f ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hydrogeology
Hydrogeology (''hydro-'' meaning water, and ''-geology'' meaning the study of the Earth) is the area of geology that deals with the distribution and movement of groundwater in the soil and rocks of the Earth's crust (commonly in aquifers). The terms groundwater hydrology, geohydrology, and hydrogeology are often used interchangeably. Hydrogeology is the study of the laws governing the movement of subterranean water, the mechanical, chemical, and thermal interaction of this water with the porous solid, and the transport of energy, chemical constituents, and particulate matter by flow (Domenico and Schwartz, 1998). Groundwater engineering, another name for hydrogeology, is a branch of engineering which is concerned with groundwater movement and design of wells, pumps, and drains. The main concerns in groundwater engineering include groundwater contamination, conservation of supplies, and water quality.Walton, William C. (November 1990). ''Principles of Groundwater Engin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion
Diffusion is the net movement of anything (for example, atoms, ions, molecules, energy) generally from a region of higher concentration to a region of lower concentration. Diffusion is driven by a gradient in Gibbs free energy or chemical potential. It is possible to diffuse "uphill" from a region of lower concentration to a region of higher concentration, like in spinodal decomposition. The concept of diffusion is widely used in many fields, including physics (particle diffusion), chemistry, biology, sociology, economics, and finance (diffusion of people, ideas, and price values). The central idea of diffusion, however, is common to all of these: a substance or collection undergoing diffusion spreads out from a point or location at which there is a higher concentration of that substance or collection. A gradient is the change in the value of a quantity, for example, concentration, pressure, or temperature with the change in another variable, usually distance. A change in c ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Differential Equations
In mathematics, a partial differential equation (PDE) is an equation which imposes relations between the various partial derivatives of a multivariable function. The function is often thought of as an "unknown" to be solved for, similarly to how is thought of as an unknown number to be solved for in an algebraic equation like . However, it is usually impossible to write down explicit formulas for solutions of partial differential equations. There is, correspondingly, a vast amount of modern mathematical and scientific research on methods to numerically approximate solutions of certain partial differential equations using computers. Partial differential equations also occupy a large sector of pure mathematical research, in which the usual questions are, broadly speaking, on the identification of general qualitative features of solutions of various partial differential equations, such as existence, uniqueness, regularity, and stability. Among the many open questions are the e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Porous Medium
A porous medium or a porous material is a material containing pores (voids). The skeletal portion of the material is often called the "matrix" or "frame". The pores are typically filled with a fluid (liquid or gas). The skeletal material is usually a solid, but structures like foams are often also usefully analyzed using concept of porous media. A porous medium is most often characterised by its porosity. Other properties of the medium (e.g. permeability, tensile strength, electrical conductivity, tortuosity) can sometimes be derived from the respective properties of its constituents (solid matrix and fluid) and the media porosity and pores structure, but such a derivation is usually complex. Even the concept of porosity is only straightforward for a poroelastic medium. Often both the solid matrix and the pore network (also known as the pore space) are continuous, so as to form two interpenetrating continua such as in a sponge. However, there is also a concept of closed porosit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diffusion Equation
The diffusion equation is a parabolic partial differential equation. In physics, it describes the macroscopic behavior of many micro-particles in Brownian motion, resulting from the random movements and collisions of the particles (see Fick's laws of diffusion). In mathematics, it is related to Markov processes, such as random walks, and applied in many other fields, such as materials science, information theory, and biophysics. The diffusion equation is a special case of the convection–diffusion equation, when bulk velocity is zero. It is equivalent to the heat equation under some circumstances. Statement The equation is usually written as: where is the density of the diffusing material at location and time and is the collective diffusion coefficient for density at location ; and represents the vector differential operator del. If the diffusion coefficient depends on the density then the equation is nonlinear, otherwise it is linear. The equation above applies wh ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plasma (physics)
Plasma () 1, where \nu_ is the electron gyrofrequency and \nu_ is the electron collision rate. It is often the case that the electrons are magnetized while the ions are not. Magnetized plasmas are ''anisotropic'', meaning that their properties in the direction parallel to the magnetic field are different from those perpendicular to it. While electric fields in plasmas are usually small due to the plasma high conductivity, the electric field associated with a plasma moving with velocity \mathbf in the magnetic field \mathbf is given by the usual Lorentz force, Lorentz formula \mathbf = -\mathbf\times\mathbf, and is not affected by Debye shielding. Mathematical descriptions To completely describe the state of a plasma, all of the particle locations and velocities that describe the electromagnetic field in the plasma region would need to be written down. However, it is generally not practical or necessary to keep track of all the particles in a plasma. Therefore, plasma physicist ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thermal Conductivity
The thermal conductivity of a material is a measure of its ability to conduct heat. It is commonly denoted by k, \lambda, or \kappa. Heat transfer occurs at a lower rate in materials of low thermal conductivity than in materials of high thermal conductivity. For instance, metals typically have high thermal conductivity and are very efficient at conducting heat, while the opposite is true for insulating materials like Rockwool or Styrofoam. Correspondingly, materials of high thermal conductivity are widely used in heat sink applications, and materials of low thermal conductivity are used as thermal insulation. The reciprocal of thermal conductivity is called thermal resistivity. The defining equation for thermal conductivity is \mathbf = - k \nabla T, where \mathbf is the heat flux, k is the thermal conductivity, and \nabla T is the temperature gradient. This is known as Fourier's Law for heat conduction. Although commonly expressed as a scalar, the most general form of th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
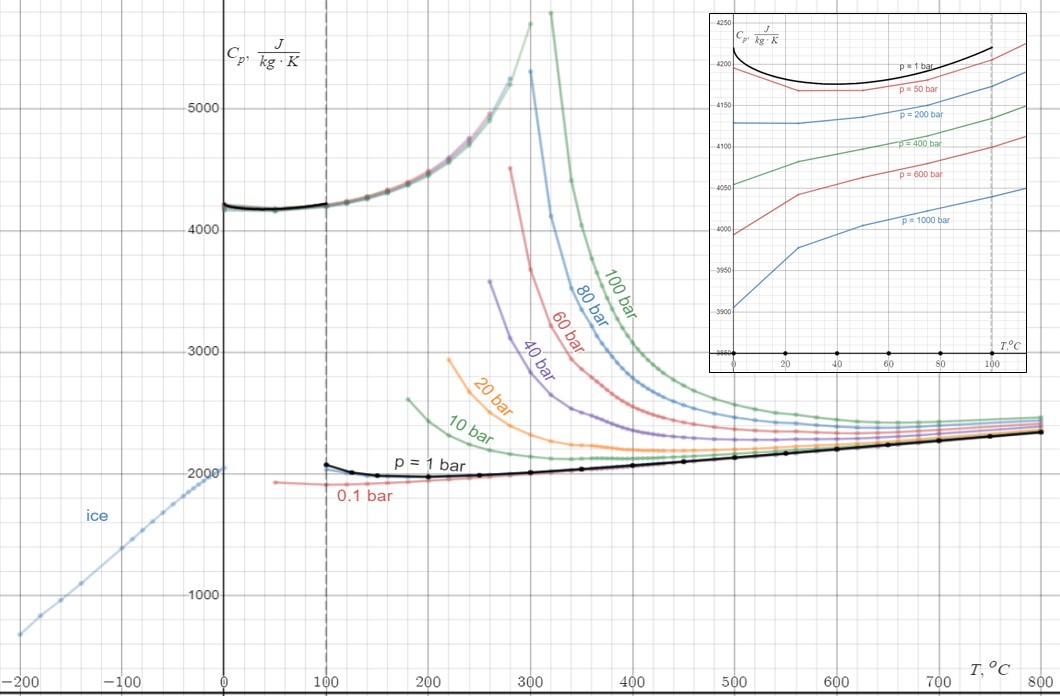
Heat Capacity
Heat capacity or thermal capacity is a physical property of matter, defined as the amount of heat to be supplied to an object to produce a unit change in its temperature. The SI unit of heat capacity is joule per kelvin (J/K). Heat capacity is an extensive property. The corresponding intensive property is the specific heat capacity, found by dividing the heat capacity of an object by its mass. Dividing the heat capacity by the amount of substance in moles yields its molar heat capacity. The volumetric heat capacity measures the heat capacity per volume. In architecture and civil engineering, the heat capacity of a building is often referred to as its thermal mass. Definition Basic definition The heat capacity of an object, denoted by C, is the limit : C = \lim_\frac, where \Delta Q is the amount of heat that must be added to the object (of mass ''M'') in order to raise its temperature by \Delta T. The value of this parameter usually varies considerably depending on the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fourier's Law Of Heat Conduction
Conduction is the process by which heat is transferred from the hotter end to the colder end of an object. The ability of the object to conduct heat is known as its ''thermal conductivity'', and is denoted . Heat spontaneously flows along a temperature gradient (i.e. from a hotter body to a colder body). For example, heat is conducted from the hotplate of an electric stove to the bottom of a saucepan in contact with it. In the absence of an opposing external driving energy source, within a body or between bodies, temperature differences decay over time, and thermal equilibrium is approached, temperature becoming more uniform. In conduction, the heat flow is within and through the body itself. In contrast, in heat transfer by thermal radiation, the transfer is often between bodies, which may be separated spatially. Heat can also be transferred by a combination of conduction and radiation. In solids, conduction is mediated by the combination of vibrations and collisions of molecul ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Isentropic Process
In thermodynamics, an isentropic process is an idealized thermodynamic process that is both adiabatic and reversible. The work transfers of the system are frictionless, and there is no net transfer of heat or matter. Such an idealized process is useful in engineering as a model of and basis of comparison for real processes. This process is idealized because reversible processes do not occur in reality; thinking of a process as both adiabatic and reversible would show that the initial and final entropies are the same, thus, the reason it is called isentropic (entropy does not change). Thermodynamic processes are named based on the effect they would have on the system (ex. isovolumetric: constant volume, isenthalpic: constant enthalpy). Even though in reality it is not necessarily possible to carry out an isentropic process, some may be approximated as such. The word "isentropic" can be interpreted in another way, since its meaning is deducible from its etymology. It means a pro ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |