|
Pitchfork Bifurcation
In bifurcation theory, a field within mathematics, a pitchfork bifurcation is a particular type of local bifurcation theory, bifurcation where the system transitions from one fixed point to three fixed points. Pitchfork bifurcations, like Hopf bifurcations, have two types – supercritical and subcritical. In continuous dynamical systems described by Ordinary differential equation, ODEs—i.e. flows—pitchfork bifurcations occur generically in systems with symmetry in mathematics, symmetry. Supercritical case The normal form (bifurcation theory), normal form of the supercritical pitchfork bifurcation is : \frac=rx-x^3. For r0 there is an unstable equilibrium at x = 0, and two stable equilibria at x = \pm\sqrt. Subcritical case The normal form (bifurcation theory), normal form for the subcritical case is : \frac=rx+x^3. In this case, for r0 the equilibrium at x=0 is unstable. Formal definition An ODE : \dot=f(x,r)\, described by a one parameter function f(x, r) wit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bifurcation Theory
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematics, mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by Ordinary differential equation, ordinary, Delay differential equation, delay or Partial differential equation, partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Mathematics
Mathematics is a field of study that discovers and organizes methods, Mathematical theory, theories and theorems that are developed and Mathematical proof, proved for the needs of empirical sciences and mathematics itself. There are many areas of mathematics, which include number theory (the study of numbers), algebra (the study of formulas and related structures), geometry (the study of shapes and spaces that contain them), Mathematical analysis, analysis (the study of continuous changes), and set theory (presently used as a foundation for all mathematics). Mathematics involves the description and manipulation of mathematical object, abstract objects that consist of either abstraction (mathematics), abstractions from nature orin modern mathematicspurely abstract entities that are stipulated to have certain properties, called axioms. Mathematics uses pure reason to proof (mathematics), prove properties of objects, a ''proof'' consisting of a succession of applications of in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Hopf Bifurcation
In the mathematics of dynamical systems and differential equations, a Hopf bifurcation is said to occur when varying a parameter of the system causes the set of solutions (trajectories) to change from being attracted to (or repelled by) a fixed point, and instead become attracted to (or repelled by) an oscillatory, periodic solution. The Hopf bifurcation is a two-dimensional analog of the pitchfork bifurcation. Many different kinds of systems exhibit Hopf bifurcations, from radio oscillators to railroad bogies. Trailers towed behind automobiles become infamously unstable if loaded incorrectly, or if designed with the wrong geometry. This offers a gut-sense intuitive example of a Hopf bifurcation in the ordinary world, where stable motion becomes unstable and oscillatory as a parameter is varied. The general theory of how the solution sets of dynamical systems change in response to changes of parameters is called bifurcation theory; the term ''bifurcation'' arises, as the set ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Ordinary Differential Equation
In mathematics, an ordinary differential equation (ODE) is a differential equation (DE) dependent on only a single independent variable (mathematics), variable. As with any other DE, its unknown(s) consists of one (or more) Function (mathematics), function(s) and involves the derivatives of those functions. The term "ordinary" is used in contrast with partial differential equation, ''partial'' differential equations (PDEs) which may be with respect to one independent variable, and, less commonly, in contrast with stochastic differential equations, ''stochastic'' differential equations (SDEs) where the progression is random. Differential equations A linear differential equation is a differential equation that is defined by a linear polynomial in the unknown function and its derivatives, that is an equation of the form :a_0(x)y +a_1(x)y' + a_2(x)y'' +\cdots +a_n(x)y^+b(x)=0, where a_0(x),\ldots,a_n(x) and b(x) are arbitrary differentiable functions that do not need to be linea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Symmetry In Mathematics
Symmetry occurs not only in geometry, but also in other branches of mathematics. Symmetry is a type of invariance: the property that a mathematical object remains unchanged under a set of operations or transformations. Given a structured object ''X'' of any sort, a symmetry is a mapping of the object onto itself which preserves the structure. This can occur in many ways; for example, if ''X'' is a set with no additional structure, a symmetry is a bijective map from the set to itself, giving rise to permutation groups. If the object ''X'' is a set of points in the plane with its metric structure or any other metric space, a symmetry is a bijection of the set to itself which preserves the distance between each pair of points (i.e., an isometry). In general, every kind of structure in mathematics will have its own kind of symmetry, many of which are listed in the given points mentioned above. Symmetry in geometry The types of symmetry considered in basic geometry include ref ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Scheme Of Pitchfork Bifurcation Supercritical
Scheme or schemer may refer to: Arts and entertainment * ''The Scheme'', a BBC Scotland documentary TV series * The Scheme (band), an English pop band * ''The Scheme'', an action role-playing video game for the PC-8801, made by Quest Corporation * Schemer (comics), Richard Fisk, a Marvel Comics villain turned antihero * Horace Schemer, a fictional character in the TV series ''Shining Time Station'' * ''Schemers'' (film), a Scottish film Computing * Scheme (programming language), a minimalist dialect of Lisp * Scheme (URI), the front part of a web link, like "http" or "ftp" * Google Schemer, a former service allowing its users to share plans and interests Other uses * Classification scheme (information science), eg a thesaurus, a taxonomy, a data model or an ontology * Scheme (mathematics), a concept in algebraic geometry * Scheme (rhetoric), a figure of speech that changes a sentence's structure * Scam, an attempt to swindle or cheat people through deception * Scheme, a type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Normal Form (bifurcation Theory)
In mathematics, the normal form of a dynamical system is a simplified form that can be useful in determining the system's behavior. Normal forms are often used for determining local bifurcations in a system. All systems exhibiting a certain type of bifurcation are locally (around the equilibrium) topologically equivalent to the normal form of the bifurcation. For example, the normal form of a saddle-node bifurcation is : \frac = \mu + x^2 where \mu is the bifurcation parameter. The transcritical bifurcation : \frac = r \ln x + x - 1 near x=1 can be converted to the normal form : \frac = R u - u^2 + O(u^3) with the transformation u = \frac(x -1), R = r + 1 .Strogatz, Steven. "Nonlinear Dynamics and Chaos". Westview Press, 2001. p. 52. See also canonical form In mathematics and computer science, a canonical, normal, or standard form of a mathematical object is a standard way of presenting that object as a mathematical expression. Often, it is one which provides ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Scheme Of Pitchfork Bifurcation Subcritical
Scheme or schemer may refer to: Arts and entertainment * ''The Scheme'', a BBC Scotland documentary TV series * The Scheme (band), an English pop band * ''The Scheme'', an action role-playing video game for the PC-8801, made by Quest Corporation * Schemer (comics), Richard Fisk, a Marvel Comics villain turned antihero * Horace Schemer, a fictional character in the TV series ''Shining Time Station'' * ''Schemers'' (film), a Scottish film Computing * Scheme (programming language), a minimalist dialect of Lisp * Scheme (URI), the front part of a web link, like "http" or "ftp" * Google Schemer, a former service allowing its users to share plans and interests Other uses * Classification scheme (information science), eg a thesaurus, a taxonomy, a data model or an ontology * Scheme (mathematics), a concept in algebraic geometry * Scheme (rhetoric), a figure of speech that changes a sentence's structure * Scam, an attempt to swindle or cheat people through deception * Scheme, a type of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Odd Function
In mathematics, an even function is a real function such that f(-x)=f(x) for every x in its domain. Similarly, an odd function is a function such that f(-x)=-f(x) for every x in its domain. They are named for the parity of the powers of the power functions which satisfy each condition: the function f(x) = x^n is even if ''n'' is an even integer, and it is odd if ''n'' is an odd integer. Even functions are those real functions whose graph is self-symmetric with respect to the and odd functions are those whose graph is self-symmetric with respect to the origin. If the domain of a real function is self-symmetric with respect to the origin, then the function can be uniquely decomposed as the sum of an even function and an odd function. Early history The concept of even and odd functions appears to date back to the early 18th century, with Leonard Euler playing a significant role in their formalization. Euler introduced the concepts of even and odd functions (using Lati ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
Bifurcation Theory
Bifurcation theory is the Mathematics, mathematical study of changes in the qualitative or topological structure of a given family of curves, such as the integral curves of a family of vector fields, and the solutions of a family of differential equations. Most commonly applied to the mathematics, mathematical study of dynamical systems, a bifurcation occurs when a small smooth change made to the parameter values (the bifurcation parameters) of a system causes a sudden 'qualitative' or topological change in its behavior. Bifurcations occur in both continuous systems (described by Ordinary differential equation, ordinary, Delay differential equation, delay or Partial differential equation, partial differential equations) and discrete systems (described by maps). The name "bifurcation" was first introduced by Henri Poincaré in 1885 in the first paper in mathematics showing such a behavior. Bifurcation types It is useful to divide bifurcations into two principal classes: * Local bif ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |
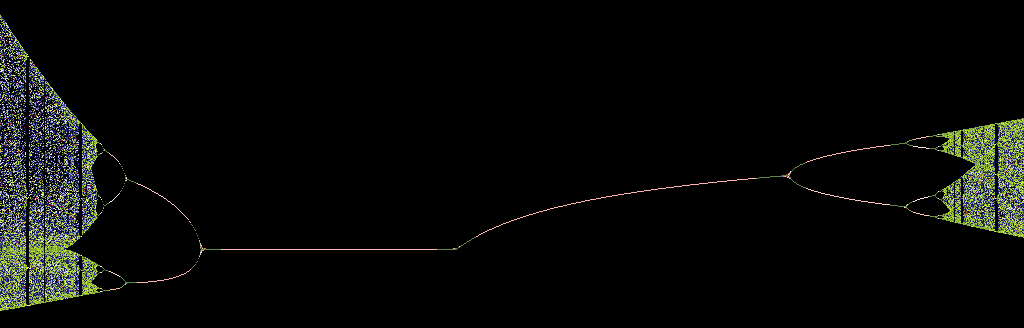
Bifurcation Diagram
In mathematics, particularly in dynamical systems, a bifurcation diagram shows the values visited or approached asymptotically ( fixed points, periodic orbits, or chaotic attractors) of a system as a function of a bifurcation parameter in the system. It is usual to represent stable values with a solid line and unstable values with a dotted line, although often the unstable points are omitted. Bifurcation diagrams enable the visualization of bifurcation theory. In the context of discrete-time dynamical systems, the diagram is also called orbit diagram. Logistic map An example is the bifurcation diagram of the logistic map: x_=rx_n(1-x_n). The bifurcation parameter ''r'' is shown on the horizontal axis of the plot and the vertical axis shows the set of values of the logistic function visited asymptotically from almost all initial conditions. The bifurcation diagram shows the forking of the periods of stable orbits from 1 to 2 to 4 to 8 etc. Each of these bifurcation poi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] [Amazon] |