|
Picking Sequence
A picking sequence is a protocol for fair item assignment. Suppose ''m'' items have to be divided among ''n'' agents. One way to allocate the items is to let one agent select a single item, then let another agent select a single item, and so on. A picking-sequence is a sequence of ''m'' agent-names, where each name determines what agent is the next to pick an item. As an example, suppose 4 items have to be divided between Alice and Bob. Some possible picking sequences are: * AABB - Alice picks two items, then Bob picks the two remaining items. * ABAB - Alice picks one item, then Bob picks one item, then Alice again, then Bob again. This is more "fair" than AABB since it lets Bob more chance to get a better item. * ABBA - Alice picks one item, then Bob picks two items, then Alice receives the remaining item. This is intuitively even more "fair" than ABAB, since, in ABAB, Bob is always behind of Alice, while ABBA is more balanced. Advantages A picking-sequence has several merits as ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Fair Item Assignment
Fair item allocation is a kind of a fair division problem in which the items to divide are ''discrete'' rather than continuous. The items have to be divided among several partners who value them differently, and each item has to be given as a whole to a single person. This situation arises in various real-life scenarios: * Several heirs want to divide the inherited property, which contains e.g. a house, a car, a piano and several paintings. * Several lecturers want to divide the courses given in their faculty. Each lecturer can teach one or more whole courses. * White elephant gift exchange parties The indivisibility of the items implies that a fair division may not be possible. As an extreme example, if there is only a single item (e.g. a house), it must be given to a single partner, but this is not fair to the other partners. This is in contrast to the fair cake-cutting problem, where the dividend is divisible and a fair division always exists. In some cases, the indivisibility ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
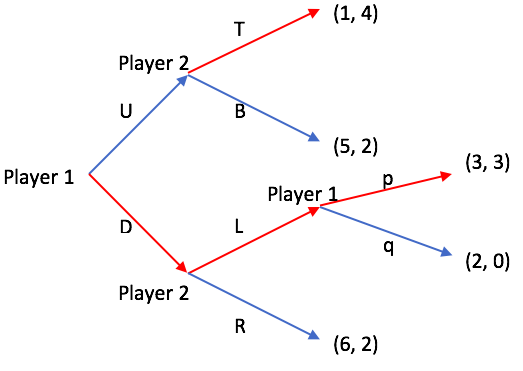
Subgame-perfect Equilibrium
In game theory, a subgame perfect equilibrium (or subgame perfect Nash equilibrium) is a refinement of a Nash equilibrium used in dynamic games. A strategy profile is a subgame perfect equilibrium if it represents a Nash equilibrium of every subgame of the original game. Informally, this means that at any point in the game, the players' behavior from that point onward should represent a Nash equilibrium of the continuation game (i.e. of the subgame), no matter what happened before. Every finite extensive game with perfect recall has a subgame perfect equilibrium. Perfect recall is a term introduced by Harold W. Kuhn in 1953 and ''"equivalent to the assertion that each player is allowed by the rules of the game to remember everything he knew at previous moves and all of his choices at those moves"''. A common method for determining subgame perfect equilibria in the case of a finite game is backward induction. Here one first considers the last actions of the game and determin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Round-robin Item Allocation
Round robin is a procedure for fair item allocation. It can be used to allocate several indivisible items among several people, such that the allocation is "almost" envy-free: each agent believes that the bundle he received is at least as good as the bundle of any other agent, when at most one item is removed from the other bundle. In sports, the round-robin procedure is called a draft. Setting There are ''m'' objects to allocate, and ''n'' people ("agents") with equal rights to these objects. Each person has different preferences over the objects. The preferences of an agent are given by a vector of values - a value for each object. It is assumed that the value of a bundle for an agent is the sum of the values of the objects in the bundle (in other words, the agents' valuations are an additive set function on the set of objects). Description The protocol proceeds as follows: # Number the people arbitrarily from 1 to n; # While there are unassigned objects: #* Let each p ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Competitive Equilibrium
Competitive equilibrium (also called: Walrasian equilibrium) is a concept of economic equilibrium introduced by Kenneth Arrow and Gérard Debreu in 1951 appropriate for the analysis of commodity markets with flexible prices and many traders, and serving as the benchmark of efficiency in economic analysis. It relies crucially on the assumption of a competitive environment where each trader decides upon a quantity that is so small compared to the total quantity traded in the market that their individual transactions have no influence on the prices. Competitive markets are an ideal standard by which other market structures are evaluated. Definitions A competitive equilibrium (CE) consists of two elements: * A price function P. It takes as argument a vector representing a bundle of commodities, and returns a positive real number that represents its price. Usually the price function is linear - it is represented as a vector of prices, a price for each commodity type. * An allocation ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Thomas Jefferson
Thomas Jefferson (April 13, 1743 – July 4, 1826) was an American statesman, diplomat, lawyer, architect, philosopher, and Founding Father who served as the third president of the United States from 1801 to 1809. He was previously the nation's second vice president under John Adams and the first United States secretary of state under George Washington. The principal author of the Declaration of Independence, Jefferson was a proponent of democracy, republicanism, and individual rights, motivating American colonists to break from the Kingdom of Great Britain and form a new nation. He produced formative documents and decisions at state, national, and international levels. During the American Revolution, Jefferson represented Virginia in the Continental Congress that adopted the Declaration of Independence. As a Virginia legislator, he drafted a state law for religious freedom. He served as the second Governor of Virginia from 1779 to 1781, during the Revolutionary War. ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Daniel Webster
Daniel Webster (January 18, 1782 – October 24, 1852) was an American lawyer and statesman who represented New Hampshire and Massachusetts in the U.S. Congress and served as the U.S. Secretary of State under Presidents William Henry Harrison, John Tyler, and Millard Fillmore. Webster was one of the most prominent American lawyers of the 19th century, and argued over 200 cases before the U.S. Supreme Court between 1814 and his death in 1852. During his life, he was a member of the Federalist Party, the National Republican Party, and the Whig Party. Born in New Hampshire in 1782, Webster established a successful legal practice in Portsmouth, New Hampshire, after graduating from Dartmouth College and undergoing a legal apprenticeship. He emerged as a prominent opponent of the War of 1812 and won election to the United States House of Representatives, where he served as a leader of the Federalist Party. Webster left office after two terms and relocated to Boston, Massa ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Apportionment (politics)
Apportionment is the process by which seats in a legislative body are distributed among administrative divisions, such as states or parties, entitled to representation. This page presents the general principles and issues related to apportionment. The page Apportionment by country describes specific practices used around the world. The page Mathematics of apportionment describes mathematical formulations and properties of apportionment rules. The simplest and most universal principle is that elections should give each voter's intentions equal weight. This is both intuitive and stated in laws such as the Fourteenth Amendment to the United States Constitution (the Equal Protection Clause). However, there are a variety of historical and technical reasons why this principle is not followed absolutely or, in some cases, as a first priority. Common problems Fundamentally, the representation of a population in the thousands or millions by a reasonable size, thus accountable gove ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Truthful Mechanism
In game theory, an asymmetric game where players have private information is said to be strategy-proof or strategyproof (SP) if it is a weakly-dominant strategy for every player to reveal his/her private information, i.e. given no information about what the others do, you fare best or at least not worse by being truthful. SP is also called truthful or dominant-strategy-incentive-compatible (DSIC), to distinguish it from other kinds of incentive compatibility. An SP game is not always immune to collusion, but its robust variants are; with group strategyproofness no group of people can collude to misreport their preferences in a way that makes every member better off, and with strong group strategyproofness no group of people can collude to misreport their preferences in a way that makes at least one member of the group better off without making any of the remaining members worse off. Examples Typical examples of SP mechanisms are majority voting between two alternatives, secon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pareto Efficient
Pareto efficiency or Pareto optimality is a situation where no action or allocation is available that makes one individual better off without making another worse off. The concept is named after Vilfredo Pareto (1848–1923), Italian civil engineer and economist, who used the concept in his studies of economic efficiency and income distribution. The following three concepts are closely related: * Given an initial situation, a Pareto improvement is a new situation where some agents will gain, and no agents will lose. * A situation is called Pareto-dominated if there exists a possible Pareto improvement. * A situation is called Pareto-optimal or Pareto-efficient if no change could lead to improved satisfaction for some agent without some other agent losing or, equivalently, if there is no scope for further Pareto improvement. The Pareto front (also called Pareto frontier or Pareto set) is the set of all Pareto-efficient situations. Pareto originally used the word "optimal" for th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sequential Game
In game theory, a sequential game is a game where one player chooses their action before the others choose theirs. The other players must have information on the first player's choice so that the difference in time has no strategic effect. Sequential games are governed by the time axis and represented in the form of decision trees. Sequential games with perfect information can be analysed mathematically using combinatorial game theory. Decision trees are the extensive form of dynamic games that provide information on the possible ways that a given game can be played. They show the sequence in which players act and the number of times that they can each make a decision. Decision trees also provide information on what each player knows or does not know at the point in time they decide on an action to take. Payoffs for each player are given at the decision nodes of the tree. Extensive form representations were introduced by Neumann and further developed by Kuhn in the earliest yea ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Communication Complexity
In theoretical computer science, communication complexity studies the amount of communication required to solve a problem when the input to the problem is distributed among two or more parties. The study of communication complexity was first introduced by Andrew Yao in 1979, while studying the problem of computation distributed among several machines. The problem is usually stated as follows: two parties (traditionally called Alice and Bob) each receive a (potentially different) n-bit string x and y. The ''goal'' is for Alice to compute the value of a certain function, f(x, y), that depends on both x and y, with the least amount of communication between them. While Alice and Bob can always succeed by having Bob send his whole n-bit string to Alice (who then computes the function f), the idea here is to find clever ways of calculating ''f'' with fewer than n bits of communication. Note that, unlike in computational complexity theory, communication complexity is not concerned with th ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Responsive Preferences
In utility theory, the responsive set (RS) extension is an extension of a preference-relation on individual items, to a partial preference-relation of item-bundles. Example Suppose there are four items: w,x,y,z. A person states that he ranks the items according to the following total order: :w \prec x \prec y \prec z (i.e., z is his best item, then y, then x, then w). Assuming the items are independent goods, one can deduce that: :\ \prec \ – the person prefers his two best items to his two worst items; :\ \prec \ – the person prefers his best and third-best items to his second-best and fourth-best items. But, one cannot deduce anything about the bundles \, \; we do not know which of them the person prefers. The RS extension of the ranking w \prec x \prec y \prec z is a partial order on the bundles of items, that includes all relations that can be deduced from the item-ranking and the independence assumption. Definitions Let O be a set of objects and \preceq a total or ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |