|
Period Three Implies Chaos
James A. Yorke (born August 3, 1941) is a Distinguished University Research Professor of Mathematics and Physics and former chair of the Mathematics Department at the University of Maryland, College Park. Born in Plainfield, New Jersey, United States, Yorke attended The Pingry School, then located in Hillside, New Jersey. Yorke is now a Distinguished University Research Professor of Mathematics and Physics with the Institute for Physical Science and Technology at the University of Maryland. In June 2013, Dr. Yorke retired as chair of the University of Maryland's Math department. He devotes his university efforts to collaborative research in chaos theory and genomics. He and Benoit Mandelbrot were the recipients of the 2003 Japan Prize in Science and Technology: Yorke was selected for his work in chaotic systems. In 2003 He was elected a Fellow of the American Physical Society. and in 2012 became a fellow of the American Mathematical Society. He received the Doctor Honoris Caus ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Plainfield, New Jersey
Plainfield is a city in Union County, in the U.S. state of New Jersey, known by its nickname as "The Queen City."About City of Plainfield. Accessed December 29, 2021. "Plainfield Is Nicknamed 'The Queen City.'" The city is both a regional hub for and a of the , located within the core of the [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chaos (mathematics)
Chaos theory is an interdisciplinary area of scientific study and branch of mathematics focused on underlying patterns and deterministic laws of dynamical systems that are highly sensitive to initial conditions, and were once thought to have completely random states of disorder and irregularities. Chaos theory states that within the apparent randomness of chaotic complex systems, there are underlying patterns, interconnection, constant feedback loops, repetition, self-similarity, fractals, and self-organization. The butterfly effect, an underlying principle of chaos, describes how a small change in one state of a deterministic nonlinear system can result in large differences in a later state (meaning that there is sensitive dependence on initial conditions). A metaphor for this behavior is that a butterfly flapping its wings in Brazil can cause a tornado in Texas. Small differences in initial conditions, such as those due to errors in measurements or due to rounding errors i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Kathleen T
Kathleen may refer to: People * Kathleen (given name) * Kathleen (singer), Canadian pop singer Places * Kathleen, Alberta, Canada * Kathleen, Georgia, United States * Kathleen, Florida, United States * Kathleen High School (Lakeland, Florida), United States * Kathleen, Western Australia, Western Australia * Kathleen Island, Tasmania, Australia * Kathleen Lumley College, South Australia * Mary Kathleen, Queensland, former mining settlement in Australia Other * ''Kathleen'' (film), a 1941 American film directed by Harold S. Bucquet * ''The Countess Kathleen and Various Legends and Lyrics'' (1892), second poetry collection of William Butler Yeats * Kathleen Ferrier Award, competition for opera singers * Kathleen Mitchell Award, Australian literature prize for young authors * Plan Kathleen, plan for a German invasion of Northern Ireland sanctioned by the IRA Chief of Staff in 1940 * Tropical Storm Kathleen (other) * "Kathleen" (song), a song by Catfish and the Bottl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Control Of Chaos
In lab experiments that study chaos theory, approaches designed to control chaos are based on certain observed system behaviors. Any chaotic attractor contains an infinite number of unstable, periodic orbits. Chaotic dynamics, then, consists of a motion where the system state moves in the neighborhood of one of these orbits for a while, then falls close to a different unstable, periodic orbit where it remains for a limited time and so forth. This results in a complicated and unpredictable wandering over longer periods of time. Control of chaos is the stabilization, by means of small system perturbations, of one of these unstable periodic orbits. The result is to render an otherwise chaotic motion more stable and predictable, which is often an advantage. The perturbation must be tiny compared to the overall size of the attractor of the system to avoid significant modification of the system's natural dynamics. Several techniques have been devised for chaos control, but most are de ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Celso Grebogi
Celso Grebogi (born 1947) is a Brazilian theoretical physicist who works in the area of chaos theory. He is one among the pioneers in the nonlinear and complex systems and chaos theory. Currently he works at the University of Aberdeen as the "Sixth Century Chair in Nonlinear and Complex Systems". He has done extensive research in the field of plasma physics before his work on the theory of dynamical systems. He and his colleagues (Edward Ott and James A. Yorke) have shown with a numerical example that one can convert a chaotic attractor to any one of numerous possible attracting time-periodic motions by making only small time-dependent perturbations of an available system parameter. This article is considered as one among the classic works in the control theory of chaos and their control method is known as the OGY method. He was listed in the 2016 Thomson Reuters Citation Laureates. Research areas Grebogi has worked in the fields of dynamics of nonlinear and complex systems in ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Edward Ott
Edward Ott (born 22 December 1941) is an American physicist most noted for his contributions to the development of chaos theory. Ott was born and grew up in New York City. He attended Stuyvesant High School, received his bachelor's degree in Electrical Engineering from The Cooper Union, and his Ph.D. in Electrophysics from The Polytechnic Institute of Brooklyn in 1967. Following receipt of his Ph.D. he was an NSF postdoctoral fellow in the Department of Applied Mathematics and Theoretical Physics of Cambridge University. He then joined the faculty of the Department of Electrical Engineering at Cornell University. Since 1979 he has been a faculty member jointly in the Department of Physics and the Department of Electrical Engineering at The University of Maryland, with the current titles of Distinguished University Professor, and Yuen Sang and Yuen Kit So Professor. He was elected to the National Academy of Sciences in 2022. Research areas Prior to his work on chaos and compl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
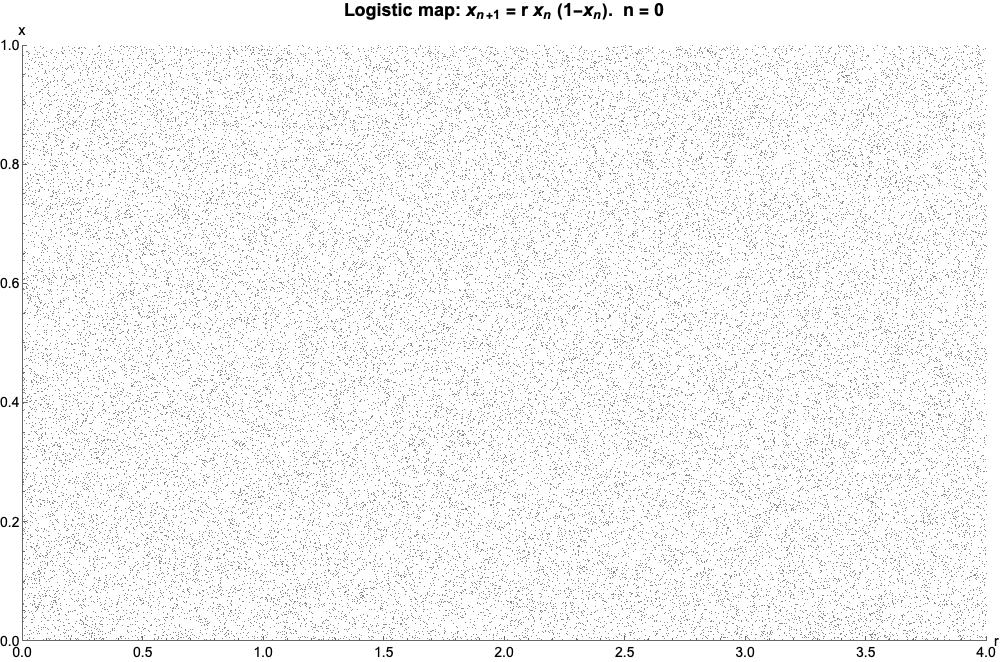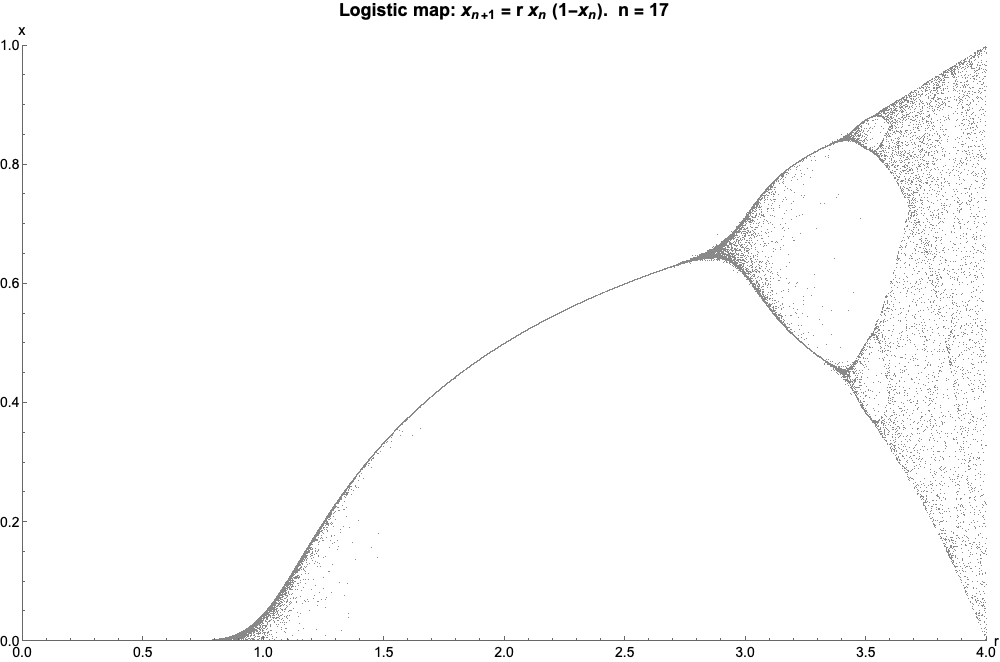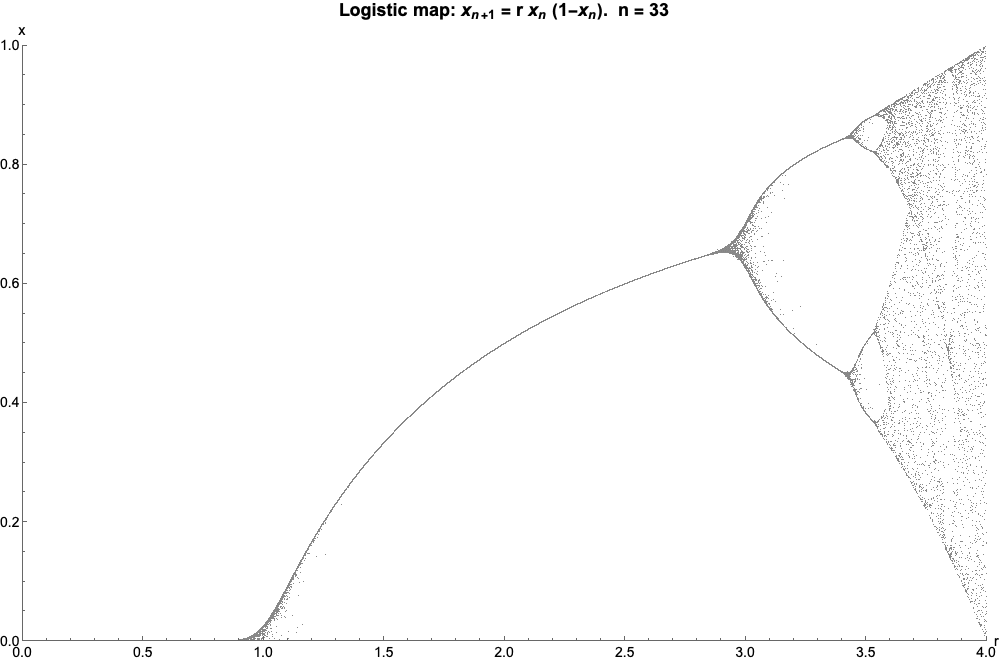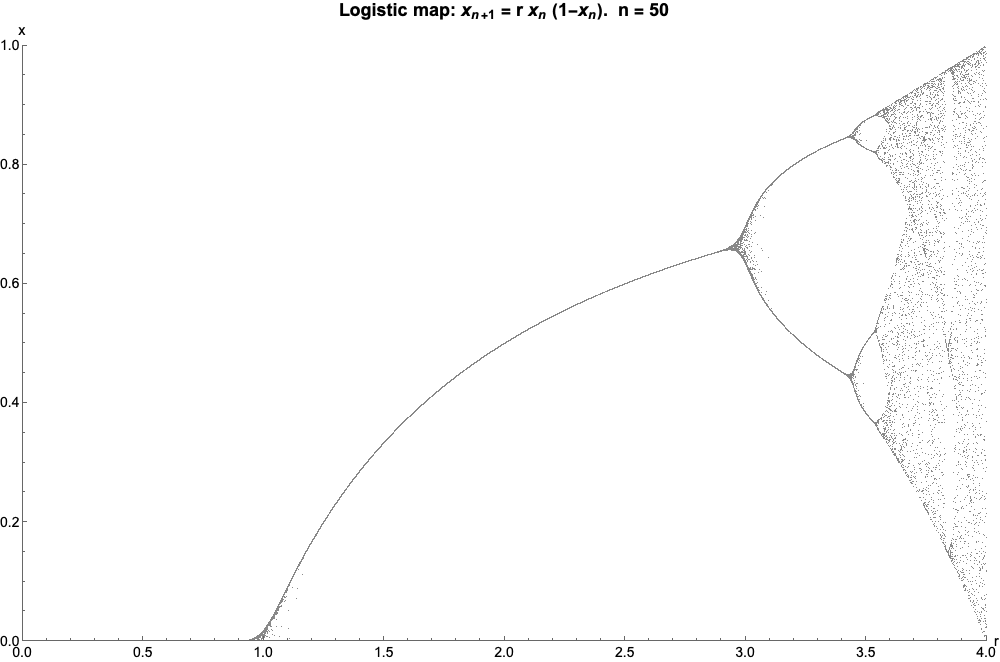
Logistic Map
The logistic map is a polynomial mapping (equivalently, recurrence relation) of degree 2, often referred to as an archetypal example of how complex, chaotic behaviour can arise from very simple non-linear dynamical equations. The map was popularized in a 1976 paper by the biologist Robert May, in part as a discrete-time demographic model analogous to the logistic equation written down by Pierre François Verhulst. Mathematically, the logistic map is written where is a number between zero and one, that represents the ratio of existing population to the maximum possible population. This nonlinear difference equation is intended to capture two effects: * ''reproduction'' where the population will increase at a rate proportional to the current population when the population size is small. * ''starvation'' (density-dependent mortality) where the growth rate will decrease at a rate proportional to the value obtained by taking the theoretical "carrying capacity" of the environment l ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Measure (mathematics)
In mathematics, the concept of a measure is a generalization and formalization of geometrical measures ( length, area, volume) and other common notions, such as mass and probability of events. These seemingly distinct concepts have many similarities and can often be treated together in a single mathematical context. Measures are foundational in probability theory, integration theory, and can be generalized to assume negative values, as with electrical charge. Far-reaching generalizations (such as spectral measures and projection-valued measures) of measure are widely used in quantum physics and physics in general. The intuition behind this concept dates back to ancient Greece, when Archimedes tried to calculate the area of a circle. But it was not until the late 19th and early 20th centuries that measure theory became a branch of mathematics. The foundations of modern measure theory were laid in the works of Émile Borel, Henri Lebesgue, Nikolai Luzin, Johann Radon, Const ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Nonlinearity (journal)
''Nonlinearity'' is a peer-reviewed scientific journal published by IOP Publishing and the London Mathematical Society. The journal publishes papers on nonlinear mathematics, mathematical physics, experimental physics, theoretical physics and other areas in the sciences where nonlinear phenomena are of fundamental importance. The Editors-in-Chief are Tasso J Kaper (Boston University) for IOP Publishing and Konstantin Khanin (University of Toronto) for the London Mathematical Society. Abstracting and indexing The journal is abstracted and indexed in Science Citation Index, Current Contents/Physical, Chemical & Earth Sciences, Inspec, CompuMath Citation Index, Mathematical Reviews, MathSciNet, Zentralblatt MATH, and VINITI Database RAS. According to the ''Journal Citation Reports'', the journal has a 2020 impact factor of 2.129. See also * ''Journal of Physics A'' * ''Inverse Problems'' *London Mathematical Society *IOP Publishing IOP Publishing (previously Institute of Ph ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Journal Für Die Reine Und Angewandte Mathematik
''Crelle's Journal'', or just ''Crelle'', is the common name for a mathematics journal, the ''Journal für die reine und angewandte Mathematik'' (in English: ''Journal for Pure and Applied Mathematics''). History The journal was founded by August Leopold Crelle (Berlin) in 1826 and edited by him until his death in 1855. It was one of the first major mathematical journals that was not a proceedings of an academy. It has published many notable papers, including works of Niels Henrik Abel, Georg Cantor, Gotthold Eisenstein, Carl Friedrich Gauss and Otto Hesse. It was edited by Carl Wilhelm Borchardt from 1856 to 1880, during which time it was known as ''Borchardt's Journal''. The current editor-in-chief is Rainer Weissauer (Ruprecht-Karls-Universität Heidelberg) Past editors * 1826–1856 August Leopold Crelle * 1856–1880 Carl Wilhelm Borchardt * 1881–1888 Leopold Kronecker, Karl Weierstrass * 1889–1892 Leopold Kronecker * 1892–1902 Lazarus Fuchs * 1903–1928 Kurt Hens ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Uncountable Set
In mathematics, an uncountable set (or uncountably infinite set) is an infinite set that contains too many elements to be countable. The uncountability of a set is closely related to its cardinal number: a set is uncountable if its cardinal number is larger than that of the set of all natural numbers. Characterizations There are many equivalent characterizations of uncountability. A set ''X'' is uncountable if and only if any of the following conditions hold: * There is no injective function (hence no bijection) from ''X'' to the set of natural numbers. * ''X'' is nonempty and for every ω-sequence of elements of ''X'', there exists at least one element of X not included in it. That is, ''X'' is nonempty and there is no surjective function from the natural numbers to ''X''. * The cardinality of ''X'' is neither finite nor equal to \aleph_0 (aleph-null, the cardinality of the natural numbers). * The set ''X'' has cardinality strictly greater than \aleph_0. The first three ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
.svg "Click for more on -> Measure (mathematics)")