|
Probit
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables. Mathematically, the probit is the inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96, and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, generating a value of a standard normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probit Plot
In probability theory and statistics, the probit function is the quantile function associated with the standard normal distribution. It has applications in data analysis and machine learning, in particular exploratory statistical graphics and specialized regression modeling of binary response variables. Mathematically, the probit is the inverse of the cumulative distribution function of the standard normal distribution, which is denoted as \Phi(z), so the probit is defined as :\operatorname(p) = \Phi^(p) \quad \text \quad p \in (0,1). Largely because of the central limit theorem, the standard normal distribution plays a fundamental role in probability theory and statistics. If we consider the familiar fact that the standard normal distribution places 95% of probability between −1.96 and 1.96, and is symmetric around zero, it follows that :\Phi(-1.96) = 0.025 = 1-\Phi(1.96).\,\! The probit function gives the 'inverse' computation, generating a value of a standard normal ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Probit Model
In statistics, a probit model is a type of regression where the dependent variable can take only two values, for example married or not married. The word is a portmanteau, coming from ''probability'' + ''unit''. The purpose of the model is to estimate the probability that an observation with particular characteristics will fall into a specific one of the categories; moreover, classifying observations based on their predicted probabilities is a type of binary classification model. A probit model is a popular specification for a binary response model. As such it treats the same set of problems as does logistic regression using similar techniques. When viewed in the generalized linear model framework, the probit model employs a probit link function. It is most often estimated using the maximum likelihood procedure, such an estimation being called a probit regression. Conceptual framework Suppose a response variable ''Y'' is ''binary'', that is it can have only two possible outcomes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimation theory, estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logit Model
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, hence the name. The unit of measurement for the log-odd ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logistic Regression
In statistics, the logistic model (or logit model) is a statistical model that models the probability of an event taking place by having the log-odds for the event be a linear function (calculus), linear combination of one or more independent variables. In regression analysis, logistic regression (or logit regression) is estimation theory, estimating the parameters of a logistic model (the coefficients in the linear combination). Formally, in binary logistic regression there is a single binary variable, binary dependent variable, coded by an indicator variable, where the two values are labeled "0" and "1", while the independent variables can each be a binary variable (two classes, coded by an indicator variable) or a continuous variable (any real value). The corresponding probability of the value labeled "1" can vary between 0 (certainly the value "0") and 1 (certainly the value "1"), hence the labeling; the function that converts log-odds to probability is the logistic function, h ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Logit
In statistics, the logit ( ) function is the quantile function associated with the standard logistic distribution. It has many uses in data analysis and machine learning, especially in data transformations. Mathematically, the logit is the inverse of the standard logistic function \sigma(x) = 1/(1+e^), so the logit is defined as :\operatorname p = \sigma^(p) = \ln \frac \quad \text \quad p \in (0,1). Because of this, the logit is also called the log-odds since it is equal to the logarithm of the odds \frac where is a probability. Thus, the logit is a type of function that maps probability values from (0, 1) to real numbers in (-\infty, +\infty), akin to the probit function. Definition If is a probability, then is the corresponding odds; the of the probability is the logarithm of the odds, i.e.: :\operatorname(p)=\ln\left( \frac \right) =\ln(p)-\ln(1-p)=-\ln\left( \frac-1\right)=2\operatorname(2p-1) The base of the logarithm function used is of little importance in the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Generalized Linear Model
In statistics, a generalized linear model (GLM) is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a ''link function'' and by allowing the magnitude of the variance of each measurement to be a function of its predicted value. Generalized linear models were formulated by John Nelder and Robert Wedderburn as a way of unifying various other statistical models, including linear regression, logistic regression and Poisson regression. They proposed an iteratively reweighted least squares method for maximum likelihood estimation (MLE) of the model parameters. MLE remains popular and is the default method on many statistical computing packages. Other approaches, including Bayesian regression and least squares fitting to variance stabilized responses, have been developed. Intuition Ordinary linear regression predicts the expected value of a given unknown quantity ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
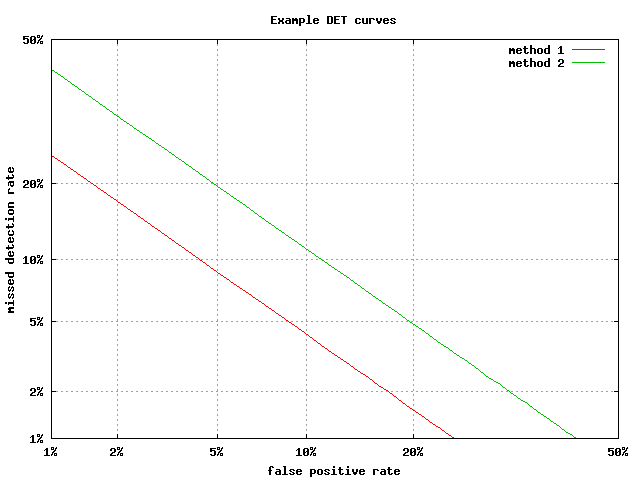
Detection Error Tradeoff
A detection error tradeoff (DET) graph is a graphical plot of error rates for binary classification systems, plotting the false rejection rate vs. false acceptance rate.A. Martin, A., G. Doddington, T. Kamm, M. Ordowski, and M. Przybocki.The DET Curve in Assessment of Detection Task Performance, Proc. Eurospeech '97, Rhodes, Greece, September 1997, Vol. 4, pp. 1895-1898. The x- and y-axes are scaled non-linearly by their standard normal deviates (or just by logarithmic transformation), yielding tradeoff curves that are more linear than ROC curves, and use most of the image area to highlight the differences of importance in the critical operating region. Axis warping The normal deviate mapping (or normal quantile function, or inverse normal cumulative distribution) is given by the probit function, so that the horizontal axis is ''x'' = probit(''Pfa'') and the vertical is ''y'' = probit(''Pfr''), where ''Pfa'' and ''Pfr'' are the false-accept and false-reject rates. The probit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Regression Analysis
In statistical modeling, regression analysis is a set of statistical processes for estimating the relationships between a dependent variable (often called the 'outcome' or 'response' variable, or a 'label' in machine learning parlance) and one or more independent variables (often called 'predictors', 'covariates', 'explanatory variables' or 'features'). The most common form of regression analysis is linear regression, in which one finds the line (or a more complex linear combination) that most closely fits the data according to a specific mathematical criterion. For example, the method of ordinary least squares computes the unique line (or hyperplane) that minimizes the sum of squared differences between the true data and that line (or hyperplane). For specific mathematical reasons (see linear regression), this allows the researcher to estimate the conditional expectation (or population average value) of the dependent variable when the independent variables take on a given ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chester Ittner Bliss
Chester Ittner Bliss (February 1, 1899 – March 14, 1979) was primarily a biologist, who is best known for his contributions to statistics. He was born in Springfield, Ohio in 1899 and died in 1979. He was the first secretary of the International Biometric Society. Academic qualifications *Bachelor of Arts in Entomology from Ohio State University, 1921 *Master of Arts from Columbia University, 1922 *PhD from Columbia University, 1926 Remarkably, his statistical knowledge was largely self-taught and developed according to the problems he wanted to solve (Cochran & Finney 1979). Nevertheless, in 1942 he was elected as a Fellow of the American Statistical Association. Major contributions The idea of the probit function was published by Bliss in a 1934 article in ''Science'' on how to treat data such as the percentage of a pest killed by a pesticide. Bliss proposed transforming the percentage killed into a "probability unit" (or "probit"). Arguably his most important contributio ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Error Function
In mathematics, the error function (also called the Gauss error function), often denoted by , is a complex function of a complex variable defined as: :\operatorname z = \frac\int_0^z e^\,\mathrm dt. This integral is a special (non- elementary) sigmoid function that occurs often in probability, statistics, and partial differential equations. In many of these applications, the function argument is a real number. If the function argument is real, then the function value is also real. In statistics, for non-negative values of , the error function has the following interpretation: for a random variable that is normally distributed with mean 0 and standard deviation , is the probability that falls in the range . Two closely related functions are the complementary error function () defined as :\operatorname z = 1 - \operatorname z, and the imaginary error function () defined as :\operatorname z = -i\operatorname iz, where is the imaginary unit Name The name "error functi ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantile Function
In probability and statistics, the quantile function, associated with a probability distribution of a random variable, specifies the value of the random variable such that the probability of the variable being less than or equal to that value equals the given probability. Intuitively, the quantile function associates with a range at and below a probability input the likelihood that a random variable is realized in that range for some probability distribution. It is also called the percentile function, percent-point function or inverse cumulative distribution function. Definition Strictly monotonic distribution function With reference to a continuous and strictly monotonic cumulative distribution function F_X\colon \mathbb \to ,1/math> of a random variable ''X'', the quantile function Q\colon , 1\to \mathbb returns a threshold value ''x'' below which random draws from the given c.d.f. would fall ''100*p'' percent of the time. In terms of the distribution function ''F'', the q ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
