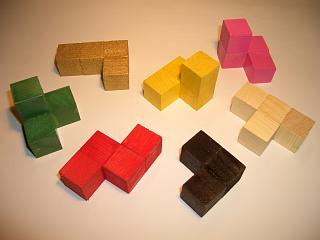|
Polycube
upAll 8 one-sided tetracubes – if chirality is ignored, the bottom 2 in grey are considered the same, giving 7 free tetracubes in total A puzzle involving arranging nine L tricubes into a 3×3 cube A polycube is a solid figure formed by joining one or more equal cubes face to face. Polycubes are the three-dimensional analogues of the planar polyominoes. The Soma cube, the Bedlam cube, the Diabolical cube, the Slothouber–Graatsma puzzle, and the Conway puzzle are examples of packing problems based on polycubes. Enumerating polycubes A chiral pentacube Like polyominoes, polycubes can be enumerated in two ways, depending on whether chiral pairs of polycubes are counted as one polycube or two. For example, 6 tetracubes have mirror symmetry and one is chiral, giving a count of 7 or 8 tetracubes respectively. Unlike polyominoes, polycubes are usually counted with mirror pairs distinguished, because one cannot turn a polycube over to reflect it as one can a polyomino ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Diabolical Cube
The diabolical cube is a three-dimensional dissection puzzle consisting of six polycubes (shapes formed by gluing cubes together face to face) that can be assembled together to form a single 3 × 3 × 3 cube.. The six pieces are: one dicube, one tricube, one tetracube, one pentacube, one hexacube and one heptacube, that is, polycubes of 2, 3, 4, 5, 6 and 7 cubes. There are many similar variations of this type of puzzle, including the Soma cube and the Slothouber–Graatsma puzzle, two other dissections of a 3 × 3 × 3 cube into polycubes which use seven and nine pieces respectively. However, writes that the diabolical cube appears to be the oldest puzzle of this type, first appearing in an 1893 book ''Puzzles Old and New'' by Professor Hoffmann Professor Hoffmann (1839–1919) was the pseudonym of Angelo John Lewis, an English-born barrister and writer who has been described as "the most prolific and influential magic author and transl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling. Polyominoes have been used in popular puzzles since at least 1907, and the enumeration of pentominoes is dated to antiquity. Many results with the pieces of 1 to 6 squares were first published in '' Fairy Chess Review'' between the years 1937 to 1957, under the name of "dissection problems." The name ''polyomino'' was invented by Solomon W. Golomb in 1953, and it was popularized by Martin Gardner in a November 1960 "Mathematical Games" column in ''Scientific American''. Related to polyominoes are polyiamonds, formed from equilateral triangles; polyhexes, formed from regular hexagons; and other plane polyforms. Polyominoes have been generalized to higher dimensions by joining cubes to form polycubes, or hypercubes to form polyhypercubes. In statistical physics, the ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Soma Cube
The Soma cube is a solid dissection puzzle invented by Danish polymath Piet Hein in 1933 during a lecture on quantum mechanics conducted by Werner Heisenberg. Seven pieces made out of unit cubes must be assembled into a 3×3×3 cube. The pieces can also be used to make a variety of other 3D shapes. The pieces of the Soma cube consist of all possible combinations of three or four unit cubes, joined at their faces, such that at least one inside corner is formed. There is one combination of three cubes that satisfies this condition, and six combinations of four cubes that satisfy this condition, of which two are mirror images of each other (see Chirality). Thus, 3 + (6 × 4) is 27, which is exactly the number of cells in a 3×3×3 cube. The Soma cube was popularized by Martin Gardner in the September 1958 Mathematical Games column in ''Scientific American.'' The book '' Winning Ways for your Mathematical Plays'' also contains a detailed analysis of the Soma cube problem. The ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Tesseract
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book '' A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pentomino
Derived from the Greek word for ' 5', and "domino", a pentomino (or 5-omino) is a polyomino of order 5, that is, a polygon in the plane made of 5 equal-sized squares connected edge-to-edge. When rotations and reflections are not considered to be distinct shapes, there are 12 different ''free'' pentominoes. When reflections are considered distinct, there are 18 '' one-sided'' pentominoes. When rotations are also considered distinct, there are 63 '' fixed'' pentominoes. Pentomino tiling puzzles and games are popular in recreational mathematics. Usually, video games such as '' Tetris'' imitations and ''Rampart'' consider mirror reflections to be distinct, and thus use the full set of 18 one-sided pentominoes. Each of the twelve pentominoes satisfies the Conway criterion; hence every pentomino is capable of tiling the plane. Each chiral pentomino can tile the plane without being reflected. History The earliest puzzle containing a complete set of pentominoes appeared in H ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
8-cell Net
In geometry, a tesseract is the four-dimensional analogue of the cube; the tesseract is to the cube as the cube is to the square. Just as the surface of the cube consists of six square faces, the hypersurface of the tesseract consists of eight cubical cells. The tesseract is one of the six convex regular 4-polytopes. The tesseract is also called an 8-cell, C8, (regular) octachoron, octahedroid, cubic prism, and tetracube. It is the four-dimensional hypercube, or 4-cube as a member of the dimensional family of hypercubes or measure polytopes. Coxeter labels it the \gamma_4 polytope. The term ''hypercube'' without a dimension reference is frequently treated as a synonym for this specific polytope. The ''Oxford English Dictionary'' traces the word ''tesseract'' to Charles Howard Hinton's 1888 book ''A New Era of Thought''. The term derives from the Greek ( 'four') and from ( 'ray'), referring to the four edges from each vertex to other vertices. Hinton originally spelled ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Slothouber–Graatsma Puzzle
The Slothouber–Graatsma puzzle is a packing problem that calls for packing six 1 × 2 × 2 blocks and three 1 × 1 × 1 blocks into a 3 × 3 × 3 box. The solution to this puzzle is unique (up to mirror reflections and rotations). It was named after its inventors Jan Slothouber and William Graatsma. The puzzle is essentially the same if the three 1 × 1 × 1 blocks are left out, so that the task is to pack six 1 × 2 × 2 blocks into a cubic box with volume 27. Solution The solution of the Slothouber–Graatsma puzzle is straightforward when one realizes that the three 1 × 1 × 1 blocks (or the three holes) need to be placed along a body diagonal of the box, as each of the 3 x 3 layers in the various directions needs to contain such a unit block. This follows from parity considerations, because the larger blocks can only fill an even number of the 9 cells in each 3 x 3 layer.Elwyn R. Berlekamp, John H. Conway and Richard K. Guy: Winning ways for your mathematical plays, 2nd e ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Bedlam Cube
The Bedlam cube is a solid dissection puzzle invented by British puzzle expert Bruce Bedlam. Design The puzzle consists of thirteen polycubic pieces: twelve pentacubes and one tetracube. The objective is to assemble these pieces into a 4 x 4 x 4 cube. There are 19,186 distinct ways of doing so, up to rotations and reflections. The Bedlam cube is one unit per side larger than the 3 x 3 x 3 Soma cube, and is much more difficult to solve. History Two of the BBC's 'Dragons' from ''Dragons' Den'', Rachel Elnaugh and Theo Paphitis, were to invest in the Bedlam cube during the 2005 series. They offered £100,000 for a 30% share of equity in Bedlam Puzzles. Danny Bamping (the entrepreneur behind Bedlam cube) finally chose a bank loan instead of their investment, as seen in the relevant "Where Are They Now" episode of ''Dragons' Den''. Records According to ''Guinness World Records'', the official world record for assembling the Bedlam Cube is 11.03 seconds by Danny Bamping ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Hexomino
A hexomino (or 6-omino) is a polyomino of order 6, that is, a polygon in the plane made of 6 equal-sized squares connected edge-to-edge. The name of this type of figure is formed with the prefix hex(a)-. When rotations and reflections are not considered to be distinct shapes, there are 35 different ''free'' hexominoes. When reflections are considered distinct, there are 60 ''one-sided'' hexominoes. When rotations are also considered distinct, there are 216 ''fixed'' hexominoes. Symmetry The figure above shows all 35 possible free hexominoes, coloured according to their symmetry groups: * The twenty grey hexominoes have no symmetry. Their symmetry group consists only of the identity mapping. * The six red hexominoes have an axis of mirror symmetry parallel to the gridlines. Their symmetry group has two elements, the identity and a reflection in a line parallel to the sides of the squares. * The two green hexominoes have an axis of mirror symmetry at 45° to the gridlin ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Martin Gardner
Martin Gardner (October 21, 1914May 22, 2010) was an American popular mathematics and popular science writer with interests also encompassing scientific skepticism, micromagic, philosophy, religion, and literatureespecially the writings of Lewis Carroll, L. Frank Baum, and G. K. Chesterton.Martin (2010) He was also a leading authority on Lewis Carroll. '' The Annotated Alice'', which incorporated the text of Carroll's two Alice books, was his most successful work and sold over a million copies. He had a lifelong interest in magic and illusion and in 1999, MAGIC magazine named him as one of the "100 Most Influential Magicians of the Twentieth Century". He was considered the doyen of American puzzlers. He was a prolific and versatile author, publishing more than 100 books. Gardner was best known for creating and sustaining interest in recreational mathematicsand by extension, mathematics in generalthroughout the latter half of the 20th century, principally through his " ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Honeycomb (geometry)
In geometry, a honeycomb is a ''space filling'' or '' close packing'' of polyhedral or higher-dimensional ''cells'', so that there are no gaps. It is an example of the more general mathematical ''tiling'' or ''tessellation'' in any number of dimensions. Its dimension can be clarified as ''n''-honeycomb for a honeycomb of ''n''-dimensional space. Honeycombs are usually constructed in ordinary Euclidean ("flat") space. They may also be constructed in non-Euclidean spaces, such as hyperbolic honeycombs. Any finite uniform polytope can be projected to its circumsphere to form a uniform honeycomb in spherical space. Classification There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered. The simplest honeycombs to build are formed from stacked layers or ''slabs'' of prisms based on some tessellations of the plane. In particu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |