|
Orbital Overlap
In chemical bonds, an orbital overlap is the concentration of orbitals on adjacent atoms in the same regions of space. Orbital overlap can lead to bond formation. Linus Pauling explained the importance of orbital overlap in the molecular bond angles observed through experimentation; it is the basis for orbital hybridization. As ''s'' orbitals are spherical (and have no directionality) and ''p'' orbitals are oriented 90° to each other, a theory was needed to explain why molecules such as methane (CH4) had observed bond angles of 109.5°. Pauling proposed that s and p orbitals on the carbon atom can combine to form hybrids (sp3 in the case of methane) which are directed toward the hydrogen atoms. The carbon hybrid orbitals have greater overlap with the hydrogen orbitals, and can therefore form stronger C–H bonds.Pauling, Linus. (1960). ''The Nature Of The Chemical Bond''. Cornell University Press. A quantitative measure of the overlap of two atomic orbitals ΨA and ΨB o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bond
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force and hydrogen bonding. Strong chemical bonding arises from the sharing or transfer of electrons between the participating atoms. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. An electron positioned between two nuclei will be attracted to both of them, and the nuclei will be attracted toward electrons in this position. This attraction constitu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Molecular Geometry
Molecular geometry is the three-dimensional arrangement of the atoms that constitute a molecule. It includes the general shape of the molecule as well as bond lengths, bond angles, torsional angles and any other geometrical parameters that determine the position of each atom. Molecular geometry influences several properties of a substance including its reactivity, polarity, phase of matter, color, magnetism and biological activity. The angles between bonds that an atom forms depend only weakly on the rest of molecule, i.e. they can be understood as approximately local and hence transferable properties. Determination The molecular geometry can be determined by various spectroscopic methods and diffraction methods. IR, microwave and Raman spectroscopy can give information about the molecule geometry from the details of the vibrational and rotational absorbance detected by these techniques. X-ray crystallography, neutron diffraction and electron diffraction can give molecular ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bonding
A chemical bond is a lasting attraction between atoms or ions that enables the formation of molecules and crystals. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds, or through the sharing of electrons as in covalent bonds. The strength of chemical bonds varies considerably; there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force and hydrogen bonding. Strong chemical bonding arises from the sharing or transfer of electrons between the participating atoms. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. An electron positioned between two nuclei will be attracted to both of them, and the nuclei will be attracted toward electrons in this position. This attraction constitutes ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrices
Matrix most commonly refers to: * ''The Matrix'' (franchise), an American media franchise ** ''The Matrix'', a 1999 science-fiction action film ** "The Matrix", a fictional setting, a virtual reality environment, within ''The Matrix'' (franchise) * Matrix (mathematics), a rectangular array of numbers, symbols or expressions Matrix (or its plural form matrices) may also refer to: Science and mathematics * Matrix (mathematics), algebraic structure, extension of vector into 2 dimensions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Arts and entertainment Fictional entities * Matrix (comics), two comic book ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained. Common metho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sigma Bond
In chemistry, sigma bonds (σ bonds) are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals. Sigma bonding is most simply defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is symmetrical with respect to rotation about the bond axis. By this definition, common forms of sigma bonds are s+s, pz+pz, s+pz and dz2+dz2 (where z is defined as the axis of the bond or the internuclear axis). Quantum theory also indicates that molecular orbitals (MO) of identical symmetry actually mix or ''hybridize''. As a practical consequence of this mixing of diatomic molecules, the wavefunctions s+s and pz+pz molecular orbitals become blended. The extent of this mixing (or hybridization or blending) depends on the relative energies of the MOs of like symmetry. For homodiatomics (homonuclear diatomic molecules), bonding σ orbitals have no nodal planes at which the wavefunction i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pi Bond
In chemistry, pi bonds (π bonds) are covalent chemical bonds, in each of which two lobes of an orbital on one atom overlap with two lobes of an orbital on another atom, and in which this overlap occurs laterally. Each of these atomic orbitals has an electron density of zero at a shared nodal plane that passes through the two bonded nuclei. This plane also is a nodal plane for the molecular orbital of the pi bond. Pi bonds can form in double and triple bonds but do not form in single bonds in most cases. The Greek letter π in their name refers to p orbitals, since the orbital symmetry of the pi bond is the same as that of the p orbital when seen down the bond axis. One common form of this sort of bonding involves p orbitals themselves, though d orbitals also engage in pi bonding. This latter mode forms part of the basis for metal-metal multiple bonding. Pi bonds are usually weaker than sigma bonds. The C-C double bond, composed of one sigma and one pi bond, has a bon ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
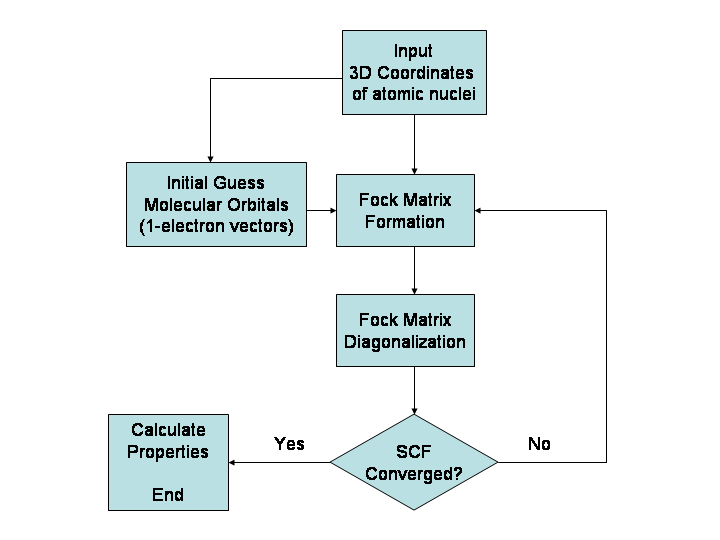
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Especially in the older literature, the Hartree–Fock method is also called the self-consistent field method (SCF). In deriving what is now called the Hartree equation as an approximate solution of the Schrödinger equation, Hartree required the final field as computed from the charge distribution to be "s ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roothaan Equations
The Roothaan equations are a representation of the Hartree–Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally called Restricted Hartree–Fock theory. The method was developed independently by Clemens C. J. Roothaan and George G. Hall in 1951, and is thus sometimes called the ''Roothaan-Hall equations''. The Roothaan equations can be written in a form resembling generalized eigenvalue problem, although they are not a standard eigenvalue problem because they are nonlinear: :\mathbf \mathbf = \mathbf \mathbf \mathbf where F is the Fock matrix (which depends on the coefficients C due to electron-electron interactions), C is a matrix of coefficients, S is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. In the case of an ortho ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number z^\textsfMz is positive for every nonzero real column vector z, where z^\textsf is the transpose of More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number z^* Mz is positive for every nonzero complex column vector z, where z^* denotes the conjugate transpose of z. Positive semi-definite matrices are defined similarly, except that the scalars z^\textsfMz and z^* Mz are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called indefinite. A matrix is thus positive-definite if and only if it is the matrix of a positive-definite quadratic form or Hermitian form. In other words, a matrix is positive-definite if and only if it defines a ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
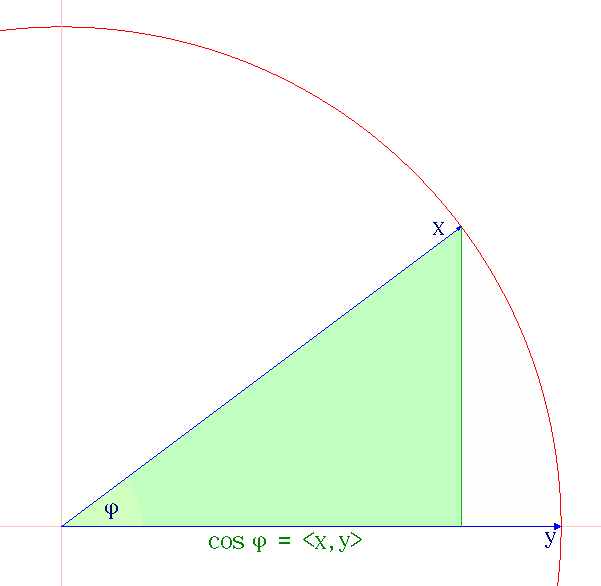
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is considered one of the most important and widely used inequalities in mathematics. The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space it is true that where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every inner product gives rise to a norm, called the or , where the norm of a vector \mathbf is denoted and defined by: \, \mathbf\, := \sqrt so that this norm and the inner product are related by the defining condition \, \mathbf\, ^2 = \langle \mathbf, \mathbf \rangle, where \langle \mathbf, \mathbf \rangle is always a non-negative ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |