|
Overlap Matrix
In chemical bonds, an orbital overlap is the concentration of orbitals on adjacent atoms in the same regions of space. Orbital overlap can lead to bond formation. The general principle for orbital overlap is that, the greater the overlap between orbitals, the greater the bond strength. Linus Pauling explained the importance of orbital overlap in the molecular bond angles observed through experimentation; it is the basis for orbital hybridization. As ''s'' orbitals are spherical (and have no directionality) and ''p'' orbitals are oriented 90° to each other, a theory was needed to explain why molecules such as methane (CH4) had observed bond angles of 109.5°. Pauling proposed that s and p orbitals on the carbon atom can combine to form hybrids (sp3 in the case of methane) which are directed toward the hydrogen atoms. The carbon hybrid orbitals have greater overlap with the hydrogen orbitals, and can therefore form stronger C–H bonds.Pauling, Linus. (1960). ''The Nature ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bond
A chemical bond is the association of atoms or ions to form molecules, crystals, and other structures. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds or through the sharing of electrons as in covalent bonds, or some combination of these effects. Chemical bonds are described as having different strengths: there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force, and hydrogen bonding. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. Electrons shared between two nuclei will be attracted to both of them. "Constructive quantum mechanical wavefunction interference" stabilizes the paired nuclei (see Theories of chemical bonding). Bonded nuclei maintain an optima ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Gramian Matrix
In linear algebra, the Gram matrix (or Gramian matrix, Gramian) of a set of vectors v_1,\dots, v_n in an inner product space is the Hermitian matrix of inner products, whose entries are given by the inner product G_ = \left\langle v_i, v_j \right\rangle., p.441, Theorem 7.2.10 If the vectors v_1,\dots, v_n are the columns of matrix X then the Gram matrix is X^\dagger X in the general case that the vector coordinates are complex numbers, which simplifies to X^\top X for the case that the vector coordinates are real numbers. An important application is to compute linear independence: a set of vectors are linearly independent if and only if the Gram determinant (the determinant of the Gram matrix) is non-zero. It is named after Jørgen Pedersen Gram. Examples For finite-dimensional real vectors in \mathbb^n with the usual Euclidean dot product, the Gram matrix is G = V^\top V, where V is a matrix whose columns are the vectors v_k and V^\top is its transpose whose rows are the vect ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Chemical Bonding
A chemical bond is the association of atoms or ions to form molecules, crystals, and other structures. The bond may result from the electrostatic force between oppositely charged ions as in ionic bonds or through the sharing of electrons as in covalent bonds, or some combination of these effects. Chemical bonds are described as having different strengths: there are "strong bonds" or "primary bonds" such as covalent, ionic and metallic bonds, and "weak bonds" or "secondary bonds" such as dipole–dipole interactions, the London dispersion force, and hydrogen bonding. Since opposite electric charges attract, the negatively charged electrons surrounding the nucleus and the positively charged protons within a nucleus attract each other. Electrons shared between two nuclei will be attracted to both of them. "Constructive quantum mechanical wavefunction interference" stabilizes the paired nuclei (see Theories of chemical bonding). Bonded nuclei maintain an optimal distance (t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Matrices (mathematics)
Matrix (: matrices or matrixes) or MATRIX may refer to: Science and mathematics * Matrix (mathematics), a rectangular array of numbers, symbols or expressions * Matrix (logic), part of a formula in prenex normal form * Matrix (biology), the material in between a eukaryotic organism's cells * Matrix (chemical analysis), the non-analyte components of a sample * Matrix (geology), the fine-grained material in which larger objects are embedded * Matrix (composite), the constituent of a composite material * Hair matrix, produces hair * Nail matrix, part of the nail in anatomy Technology * Matrix (mass spectrometry), a compound that promotes the formation of ions * Matrix (numismatics), a tool used in coin manufacturing * Matrix (printing), a mould for casting letters * Matrix (protocol), an open standard for real-time communication * Matrix (record production), or master, a disc used in the production of phonograph records ** Matrix number, of a gramophone record * D ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Quantum Chemistry
Quantum chemistry, also called molecular quantum mechanics, is a branch of physical chemistry focused on the application of quantum mechanics to chemical systems, particularly towards the quantum-mechanical calculation of electronic contributions to physical and chemical properties of Molecule, molecules, Material, materials, and solutions at the atomic level. These calculations include systematically applied approximations intended to make calculations computationally feasible while still capturing as much information about important contributions to the computed Wave function, wave functions as well as to observable properties such as structures, spectra, and Thermodynamics, thermodynamic properties. Quantum chemistry is also concerned with the computation of quantum effects on molecular dynamics and chemical kinetics. Chemists rely heavily on spectroscopy through which information regarding the Quantization (physics), quantization of energy on a molecular scale can be obtained ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Sigma Bond
In chemistry, sigma bonds (σ bonds) or sigma overlap are the strongest type of covalent chemical bond. They are formed by head-on overlapping between atomic orbitals along the internuclear axis. Sigma bonding is most simply defined for diatomic molecules using the language and tools of symmetry groups. In this formal approach, a σ-bond is symmetrical with respect to rotation about the bond axis. By this definition, common forms of sigma bonds are s+s, pz+pz, s+pz and dz2+dz2 (where z is defined as the axis of the bond or the internuclear axis). Quantum theory also indicates that molecular orbitals (MO) of identical symmetry actually mix or ''hybridize''. As a practical consequence of this mixing of diatomic molecules, the wavefunctions s+s and pz+pz molecular orbitals become blended. The extent of this mixing (or hybridization or blending) depends on the relative energies of the MOs of like symmetry. For homodiatomics ( homonuclear diatomic molecules), bonding σ orbit ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Pi Bond
In chemistry, pi bonds (π bonds) are covalent chemical bonds, in each of which two lobes of an orbital on one atom overlap with two lobes of an orbital on another atom, and in which this overlap occurs laterally. Each of these atomic orbitals has an electron density of zero at a shared nodal plane that passes through the two bonded nuclei. This plane also is a nodal plane for the molecular orbital of the pi bond. Pi bonds can form in double and triple bonds but do not form in single bonds in most cases. The Greek letter π in their name refers to p orbitals, since the orbital symmetry of the pi bond is the same as that of the p orbital when seen down the bond axis. One common form of this sort of bonding involves p orbitals themselves, though d orbitals also engage in pi bonding. This latter mode forms part of the basis for metal-metal multiple bonding. Properties Pi bonds are usually weaker than sigma bonds. The C–C double bond, composed of one sigma and o ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
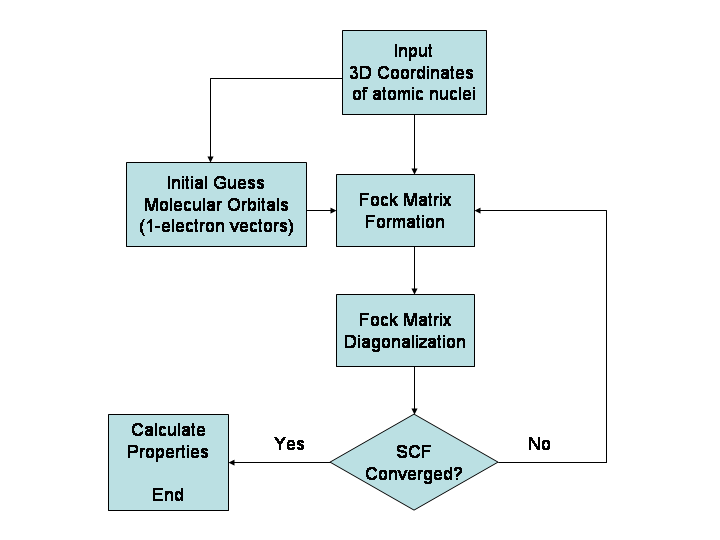
Hartree–Fock Method
In computational physics and chemistry, the Hartree–Fock (HF) method is a method of approximation for the determination of the wave function and the energy of a quantum many-body system in a stationary state. The method is named after Douglas Hartree and Vladimir Fock. The Hartree–Fock method often assumes that the exact ''N''-body wave function of the system can be approximated by a single Slater determinant (in the case where the particles are fermions) or by a single permanent (in the case of bosons) of ''N'' spin-orbitals. By invoking the variational method, one can derive a set of ''N''-coupled equations for the ''N'' spin orbitals. A solution of these equations yields the Hartree–Fock wave function and energy of the system. Hartree–Fock approximation is an instance of mean-field theory, where neglecting higher-order fluctuations in order parameter allows interaction terms to be replaced with quadratic terms, obtaining exactly solvable Hamiltonians. Especially ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Roothaan Equations
The Roothaan equations are a representation of the Hartree–Fock equation in a non orthonormal basis set which can be of Gaussian-type or Slater-type. It applies to closed-shell molecules or atoms where all molecular orbitals or atomic orbitals, respectively, are doubly occupied. This is generally called Restricted Hartree–Fock theory. The method was developed independently by Clemens C. J. Roothaan and George G. Hall in 1951, and is thus sometimes called the ''Roothaan-Hall equations''. The Roothaan equations can be written in a form resembling generalized eigenvalue problem, although they are not a standard eigenvalue problem because they are nonlinear: :\mathbf \mathbf = \mathbf \mathbf \mathbf where F is the Fock matrix (which depends on the coefficients C due to electron-electron interactions), C is a matrix of coefficients, S is the overlap matrix of the basis functions, and \epsilon is the (diagonal, by convention) matrix of orbital energies. In the case of an orth ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Positive-definite Matrix
In mathematics, a symmetric matrix M with real entries is positive-definite if the real number \mathbf^\mathsf M \mathbf is positive for every nonzero real column vector \mathbf, where \mathbf^\mathsf is the row vector transpose of \mathbf. More generally, a Hermitian matrix (that is, a complex matrix equal to its conjugate transpose) is positive-definite if the real number \mathbf^* M \mathbf is positive for every nonzero complex column vector \mathbf, where \mathbf^* denotes the conjugate transpose of \mathbf. Positive semi-definite matrices are defined similarly, except that the scalars \mathbf^\mathsf M \mathbf and \mathbf^* M \mathbf are required to be positive ''or zero'' (that is, nonnegative). Negative-definite and negative semi-definite matrices are defined analogously. A matrix that is not positive semi-definite and not negative semi-definite is sometimes called ''indefinite''. Some authors use more general definitions of definiteness, permitting the matrices to be ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Cauchy–Schwarz Inequality
The Cauchy–Schwarz inequality (also called Cauchy–Bunyakovsky–Schwarz inequality) is an upper bound on the absolute value of the inner product between two vectors in an inner product space in terms of the product of the vector norms. It is considered one of the most important and widely used inequalities in mathematics. Inner products of vectors can describe finite sums (via finite-dimensional vector spaces), infinite series (via vectors in sequence spaces), and integrals (via vectors in Hilbert spaces). The inequality for sums was published by . The corresponding inequality for integrals was published by and . Schwarz gave the modern proof of the integral version. Statement of the inequality The Cauchy–Schwarz inequality states that for all vectors \mathbf and \mathbf of an inner product space where \langle \cdot, \cdot \rangle is the inner product. Examples of inner products include the real and complex dot product; see the examples in inner product. Every ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Off-diagonal Element
In linear algebra, a diagonal matrix is a matrix in which the entries outside the main diagonal are all zero; the term usually refers to square matrices. Elements of the main diagonal can either be zero or nonzero. An example of a 2×2 diagonal matrix is \left begin 3 & 0 \\ 0 & 2 \end\right/math>, while an example of a 3×3 diagonal matrix is \left begin 6 & 0 & 0 \\ 0 & 5 & 0 \\ 0 & 0 & 4 \end\right/math>. An identity matrix of any size, or any multiple of it is a diagonal matrix called a ''scalar matrix'', for example, \left begin 0.5 & 0 \\ 0 & 0.5 \end\right/math>. In geometry, a diagonal matrix may be used as a '' scaling matrix'', since matrix multiplication with it results in changing scale (size) and possibly also shape; only a scalar matrix results in uniform change in scale. Definition As stated above, a diagonal matrix is a matrix in which all off-diagonal entries are zero. That is, the matrix with columns and rows is diagonal if \forall i,j \in \, i \ne j \im ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |