|
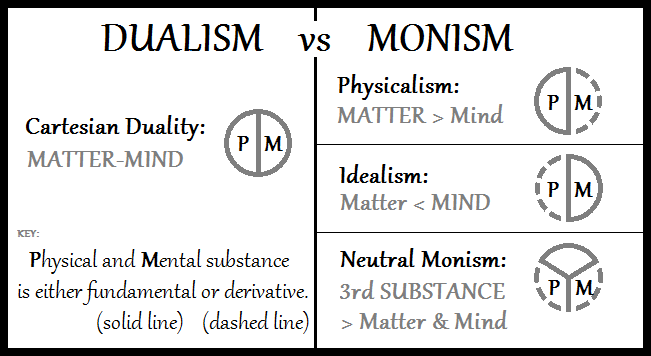
Non-wellfounded Mereology
In philosophy, specifically metaphysics, mereology is the study of parthood relationships. In mathematics and formal logic, wellfoundedness prohibits \cdots |
Philosophy
Philosophy (from , ) is the systematized study of general and fundamental questions, such as those about existence, reason, knowledge, values, mind, and language. Such questions are often posed as problems to be studied or resolved. Some sources claim the term was coined by Pythagoras ( BCE), although this theory is disputed by some. Philosophical methods include questioning, critical discussion, rational argument, and systematic presentation. in . Historically, ''philosophy'' encompassed all bodies of knowledge and a practitioner was known as a ''philosopher''."The English word "philosophy" is first attested to , meaning "knowledge, body of knowledge." "natural philosophy," which began as a discipline in ancient India and Ancient Greece, encompasses astronomy, medicine, and physics. For example, Newton's 1687 ''Mathematical Principles of Natural Philosophy'' later became classified as a book of physics. In the 19th century, the growth of modern research universiti ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Metaphysics
Metaphysics is the branch of philosophy that studies the fundamental nature of reality, the first principles of being, identity and change, space and time, causality, necessity, and possibility. It includes questions about the nature of consciousness and the relationship between mind and matter, between substance and attribute, and between potentiality and actuality. The word "metaphysics" comes from two Greek words that, together, literally mean "after or behind or among he study ofthe natural". It has been suggested that the term might have been coined by a first century CE editor who assembled various small selections of Aristotle's works into the treatise we now know by the name ''Metaphysics'' (μετὰ τὰ φυσικά, ''meta ta physika'', 'after the ''Physics'' ', another of Aristotle's works). Metaphysics studies questions related to what it is for something to exist and what types of existence there are. Metaphysics seeks to answer, in an abstract and fu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mereology
In logic, philosophy and related fields, mereology ( (root: , ''mere-'', 'part') and the suffix ''-logy'', 'study, discussion, science') is the study of parts and the wholes they form. Whereas set theory is founded on the membership relation between a set and its elements, mereology emphasizes the meronomic relation between entities, which—from a set-theoretic perspective—is closer to the concept of inclusion between sets. Mereology has been explored in various ways as applications of predicate logic to formal ontology, in each of which mereology is an important part. Each of these fields provides its own axiomatic definition of mereology. A common element of such axiomatizations is the assumption, shared with inclusion, that the part-whole relation orders its universe, meaning that everything is a part of itself ( reflexivity), that a part of a part of a whole is itself a part of that whole ( transitivity), and that two distinct entities cannot each be a part of the othe ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Mathematics
Mathematics is an area of knowledge that includes the topics of numbers, formulas and related structures, shapes and the spaces in which they are contained, and quantities and their changes. These topics are represented in modern mathematics with the major subdisciplines of number theory, algebra, geometry, and analysis, respectively. There is no general consensus among mathematicians about a common definition for their academic discipline. Most mathematical activity involves the discovery of properties of abstract objects and the use of pure reason to prove them. These objects consist of either abstractions from nature orin modern mathematicsentities that are stipulated to have certain properties, called axioms. A ''proof'' consists of a succession of applications of deductive rules to already established results. These results include previously proved theorems, axioms, andin case of abstraction from naturesome basic properties that are considered true starting points of ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Formal Logic
Logic is the study of correct reasoning. It includes both formal and informal logic. Formal logic is the science of deductively valid inferences or of logical truths. It is a formal science investigating how conclusions follow from premises in a topic-neutral way. When used as a countable noun, the term "a logic" refers to a logical formal system that articulates a proof system. Formal logic contrasts with informal logic, which is associated with informal fallacies, critical thinking, and argumentation theory. While there is no general agreement on how formal and informal logic are to be distinguished, one prominent approach associates their difference with whether the studied arguments are expressed in formal or informal languages. Logic plays a central role in multiple fields, such as philosophy, mathematics, computer science, and linguistics. Logic studies arguments, which consist of a set of premises together with a conclusion. Premises and conclusions are usually under ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Wellfoundedness
In mathematics, a binary relation ''R'' is called well-founded (or wellfounded) on a class ''X'' if every non-empty subset ''S'' ⊆ ''X'' has a minimal element with respect to ''R'', that is, an element ''m'' not related by ''s R m'' (for instance, "''s'' is not smaller than ''m''") for any ''s'' ∈ ''S''. In other words, a relation is well founded if :(\forall S \subseteq X)\; \neq \emptyset \implies (\exists m \in S) (\forall s \in S) \lnot(s \mathrel m) Some authors include an extra condition that ''R'' is set-like, i.e., that the elements less than any given element form a set. Equivalently, assuming the axiom of dependent choice, a relation is well-founded when it contains no infinite descending chains, which can be proved when there is no infinite sequence ''x''0, ''x''1, ''x''2, ... of elements of ''X'' such that ''x''''n''+1 ''R'' ''x''n for every natural number ''n''. In order theory, a partial order is called well-founded ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Topology
In mathematics, topology (from the Greek language, Greek words , and ) is concerned with the properties of a mathematical object, geometric object that are preserved under Continuous function, continuous Deformation theory, deformations, such as Stretch factor, stretching, Twist (mathematics), twisting, crumpling, and bending; that is, without closing holes, opening holes, tearing, gluing, or passing through itself. A topological space is a set (mathematics), set endowed with a structure, called a ''Topology (structure), topology'', which allows defining continuous deformation of subspaces, and, more generally, all kinds of continuity (mathematics), continuity. Euclidean spaces, and, more generally, metric spaces are examples of a topological space, as any distance or metric defines a topology. The deformations that are considered in topology are homeomorphisms and homotopy, homotopies. A property that is invariant under such deformations is a topological property. Basic exampl ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Partial Order
In mathematics, especially order theory, a partially ordered set (also poset) formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation indicating that, for certain pairs of elements in the set, one of the elements precedes the other in the ordering. The relation itself is called a "partial order." The word ''partial'' in the names "partial order" and "partially ordered set" is used as an indication that not every pair of elements needs to be comparable. That is, there may be pairs of elements for which neither element precedes the other in the poset. Partial orders thus generalize total orders, in which every pair is comparable. Informal definition A partial order defines a notion of comparison. Two elements ''x'' and ''y'' may stand in any of four mutually exclusive relationships to each other: either ''x'' ''y'', or ''x'' and ''y'' are ''incompar ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Aczel's Anti-foundation Axiom
In the foundations of mathematics, Aczel's anti-foundation axiom is an axiom set forth by , as an alternative to the axiom of foundation in Zermelo–Fraenkel set theory. It states that every accessible pointed directed graph corresponds to exactly one set. In particular, according to this axiom, the graph consisting of a single vertex with a loop corresponds to a set that contains only itself as element, i.e. a Quine atom. A set theory obeying this axiom is necessarily a non-well-founded set theory. Accessible pointed graphs An accessible pointed graph is a directed graph with a distinguished vertex (the "root") such that for any node in the graph there is at least one path in the directed graph from the root to that node. The anti-foundation axiom postulates that each such directed graph corresponds to the membership structure of exactly one set. For example, the directed graph with only one node and an edge from that node to itself corresponds to a set of the form ''x'' = . ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Peter Aczel
Peter Henry George Aczel (; born 31 October 1941) is a British mathematician, logician and Emeritus joint Professor in the Department of Computer Science and the School of Mathematics at the University of Manchester. He is known for his work in non-well-founded set theory, constructive set theory, and Frege structures. Education Aczel completed his Bachelor of Arts in Mathematics in 1963 followed by a DPhil at the University of Oxford in 1966 under the supervision of John Crossley. Career and research After two years of visiting positions at the University of Wisconsin–Madison and Rutgers University Aczel took a position at the University of Manchester. He has also held visiting positions at the University of Oslo, California Institute of Technology, Utrecht University, Stanford University and Indiana University Bloomington. He was a visiting scholar at the Institute for Advanced Study in 2012. Aczel is on the editorial board of the ''Notre Dame Journal of Formal Logic'' and ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
John Barwise
Kenneth Jon Barwise (; June 29, 1942 – March 5, 2000) was an American mathematician, philosopher and logician who proposed some fundamental revisions to the way that logic is understood and used. Education and career Born in Independence, Missouri to Kenneth T. and Evelyn Barwise, Jon was a precocious child. A pupil of Solomon Feferman at Stanford University, Barwise started his research in infinitary logic. After positions as assistant professor at Yale University and the University of Wisconsin, during which time his interests turned to natural language, he returned to Stanford in 1983 to direct the Center for the Study of Language and Information. He began teaching at Indiana University in 1990. He was elected a Fellow of the American Academy of Arts and Sciences in 1999. In his last year, Barwise was invited to give the 2000 Gödel Lecture; he died prior to the lecture. Philosophical and logical work Barwise contended that, by being explicit about the context in whic ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Steve Awodey
Steven M. Awodey (; born 1959) is an American mathematician and logician. He is a Professor of Philosophy and Mathematics at Carnegie Mellon University. Biography Awodey studied mathematics and philosophy at the University of Marburg and the University of Chicago. He earned his Ph.D. from Chicago under Saunders Mac Lane in 1997. He is an active researcher in the areas of category theory and logic, and has also written on the philosophy of mathematics. He is one of the originators of the field of homotopy type theory. He was a member of the School of Mathematics at the Institute for Advanced Study The Institute for Advanced Study (IAS), located in Princeton, New Jersey, in the United States, is an independent center for theoretical research and intellectual inquiry. It has served as the academic home of internationally preeminent scholar ... in 2012–13. Bibliography * * References External links * * * * * {{DEFAULTSORT:Awodey, Steve American logicians 20th-cen ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |