|
N = 1 Fallacy
Pseudoreplication (sometimes unit of analysis error) has many definitions. Pseudoreplication was originally defined in 1984 by Stuart H. Hurlbert as the use of inferential statistics to test for treatment effects with data from experiments where either treatments are not replicated (though samples may be) or replicates are not statistically independent. Subsequently, Millar and Anderson identified it as a special case of inadequate specification of random factors where both random and fixed factors are present. It is sometimes narrowly interpreted as an inflation of the number of samples or replicates which are not statistically independent. This definition omits the confounding of unit and treatment effects in a misspecified F-ratio. In practice, incorrect F-ratios for statistical tests of fixed effects often arise from a default F-ratio that is formed over the error rather the mixed term. Lazic defined pseudoreplication as a problem of correlated samples where correlation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Stuart H
Stuart may refer to: Names *Stuart (name), a given name and surname (and list of people with the name) Automobile *Stuart (automobile) Places Australia Generally *Stuart Highway, connecting South Australia and the Northern Territory Northern Territory *Stuart, the former name for Alice Springs (changed 1933) * Stuart Park, an inner city suburb of Darwin *Central Mount Stuart, a mountain peak Queensland *Stuart, Queensland, a suburb of Townsville *Mount Stuart, Queensland, a suburb of Townsville *Mount Stuart (Queensland), a mountain South Australia *Stuart, South Australia, a locality in the Mid Murray Council *Electoral district of Stuart, a state electoral district *Hundred of Stuart, a cadastral unit Canada *Stuart Channel, a strait in the Gulf of Georgia region of British Columbia United Kingdom *Castle Stuart United States *Stuart, Florida *Stuart, Iowa *Stuart, Nebraska *Stuart, Oklahoma *Stuart, Virginia *Stuart Township, Holt County, Nebraska *Stu ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-ratio
F-ratio or f-ratio may refer to: * The F-ratio used in statistics, which relates the variances of independent samples; see F-distribution * f-ratio (oceanography), which relates recycled and total primary production in the surface ocean * f-number In optics, the f-number of an optical system such as a camera lens is the ratio of the system's focal length to the diameter of the entrance pupil ("clear aperture").Smith, Warren ''Modern Optical Engineering'', 4th Ed., 2007 McGraw-Hill Pro ..., f-ratio, or focal ratio, the ratio of the focal length of an optical system to the diameter of its entrance pupil See also * F-number (other) {{disambig ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Markov Chain Central Limit Theorem
In the mathematical theory of random processes, the Markov chain central limit theorem has a conclusion somewhat similar in form to that of the classic central limit theorem (CLT) of probability theory, but the quantity in the role taken by the variance in the classic CLT has a more complicated definition. See also the general form of Bienaymé's identity. Statement Suppose that: * the sequence X_1,X_2,X_3,\ldots of random elements of some set is a Markov chain that has a stationary probability distribution; and * the initial distribution of the process, i.e. the distribution of X_1, is the stationary distribution, so that X_1,X_2,X_3,\ldots are identically distributed. In the classic central limit theorem these random variables would be assumed to be independent, but here we have only the weaker assumption that the process has the Markov property; and * g is some (measurable) real-valued function for which \operatorname(g(X_1)) <+\infty. Now let : |
Pseudoreplication Correlation
Pseudoreplication (sometimes unit of analysis error) has many definitions. Pseudoreplication was originally defined in 1984 by Stuart H. Hurlbert as the use of inferential statistics to test for treatment effects with data from experiments where either treatments are not replicated (though samples may be) or replicates are not statistically independent. Subsequently, Millar and Anderson identified it as a special case of inadequate specification of random factors where both random and fixed factors are present. It is sometimes narrowly interpreted as an inflation of the number of samples or replicates which are not statistically independent. This definition omits the confounding of unit and treatment effects in a misspecified F-ratio. In practice, incorrect F-ratios for statistical tests of fixed effects often arise from a default F-ratio that is formed over the error rather the mixed term. Lazic defined pseudoreplication as a problem of correlated samples where correlation is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
F-ratio (statistics)
In probability theory and statistics, the ''F''-distribution or F-ratio, also known as Snedecor's ''F'' distribution or the Fisher–Snedecor distribution (after Ronald Fisher and George W. Snedecor) is a continuous probability distribution that arises frequently as the null distribution of a test statistic, most notably in the analysis of variance (ANOVA) and other ''F''-tests. Definition The F-distribution with ''d''1 and ''d''2 degrees of freedom is the distribution of : X = \frac where S_1 and S_2 are independent random variables with chi-square distributions with respective degrees of freedom d_1 and d_2. It can be shown to follow that the probability density function (pdf) for ''X'' is given by : \begin f(x; d_1,d_2) &= \frac \\ pt&=\frac \left(\frac\right)^ x^ \left(1+\frac \, x \right)^ \end for real ''x'' > 0. Here \mathrm is the beta function. In many applications, the parameters ''d''1 and ''d''2 are positive integers, but the distribution is ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
ANOVA
Analysis of variance (ANOVA) is a collection of statistical models and their associated estimation procedures (such as the "variation" among and between groups) used to analyze the differences among means. ANOVA was developed by the statistician Ronald Fisher. ANOVA is based on the law of total variance, where the observed variance in a particular variable is partitioned into components attributable to different sources of variation. In its simplest form, ANOVA provides a statistical test of whether two or more population means are equal, and therefore generalizes the ''t''-test beyond two means. In other words, the ANOVA is used to test the difference between two or more means. History While the analysis of variance reached fruition in the 20th century, antecedents extend centuries into the past according to Stigler. These include hypothesis testing, the partitioning of sums of squares, experimental techniques and the additive model. Laplace was performing hypothesis testing i ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Confounding
In statistics, a confounder (also confounding variable, confounding factor, extraneous determinant or lurking variable) is a variable that influences both the dependent variable and independent variable, causing a spurious association. Confounding is a causal concept, and as such, cannot be described in terms of correlations or associations.Pearl, J., (2009). Simpson's Paradox, Confounding, and Collapsibility In ''Causality: Models, Reasoning and Inference'' (2nd ed.). New York : Cambridge University Press. The existence of confounders is an important quantitative explanation why correlation does not imply causation. Confounds are threats to internal validity. Definition Confounding is defined in terms of the data generating model. Let ''X'' be some independent variable, and ''Y'' some dependent variable. To estimate the effect of ''X'' on ''Y'', the statistician must suppress the effects of extraneous variables that influence both ''X'' and ''Y''. We say that ''X'' ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Unit
In statistics, a unit is one member of a set of entities being studied. It is the main source for the mathematical abstraction of a "random variable". Common examples of a unit would be a single person, animal, plant, manufactured item, or country that belongs to a larger collection of such entities being studied. Experimental and sampling units Units are often referred to as being either experimental units, sampling units or units of observation: * An "experimental unit" is typically thought of as one member of a set of objects that are initially equal, with each object then subjected to one of several experimental treatments. Put simply, it is the smallest entity to which a treatment is applied. * A "sampling unit" is typically thought of as an object that has been sampled from a statistical population. This term is commonly used in opinion polling and survey sampling. For example, in an experiment on educational methods, methods may be applied to classrooms of students. This w ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Replication (statistics)
In engineering, science, and statistics, replication is the repetition of an experimental condition so that the variability associated with the phenomenon can be estimated. ASTM, in standard E1847, defines replication as "... the repetition of the set of all the treatment combinations to be compared in an experiment. Each of the repetitions is called a ''replicate''." Replication is not the same as repeated measurements of the same item: they are dealt with differently in statistical experimental design and data analysis. For proper sampling, a process or batch of products should be in reasonable statistical control; inherent random variation is present but variation due to assignable (special) causes is not. Evaluation or testing of a single item does not allow for item-to-item variation and may not represent the batch or process. Replication is needed to account for this variation among items and treatments. Example As an example, consider a continuous process which produces ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Statistical Hypothesis Testing
A statistical hypothesis test is a method of statistical inference used to decide whether the data at hand sufficiently support a particular hypothesis. Hypothesis testing allows us to make probabilistic statements about population parameters. History Early use While hypothesis testing was popularized early in the 20th century, early forms were used in the 1700s. The first use is credited to John Arbuthnot (1710), followed by Pierre-Simon Laplace (1770s), in analyzing the human sex ratio at birth; see . Modern origins and early controversy Modern significance testing is largely the product of Karl Pearson ( ''p''-value, Pearson's chi-squared test), William Sealy Gosset ( Student's t-distribution), and Ronald Fisher ("null hypothesis", analysis of variance, "significance test"), while hypothesis testing was developed by Jerzy Neyman and Egon Pearson (son of Karl). Ronald Fisher began his life in statistics as a Bayesian (Zabell 1992), but Fisher soon grew disenchanted with t ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
Student's T-test
A ''t''-test is any statistical hypothesis test in which the test statistic follows a Student's ''t''-distribution under the null hypothesis. It is most commonly applied when the test statistic would follow a normal distribution if the value of a Scale parameter, scaling term in the test statistic were known (typically, the scaling term is unknown and therefore a nuisance parameter). When the scaling term is estimated based on the data, the test statistic—under certain conditions—follows a Student's ''t'' distribution. The ''t''-test's most common application is to test whether the means of two populations are different. History The term "''t''-statistic" is abbreviated from "hypothesis test statistic". In statistics, the t-distribution was first derived as a Posterior probability, posterior distribution in 1876 by Friedrich Robert Helmert, Helmert and Jacob Lüroth, Lüroth. The t-distribution also appeared in a more general form as Pearson Type Pearson distribution, IV di ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
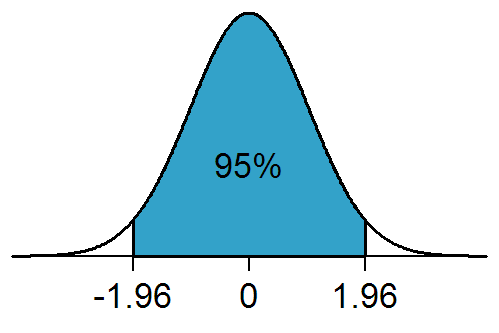
Statistical Significance
In statistical hypothesis testing, a result has statistical significance when it is very unlikely to have occurred given the null hypothesis (simply by chance alone). More precisely, a study's defined significance level, denoted by \alpha, is the probability of the study rejecting the null hypothesis, given that the null hypothesis is true; and the ''p''-value of a result, ''p'', is the probability of obtaining a result at least as extreme, given that the null hypothesis is true. The result is statistically significant, by the standards of the study, when p \le \alpha. The significance level for a study is chosen before data collection, and is typically set to 5% or much lower—depending on the field of study. In any experiment or observation that involves drawing a sample from a population, there is always the possibility that an observed effect would have occurred due to sampling error alone. But if the ''p''-value of an observed effect is less than (or equal to) the significanc ... [...More Info...] [...Related Items...] OR: [Wikipedia] [Google] [Baidu] |
